淮河流域近70年极端水文气象特征分析
2020-06-22陈素洁郝振纯王乐扬徐海卿
陈素洁,鞠 琴,郝振纯,王乐扬,徐海卿
(1.河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;2.河海大学 全球变化与水循环国际合作联合实验室,江苏 南京 210098;3.南京信息工程大学 地理科学学院,江苏 南京 210044;4.中国水利水电科学研究院,北京 100038)
根据IPCC评估报告预测,本世纪温室气体的持续排放将导致全球部分地区的暴雨、高温、干旱等极端气象水文事件进一步加剧[1],人类的生存环境及社会经济发展将面临更大挑战[2-3]。淮河流域位于东经111°55′—121°25′,北纬30°55′—36°36′,是南北地理分界线及气候过渡带,该流域气候复杂多变,导致旱涝频繁且转变急剧无常,流域的气候问题及带来的极端水文现象引起了众多学者的广泛关注:如杨赤等[4]分析了淮河流域水文极值对气候变化的响应,卢燕宇等[5]分析研究了淮河流域降水的时空演变特征,王景才等[6]分析了淮河上中游流域的年降水和主汛期降水的统计特征,田立鑫等[7]分析了淮河流域时空变化特征及年均气温和PDO的周期特征。然而结合径流分析淮河流域降水和干旱变化特征的研究较少,本文对淮河流域近70年来的降水和干旱变化特征及其径流响应进行了研究,预测了极端气象水文事件的未来趋势,其结果可为淮河流域防灾减灾及水资源管理规划工作提供数据支持。
1 研究资料和方法
1.1 研究数据
本文结合淮河流域23个气象站点1951—2016年的逐日降雨数据及淮河干流重要控制站蚌埠站的逐日径流数据,选取六个降水指数[8]和降水百分率距平分别对淮河流域的降水和干旱变化进行分析,并结合径流变化进一步揭示降水、干旱与径流之间的相关关系。极端降水指数定义见表1,干旱等级判定以《GB/T 20481—2017气象干旱等级》为准,见表2。
如图1所示,气象站点在淮河流域空间分布较均匀,因此将23个站点逐日降水数据的算数平均值作为流域面平均雨量。蚌埠站作为淮河中游主要控制站,为国家一类重点水文站,控制面积为12.13万km2,其测验数据对淮河流域的径流特征有一定的代表性[9-11]。
1.2 研究方法
1.2.1 滑动平均法
利用滑动平均法[12]和线性趋势法对降水指数序列进行初步分析,降水指数滑动平均系列为:
(1)
式中:k为滑动长度,Xj+i-1为第j+i-1年的降水指数。
1.2.2 Mann-Kendall突变检验
利用Mann-Kendall检验法[13]对降水序列进行突变检验。对于降水序列X={X1,X2…,Xn}(含有n个样本),构造一个秩序列:
(2)
式中:若Xi>Xj(j=1,2……,i),ri=1;否则ri=0,秩序列Sk是第i个时刻数值大于第j个时刻时数值个数的累加,在时间序列为随机的假设下,定义统计量:

表1 极端降水评价指数表
图1 淮河流域气象站点图示Fig.1 Meteorological station distribution in the HRB
(3)
(4)
(5)
式中:UF1=0,E(Sk)和varE(Sk)分别是Sk的均值和方差,且X1、X2……Xn互相独立时,它们具有相同连续分布。按时间序列X的逆序重复上述过程,得到另外一条曲线UBk,本文给定显著性水平α=0.05,那么临界值μ0.05=±1.96。将UFk和UBk及两条临界线绘在一张图上,若UFk和UBk两条曲线超过临界线,表明上升或下降趋势显著,超过临界线的范围为出现突变的时间区域,若UFk和UBk出现交点且交点在临界线之间,那么交点对应的时刻便是突变开始的时间。
1.2.3R/S分析法
基于R/S分析法得到的Hurst指数是定量描述时间序列信息长期依赖性的有效方法,用于判断未来趋势相对于过去趋势的变异程度,其基本原理是将一个时间序列均分为若干个数组,在每个数组内对其极值进行标准化,设数组时间长度为N,将N作为解释变量,ln[R/S]为被解释变量进行线性回归,得到线性回归方程的斜率即为Hurst指数,Hurst指数意义如表3,计算公式为[14]:
ln[R/S]=Hlna+HlnN
(6)
式中:R为极值,S为标准值,H为Hurst指数;N为时间步长。
通过统计量V可以判断出序列是否有非周期循环,且测定出周期长度,若V-ln(n)曲线由上升趋势突然转变为平稳趋势或下降趋势,则认为过去趋势对于未来趋势的影响消失,统计量V计算公式如下:
(7)

表3 Hurst指数分类表
2 结果分析
2.1 降水指数变化
2.1.1 降水趋势分析
以23个站点逐日降水的算数平均值作为淮河流域逐日面平均雨量,基于流域面雨量分析极端降水指数的年际变化,结果如图2所示,六个降水指数均呈增长趋势,其中多年平均RX1day值为39.24 mm,线性增长倾向率为1.8 mm/10 a,多年相差最大为60.64 mm,最大RX1day年份主要集中在20世纪60年代,这与余敦先等研究表明1960—2009年淮河流域最大日降水事件发生年份大多集中在20世纪60—70年代结论一致[15];多年平均SDⅡ值为7.02 mm/d,线性增长倾向率为0.225 mm/(d·10 a);多年平均R20值为7.62 d,线性增长倾向率为0.74 d/10 a;年连续湿日(CWD)为11.47 d,线性增长倾向率为0.356 d/10 a;年强降水量(R95P)为384.43 mm,线性增长倾向率为23.5 mm/10 a;多年平均降水量(PRCPTOT)为807.6 mm,线性增长倾向率为34.82 mm/10 a,降水量最多年份为2003年,降水量为1227.25 mm,降水量最少年份为1951年,降水量为103.89 mm。除连续湿日指数外,所有降水指数均通过95%置信度的显著检验(表4),说明淮河流域极端降水情况越来越严重。
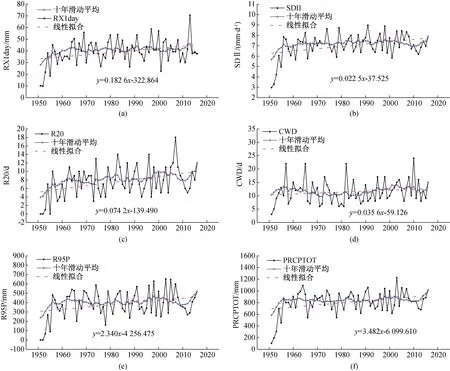
图2 极端降水指数变化趋势Fig.2 Variation trend of extreme precipitation index
2.1.2 降水突变分析
结合滑动平均以及MK突变检验结果分析(图3):RX1day和 SDⅡ均在1953年前后呈现明显的增加趋势且一直持续至今;由图3(c)可知大雨日数UF值在1951年后一直大于0,即R20一直呈现增加趋势,1962年前后R20出现均值突变,其UF值超过5%临界线,增加趋势变得显著,在1975年前后其增加趋势减缓,此后一直在临界线上下徘徊;CWD从1951年到20世纪70年代后期呈增加趋势,20世纪80年代初期到21世纪初期呈减小趋势,其后逐渐回升,整体变化趋势不明显;R95P和PRCPTOT均在1953年前后呈现明显增加趋势,但分别在1977年和1994年左右增加趋势减缓,此后一直在临界线上下波动。
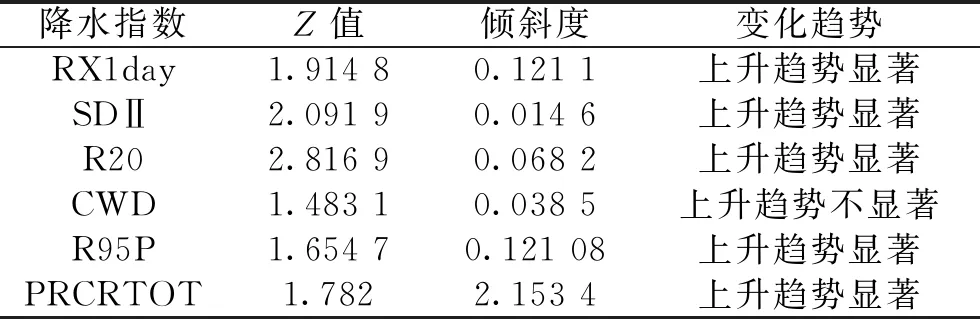
表4 极端降水指数变化趋势显著性检验结果
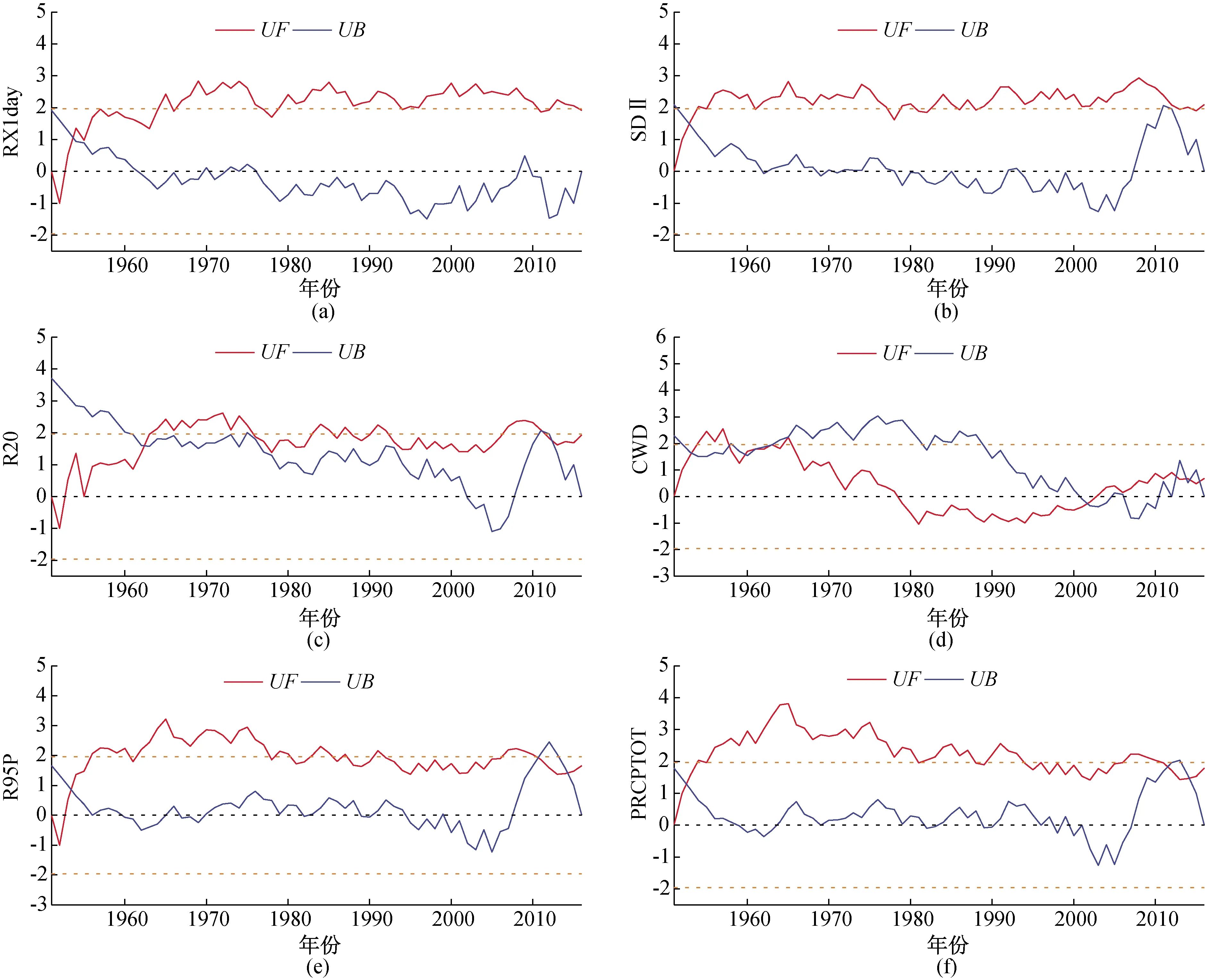
图3 极端降水指数突变检验Fig.3 Extreme precipitation index mutation test
2.2 干旱统计分析
基于流域逐日面平均雨量分别计算淮河流域年、季降水百分率距平,对淮河流域的干旱情况进行分析,特旱、重旱、中旱、轻旱和无旱分别用4、3、2、1和0代替。
从年尺度来看(图4(a)),近70年里轻旱及以上强度干旱的频率为21.2%,可见淮河流域易发生干旱灾害。由图5可知干旱年主要集中在20世纪50年代初中期、70—80年代后期以及20世纪的末期,其中1951—1955年中有4年为重旱、特旱年,1966年和1978年为中旱年,其余年份均为轻旱年。进入20世纪80年代以来,所有年份均属于轻度干旱及无旱。从年降水百分率距平来看,年降水百分率距平逐渐增加且通过了95%置信度的趋势显著性检验,可知淮河流域的干旱趋势逐渐降低。
季尺度上(图4(b)),四季无旱比例均最高,其次是轻旱、中旱、重旱和特旱;四季干旱频率分别为24.24%、16.67%、30.3%、33.33%,可见冬旱最为严重。从表5可知,近70年来,冬季发生中旱及以上强度的干旱共15次,主要集中在20世纪50年代和80年代,其中中旱年占比最高;夏季在1953年之后便没有发生过轻旱以上强度的干旱;春、秋两季干旱主要发生在21世纪的初期和20世纪的末期。四季降水量距平百分率正逐年增大(图6),线性增长速率由大到小依次为冬季、秋季、夏季、春季,可见冬季旱灾比例虽高,但其降水量距平百分率增率最大,因而冬旱频率有减小趋势。
2.3 降水、干旱对径流的响应
2.3.1 降水与径流的相关性及长程分析
结合MK趋势检验,分析年连续30天、15天最大降水和径流的趋势变化及相关性(下文均简化为最大30天降水、径流),采用R/S分析法检测最大30天降水、径流系列的未来趋势并进一步判断未来趋势持续时间。
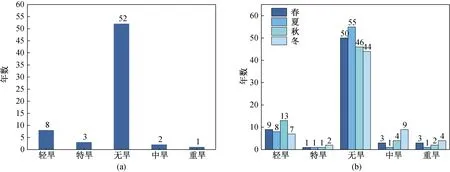
图4 1951—2016年、季干旱等级统计图Fig.4 The statistical graph of drought grade in seasons and years during 1951—2016
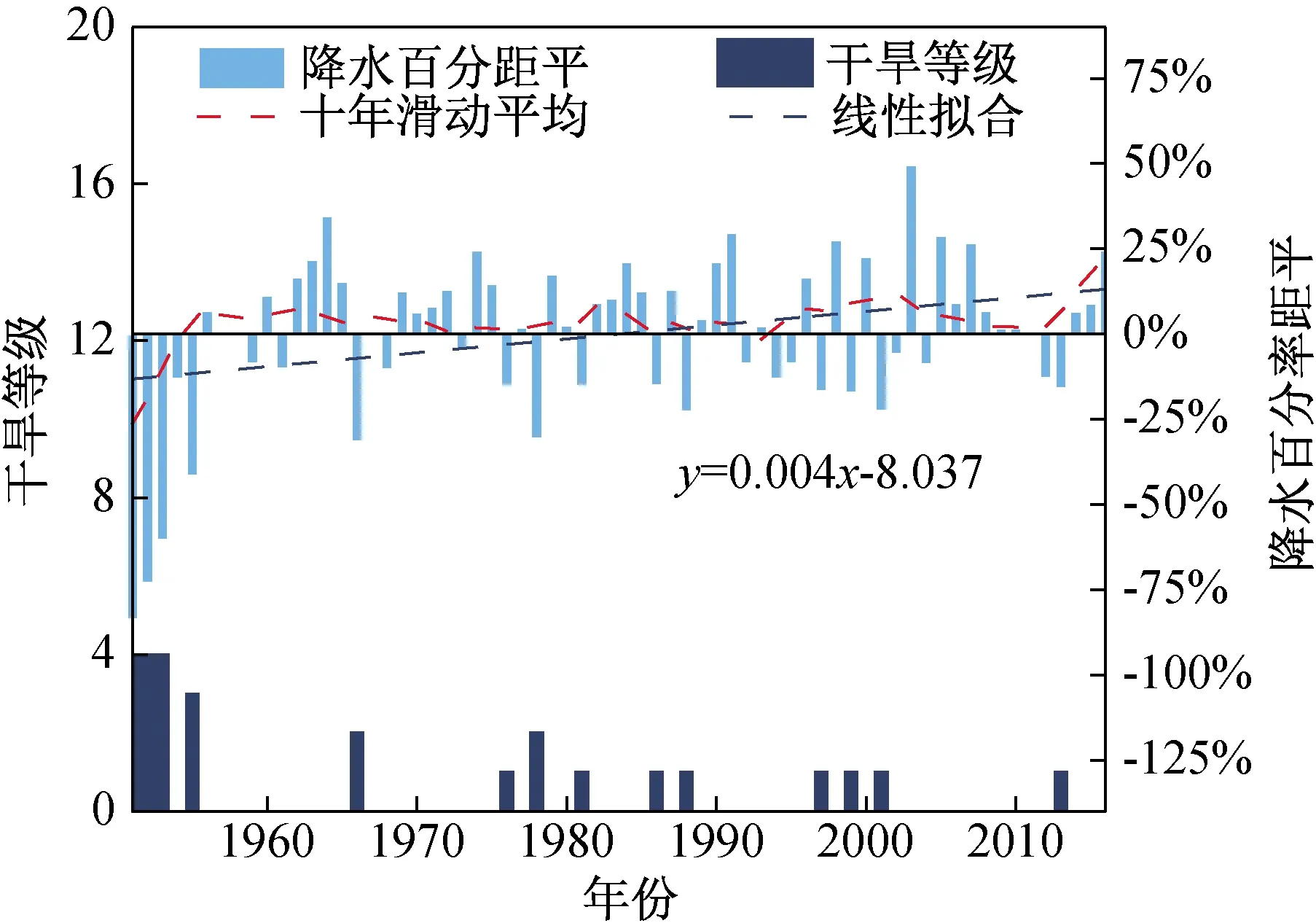
图5 年降水量距平百分率及干旱情况Fig.5 Annual precipitation anomalytrend and drought statistics
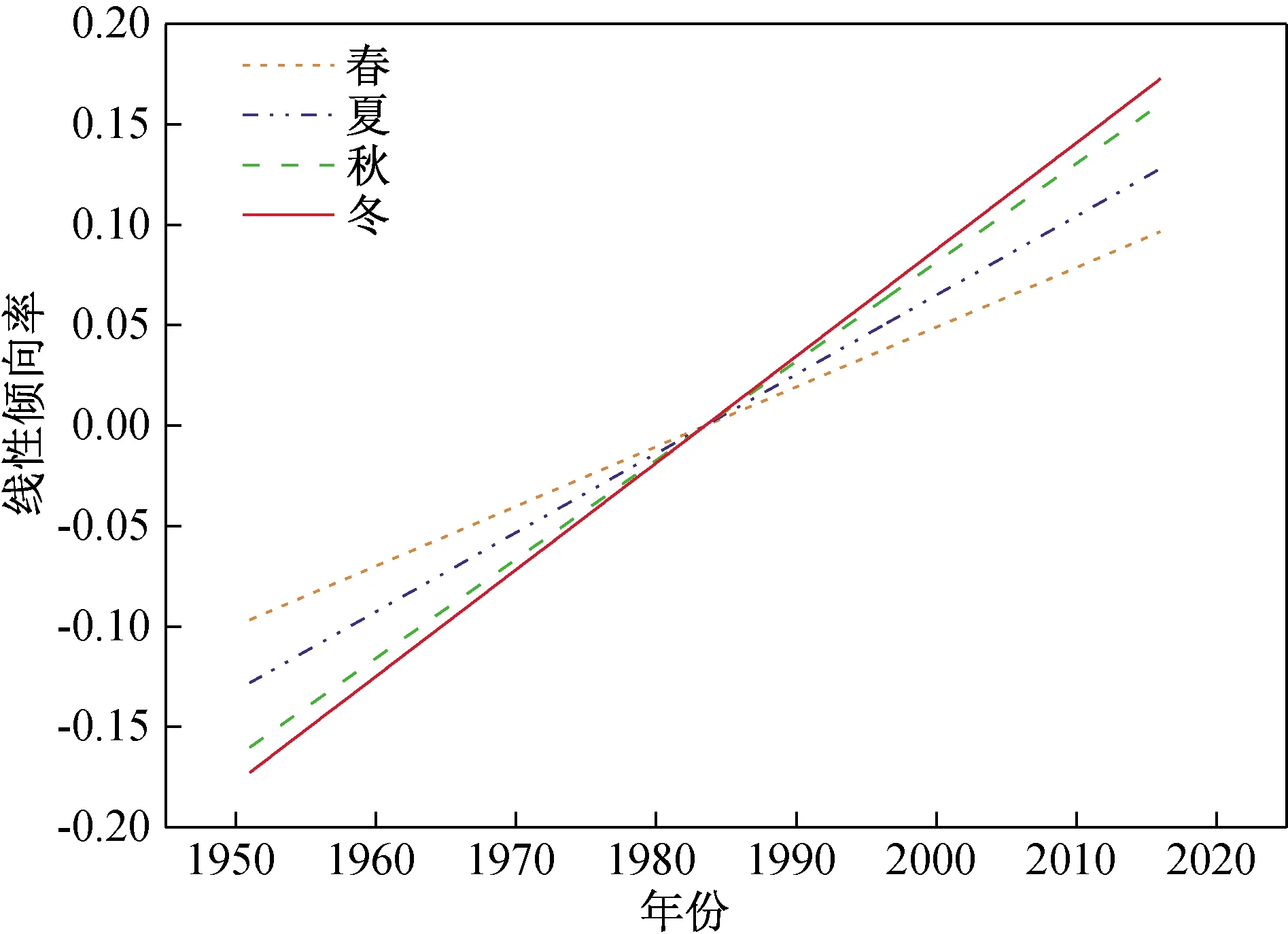
图6 季降水量距平百分率线性拟合Fig.6 Linear fitting of seasonal precipitation anomaly percentage

表5 干旱等级计算结果(季)
最大30天、15天降水均呈不显著增长趋势(图7),线性增长倾向率分别为8 mm/10 a和4.9 mm/10 a,最大30天、15天径流均呈不显著减小趋势,线性减少倾向率分别为2.97亿m3/10 a和1.39亿m3/10 a,两者变化趋势不完全一致,说明流域径流除了受到气候影响外,下垫面因素和人为影响也较大。最大30天降水Hurst指数为0.641 7,呈正弱持续性变化,从V统计量可知第一个拐点在ln(N)=2.4,即过去趋势对未来的有效影响时间长度N约为11年;同理最大30天径流Hurst指数为0.468 7,呈反弱持续性变化,持续性时间约为7年。
最大30天、15天降水与径流序列在0.01的显著水平下均呈中度相关(表6),最大30天的降水径流相关系数稍偏大一点。

表6 降水径流相关系数表
注:**在0.01水平相关性显著。
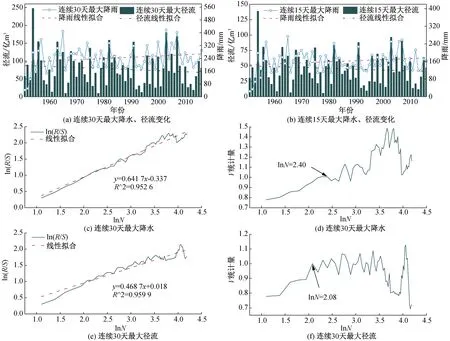
图7 最大30天、15天降水和径流趋势(a、b)及R/S分析结果图Fig.7 Maximum 30-day, 15-day precipitation and runoff trend and R / S analysis results
2.3.2 干旱与径流的相关性及长程分析
以夏季(6—8月)和冬季(12—2月)作为径流汛期和非汛期,分别分析夏、冬季降水百分率距平与径流的趋势变化、相关性和长程变异情况。因本文选取降水百分率距平作为干旱指标,所以干旱与径流的相关性分析主要以降水百分率距平与径流的相关性为主。
如图8所示,夏、冬季降水百分率距平均呈不显著增长趋势,线性增长倾向率分别为0.03 mm/10 a和0.05 mm/10 a,汛期、非汛期径流分别呈不显著减小趋势和不显著增加趋势,线性倾向率分别为6.23亿m3/10 a和0.45亿m3/10 a。夏、冬季降水百分距平序列Hurst指数分别为0.654 7和0.607 1,分别呈正强持续性变化和正弱持续性变化,从V统计量可知(表7),夏、冬季降水百分距平变化趋势可分别持续约10年和6年;汛期径流Hurst指数为0.481 4,呈反弱持续性变化,持续性时间约为4年,非汛期径流Hurst指数为0.510 6,呈正弱持续性变化,持续性时间约为8年。
通过相关性分析可知(表8),汛期降水距平与径流呈中度相关,而非汛期的降水距平与径流相关性大大降低,说明夏季降水距平对径流的影响更大,此时,径流量能较真实地反映干旱是否发生及发生干旱的强度。

表7 V统计量-时间长度统计表
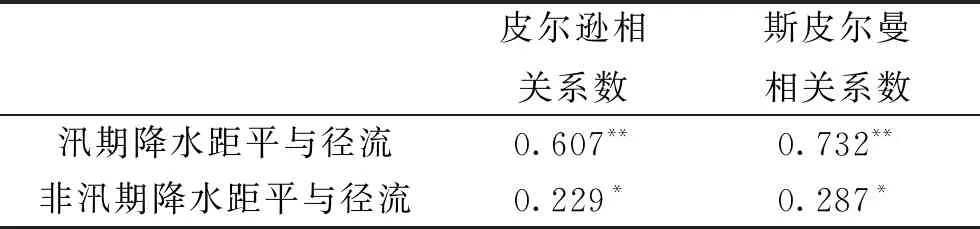
表8 降水百分距平与径流相关系数表
注:**在0.01水平相关性显著,*在0.05水平相关性显著。
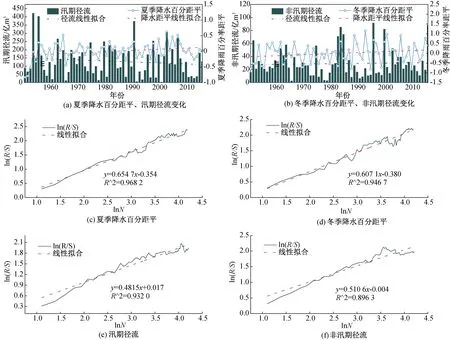
图8 汛期、非汛期降水距平和径流趋势及R/S分析结果图Fig.8 Precipitation distance and runoff trend in non-flood season and R /S analysis results
3 结论
1)六个降水指数除了CWD外,RX1day、SDⅡ、R95P、R20和PCRPTOT均呈显著增长趋势且突变年份主要集中在20世纪50年代和60年代初期。
2)近70年淮河流域干旱频率为21.2%,以轻度干旱居多,干旱年主要集中在20世纪50年代、70—80年代后期以及20世纪末期;四季冬旱最严重,夏旱最少,年、季降水距平百分率均逐年增大,建议有关部门可针对轻旱及冬旱加以预防与治理。
3) 最大30天、15天降水和径流均呈中度相关,其中,最大30天降水、径流将呈不显著增加趋势分别约11年及7年。汛期、非汛期的降水距平和径流分别呈中度相关和弱相关,且均为不显著增长趋势,该趋势降水距平将分别持续10年(汛期)和6年(非汛期),径流则分别持续4年(汛期)和8年(非汛期)。
本文虽然研究了淮河流域的气候变化及其径流响应,但是干旱分析中只采用了降水百分率距平这一种干旱指数,分析并不全面。在径流对气候变化的响应分析里,并未考虑蒸发因素,且径流数据只选取了蚌埠水文站一个站点的数据,以上问题是本次研究的不足点,将在下一步工作中进行深入研究。
