基于球铰应力差法的T构转体桥不平衡力矩预估分析

李 洋

（中铁四局集团第二工程有限公司，江苏 苏州 215100）

1 T构转体桥的转动系统和平衡控制

1.1 转动系统和抗倾覆系统

大吨位的T构转体桥的转动系统和抗倾覆系统主要由混凝土上转盘和下转盘、撑脚、钢板滑道、定位钢销轴、球铰、千斤顶及千斤顶反力座组成。在转动系统和抗倾覆系统中球铰是整个系统的关键，主要作用是承担转体桥的转体重量、降低摩擦系数，从而降低转体施工时的牵引力矩值，在转体施工前要提前配置黄油和四氟乙烯混合物填至上、下球铰间的四氯乙烯滑块的间隙处，使四氯乙烯滑块与聚四氟滑板平齐。撑脚的作用是避免T构转体桥发生倾覆，是避免倾覆的最后一道防线，所以在设置时需要严格控制撑脚和环形滑道之间的缝隙。缝隙过大时，T构转体桥转体施工时易发生较大晃动，降低桥体结构的稳定性；缝隙过小时，T构转体桥转体施工时易发生撑脚和环形滑道卡死，对施工产生不利影响。

1.2 转体不平衡力矩处理方案

在桥梁段现浇筑施工完成后要进行施工支架拆除，这时转体桥处于最大悬臂状态，因此要保证转体桥的稳定性，避免造成安全隐患，转体前需要确定不平衡力矩值，然后进行桥体平衡配重，保证转体施工时桥体处于瞬态平衡状态。

当不平衡力矩值较小时，球铰和四氯乙烯滑块涂有油脂增加润滑，摩擦力较小，这时的牵引力矩值也较小，所以这种情况下不需要进行称重试验，只需要根据施工现场的具体施工情况进行配重预估（可以根据撑脚和聚四氟滑板的间隙变化为判断依据），然后直接进行桥体平衡配重。特别是施工现场风荷载较大条件下，要尽量缩短转体桥悬臂时间，尽快进行平衡配重后完成转体及封铰施工，保证桥梁的整体结构稳定。

当不平衡力矩值较大时，可以先根据施工现场的具体施工情况进行初步配重预估，然后观察撑脚和聚四氟滑板的间隙变化，再结合类似转体桥施工得到的动摩擦系数范围值，确定合适的称重试验设备仪器和位移测量仪，最终完成转体桥平衡配重，节约转体施工时间和施工成本。

2 球铰下应力差法的不平衡力矩计算公式

在T构转体桥转体施工前桥梁的自重主要依靠施工支架支撑，这时的不平衡力矩数值不会对球铰处的应力状态产生影响，所以可将这时球铰处应力状态作为初始应力状态。当桥梁段现浇筑施工完成、施工支架卸除后，球铰处应力状态发生转变，这时球铰承担不平衡力矩，会与初始应力状态产生一定数值的应力差，可以根据应力差值大小估算出相应施工条件下T构转体桥的平衡状态，确定桥体平衡配重数值。

从T构转体桥转动系统和抗倾覆系统内部构造可以看出，现浇梁施工完成整体落架后，球铰将承受来自桥梁的竖向压应力和不平衡力矩产生的作用力，球铰这时处于偏心受压状态（见图1）。

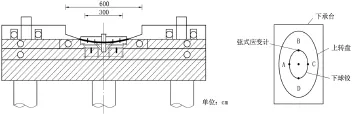
图1 球铰处传感器的具体布置示意图

根据偏心受压的应力分布特点，并参照车晓军等[1]发表的平转桥梁墩柱钢筋倒塌对转动支座受力影响分析，确定撑脚和钢板滑道接触紧密的一侧（撑脚受压侧）的应力值计算公式为：

撑脚受压侧的对侧应力值为：

撑脚两侧应力差为：

不平衡力矩的理论计算值为：

式中：N为竖向压力；M为不平衡力矩；y为应力测点到截面中性轴的距离；I为抗弯惯性矩，球铰接触面直径为d时，I值取。

实际T构转体桥施工时应力应变的测量方法通常为在转体桥的横向及纵向位置的大小桩号处分别布置2个传感器（钢弦应变传感器）（见图1），测量转体桥施工支架拆除前后球铰处应力变化值，再结合公式（4）及自平衡T构桥转体施工的有关计算，可以确定T构转体桥转动不平衡力矩沿桥梁纵向及横向的力矩值。

不平衡力矩的纵向计算值为：

不平衡力矩的横向计算值为：

式中：εZy、εHy为纵向、横向撑脚受压侧的应力变化值；εZ1、εH1为纵向、横向撑脚受压侧的对侧应力变化值。

3 不平衡力矩预估方法

通过建立有限元模型，可以求得球铰空间细部分析的竖向压力荷载（外部荷载）数值大小，并利用此值进行球铰局部模型分析。不平衡力矩在实际工程中，常根据施工经验，例如撑脚和聚四氟滑板的间隙变化为判断依据，可以预估不平衡力矩的大小范围和方向，不能具体确定不平衡力矩值，因此可以通过建立有限元模型进一步确定不平衡力矩的数值大小。具体分析方式如下：（1）按照球铰尺寸比例，建立局部分析模型，将公式（5）、公式（6）得出的不平衡力矩值代入模型中，进行外部荷载下的模型分析。（2）根据钢弦应变传感器的布置特点，对球铰空间对应部分进行加密网格划分，利用有限元模型对传感器周围的应力应变进行分析计算。（3）利用钢弦应变传感器实测的应力应变数据，将桥梁混凝土弹性模量值转化成T构转体桥实测应力值和模型计算的理论应力值进行对比。（4）假设球铰应力变化的敏感因素只有不平衡弯矩，其他因素影响非常小，根据理论计算和实际测量得出应力差，进行反推分析，在公式（5）、公式（6）的基础上，进一步获取精确不平衡力矩值，优化计算精度。

4 工程实例

4.1 工程概况

宁波市轨道交通4号线是宁波市轨道交通的主要规划干线，此轨道全长36.11km，全线预计建设地下车站18座、高架车站7座。在宁波市轨道交通4号线规划中将建设国内首例复杂刚构转体桥，该刚构转体桥为宁波市轨道交通4号线的关键控制性工程，转体桥全长301m，共分成2个T构进行悬臂施工，一侧长172m，重量15000t，另一侧长100m，重量8000t。在转体立交桥下球铰的支撑钢架处横向及纵向位置分别布置2个传感器（钢弦应变传感器）。

4.2 球铰局部有限元模型分析

该工程建立的转体立交桥球铰空间细部分析软件采用Abaqus工程模拟有限元软件进行计算分析，根据该工程使用的球铰尺寸，运用有限元C3D8I单元模拟球铰的转盘应力，对模型进行整体分析计算出桥墩处的内力值大小，当作球铰的外部荷载。

4.3 不平衡力矩预估

在支架现浇施工完成将所有支架拆除后，观察撑脚和聚四氟滑板的间隙变化情况，在转体立交桥横向位置，由于此工程所建的转体立交桥桥梁宽度不大，且施工线路是弯曲线段，桥梁两侧撑脚未和聚四氟滑板滑块接触，所以可以判定横向的不平衡力矩值比较小。在转体立交桥纵向位置，小桩号位置处的侧撑脚和聚四氟滑板滑块保有一定距离，大桩号位置处的侧撑脚和聚四氟滑板滑块接触，由此可以断定大桩号位置处的外部荷载较大，不平衡力矩偏向大桩号。根据有限元分析计算确定不平衡力矩预估数值大小，然后配重预估，确定合适的称重试验设备仪器和位移测量仪，进行称重试验。

根据钢弦应变传感器得到的施工现场实际应力应变数据，纳入上文的理论计算公式中，并进行有限元仿真进一步分析，分别得到理论计算值、有限元分析值，并和称重试验得到的不平衡力矩实测值进行对比，判断三组数值的误差大小（见表1）。

表1 不平衡力矩预估值和称重试验值对比 单位：kN·m

由表1结果可以看出，横向不平衡力矩值较小，这和上文判断一致，纵向的不平衡力矩值较大，理论计算值与有限元分析值和称重试验值对比，前两数值均偏大，偏差值分别为7.81%、10.01%，总体来说此结果和称重试验值比较接近。对存在的误差进行分析发现，导致出现误差的原因是读数误差、温度、钢弦应变传感器布置偏差等，在实际施工时注意以上因素可有效降低误差。

5 结束语

文章基于偏心受压部件的应力分布特点，推导出T构转体桥不平衡力矩的理论计算公式。为验证公式的偏差大小，根据某地区新建的转体立交桥作为工程实例，进一步进行有限元模型分析和开展称重试验，经分析证明经理论计算的预估值误差较小，在控制影响因素的前提下可以利用，可为同类型工程施工提供参考。