弹性车轮刚度与金属件结构优化研究

刘虹蔚，陆正刚，岳科宇

（同济大学铁道与城市轨道交通研究院，上海 201800）

0 引言

由于橡胶元件的存在，弹性车轮有减振降噪、减小冲击、降低磨耗的优势[1]，近年来广泛运用于低地板车辆。虽然弹性车轮优势较钢轮明显，但是在列车运行过程中车轮受力较复杂，不仅要承受车辆垂直静载荷和车辆运行产生的动载荷，还要承受垂向冲击力、制动力矩、转动力矩和横向力等，弹性车轮必须具有合适的刚度强度性能，否则，径向刚度不足致轮毂断裂，轴向刚度不足致落轨或脱轨，扭转刚度不足致制动失效和迟滞[2-3]。目前主要存在3种类型的弹性车轮:压缩型、剪切型和压剪复合型弹性车轮[4]。压缩型和剪切型的径向、轴向刚度匹配不均衡；压剪复合型主要以V型为主，可以调整V型角从而合理匹配合适的轴向径向刚度[5]，因此近几年被广泛应用。目前存在不同V型角和不同金属件截面形状结构的弹性车轮，由于压剪复合型的弹性车轮还未有设计标准，研究弹性车轮结构形状对弹性车轮的三向刚度的影响，能为弹性车轮结构优化设计提供参考。

本文主要以某有轨电车弹性车轮的形状参数为原型，以橡胶环和金属件接触区域型腔体积为不变量，探究不同截面形状结构类型的金属件对弹性车轮刚度的影响，为之后的弹性车轮设计奠定基础。目前主要有2种截面形状的压剪复合型弹性车轮，一种是金属件截面有凹槽的弹性车轮，另一种是金属件截面无凹槽的弹性车轮。如图1[6]所示。

图1 不同截面形状的压剪复合型弹性车轮

1 弹性车轮材料模型

1.1 橡胶材料模型

弹性车轮中弹性元件的材料是橡胶，是一种弹性模量小、伸长率很高的超弹性材料，它具有不可以压缩性，体积变化量很小[7]，但其形状可以任意改变，是一种具有几何非线性和材料非线性的特殊材料。

在有限元分析中，无法利用其弹性模量和泊松比来模拟它的力学性能，所以研究中一般使用多项式形式的应变能密度函数来模拟其力学性能[6-8]，即：

式中：J为弹性体积比；Cij,Di为温度相关的材料参数，分别描述了材料的剪切特性与可压缩性；Iˉ1,Iˉ2分别为材料的第一、第二变形张量不变量。

鉴于本实验已经有橡胶的单轴拉伸试验数据，故可以通过拟合的方法来得到橡胶的力学模型参数[9]。图2所示为拟合的试验数据曲线。结合图中所示的等双轴仿真曲线和单轴拉伸试验曲线，ABAQUS软件可以自动拟合出Mooney-Rivilin模型对应参数，即图中的综合拟合曲线。

图2 等双轴仿真、单轴拉伸试验和综合拟合曲线

1.2 金属材料参数

对于金属材料，所用的材料参数如表1所示。

表1 钢Von Mises屈服模型的材料参数

2 弹性车轮预压装有限元模型

本文使用以某有轨电车弹性车轮为原型，以金属件与橡胶环接触区域的型腔体积为不变量，改变金属件（轮毂、压环、轮芯）截面形状，分别用截面形状为无凹槽，凹槽半径为R2.5 mm，凹槽半径为R5 mm的弹性车轮进行刚度仿真试验，如图3（a）～（d）所示，图3（a）～（c）表示轮毂与橡胶环接触区域的截面形状，3（d）～（f）表示3种类型的弹性车轮装配图。车轮直径为600 mm，车轮主要由轮毂、轮芯、压环、橡胶环以及20个紧固螺栓组成，橡胶环与轮芯、轮毂及压环过盈配合，通过压环和轮芯从两侧挤压橡胶元件，待橡胶元件压紧后使用紧固螺栓将压环与轮芯连接。

图3 不同截面形状弹性车轮组成图

采用六面体实体单元进行部件离散化，轮毂、轮芯、压环、橡胶环都是C3D8R六面体减缩积分单元，划分单元数目分别为28 350、27 000、10 850、1 575 360，如图4所示。由于本文模拟弹性车轮压装和静刚度试验过程，并未研究实际运行工况下的轮轨接触，因此本次仿真简化了压环、轮芯、橡胶环的螺栓孔，不施加其螺栓预紧力。

图4 弹性车轮各零件网格离散图

2.1 相互作用及边界条件

由弹性车轮的压装过程[10]可知，分为2个分析步，由于轮毂与橡胶环存在初始过盈，第一步消除接触过盈，使轮毂与橡胶环充分接触；第二步固定轮芯，压环通过对橡胶环一侧施压，在压环的作用力下，橡胶带动轮毂移动到与轮芯紧密接触，直至填充满整个凹槽部分，如图5所示。

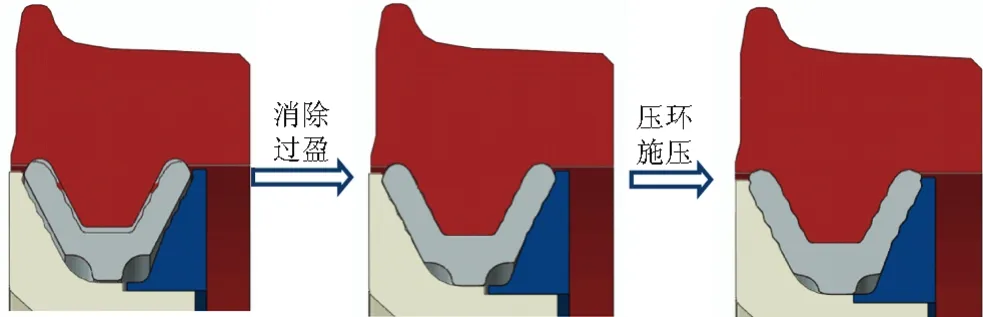
图5 有限元装配图

弹性车轮中各金属件与橡胶之间力的传递通过接触来实现。压装过程中共设3个接触对：弹性体-轮箍接触对、弹性体-轮芯接触对和弹性体-压环接触对。接触关系主要包括2个方面，即切向行为和法向行为。切向采用摩擦系数为0.2的罚函数，而在法向则采用“硬”接触。各个接触对均采用变形大、网格小的橡胶面作为从面。

图6 原型弹性车轮剖面图

图7 轮毂接触区域接触应力-距离分布图

2.2 弹性车轮压装仿真分析

以截面凹槽半径为2.5 mm的弹性车轮为例，进行压装仿真分析。

图6所示为原型弹性车轮的剖面图，金属件与橡胶接触区域主要是图示深色区域。图7～9为压装完成后，3种结构的金属件与橡胶接触面处的接触应力-距离变化图。图7可看出，中间0.5 mm左右为轮毂与橡胶接触底部平面，是压装接触应力最小的区域，整个分布走势与轮毂截面结构一致，半径R2.5 mm的轮毂接触应力最大，这和图8～9的规律类似。由图可知，压装后，接触应力在金属件凹槽区域呈现锯齿状分布，与金属件截面形状分布一致。接触应力最大值都在金属件凹槽深处，在平滑区域接触应力相对较小，凹槽越深，接触应力越大。

图8 轮芯接触区域接触应力-距离分布图

图9 压环接触区域接触应力-距离分布图

图10 ～13所示为压装完成后型腔凹槽半径为R2.5 mm的弹性车轮截面Von Mises应力分布图。可以看出：压装中最大应力分布在轮芯与橡胶过渡区域，但未超过轮芯强度极限，满足强度要求。轮箍最大应力在10.22 MPa左右，轮芯最大应力在83.63 MPa左右，橡胶环最大应力在6.889 MPa左右，压环应力在10.95 MPa左右，均满足强度要求。

图10 轮毂应力分布图

图11 橡胶环应力分布图

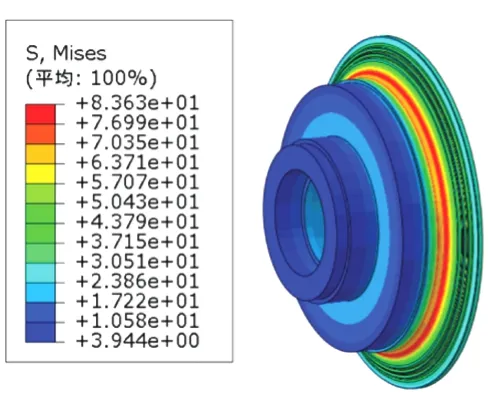
图12 轮芯应力分布图

图13 压环应力分布图

图14 为3种截面结构类型的弹性车轮按照默认压缩量压装完成后的Von Mises应力分布情况。从表中可看出，R2.5 mm的轮芯最大应力最大，在83.63 MPa左右。3种弹性车轮的压装最大应力都在轮芯与橡胶环过渡处，且各零部件的压装应力均符合强度要求。

图14 不同类型的金属件Von Mises应力分布柱状图

3 型腔截面形状对刚度的影响

以无凹槽、凹槽半径R2.5 mm、凹槽半径R5 mm的3种金属件截面结构，探究型腔截面形状对弹性车轮三向刚度的影响。在压装完成后的弹性车轮基础上，利用Abaqus/Standard进行径向刚度、轴向刚度、扭转刚度仿真分析。其中，径向刚度是施加径向载荷为108.8 kN测量得到；轴向刚度是施加径向载荷为108.8 kN，再施加61.5 kN后测量得到；扭转刚度是扭矩施加在轮箍踏面耦合的参考点上测量得到。图15为轮毂刚度加载位置示意图。

图15 轮毂加载位置示意图

3.1 不同截面结构对刚度的影响

图16 所示为弹性车轮径向载荷-位移曲线。可以从图中看出，垂向载荷与位移呈一定的线性关系，当载荷达到最大时，R5 mm的车轮径向刚度曲线最陡峭，即径向刚度最大，约为245 kN/mm，3种类型的弹性车轮径向刚度差别不大，径向刚度随着凹槽半径增大而增大，但有凹槽的比无凹槽的径向刚度稍大。

图16 弹性车轮径向载荷-位移曲线

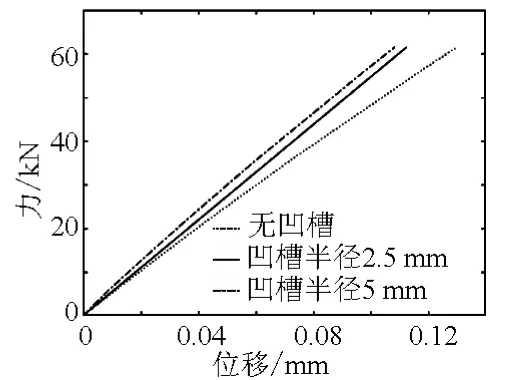
图17 弹性车轮轴向载荷-位移曲线

图17 所示为弹性车轮轴向载荷-位移曲线。可以从图中看出，轴向载荷与位移呈线性关系，与径向刚度规律大致相同，凹槽R5 mm的车轮轴向刚度最大，为567 kN/mm左右，轴向刚度随着凹槽半径增大而增大，但有凹槽的比无凹槽的刚度稍大。

图18所示为弹性车轮扭转载荷-位移曲线，图19所示为弹性车轮扭矩刚度-时间曲线。可看出，当扭矩在2～5 kN·m后，车轮开始出现打滑现象。R2.5 mm的弹性车轮的扭转刚度最大为5 119 kN·m·rad-1，与无凹槽的弹性车轮扭转刚度相差不大，凹槽R5 mm的车轮扭转刚度最小。

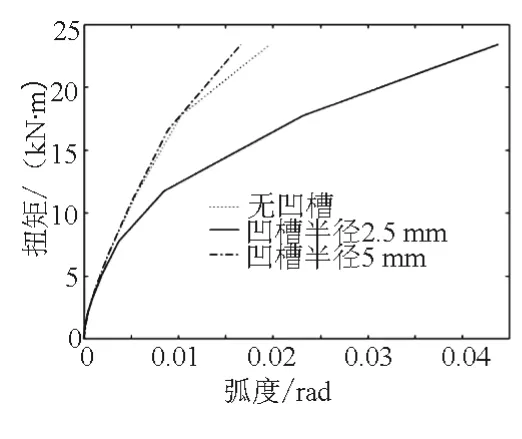
图18 弹性车轮扭矩载荷-位移曲线

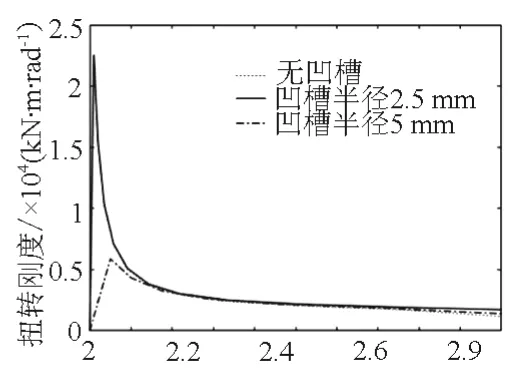
图19 弹性车轮扭矩刚度-时间曲线

图20所示为3种车轮三向刚度仿真结果对比柱状图。表明在目前的橡胶参数和预压缩量下，凹槽半径越大，径向刚度和轴向刚度更高，凹槽深的截面形状有利于提高弹性车轮的扭转刚度，但凹槽较浅反而会降低扭转刚度。

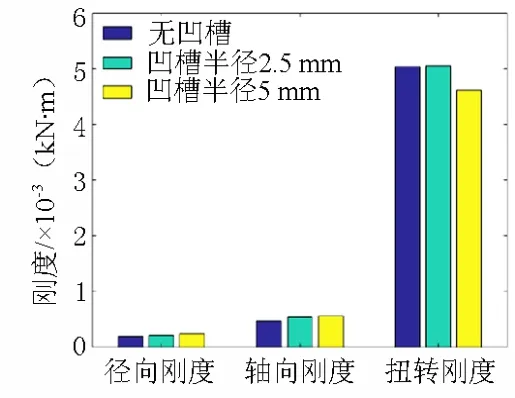
图20 3种弹性车轮三向刚度仿真结果柱状图

4 结束语

本文以某有轨电车弹性车轮为原型，通过改变金属件的截面形状，研究金属件截面结构对弹性车轮三向刚度的影响。根据上述的研究表明，弹性车轮金属件的截面结构对弹性车轮刚度有一定影响：径向刚度与轴向刚度随着凹槽半径的增大而增大，有凹槽比无凹槽的刚度值大，随着凹槽越深，扭转刚度越大，但凹槽过浅将无法提高扭转刚度，反会稍降。总而言之，适当增加弹性车轮金属件截面的凹槽能增大弹性车轮的三向刚度，且增加凹槽结构也满足强度要求。因此，本文的研究能为之后弹性车轮结构优化设计奠定基础，为弹性车轮的实车应用提供参考。