基于MATLAB的双前桥汽车钢板弹簧的刚度匹配优化

张学萍，王 娜

(安徽三联学院 机械工程学院，安徽 合肥 230601)

在整车系统设计时，若忽略悬架系统对整车制动性能的影响，在整车的平顺性和操纵稳定性方面，悬架系统是极其重要的[1-3]。悬架系统设计的实质就是将悬架与整车系统性能相匹配，匹配方式涉及悬架的结构型式及相关参数和特性参数等。过去，制造样车的方式是通过反复试验，通过类比和经验法，将测试结果与整车性能要求进行对比分析，观测悬架与整车系统是否匹配[4-6]。目前，现代设计方法以现代设计理论为基础，在机械设计、控制理论等方面得到了更为广泛的应用。现代设计方法可提高设计的效率，减少盲目性及试验压力，是一项系统工程，以性能协调、仿真分析为核心，并有机结合了设计过程中的各个环节，如结构及参数优化、系统选型、性能试验等。

由于双前桥为牵引方式的系列车型的结构形式较为新颖，因此其相关设计理论、分析方法、原则等还尚不成熟[7-9]。针对该车型的一般的设计理念是以满足整车平顺性、通过性和操纵稳定性等性能作为出发点，在集成悬架与整车相匹配的条件下，建立相关的分析技术。实现悬架与整车相匹配的优化设计。

1 整车振动模型的建立

对双前桥汽车的悬架与整车系统的匹配来说，性能协调问题是一个优化设计问题。在考虑钢板弹簧刚度时，需要构建“悬架—整车”的虚拟样机模型，根据虚拟样机模型，可建立性能协调分析的优化模型，从而实现性能协调的优化模型设计。对双前桥牵引方式的车型，假定汽车结构是左右对称的，且左、右车辙的不平度函数是相同的，因此可将其简化为一个半车模型。如图1所示，可知半车模型共有6个自由度。根据半车模型，可知对平顺性的影响最大的参数是汽车车身的垂直振动Z和俯仰振动θ。

图1 六自由度振动模型

分析对车身、三个车桥和座椅处进行受力分析，得到式(1)运动方程。

式(2)为各车桥处对应的车身位移。

(2)

2 整车振动系统频域分析

2.1 确定频域方程

系统响应分析方法主有时域分析和频域分析。时域分析需要求解微分方程或方程组。频域分析法以输入信号的频率为变量来研究系统的响应、系统结构参数与性能关系等。由于频域分析方法可方便地编制在MATLAB中使用，因此本文将采用频域分析方法。

根据图1和公式，可将公式写为矩阵形式：

(3)

式中，M—质量矩阵；C—阻尼矩阵；

K—刚度矩阵。

激励矩阵：

(4)

变量Z为：

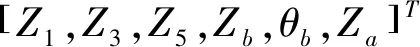
(5)

路面不平度向量Q：

Q=[Zf,Zm,Zr]T

(6)

通过傅里叶变换对转换振动微分方程，得传递函数：

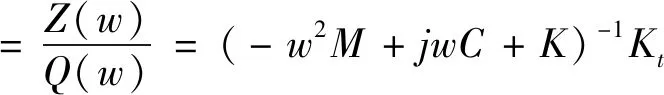
(7)

则可得系统的频率响应函数为：

(8)

根据随机振动相关理论可知在线性系统中的振动响应功率谱密度函数为：

Gx(f)=H*(f)G(f)H(f)T

(9)

式中,Gx(f)—振动响应的功率谱密度，m2·s；

H*(f)—系统频率响应函数矩阵的共轭转置；

G(f)—路面输入的功率谱密度，m2·s；

H(f)T—系统频率响应函数矩阵的转置。

2.2 三轴输入的路面输入模型

根据国家标准《车辆振动输入路面不平度表示》(GB7031—86)，可查询得到空间频率的路面谱密度拟合函数为：

(10)

时间频率功率谱密度Gq(f)可由Gq(n)转换得到：

(11)

式中,Gq(n0)—路面不平度系数，m3；

n—空间频率，m-1；

n0—参考空间频率，n0=0.1m-1；

w—频率指数，取w=2；

u—车速，m/s；f—时间频率,Hz。

一桥、二桥和后桥可以简化成平面模型，此时假设车轮沿同一路面行驶。根据相关换算，得到三轴系统相关的路面对车辆振动系统的输入谱矩阵为：

(12)

式中，L1=a-c；L2=a+b；L3=b+c。

2.3 座椅处的加权加速度均方根值

座椅处的频率响应函数为一个一行三列(1×3)矩阵，其表达式为：

(13)

将w=2πf代入公式(13)，可得座椅处的响应功率谱为：

(14)

响应的加速度响应谱为：

(15)

考虑频率加权函数，可得加速度均方根值为：

(16)

由于只考虑垂向振动，因此频率加权函数可表示为：

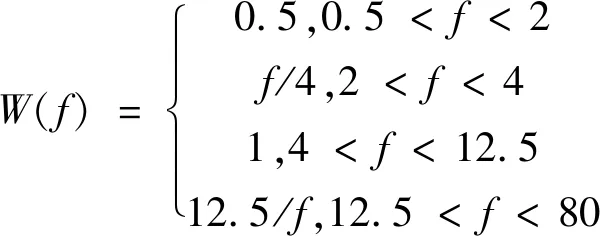
(17)

3 MATLAB程序设计

将加权加速度均方根值aw作为优化指标，在MATLAB中编制求解其最小值的优化程序，优化设计的约束条件包括：悬架偏频、偏频比、车身侧倾角、悬架动挠度，如图2所示，从而可建立悬架刚度与整车平顺性和操纵稳定性相协调的优化模型。

图2 MATLAB优化流程图

使用二次规划方法，在MATLAB优化工具箱中利用fmincon函数进行求解，从而可匹配双前桥牵引车的前钢板弹簧的刚度值。如图2所示，MATLAB优化程序主要包括主调用函数、目标函数和约束函数。设置原车一、二桥钢板弹簧刚度参数初始值分别为x0=[293 000，293 000]，即Ksf=293 000 N/m；Ksm=293 000 N/m。

(1)模型的设计变量为前、中桥悬架的刚度X=[Ksf;Ksm]。

(2)主调用函数程序

若函数头部为[x,fval]=fmincon[@myobj,x0,[],[],[],[],@confun,options]，该句程序的作用是调用目标函数，但不包括约束，如调用主调用函数为zhudiaoyong.m。

主调用函数头设计为：

function[x,fval]=zhudiaoyong

globalMaKaCaMwfMwmMwrMhbIhbCsfCsmCsrKsrKtfKtmKtrabcduL1L2L3hpmsfmsmmsrB1B2B3msa_yg

若函数头部为[x,fval]=fmincon(@myobj,x0,[],[],[],[],lb,ub,@confun,options)，该句程序包含了目标函数的约束上界和约束下界及目标函数，为有约束最优解求解函数。

(3)目标函数

加权加速度均方根值与驾驶员的驾车舒适性有重要联系，因此可选用aw作为评价指标，该指标也是评价行驶平顺性的重要指标。而在进行汽车性能设计时，钢板弹簧参数的确定取决于行驶平顺性的要求，因此可设计优化目标为aw，目标函数可设计为求解aw最小值函数：

(18)

在MATLAB中编写目标函数myobj.m：function aw6=myobj(x)

globalMaKaCaMwfMwmMwrMhbIhbCsfCsmCsrKsrKtfKtmKtrabcduL1L2L3

(4)约束条件

约束函数要满足汽车行驶平顺性和操纵稳定性相关性能的标准，因此可得相关的约束条件。

①前、后悬架的侧倾角约束

悬架刚度是整车的操纵稳定性重要影响因素，标准中以0.4 g的侧向加速度为其车身侧倾角ψ0.4，因此可得侧倾角约束条件为：

(19)

②前、后悬悬架的偏频与偏频比约束

悬架偏频是汽车具有良好平顺性的重要影响因素。因此，设前后悬架簧质量变量为msf,msm，前、后悬架的偏频f1,f2要满足在[1.5,2.2]范围内。为了减少汽车的角振动，汽车前后悬架偏频比约束条件满足的关系一般为：

(20)

③悬架动挠度约束

汽车在不平路面上行驶的时候，为了防止平顺性变坏，悬架还必须要有一定的动挠度fd，如前悬架的动挠度为fd=Z2-Z1,通常选取fd的最大值；而悬架动挠度的均方根值σfd≤[fd]/3时，可以保证悬架撞击限位块的概率小于0.3%。

根据以上约束条件，在MATLAB中编写约束函数confun.m：function[c,ceq]=confun(x)

4 优化结果分析

在MATLAB中编写好双前桥牵引车钢板弹簧刚度匹配程序[3]后，用户可以交互式输入汽车基本结构参数，经过MATLAB计算后即可获得优化计算结果，程序可输出优化前和优化后的评价性能参数值，优化结果(见表1)。

表1 优化前后钢板弹簧刚度值

通过建立“悬架—整车”系统优化模型，可揭示整车平顺性、操纵稳定性与悬架系统特征设计参数之间的定量关系。在优化设计过程中，设置一桥、二桥的钢板弹簧刚度为设计变量，以适当降低一桥、二桥板簧的刚度，提高座椅舒适性。对车身侧倾角的变化可采取措施适当补偿。表1反映了优化前后车身侧倾角的变化，优化后的车身侧倾角比优化前大0.029°，相对变化量为2.31%，而优化后的加权加速度均方根值比优化前小0.097 m/s2,相对变化量为15.05%，从图3的优化前后座椅处的加速度功率谱也可以看出加速度峰值明显下降。针对二者的相对变化量，双前桥钢板弹簧刚度值对整车平顺性的影响比较大，对整车操纵稳定性影响比较小一点。考虑提高舒适性，增强操纵稳定性，并协调二者的性能，建议可以在一桥悬架处增加横向稳定杆来减小车身侧倾角。如此，可以在提高舒适性同时，保证操纵稳定性不会降低。

图3 优化前后座椅处的加速度功率谱曲线

上述计算分析需要大量的“悬架—整车”特性参数，相关参数确定较为困难，再加上“悬架—整车”集成系统的复杂性，影响因素的多样性，整个模型分析尚需要多方检验。同时，优化模型主要是针对试验样车参数进行仿真分析的，没有考虑牵引状态下实际挂车装载，此时相关整车轴荷等参数会发生变化，因此还需要进一步分析验证。

5 结语

本论文通过建立6个自由度的半车模型，理论分析双前桥汽车前钢板弹簧刚度对整车平顺性和操纵稳定性的影响，利用MATLAB优化工具箱中的fmincon函数编写优化程序，最终得出协调整车平顺性和操纵稳定性的前钢板弹簧匹配优化结果，结果表明优化后的车身侧倾角比优化前大0.029°，优化后的加权加速度均方根值比优化前小0.097 m/s2,并得出降低钢板弹簧刚度值可以提高平顺性结果，在前悬架加一个横向稳定杆可以提高操纵稳定性且不会影响平顺性的方案。汽车的实际牵引状态较理论模型更加复杂，在实际分析时要考虑车型的不完全对称性、惯量变化、噪声干扰等情况。