一种计及无功补偿的分布式电源优化配置方法
2020-06-20顾卫祥
张 潮,陈 静,顾卫祥
(1.南京工程学院,江苏省南京市 211167;2.新疆阜康抽水蓄能有限公司,新疆维吾尔自治区阜康市 830011)
0 引言
集中式发电和分布式发电相互补充是未来电网的发展趋势[1],对现有的配电网进行改造和接入分布式电源(Distributed Generation,DG)是改善能源结构、提高能源利用率的有效途径。DG的配置问题对系统的经济可靠运行具有重大影响,合理的位置接入合适容量的DG可以有效改善系统电压水平、降低系统网络损耗、提高系统可靠性[2~5],因此对DG选址定容问题的研究具有迫切性和必要性。
目前,针对DG的选址定容问题已经受到国内外学者广泛关注,文献[6~9]利用传统的数学方法包括梯度法、二次规划法、牛顿法和内点法对DG选址定容模型进行求解,这类方法有着严格的数学定义,对求解复杂的数学模型并不适用。近年来随着配电网结构复杂化、精细化,DG的规划中也需要建立复杂数学模型,各种智能启发式算法以其优越的非线性寻优能力被广泛应用在求解DG优化配置问题。文献[10~14]从不同优化目标出发,分别利用遗传算法、萤火算法、粒子群算法、蚁群算法、猫群算法对分布式电源接入配电网的配置进行优化,通过仿真算例证明在不改变电网架构的情况下,通过合理配置分布式电源可以有效改善配电网运行情况。
上述针对DG选址定容问题的研究提供了很多开创性思路,但同时也存在着一些问题。
(1)在实际工程中,DG接入配电网往往需要与储能系统配合布置,以提高配电网对可再生能源的消纳能力,这一方面已经成为当下的研究热点,已有文献对此研究仍显不足。
(2)随着大量出力呈现随机概率分布的DG接入配电网,配电网需要更多的无功补偿设备以维持系统电压稳定,所以在DG的规划过程中考虑无功补偿设备的配置显得尤为重要。
基于以上分析,本文在DG配置过程中,考虑无功补偿设备的配置,提出DG与储能协调配合下的DG配置优化模型,从经济成本和技术性指标考虑,建立了DG、储能系统、无功补偿设备建设成本最小,系统网络损耗最小,系统电压稳定指标最优的多目标优化模型,并提出一种基于概率分布策略的改进遗传算法,将该算法应用于求解DG的优化配置模型。
1 优化配置模型
系统网络损耗和系统电压稳定指标VSI同属于技术指标,采用加权组合优化,目标函数为F2。
分布式电源优化配置目标函数如下:

式中:F1经济成本函数,F2为技术指标函数。
1.1 经济成本

式中:F1为项目投资期内的总经济成本;f1为分布式电源建设成本;f2为储能系统建设成本;f3为无功补偿设备建设成本。
(1)分布式电源建设成本。
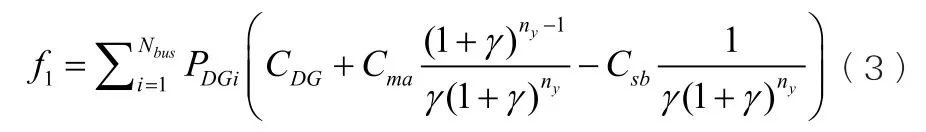
式中:Nbus为配电网节点数;PDGi为第i节点接入DG的有功功率;CGD为DG单位有功功率投资成本;Cma为DG单位有功功率维护成本;Csb为DG单位有功功率回收残值;γ为贴现率;ny为项目运行周期,为等年值求现比率;为将来值求现比率。
(2)储能系统建设成本。
本文考虑储能系统与DG协调运行,只在DG接入点配置储能系统,其配置既考虑DG的有功出力的转换成本,也考虑故障情况下短时间内维持接入点重要负荷继续运行的要求。
式中:fcn_inv为储能系统初始投资成本;fcn_ma为储能系统维护成本;fcn_rc为储能系统置换成本;fcn_cp为储能系统报废处理成本。
其中:
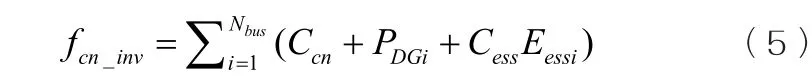
式中:Ccn为储能系统单位有功功率转换成本;Cess为储能系统单位容量投资成本;Eessi为第i节点接入储能系统的容量。
由于储能系统中储能单元运行周期小于分布式电源项目运行周期,需要在储能系统中考虑储能单元的置换成本fcn_rc。

式中:n为置换次数;T为运行周期。
为简化模型,储能系统维护成本fcn_ma、储能系统报废处理成本fcn_cp均按初始投资成本的一定比例进行计算。

式中:K为维护成本占初始投资的比例;L为报废处理成本占初始投资的比例。
(3)无功补偿设备建设成本。
本文在配置并联电容器组等静态无功补偿装置的基础上通过配置SVG以实现DG出力波动或故障情况下对配电网进行有效调压。并联电容器组与DG同时进行选址定容,SVG根据有功损耗对节点补偿无功的灵敏度选取位置[15]。

式中:fwg_c为并联电容器组建设成本;fwg_svg为SVG组建设成本。

式中:Qci为第i节点接入并联电容器组的容量;Cc为并联电容器组单位容量投资成本;Ccma为并联电容器组单位容量维护成本;Ccsb为并联电容器组单位容量回收残值。

式中:Qsi为第i节点接入SVG的容量;Cc为SVG单位容量投资成本;Ccma为SVG单位容量维护成本;Ccsb为SVG单位容量回收残值。
1.2 技术指标
(1)网络损耗。

式中:Ploss为配电系统网络损耗;l为系统支路数;rk为系统k支路电阻;Ik为系统k支路通过的电流。
(2)电压稳定指标。
DG接入配电网后也会改变相应节点的电压水平,若DG接入方式不当,极易造成系统电压失稳[16],文献[16]提供了计及分布式电源接入的配电网电压稳定性评估指标VSI,定义节点j的VSI为:

式中:fVSI_j为节点j的VSI;Qj为节点j送出的无功功率;Rij+Xij为线路ij的阻抗。
本文定义配电网的VSI为所有节点VSI的最大值,即fVSI。

故两者加权组合优化函数为:

式中:α1为网损权值;α2为配电网的VSI的权值;α1+α2=1。
1.3 约束条件
(1)功率平衡约束。

式中:Pi、Qi为节点i向系统注入的有功功率、无功功率;n为系统的节点数;Ui、Uj为节点i、j电压向量的幅值;Gij为节点导纳矩阵元素Yij的实部;Bij为节点导纳矩阵元素Yij的虚部;δij=δi-δj,为i、j两节点电压的相角差。
(2)电压约束。

式中:Umin和Umax为节点电压允许的上下限,一般电压正、负偏差的绝对值之和不超过额定值10%。
2 多目标遗传算法
2.1 遗传算法基本原理
遗传算法(GA)具有鲁棒性好,计算复杂度低,需要目标
函数的参数少等优点[17~19]。应用遗传算法进行优化主要包括5个步骤:初始化种群、构造适应度函数、选择操作、交叉操作、变异操作。
(1)初始化种群。
依据算法设定的参数,对种群进行初始化,内容包括DG的位置和容量、无功补偿设备的位置和容量四部分。
(2)构造适应度函数。
根据种群内个体信息构建分布式电源配置模型,以技术指标和经济指标作为评价种群内个体优劣的指标,即个体的适应度F。
(3)选择操作。
本文采用轮盘赌策略选择种群中的个体,即基于种群中个体的适应度大小决定个体选择概率,计算公式如式(18)、式(19)所示。

式中:Fi为种群中第i个个体适应度;k为系数;由于适应度值越小越好,所以以fi取代Fi,pi为个体被选中的概率。
(4)交叉操作。
本文交叉策略采用实数交叉法,假设第m个个体am和第n个个体an在第j个位置进行交叉,其操作过程如式(20)所示。

式中:b为0,1之间的均匀分布的随机数。
(5)变异操作。
假设第i个个体的第j个部分aij发生变异,其操作过程如式(21)所示。

式中:amax、amin为aij的上下界;r为0,1之间的均匀分布的随机数。
其中,算法变异操作采用下式:

式中:r2为[0,1]之间的随机数;g和Gmax分别为当前迭代次数和最大迭代次数。
2.2 改进遗传算法
通过式(20)和式(21)可以看出,基本的遗传算法交叉、变异操作针对所有个体执行,在算法后期,极有可能因个体交叉,变异不当,导致算法收敛速度变慢,存在精度不高的问题。在本文算法中,将保留每一代种群中适应度最高的个体不参加交叉、变异,其余个体按照概率µ进行交叉、变异操作,概率公式按式(23)计算。

式中:µi,Fi为个体i进行操作的概率及适应度值;Fmax,Fmin个体适应度得最值。
当满足µi>rand时,个体进行交叉、变异操作,rand为[0,1]之间随机产生的数。算法流程如图1所示。

图1 算法流程图Figure 1 Flow chart of algorithm
3 算例分析
本文选取IEEE-33节点配电系统为研究对象。未接入分布式电源时系统初始网络损耗和电压稳定指标分别为202kW和0.1363,为避免网络损耗和电压稳定指标因数量级差别导致误差,分别以与各初始值的比值作为优化指标进行加权,分布式电源均视为PQ节点,其功率因数为0.9。
3.1 参数设置
分布式电源在规划时,分布式电源投资成本为12500元/kW,维护成本为2000元/kW,回收残值为650元/kW,项目周期为20年,贴现率为6.7%[3][11];储能功率转换成本为2142元/kW,储能容量设置为保证接入点负荷2小时供电[20],容量投资成本2210元/kWh,维护比例K为10%,报废处理比例L为5%,设备使用年限为8年[20][21];电容器组投资成本为60元/kvar,维护成本为10元/kvar,回收残值为10元/kvar,SVG容量投资成本为250元/kvar,维护成本为20元/kvar,回收残值为20元/kvar,设备使用年限为 25 年[22],。
算法设置中,种群大小为100,存储档案大小为70,最大迭代次数为100,从2~33节点中选取5个位置安装分布式电源,1个位置按照电容器组,根据有功损耗对节点补偿无功的灵敏度选取SVG安装位置。
3.2 多目标优化结果及分析
根据本文提出多目标优化模型,按照改进MALO算法进行求解并与原始MALO求解结果进行对比,结果如图2所示。

图2 非劣解分布情况Figure 2 The distribution of the pareto solutions
采用文献[22]中的模糊贴近度对非劣解集进行筛选,得到的最优配置方案如表1~表3所示。

表1 DG配置方案Table 1 Allocation scheme of DG

表2 储能系统配置方案Table 2 Allocation scheme of energy storage system

表3 无功补偿设备配置方案Table 3 Allocation scheme of reactive power compensation equipment
表2中,储能系统的容量按照在DG退出运行后,保证接入点负荷2小时供电进行规划[20]。
表3中,电容器组每组容量为15kvar,在有功损耗对节点补偿无功的灵敏度较大的6号节点接SVG,参考文献[15]实例分析,选择接入容量为500kvar较为合适。
按照上述配置结果,将DG、储能系统和无功补偿设备接入IEEE-33配电系统,结果如图3和表4所示。
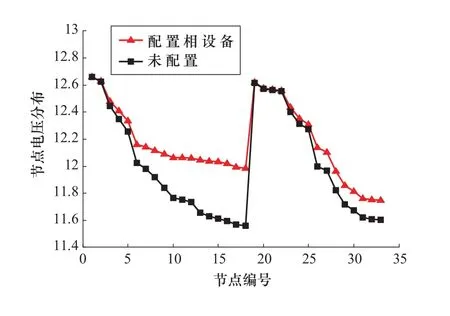
图3 电压分布Figure 3 Voltage distribution

表4 技术指标Table 4 Technical indicators
3.3 无功设备调压有效性分析
为了验证本文提出的无功设备配置的有效性,采用上述规划结果,针对最极端情况进行分析:DG因故障退出运行。
假设3、13号节点DG退出运行,采用无功设备优化电压分布,结果如表5和图4所示。
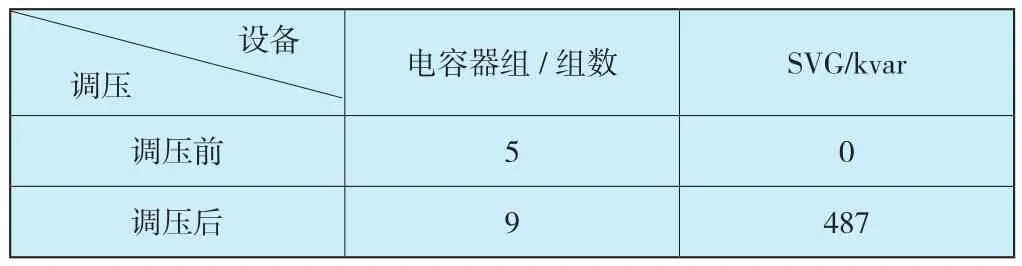
表5 无功设备参数Table 5 Parameters of reactive power compensation equipment

图4 优化前后电压变化Figure 4 Voltage change before and after optimization
由图4可以看出,部分DG退出运行后,系统局部电压水平发生恶化,本文通过设置无功补偿设备可以有效改善局部电压水平。
4 结论
本文考虑储能与DG配合布置,无功设备参与选址定容,建立了DG、储能系统、无功补偿设备建设成本最小,系统网络损耗最小,系统电压稳定指标最优的多目标数学模型,并应用改进遗传算法求解该模型,分析表明。
(1)改进多的遗传与原算法相比,有效地避免了算法在中后期陷入局部最优,具有更高的精度。
(2)DG配置过程中,考虑储能系统与DG协调配合的优化模型,更符合当前工程实际,其接入配电网,可以改善配电网运行状况,提高系统稳定性。
(3)DG配置过程中,考虑无功补偿设备的接入可以在配电网原有无功不足情况下,应对DG出现出力波动或故障时电压恶化的状况,在保证系统稳定运行的情况下,提高DG利用率,实现DG就地消纳。
