基于Chambolle-Pock算法框架的高阶TV图像重建算法

席雅睿，乔志伟，温 静，张艳娇，杨雯晶，闫慧文

（山西大学计算机与信息技术学院，太原 030006）

（∗通信作者电子邮箱zqiao@sxu.edu.cn）

0 引言

计算机断层成像（Computer Tomography，CT）作为最为先进的无损检测手段，应用于医学界和工业界。在医学领域，其要求在保持重建图像精度的同时尽量减少对于病患的辐射剂量。而目前，基于滤波反投影（Filtered BackProjection，FBP）为经典的解析法依然广泛应用于医学和商用CT 中。在传统奈奎斯特采样定理的要求下，应用解析法稀疏重建高精度的图像是十分困难的事情，会产生条状伪影［1-2］。随着压缩感知（Compressed Sensing，CS）理论的提出，全变分（Total Variation，TV）最小算法成为稀疏重建的研究热点［3］。Sidky等［4］提出了TV 最小重建模型，在仿真状态下实现了高精度稀疏重建。之后，Sidky 等［5］完善了该算法，详细给出了ASDPOCS（Adaptive Steepest Descent-Projection Onto Convex Sets）算法的伪代码，并将其应用到三维锥束CT 中。随后，有大量的TV 变体以及求解的优化算法被提出，如：Chambolle 等［6］提出了原始对偶优化算法。Sidky等［7］利用CP（Chambolle-Pock）优化算法去求解重建模型，并推导出一系列的算法实例。Tang 等［8］设计了一种基于CP 框架的对偶邻近点算法应用于全变分图像重建。Sidky 等［9］又提出了一种约束最小的TpV（Totalp-Variation）模型，并使用CP 算法对模型进行求解。宋文琪等［10］对于基于CP 算法的TV 重建算法进行研究，并且与传统的FBP 算法进行了详细的比较。乔志伟［11］设计了一种TV 约束的数据分离最小TV 模型，推导了CP 算法的实例，并对该模型在重建精度、算法收敛性等方面进行详细研究。这些TV 变体的提出以及优化算法的改进极大地促进了稀疏重建的发展。

然而，在实际的重建过程中，人们发现TV 算法有时会引入块状伪影，尤其在图像去噪领域中，此现象尤其明显，这引起了很多学者的注意并力求压制此效应，如：Chan 等［12］提出了基于高阶TV（High-Order TV，HOTV）的图像复原模型；Lysaker 等［13］提出了应用高阶TV 去除图像噪声，该模型有效去除了块状伪影，同时保持了图像平坦区域的光滑度；Papafitsoros 等［14］针对图像的修复问题详细比较了传统TV 与HOTV 的区别，并采用Split Bregman 框架进行求解；胡悦等［15］提出了基于增广拉格朗日乘子的快速高阶TV模型，该模型能够高效去噪并且一定程度上提高了算法的速度。HOTV 算法已经在图像处理领域中得到大量的使用，并且其不仅可以减小梯度效应、提高图像的质量而且对于图像去噪和图像复原都有很好的效果；但是HOTV 算法并没有在图像重建领域中展开深刻的研究。

ASD-POCS 算法是一种有效约束的TV 最小图像重建模型的求解算法，它使用ART（Algebra Reconstruction Technology）算法让数据残差逐渐下降，并使用自适应梯度下降算法让图像的TV值逐渐下降，最终找到数据保真约束下的TV 范数最小的最优解；但是ASD-POCS 算法往往需要凭借经验去调节参数，并且其ART 部分由于需要逐根射线处理，无法并行改造，需要耗费大量时间。然而，CP 算法其本身是严格按照数学公式推导而来，不需要根据经验去调节参数。

为压制TV 算法引起的块状伪影，解决ASD-POCS 调节参数问题，本文提出了一种基于CP 框架的HOTV 算法，并详细地推导了该算法，进一步揭示了算法的性能。本文以二阶梯度构建二阶TV 范数，并采用CP 算法对模型进行求解。为进一步比较其性能，采用基于波浪背景的Shepp-Logan 模型、灰度渐变模体以及真实CT图像模体共三种模体作为实验模体，分别在理想投影数据与含噪投影数据下详细地对CP-HOTV算法与CP-TV算法开展了定性和定量的评估。

1 相关知识

1.1 成像模型

本文以二维平行束CT重建为研究对象。已知离散-离散（Discrete to Discrete，D2D）的成像模型是将投影和图像均看成离散函数，则D2D 模型本身就是一个线性方程组。那么D2D成像模型可以被表示为：

其中：g是大小为I的列向量，表示投影数据；u是大小为J的列向量，表示图像像素；M是大小为I*J的矩阵，表示系统矩阵。Mi，j即为第j个像素对第i个投影测量的贡献。本文中用Siddon射线驱动法求取系统矩阵［16］。

D2D成像模型本身是一个线性方程组。在实际情况中这个方程组往往是巨大的、欠定的。如图像自身大小为256×256，投影数据也为256×256，则由式（1）可知其系统矩阵大小为4 GB。这是一个巨大的且直接求逆不可行的线性方程组。而在稀疏重建中，成像模型就是一个有无数解的欠定线性系统。成像系统的噪声更会将此线性系统变成一个病态的线性系统，鉴于上述原因，为获得更高的重建精度，需进一步将此模型建模为一个最优化问题。

1.2 TV最优化模型

根据上述成像模型，对于离散图像u约束的TV 最优化模型可表示为：

其受下述不等式约束：

若设图像大小为n*n，s∈[1，n]，t∈[1，n]，us，t表示第s行、第t列的像素，则可定义为：

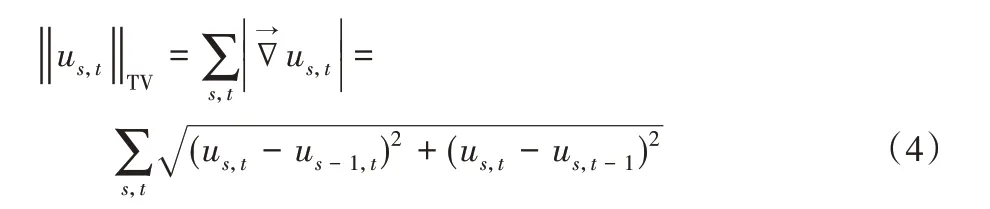
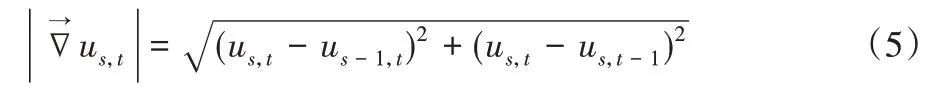
式（5）表示图像每个像素的梯度。

1.3 约束的CP算法求解TV模型

CP 算法是一种基本-对偶的形式，其最小化和对偶最大化可定义为：

式中：x、y分别为线性空间X、Y中向量；K为X空间到Y空间的线性变换；G和F为非平滑凸函数；“∗”表示凸共轭。则可得基本-对偶问题的一般鞍点最优化问题可表示为：

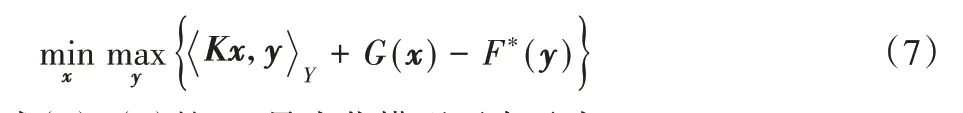
则式（3）～（4）的TV最小化模型可表示为：

则利用CP 算法求解TV 模型的整个目标函数可表示为F(Kx)形式，有：

TV最小化问题的F1函数、F2函数可表示为：

那么，式（3）最接近映射proxσ为：

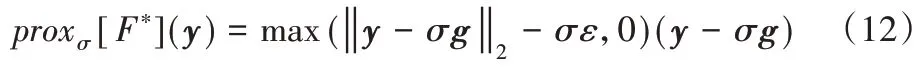
其中，σ为CP 算法的非负参数。上述详细推导过程可参考Sidky等发表的相关研究［7］。

2 本文方法

2.1 HOTV最优化模型设计

为了进一步求解1.1 节中D2D 巨大的线性方程组，结合HOTV 算法在图像处理领域的良好效果，本文提出了一种约束的HOTV最小模型，可表示为：

现定义图像的HOTV 范数是图像二阶梯度大小变换的l1范数：

其中：D1和D2均为N*N的矩阵，分别为沿着x和y轴方向的离散梯度变换。

设图像大小为n*n，s∈[1，n]，t∈[1，n]，us，t表示第s行、第t列的像素，则D1变换可表示为：

则D2变换为：

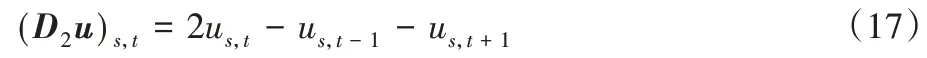
那么图像的离散梯度变换可表示为：

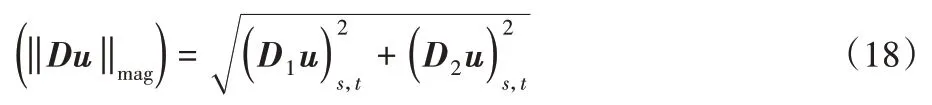
则图像的HOTV范数可表示为：

以128×128 的Shepp-Logan 图像为例，其二阶梯度大小图像如图1（c）所示。

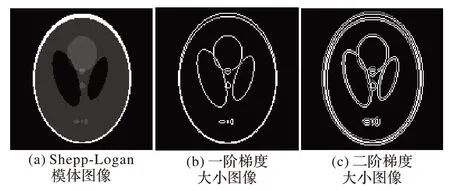
图1 Shepp-Logan模体及其梯度大小图像Fig.1 Shepp-Logan phantom and its gradient magnitude images

比较图1（b）和图1（c）可看出，一阶和二阶梯度大小图像均可表示边缘信息，但是两者提取的边缘特征有较大的区别，这就决定了TV算法和HOTV算法会有不同的稀疏重建性能。

2.2 HOTV重建模型的Chambolle-Pock求解算法

研究表明，总变差最小化在凸变分成像方法中起着重要作用，其优势在于允许在求解过程中出现明显的不连续，这对于很多成像问题至关重要，因为边缘往往代表着重要的特征。而本文设计的HOTV 重建模型有更好的保边性能。病态的反向成像问题一般可以分为两类：凸问题和非凸问题。而凸问题相较于非凸问题的优点在于其可以计算出全局最优，在很多情况下，具有良好的精度和合理的时间，且独立于初始化，因此凸问题解决方案的质量将完全取决于模型的准确性。本文中利用约束的CP 算法对HOTV 重建模型进行求解。CP 算法是一种原对偶的优化算法，该算法具有收敛性保证，提供了非启发式的收敛检查-对偶间隙。则根据上述理论，本文设计CP-HOTV算法如算法1所示。

算法1 HOTV-CP算法。

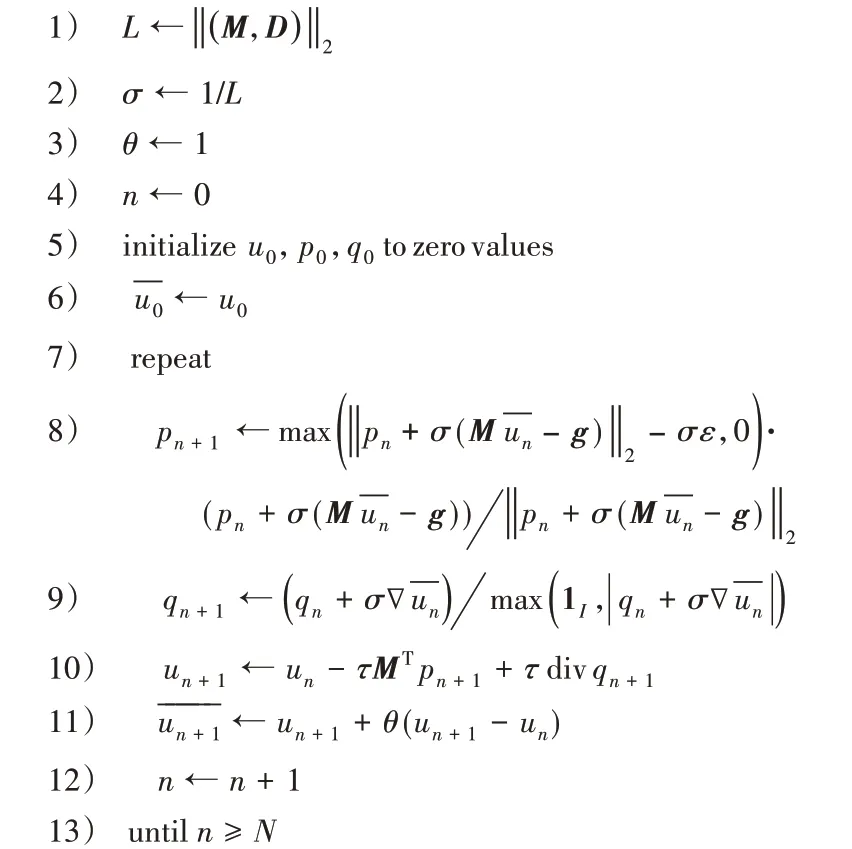
其中：L为系统矩阵M和2.1节所求D的二范数；τ和σ为算法的非负参数；θ为参数，θ∈[0，1]；n为迭代次数；u0，p0，q0和初始值均为0，8）～11）行对其进行更新。算法中所有参

数详细说明请参考文献［11］。

2.3 图像质量的评价标准

本文中将以均方根误差Root Mean Square Error，RMSE）和结构相似性（Structural SIMilarity，SSIM）作为重建质量评估判据，计算式如下：

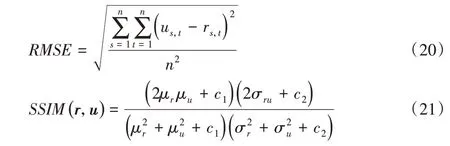
其中：u为重建图像；r为真值图像；μr和μu分别为r、u的平均值；和分别为r、u的方差；c1和c2是为了防止分母为零的常数。

3 实验与结果分析

为了进一步验证HOTV 算法的性能，本文采用了基于波动背景的Shepp-Logan 模体、灰度渐变模体以及真实CT 图像模体这三种模体，分别在理想数据投影和含噪数据投影两种情形下进行稀疏重建。

3.1 理想数据稀疏重建

基于波动背景的Shepp-Logan 模型是在传统的Shepp-Logan 模体上加入波动背景；灰度渐变模体的外部是线性渐变，内部是由小正方形中心到其四条边中心点的线性渐变；而真实CT 图像模体是将现实中的CT 图像作为模体。三种模体的大小均为128×128。本文实验室采用的都是平行束的扫描方式，其中成像的几何参数为：在360°的采样角度范围内，均匀地采集了30个角度，每个角度的投影信号为128个测量值；探测器探源大小归一化为1；图像大小也归一化为1。使用TV 算法和HOTV 算法进行稀疏重建，迭代次数设为5 000 次，其重建结果如图2 所示，表1 为迭代结束后重建结果的RMSE值和SSIM值。

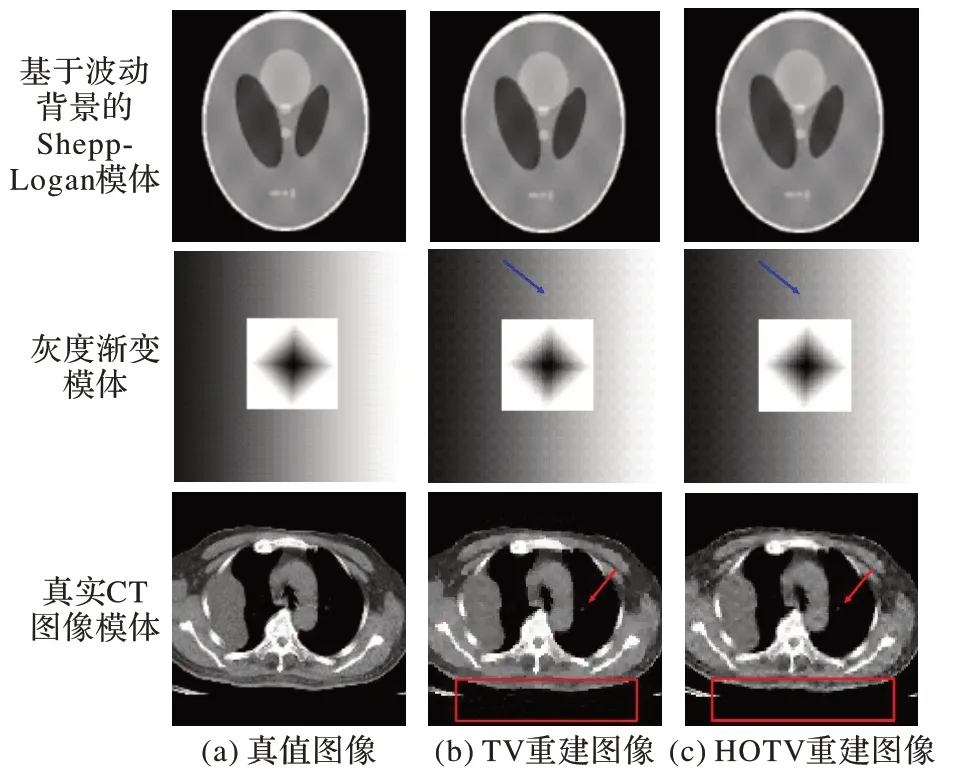
图2 理想数据投影下三种模体重建结果Fig.2 Reconstruction results of three phantoms under ideal data projection

图2 给出了传统的TV 算法和HOTV 算法的重建结果。由图2 可以看出，对于基于波动背景的Shepp-Logan 模体，其HOTV 重建结果与TV 的重建结果视觉质量相当；但是对于灰度渐变模体，可以明显发现，TV 重建图像中有很多条形伪影，而HOTV 重建图像很平滑；对于真实CT 图像模体，由于模体本身复杂度远高于其他两组，其图像质量均不算太高。比较其矩形框部分，HOTV 重建图像结构清晰且保留了更多细节信息，而TV重建图像中有多处块状伪影。

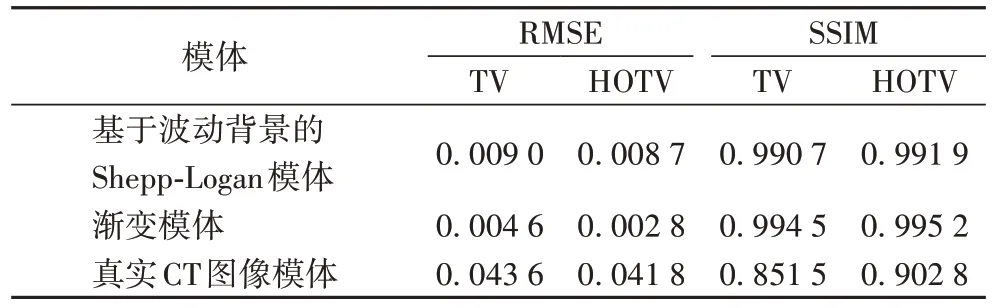
表1 理想数据投影下迭代结束后不同模体的RMSE值和SSIM值Tab.1 RMSE and SSIM values of different phantoms after iteration under ideal data projection

表1中，当迭代结束后，会发现对于三种模体，HOTV重建图像的RMSE 值均低于TV 重建图像的RMSE 值；当迭代结束，对于三种模型，相较于TV 重建图像，HOTV 重建图像的SSIM 值更接近于1，表明HOTV 重建图像的图像结构与真值图像更相似。

通过定性定量比较可知，对于基于波动背景的Shepp-Logan 模体以及灰度渐变模体这一类含有灰度渐变过渡区域的模体，HOTV 算法能提高其重建精度；而对于复杂结构的医学图像，相较于传统的TV 算法，HOTV 算法能有效减少块状伪影的同时取得更高的重建精度。

3.2 含噪数据稀疏重建

为进一步评估在特定噪声强度情形下HOTV 算法的重建性能，本文将对投影数据分别加入方差为0.01、0.02、0.03、0.04 和0.05 的高斯噪声，通过比较TV 算法和HOTV 算法的重建性能，分析二者的抗噪能力。

为了更深刻地比较两种算法的抗噪性，本文还将对投影数据分别加入λ值为1、3、5、7 和9 的泊松噪声，定性、定量地对HOTV 算法和TV 算法的重建质量进行比较。为简便起见，此部分只给出灰度渐变模体的重建结果。图像重建的成像条件及参数设定与2.1 节部分相同，方差为0.01 的高斯噪声和λ值为1 的泊松噪声情形下的重建图像如图3 所示，表2 为迭代结束后重建图像的RMSE值和SSIM值。

图3 含噪数据投影下灰度渐变模体重建结果Fig.3 Reconstruction results of grayscale gradual changing phantom under noisy data projection

从图3 和表2 可知，相较于TV 算法，HOTV 算法的重建精度更高。加入其他强度高斯噪声情形下的图像重建效果与上述实验效果类似，故不再展示相应重建结果。表3 给出了各种强度高斯噪声情形下的HOTV及TV算法重建图像的RMSE值以及SSIM 值。表4 给出了各种强度泊松噪声情形下的HOTV 及TV 算法重建图像的RMSE 值以及SSIM 值。无论是高斯噪声还是泊松噪声，均可以看出，HOTV 算法可以更高精度地稀疏重建图像，这表明HOTV 算法具有更强的抗噪能力。

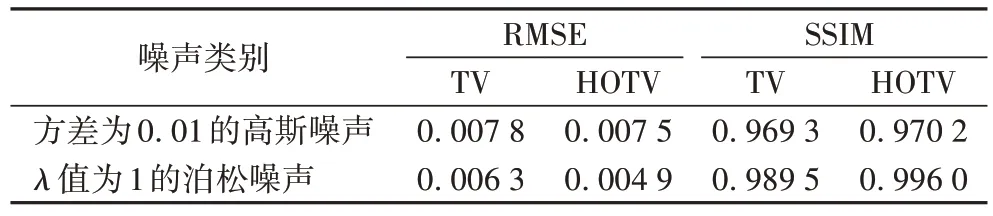
表2 含噪数据投影下重建图像的RMSE值和SSIM值Tab.2 RMSE and SSIM values of reconstructed images under noisy data projection

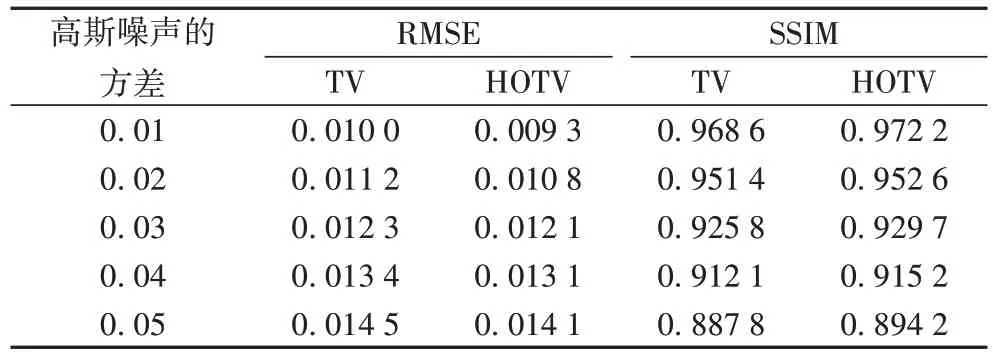
表3 不同强度高斯噪声情形下两种重建算法的重建精度比较Tab3 Reconstruction accuracy comparison between two algorithms under different intensities of Gaussian noise

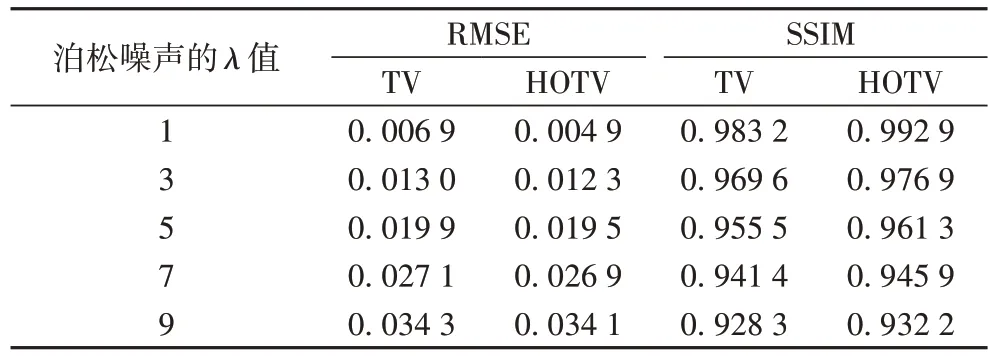
表4 不同强度泊松噪声情形下两种重建算法的重建精度比较Tab.4 Reconstruction accuracy comparison between two algorithms under different intensities of Poisson noise

3.3 CP-HOTV算法的收敛性

为了描述CP-HOTV 算法的收敛性，通过观察重建过程中RMSE 值的迭代走势，揭示CP-HOTV 算法的迭代规律。以基于波动背景的Shepp-Logan 模型为例，图4 为CP-TV 和CPHOTV重建图像的迭代走势。

图4 重建图像的RMSE随迭代次数的变化Fig.4 RMSE of reconstructed image varying with number of iterations

从图4 可以看出：CP-TV 算法与CP-HOTV 算法的RMSE迭代过程中均在不断下降；迭代过程中，很明显CP-HOTV 算法的RMSE 值几乎一直小于CP-TV 算法的RMSE 值；迭代结束时，CP-HOTV 算法的RMSE 值为0.008 7，而CP-TV 算法的RMSE 值为0.009 0。综上可以得出，CP-HOTV 算法在整个重建迭代过程中收敛精度更高。

3.4 算法运行时间的比较

在实际的医学CT 和工业CT 中，算法的运行时间也是衡量算法的重要指标。为了更全面地对CP-TV 算法与CPHOTV算法进行比较，表5中以三种模体在理想数据投影下的算法运行时间为例。

表5 不同算法针对不同模体理在想数据投影下的运行时间对比单位：sTab.5 Running time comparison of different algorithm for different phantoms under ideal data projectionunit：s

由表5 可以得出，在理想数据投影下，CP-TV 算法和CPHOTV算法在5 000次迭代结束后，CP-HOTV算法的运行时间略长，且随着模型难度的加深，其算法的运行时间也越来越长。相较于CP-TV 算法，CP-HOTV 算法中运用的是HOTV 范数，其求解过程较为复杂，但却有更高的精确度。

4 结语

本文提出了一种数据保真约束的HOTV 最小图像重建模型，进而设计了相应的CP求解算法。该算法在压制块状伪影的同时在一定程度上提高了重建精度。复杂医学图像中往往存在很多灰度线性渐变或波浪式渐变的区域，而HOTV 算法是从数据保真项所定义的凸集中选择HOTV 最小的图像，所以其更适合重建灰度波动特征明显的图像。本文研究的目的是探索HOTV 算法的性能及可能的重建优势，故设计的三种模体均含有灰度波动特征。本文采用的CP算法，虽然解决了ASD-POCS 算法凭借经验调节参数的问题，但是占用大量内存。若使用图形处理（Graphics Processing Unit，GPU）加速算法，将会使原有算法占用更小的内存且有更快的运行速度，这将是迭代法日后发展的趋势，也是我们进一步的研究方向。