基于博弈论及Q学习的多Agent协作追捕算法

郑延斌，樊文鑫，韩梦云，陶雪丽

（1.河南师范大学计算机与信息工程学院，河南新乡 453007；2.智慧商务与物联网技术河南省工程实验室，河南新乡 453007）

（∗通信作者电子邮箱525845701@qq.com）

0 引言

多Agent 协作追捕问题是多Agent 协调与协作研究中的一个典型问题，在军事、工业、农业等方面都有典型的应用。受到国内外研究者的广泛关注［1-7］。根据逃跑者的数量，多Agent 协作围捕问题可以分为单逃跑者围捕和多逃跑者围捕问题，本文关注在有障碍物条件下的单逃跑者协作围捕问题。在单个逃跑者围捕中，当逃避者不具备学习能力时，围捕者可以根据逃避者的逃跑策略制定相应的围捕策略，其追捕效率高；当逃避者具有学习能力时，环境中的障碍物可以同时被追捕者和逃跑者利用，追捕者可以利用障碍物阻挡逃跑者，逃跑者同时可以利用障碍物躲避追捕者，同时逃跑者又可以根据围捕者的策略来改变自己的逃跑策略，因此追捕的效率低。

针对逃跑者具有学习能力使得追捕效率降低的问题，国内外研究者提出了许多解决可感知环境下的多Agent 协作围捕的方法，可以分为两类：

1）利用强化学习方法探索多Agent 协调行为，解决单逃跑者的追捕问题［8-11］。如：Asl 等［9］提出了一种基于强化学习的多Agent协作围捕方法，该方法利用Q学习方法建立一个共享的Q值表，用于记录逃避者过去的行为路线，每个围捕者在选择自己的围捕策略时，不是从固定的动作集中选择，而是从已经建立好的Q值表中来选择，与同类型的追捕算法相比较，追捕效率更高。Bilgin 等［10］使用强化学习方法对多Agent 追捕问题进行了研究，用Q-Learning 与资格跟踪相结合方法，首先在多Agent 团队中使用并行学习的方式，每个Agent 独立选择自己的行为，并收到相应的反馈信息（环境的奖励或惩罚），并利用这些反馈来更新每一个成员的action-value 矩阵；其次，为每个Agent 存储临时的行为轨迹（存储其行为的临时记录），当资格跟踪发生错误时返回奖励或惩罚，由于过去的追捕行为会随着时间的推移而消失，因此在Q-Learning 算法中加入衰减率。实验结果证明了该算法的有效性，表明了在同等环境下不同学习率和衰减值的差异性。Qair等［11］提出了一种基于自组织特征映射（Self-Organizing Feature Mapping，SOFM）和基于Agent 群角色隶属函数（Agent Group Role Membership Function，AGRMF）模型的增强学习的移动多智能体追踪方法。该方法基于SOFM 和AGRMF 技术，促进了追求者群体的动态组织，并使追求者群体根据自己的意愿进行规避。这有助于克服在AGRMF 模型运行过程中，当目标过于独立时，追求者不能完全重组的缺点。此外，还加入了奖励功能。在群体形成后，应用强化学习得到每个Agent 的最优解。捕获过程中每一步的结果最终都会影响AGRMF，从而加快竞争神经网络的收敛速度。

2）基于博弈论的多Agent 协作追捕策略［12-15］。如：Fang等［13］针对多机器人协作围捕的时间会受到每个自利的机器人动作选择的影响，提出了一种基于量子博弈的方法，将经典战略空间扩展到量子伙伴的范围，确保机器人的行为策略收敛到最优平衡点，消除随机性和盲目性；晏亚林［14］通过将逃跑者加入“拒捕”行为，且改进了有效包围和距离影响的权重，在可感知的环境下将追捕问题转化为博弈问题，提高了围捕的效率；Hakli［15］提出了一种基于规划和博弈团队推理相结合的协同规划方法，该方法从构建一个群体计划开始，从中派生出它们的子计划，个体在群体的计划中执行它们各自的部分，适合在可以观察到彼此行动的情况下的合作，在实际情况中能够更像人类一样进行有效的联合动作。

多Agent 追捕环境中，追捕者和逃跑者都具有学习能力，故追捕者的协作追捕行为受逃跑者的逃跑的影响，逃跑者的行为也会受到障碍物追捕者以及障碍物的影响。上述的方法在强化学习方面虽然考虑到了对逃跑者的行为策略进行学习，但是未能考虑到在动态环境中追捕双方受到的相互影响，及资源冲突的问题；在博弈论方法方面，考虑到了团队之间的协作，但纯博弈的思想会有收敛速度慢的问题。然而，博弈论为这种具有相互影响的决策性提供了很好的数学模型，而强化学习可以让Agent 在特定环境中，根据当前的状态，做出行动，从而获得最大回报；另外，博弈论的核心是均衡局势的问题，故为了达到均衡，追捕者和逃跑者应相互学习，从而使得自身利益最大化。因此，研究者提出将博弈理论与强化学习进行有效结合，考虑到在动态环境中受到的相互影响，并通过学习的方法将追捕者的策略进行迭代更新，设定出具有针对性的追捕策略，将策略作为博弈论中Agent 可选择的动作策略，能够有效地完成多Agent的协作追捕任务。

本文提出了一种基于博弈论及Q 学习的多Agent 协作追捕算法，来解决可感知环境中，逃跑者和追捕者都具有学习能力的情况下，多Agent 的协作追捕问题。该算法利用Agent 的属性以及任务的需求，利用博弈的相关知识建立追捕团队；对追捕成功的多条运动轨迹进行学习，并把学习到路径轨迹调整到追捕者可选择的可执行策略集中，更新追捕者的策略；通过求解博弈得到Nash 均衡解。同时针对在求解中可能存在多个均衡解的问题，加入了虚拟行动行为选择算法，选择最优的均衡策略。在实验平台上对本文提出的算法进行分析实验，验证了本文算法的合理性及有效性。

1 相关基础

1.1 博弈论基础

博弈论（Game Theory）又称“对策论”，它研究的是在决策者的行为之间发生相互作用时，各个决策者所做对策的问题［16-17］。

定义1博弈可以用一个三元组来描述，即。

其中：P表示所有局中人的集合P={p1，p2，…，pn}；S表示局中人可行的策略集S={S1，S2，…，Sn}；每个Agent 的策略可以形式化为()；U表示局中人的支付函数U={U1，U2，…，Un}。

定义2Nash均衡。

设G=，如果存在一个联合行为a*∈S，满足条件：∀I∈P，∀ai∈S，)≥U(ai，ai-1)，则称a*为博弈G的Nash均衡（Nash equilibrium）。

Nash 均衡是博弈的稳定解。只有当所有的局中人都预测到某一个特定的Nash均衡出现的情况下，Nash均衡才会出现，当这样的一个Nash 均衡出现，任何一个局中人偏离这个策略组，其收益函数不会变大，因此一旦所有的局中人组成了Nash均衡，任何一个局中人都不会擅自偏离。

1.2 Q学习

机器学习（Machine Learning，ML）是当前人工智能领域的一个热点问题。根据数据类型的不同，以及对一个问题建模方式的不同，将机器学习分为三种类型：监督学习（Supervised Learning，SL）、非监督学习和强化学习（Reinforcement Learning，RL）。

强化学习（RL）主要强调智能体能基于环境而行动，以取得最大化的效益，即：智能体在学习过程中通过环境给予的奖励或惩罚，不断尝试，逐步形成对刺激的预期，从而产生能获取最大回报的策略［18-19］。

强化学习中Q-learning是一种具有代表性的算法，它主要由四种部分组成：1）Q表：Q(s，a)为状态s下执行a动作的累积价值；2）选择动作；3）做出动作，环境反馈；4）环境更新。在其过程中Agenti观察周围环境，执行动作策略集中的动作。在t时刻，Agenti执行动作at，同时反馈收益R（St，at），更新Q值表，重复上述过程，直到任务结束。其中Q（St，at）的值可用公式表示为：

式中：a为动作策略集中的某一动作；常量参数γ（0≤γ≤1）称作影响因子。在Agenti训练学习过程中，选择最大Q值的动作进行迭代训练。

2 基于博弈论及Q学习的协作追捕算法

2.1 追捕问题描述

假定在一个多Agent 协作环境X中，由M个Agent 构成的追捕者用集合R={R1，R2，…，Rn}表示，由N个Agent 构成的逃跑者用集合T={T1，T2，…，Tn}表示。环境内有形状和大小任意的固定障碍物，其位置映射关系为m：X→{0，1}，指定所有x∈X，m(x)=1表示位置x是障碍物。时间可离散化，并用t∈T={1，2，…}表示，规定任意Agent 在每个时刻只能执行一个动作，原地不动或者移动到其相邻并未被占据位置。多个追捕者形成一个协作团队完成任务W，完成任务后可以获得一定的效用U。

将逃跑者被捕获定义为定义3。

定义3Ge(t)={Xe(t-1)}，t∈T。

定义3表明，当逃跑Agent在t时刻被追捕成功时，它只能运动到t-1 时刻所在的位置中，其中Xe(t-1)表示其逃跑Agent 在t-1 时刻所占据的位置，同时若能满足以下三个条件也可以认为是被捕获的。

1）在没有障碍物的情况下。

假设逃跑Agent 在t-1 时刻运动，其周围的呈三角形位置已经被其他追捕的Agent 占据，且相邻两个追捕Agent 的距离小于两个身长的长度，如图1所示。

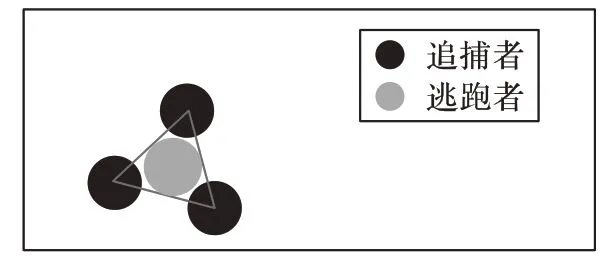
图1 没有障碍下追捕成功Fig.1 Successful pursuit without obstacles

2）在有障碍物的情况下。

假设逃跑Agent在t-1时刻，逃跑Agent的某一个或者不多于四个方向都存在障碍物，此时追捕Agent 占据其他可移动方向的位置，如图2所示。

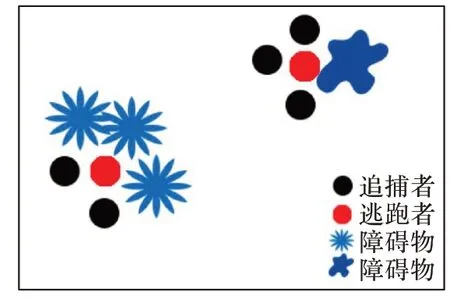
图2 障碍下追捕成功Fig.2 Successful pursuit with obstacles

3）在无法挣脱的情况下。

假设逃跑Agent 在t-1时刻，已经被团队形成围捕之势，其活动空间存在，但其运动的路径已经无法挣脱围捕圈，这种情况也可判定为已被抓捕。

2.2 障碍物问题描述

实验平台中会设定一些大小、位置不一的障碍物，用于模拟真实的环境。下面设定障碍物的一些属性：

1）由于实验环境设定得比较大，在环境中设定的障碍物不能占满整个环境。

2）环境中设定的障碍物不能全部聚集在一起。

由于障碍物没有布满整个环境，在没有障碍物阻挡的一些地方就会形成无障碍的状态。在无障碍环境下，追捕者只能靠自己运动才能将逃跑者围捕，其追捕难度就会比较大；相反，在有障碍的环境下，追捕者既可以利用障碍物对逃跑者进行围捕，逃跑者也可以利用障碍物躲避追捕者，因此平台中障碍物的大小、数量以及分布会对追捕者和逃跑者的运动产生影响，这种影响就会降低追捕的难度。在实验平台中障碍物的数量越多，逃跑者在某一特定的位置可选择的方向就越少，此时追捕者利用障碍物将逃跑者围捕的概率就变大；然而，障碍物比较分散的情况下，追捕者与逃跑者的可选择方向都会减少，此时对两者都是有影响的。

2.3 虚拟管理者

在整个追捕环境X中已经设立了M个追捕者和N个逃跑者，为了使追捕的环境趋于真实化，就需要有管理者同意安排并初始化障碍物的位置和大小，以及在追捕者团队中担任指挥的角色。

在多Agent 系统中建立一个虚拟管理者，此管理者不参与任何追捕活动，虚拟管理者的任务负责确定N个逃跑者、M个追捕成员，记录所有Agent 从开始到结束的轨迹路线，当追捕团队有多个均衡解时，虚拟管理者作为居中调度选择最优解。

2.4 追捕团队的形成

在多Agent 中选择一个Agent 来管理完成任务的分配，管理Agent 掌握所有Agent 的位置、能量、偏好等属性信息，但由于Agent 的自利性，了解所有Agent 的全部信息是不现实的，故采用基于拍卖的方式实现任务分配，管理Agent 了解所有的任务信息，负责发布任务，其他Agent 根据自己的能量、自身属性和已经发布的任务需求进行投标。具体算法如算法1所示。

算法1 任务分配算法。

步骤1 虚拟管理者将环境中的所有Agent 初始化为逃跑者与追捕者。

步骤2 虚拟管理者发布，并利用广播的方式告知未分配的任务Wi的信息，以及该项任务完成所能给予的报酬Uwi。

步骤3 追捕者接收到虚拟管理者的广播，预估该任务可能消耗的能量和所获得的报酬Uwi，根据自己剩余的能量以及偏好等属性选择愿意承担的任务来投标，并把投标的信息广播给虚拟管理者。

步骤4 虚拟管理者等待追捕者提交投标信息，若有投标信息，则进行步骤5；若无投标信息，转向步骤8。

步骤5 虚拟管理者设定投标价格为BP（Bid Price），并将每个任务中M个追捕者的投标从高到低进行排序。

步骤6 虚拟管理者选择n(n≤m)个追捕者分配给该任务，并将中标信息广播给追捕者，该追捕者的标志busy=1，不允许再投标其他任务。

步骤7 如果同一个Agent 向多个任务提交了投标，虚拟管理者计算Uwi-UPowi（UPowi为执行任务需要消耗的收益），选择能获得最大效用的任务分配给该追捕者。

步骤8 若所有的任务分配完毕，则转向步骤9；否则对未分配的任务进行分解，转步骤1。

步骤9 结束。

2.5 协作追捕算法

2.5.1 博弈模型的构建

在追捕环境中通过团队之间协作完成任务的追捕者，团队中一个追捕者的行为会受到其他追捕者的影响，同时逃跑者的行为也会受到追捕者的行为决策的影响。而博弈论为这种相互影响的决策行为给出了很好的数学模型［20］。

定义4多Agent协作围捕博弈模型，。

其中：P为追捕团队中追捕者的集合，P={1，2，…，n}；S为追捕者可能执行的策略集合；Si是团队中每个追捕者的动作策略，每个追捕者根据当前自己周围的环境和其他追捕者周围的环境做出相应的动作。每个Agent 的策略可以形式化为()，U是支付函数，表示执行策略之后的得失情况。

设多Agent 系统所处的环境为X，Xt表示多Agent 系统在时刻t所处的环境。

设Agent可观测到的环境状态的集合为St，为系统中在t时刻的联合观测，记为：。在动态复杂的环境下，多Agent 系统中的Agent 所获取的信息可能是完全的，也可能是不完全的。

设Agent 动作集合为A，Ai用于表示Agenti的动作集合，Agent 的动作集合用A表示，，从每个Agent 在时刻t所观测的环境采取的动作对环境产生的影响看，多个追捕者之间的联合行动也会对当前所处的环境的状态产生影响。

设状态转移函数为T，Tt：S×A→S，表示在某一特定的环境下，某个追捕者与其他追捕者之间通过协作对环境可能产生的影响。

设Agent 支付函数为U，Ui=S×A→U，表示Agenti在多Agent系统中为了完成任务所采取的行为后的收益情况。

Agent 的目标集合G={G1，G2，…，Gn}，Gi表示多Agent 系统中每个Agent 的目标，通常可以利用支付函数U来表示，每个Agenti之间的目标可能存在多种关系：当目标一致时，Agent 之间目标的完成是相互促进的；当目标冲突时，就会产生利益资源的冲突。

2.5.2 基于Q学习的可执行的策略集

在单猎物追捕问题中，需要在环境中随机生成M个追捕者，由它们组成一支协作追捕团队A。由于单猎物以是否具有学习能力分为智能化和非智能化。非智能化的逃跑者其逃跑运动轨迹一般比较固定，智能化的逃跑者运动轨迹不确定，会根据自身对环境的状态进行选择路径。因此，在其逃跑的策略集中加入强化学习算法，对其动作选择的策略集进行改进。

在t时刻可以进行移动的方向称为Agent 的策略集，其策略集就是其能进行决策的集合。t时刻逃跑者的策略集表示为St：

St包含｛Xa，Xb，Xat，Xbt｝

其中：0°≤Dir≤360°，供其选择的方向有360°；π=3.14；V表示速度。

由于追捕者无法获知逃跑者的状态-动作值Q，也就无法准确地找到适合的策略应对，其原有的策略集就显得比较宽泛，因此加入Q学习的方法对逃跑者的动作状态值进行学习，调整为具有针对性的追捕策略集。

由于逃跑者的逃跑策略都是未知的，因此，使用强化学习的方法对逃跑者的逃跑策略进行学习，制定适合追捕者的追捕策略。首先，在此算法中加入Step-T累积奖赏的学习任务，从逃跑者的初始状态出发，使追捕者经过有限次的学习获得一条具有Step-T的逃跑者的逃跑轨迹：

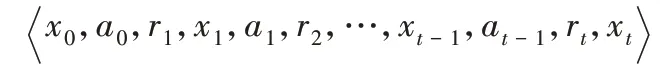
其次，记录轨迹中每一对状态-动作Q的累计奖赏之和，作为一次关于逃跑者累积奖赏采样值。当对逃跑者进行多次采样得到多条逃跑轨迹后，将对多次获得的累积奖赏采样值利用式（1）求取平均，得到Q值的估计。

由于要得到较好的动作-状态值函数的估计，就需要产生多条不同的轨迹，然而逃跑者选择的策略有可能是固定的，经过采样会导致追捕者得到的路线都是一致的。为了得到最优的策略，引入ε-贪心算法，以ε的概率从所有的动作中均匀地随机选择一个动作，以1-ε的概率选取当前最优动作，将已经确定的策略标记为“原始策略”。在原始策略中使用了ε-贪心算法的策略记为式（2）：

2.5.3 追捕团队成员避障策略

追捕团队成员在环境中进行抓捕以及逃跑者在进行逃逸的过程中，在t时刻其要运动到的位置可能被其他物体占领，这就有可能会发生碰撞，因此就需要根据所处环境的约束，进行实时有效的避障。传统的人工势场法的基本思想就是将追捕团队所处的环境充斥着混合势力场，环境中的逃跑者充斥着引力势场，方向由追捕者指向逃跑者；环境中的障碍物以及各个追捕者充斥着斥力势场，方向是由障碍物指向追捕者及逃跑者。分析传统人工势场法易出现局部极小点和目标不可达的原因，文献［21-22］给出了一种改进后的合力公式（3）如下：

式中：Fall为合力；Fg为虚拟目标点对Agent 的引力；α为方向向量的增益系数；derc为单位方向向量；β为斥力增益系数；Fol为障碍物点i对Agent的斥力。

这样既能保证追捕者趋向于逃跑者，又能避免环境中的所有Agent与障碍物发生碰撞以及追捕者之间发生碰撞。

2.5.4 支付函数

追捕过程中，双方需要一个标准来评估自己选择策略的优劣，博弈论中用支付函数实现这一功能，追捕者的目标是：1）判断逃跑者下一个时刻t的逃跑方向；2）预测下一点的位置中是否存在障碍；3）先将逃跑者在最短的时间内围住。而逃跑者的目标是有多条路径供其选择逃跑。双方具有不同的目标，且双方在一方受到利益损害时另一方并不一定有收益，因此可以认为追捕者与逃跑者之间博弈为协作博弈。

由于追捕者对于逃跑者的威胁程度主要体现在距离的远近、包围圈的好坏上，因此在支付函数中包含以下三个影响系数：

1）距离影响系数Kd。

当追捕者距离逃跑者的距离越近，那么它对逃跑者的威胁系数就越大；反之则越小。以此来定义距离影响系数，如式（4）所示：

其中：n为追逃环境中追捕者的数量；DPjEt表示t时刻第j个追捕者与逃跑者之间的距离。

2）有效包围系数KC。

由于成功追捕的条件是逃跑者在其周围已经没有其选择的逃跑方向，并且其可能的走步数在逐渐减少，此时的状态是追捕者逐步地接近逃跑者，并且已经在形成围捕的局势。以此来定义有效包围系数式（5）：

式中，Dir为可供其选择的方向。

3）速度变化系数KV。

在环境中逃跑者的运动由于受到人工势场的影响，其会受到合力Fall的作用；其次，追捕者的初始位置是随机的，有的追捕者就可能会出现在距离逃跑者较远的位置。为了保证能快速形成围捕的趋势，因此需要根据受到的合力Fall以及距离逃跑者的距离S及时地调整速度，其计算式定义如式（3）和式（6）～（7）。

式中：S表示追捕者与逃跑者之间的距离；tx、ty为当前逃跑Agent 的坐标位置，dx、dy为当前追捕者的坐标位置；α、β为影响速度V的权重值，在不同的局势下，追捕的侧重点不同。例如在距离较远的情况下，采取的策略以加速靠近为主；在距离缩小到一定的范围之后，采取的策略应该以形成包围圈为主。因此针对不同的情况设定不同的权重值。

定义支付函数U：

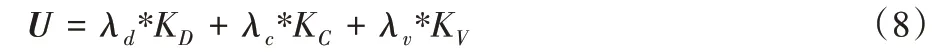
式中：λd与λc、λv分别代表不同的权重值，其中λd+λc+λv=1，权重的大小要根据在环境中遇到的情况进行调整。

2.5.5 逃跑Agent的追捕策略选择算法

追捕者与逃跑者在某t时刻选择各自的走步策略，追捕者根据定义的支付函数可以分别计算出追捕双方在不同的策略选择下追捕者的支付矩阵Ut。将t时刻的支付矩阵表示如式（9）：

根据博弈论中矩阵博弈的基本定理，一定存在混合策略意义下的解，通过排除法求解此矩阵，可得到t时刻局中人的最优策略。

2.5.6 基于虚拟行动的Agent行为选择算法

在上述的多Agent 协作追捕方法中，多个Agent 通过学习收敛到纳什均衡Q值。然而在协作追捕的博弈模型G的环境中，由Nash定理可知，博弈G至少存在一个Nash均衡解，因此每个Agent 通过学习都可能存在有多个纳什均衡的情况，当多个Agent 存在多个纳什均衡解时，就需要每个Agent 都会选择同一个纳什均衡解。

本节要考虑的问题是当博弈中存在多个纳什均衡解时，Agent 如何通过合适的策略保证最终选择同一个均衡解。在此，引入博弈学习中虚拟行动过程的概念，这种学习模型将有利于解决存在多个均衡解的问题。

虚拟行动模型中，多个Agent 处于有限重复博弈中，每个Agent 都会根据对手Agent 的历史行为，对在当前阶段对手Agent行动的概率分布进行预测和评估，并且会选择一个最优化其预测支付的行动。其评估的特定形式如下：Agenti有一个初始的加权函数，+，每次当对手Agent 选择策略S-i时，通过给每个对手相应的策略权重加1 对该函数进行调整，即式（10）。

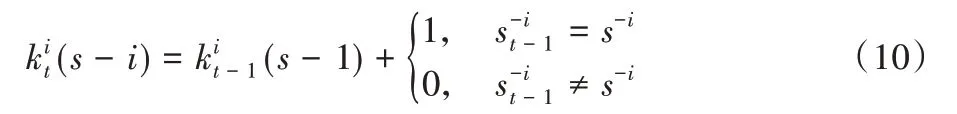
在阶段t，Agent赋予其他Agent采取策略S-i的概率为：

在虚拟行动中，Agent 仅仅跟踪对手Agent 的行动频率是不行的，还需要学习到这些概率分布，因此Agent 应该渐进地获取概率分布时相应的效用U。用D-i t表示Agenti的对手行动的经验分布。

在虚拟行动中某一时刻t，定义Agent 对其所评估的对手Agent的行为策略而言最优的行动集合为：

在重复博弈的过程中，每个Agent 相信对手Agent 的行为是一个未知的但固定概率分布的多重随机变量序列，这种序列可以通过式（10）、式（11）从行为历史中学到。Agenti在学习时刻t实际行为选择是它在t时刻关于对手Agent 行为策略的最优行动，如式（13），基于虚拟行动方法构建了Agent 行为选择算法如算法2所示。

算法2 基于虚拟行动的Agent行为选择算法。

将上述的方法进行整合，用一个完整的算法3 表示整个多Agent协作追捕算法的过程。

算法3 基于博弈论及Q学习的协作追捕算法。

步骤1 初始化生成逃跑者和追捕者；令其动作-状态Q(x，a)=0，count(x，a)=0，π(x，a)=1 |A|。

步骤2 根据算法1建立追捕团队，并建博弈模型。

步骤3 根据成功捕获的条件判断逃跑者是否被捕获，如果已经被捕获，则结束任务；否则，则进行步骤4。

步骤4 利用式（4）～（5）、式（7）控制速度变化，并向逃跑者的位置进行移动。

步骤5 执行策略π，产生轨迹。

步骤6count(xt，at)=count(xt，at)+1，利用式（1）对Q(x，a)值策略进行更新。

步骤7 判断能否形成完整Step-T运动轨迹，若形成则转至步骤8；否则继续进行步骤4～7。

步骤8 对所有可见的状态x利用值函数式（2）得到完整策略。

步骤9 根据步骤8获得的学习策略得到支付值，形成支付矩阵Ut。

步骤10 由步骤9 得到的t时刻的支付矩阵Ut求取其纳什均衡解，得到t时刻的较优走步策略。

步骤11 执行算法2 虚拟行动方法找到协作追捕的最优解。

步骤12 执行走步策略，追捕成功，返回步骤3。

上述的算法流程如图3 所示，可以更加清晰直观地展示本文所提出的追捕算法。

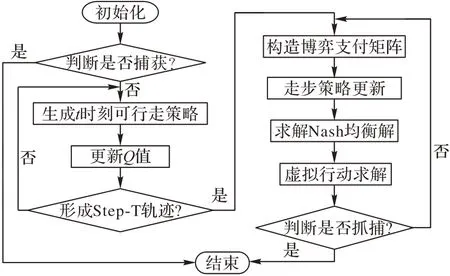
图3 多Agent追捕单目标猎物流程Fig.3 Flowchart of multi-agent pursuit single-target prey

3 实验仿真与结果分析

为了充分验证本文算法的有效性和合理性，将具有针对性的三种算法（文献［14］算法、文献［9］算法、文献［11］算法）与本文算法进行仿真实验对比，结果如表1 所示。实验的仿真环境为一个具有多处不同大小障碍物（房屋、人、山、河流等）的实验平台，环境中有三个追捕者、一个逃跑者。

假设所有的Agent具有以下特质：

1）追捕过程中所有的Agent 均只能活动在具有边界的地形中，其运动可选择的方向为360°。

2）所有的Agent 对环境中的障碍物以及每个Agent 等位置信息已知，并且所有的Agent 在环境中初始位置随机，初始化所有参与追捕者的速度值均为2 m/s，追捕者在速度上比逃跑者的速度要快，其追捕者的速度变化要根据速度影响系数KV变化。

3）假设当前时刻t是追捕者所占据的位置Xa，b(0 m ＜a＜720 m，0 m ＜b＜720 m)，追捕者与逃跑者每次移动一个身位（自身的宽度20 cm）*V（速度），其移动的方向选择为360°。用Hi(t)表示此时Xa，b处的Agent 可以运动到的位置，如式（14）所示：

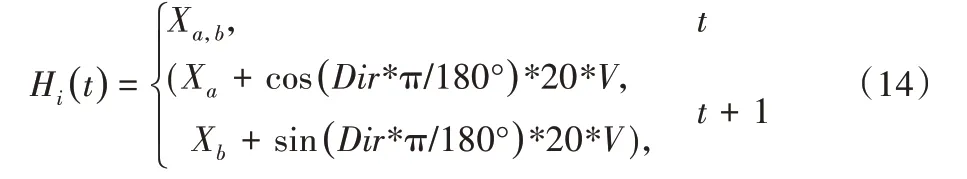
其中：Xa，b表示t时刻所在的位置；(Xa+cos(Dir*π/180°)*20*V，Xb+sin(Dir*π/180°)*20*V）表示在t+1 时刻所在的位置；Dir为转向度数，并且规定转向度数一次为5°；π=3.14；20 为追捕者以及逃跑者的身长；V为速度值。

在上述同样的环境中进行基于博弈方法的多Agent 追捕［14］、基于强化学习的多Agent 追捕［9］、基于自组织结构的多Agent 追捕［11］，以及本文提出的基于博弈论及Q 学习的多Agent 协作追捕等算法的研究。每种算法实验50 次，不同算法的追捕时间如表1 所示，表中数字代表追捕者从开始追捕逃跑者到完成追捕所用的时间。从表1 中可以看出，本文算法的协作追捕效率更高。

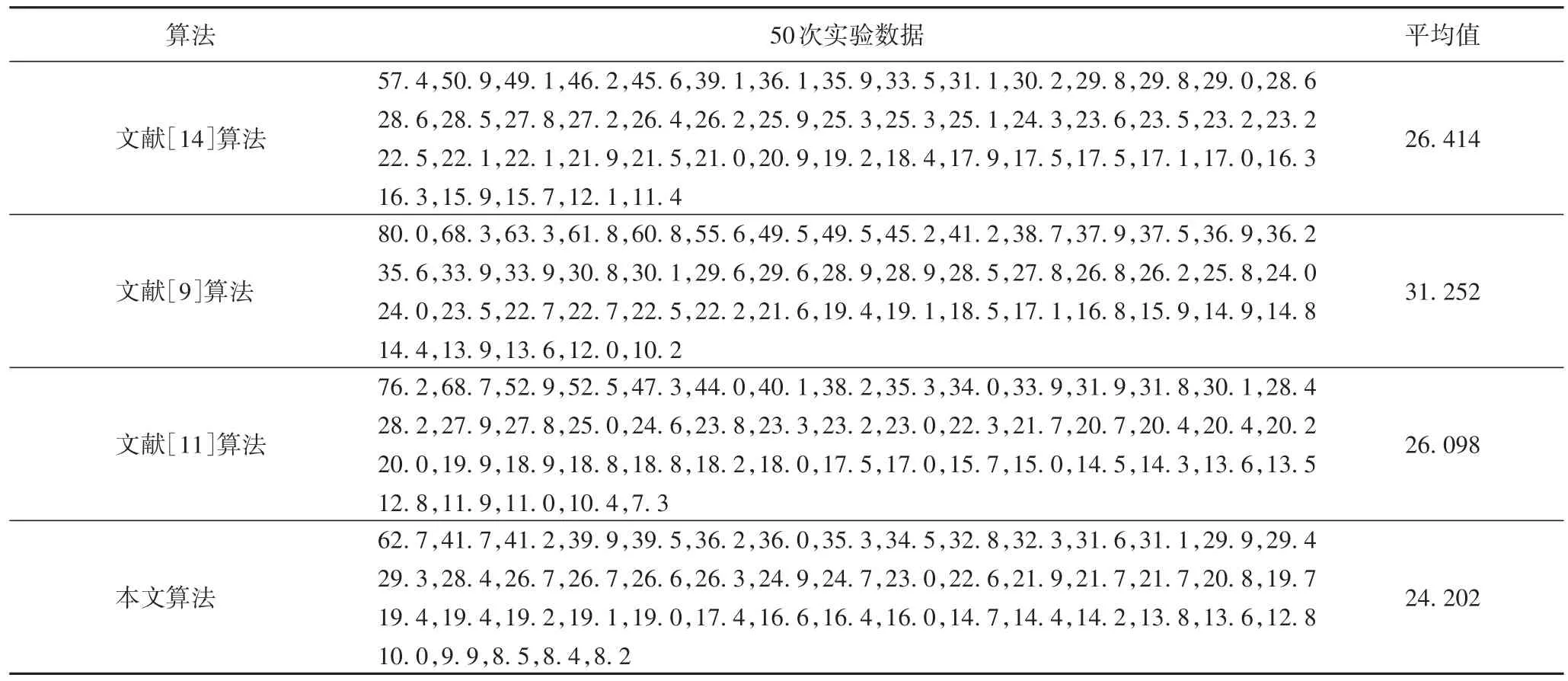
表1 不同算法的追捕时间对比单位：sTab.1 Pursuit time comparison of different algorithmsunit：s

在图4具有障碍物的环境中，多Agent追捕团队从初始位置开始，在人工势场合力的影响下，通过学习逃跑者的逃跑路径形成Step-T 策略，求解协作追捕博弈，得到Nash 均衡解，Agent 选择均衡策略进行围捕。从整个追捕的时间上可以得出，本文算法较优，且较为稳定。由图4（a）中可知，环境中的障碍物可以作为围捕逃跑者的有利条件；而图4（b）中为追捕团队不利用障碍物进行的围捕。

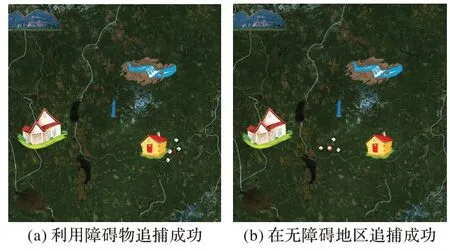
图4 多Agent追捕环境Fig.4 Multi-agent pursuit environment

在图5 中，利用不同的曲线展示了追捕团队从任务开始到任务结束的一个动态过程，仿真实验环境中设定环境的边界为X、Y，其中，0 m ≤X≤720 m，0 m ≤Y≤720 m。

图5（a）是利用文献［14］中博弈论的算法在本文实验平台中进行的追捕，图5（b）是利用文献［9］中学习的算法在本文实验平台中完成的追捕，图5（c）是利用文献［11］中自组织算法在本文实验平台中完成的追捕，图5（d）是本文所提出的基于博弈论和Q 学习的协作追捕算法在实验平台中完成的追捕。从图5 中可以看出：追捕者在前半段发现逃跑者之后都尽可能地去贴近逃跑者，速度变化根据式（7）动态改变；在后半段中，其包围系数KC会变得比较重要，可以直观地看出图5（d）中后半段的追捕完成的效率较高。

图6 通过实验验证本文所提出的算法3 即基于博弈论和Q 学习的协作追捕算法在同等环境下，支付函数权重值的不同对追捕效率的影响。使用随机的策略进行了15 次实验，分别每次改变两种参数。同时依据图5 中的追捕模拟运动轨迹可知，在前半段进行的贴近逃跑者运动中，速度影响的因素KV极为重要，在形成围捕之势时，包围系数KC的重要性就显示出来了。从图6 结果中可以看出，在同等环境下距离、包围程度，以及速度的权重不同，会使追捕的效率产生较大差异。

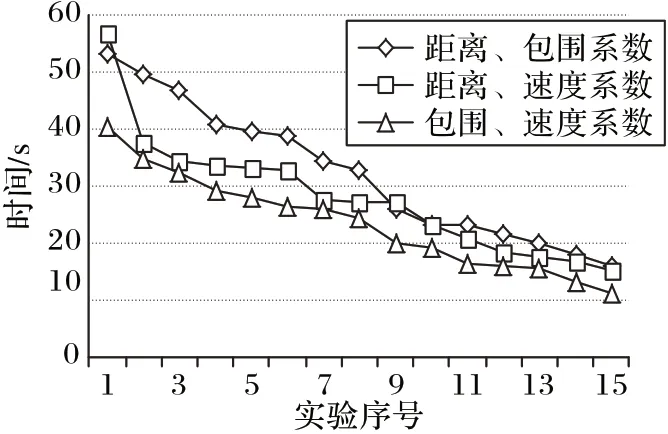
图6 同等条件下不同权值追捕时间对比Fig.6 Comparison of pursuit time with different weights under same condition

4 结语

本文提出了一种基于博弈论及Q 学习的多Agent 协作追捕算法，考虑到Agent 具有的学习能力，在追捕过程追捕者与逃跑者会因为策略选择相互影响。首先，利用博弈的相关模型建立协作追捕团队；其次，在追捕过程中随机选择已经成功的追捕案例，将逃跑者的逃跑路径进行切段划分总结，对逃跑者的运动路径进行有限次的学习，更新状态值，调整追捕者的可执行策略集；最后，求解协作博弈模型，追捕者选择较优的追捕行动策略并完成追捕，增强了博弈方法的环境适应性。同时，加入了虚拟行动行为选择算法，在出现有多个Nash 均衡的情况下，使得Agent 能够选择最优的均衡策略。仿真实验验证了所提算法既能快速捕获逃跑者和避开障碍物，又能适应当前的环境。在未来的研究中，将进一步研究存在多个逃跑者和多个追捕团队的协作追捕问题。