变式引导，提出问题

赖启茂

关键词：变式;提出问题;最短路径

中图分类号：G633.6    文献标识码：B    文章编号：1009-010X（2020）11-0062-03

爱因斯坦曾经说过：“提出一个问题往往比解决一个问题更重要。因为解决问题也许仅是一个数学上或实验上的技能而已，而提出新的问题，却需要有创造性的想象力，而且标志着科学的真正进步”。笔者在一次县级教研活动中专门开设“以最短路径为例，适时导引，提出问题”的公开课，整堂课围绕让学生能提出问题展开教学，获得多数教师的好评，也有教师反映这种模式很难操作。现把教学实录呈现给大家，欢迎同仁们商榷指正。

一、教学实录

师：同学们，平常上课，一般都是老师展示题目，同学们解答。如解答错误，老师再讲评。这种方式，同学们只能学会解决现有的问题。但是，现代社会迫切需要创新意识和创新能力的人才。这就需要同学们在日常学习中学会提出问题，提出与别人不一样的问题，提出有思考价值的问题。这节课，我们就尝试一下，以最短路径为例，只提出问题，先不解答。

师：一说到最短，同学们能想到什么？

生众：两点之间，线段最短。垂线段最短。

师：对，这是说，点与点之间，线段最短;点与直线间，垂线段最短。

师：今天，就以这两个知识点为基础，不断变式，提出新问题。

情景1：如图1，A、B表示两个村庄，l表示一公路，现欲在公路上修建一个加油站，从路径的角度，你能提出什么问题？

生1：在公路l上哪一点建，到两个村庄的距离相等？

师：好，你是从公平公正的角度提出问题的。

生2：在公路l上哪一点建，到两个村庄的路径之和最短？

师：不错，生2是从最短路径的角度提出问题。

师：接下来，同学们思考，对图1进行适当变化，又可以提出什么问题？

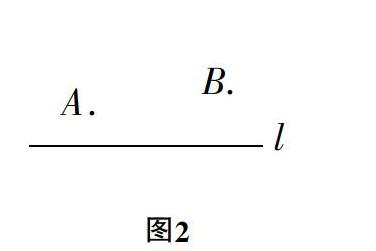
生3：刚才，A、B在l的异侧。如果A、B在直线l的同一侧，如图2

那么，①直线l哪一点到A、B的距离相等？

②在直线l上哪一点到A、B的路径之和最短？

师：生3的数学思维不错，能从A、B在l的异侧想到A、B在l同侧，然后提出两个很有思考性的问题。

就图2的情况，还能提出什么问题吗？

（生众沉默）

师：刚才生3提出，在直线l上哪一点到A、B的路径之和最短，你可以改变其中的某个因素，从而可以提出不同的问题？

生4：想到了，想到了，可以问：

①在直线l上哪一点到A、B的路径之和最长？

②在直线l上哪一点到A、B的路径之差最长？

师：很好！看得出我们的同学更能提出问题了。生4怎么提问的呢？由“和”想到“差”，由“短”想到“长”。这叫逆向思维，即朝相反的方向去考虑，可提出新的问题。这里要提醒的是，生4提出的①中“路径之和最长”，同学们想想，现实生活中，有没有选择更长的路径去走的？这好象不太合乎常理，通常人们考虑的是怎样走最短。因此，从思考的角度而言，可以在各方面去提出问题，但是提出的问题要有现实意义的为好，这样的问题更有思考和应用的价值。现在来说说生4提出的问题②中，“路径之差最长”，这问题耐人寻思，思维含金量很高。同学们课后好好研究研究。

生5（急不可耐的样子）：還可以问：在直线l 上哪一点到A、B的路径之差最短？

生4（迅速回答）：那不是0嘛，显而已见。

师：生5能从“路径之差最长”想到“路径之差最短”也了不起！好，情景1就先提问到这里。

现在，把图1进行变式，一条直线变成二条直线。

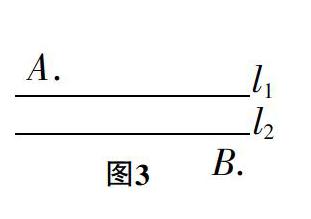
情景2：如图3，l1、l2 之间表示一条河，A、B两个村庄分别在河两岸，现在想在河上建一座桥。

同学们想想，可提出什么问题？

生6：在哪里建桥，才能使得A到B的路径最短？

师：很有道理，人们关心的是哪里建桥，A、B两地的人们互相往来的路径更短。

在图3中还能提出新问题吗？

（生众沉默）

师：这里，A与B之间有一条河，你能想到什么？

生7：如果有两条河呢？如图4两条河上分别在哪里建桥，才能使A到B的路径之和最短？

师：帮生7补充一下，假定这两条河是平行的，那么生7的问题是个好问题，很有思考性。

生8：我也补充一下，假定两条河不平行，如图5，那么在两条河上哪里建桥，才能使A到B的路径之和最短？

师：对，由“平行”想到“不平行”又提出一个新颖且有难度的问题，对我们的大脑很有挑战性。接着我们把图1，再次变式，直线变成折线。

情景3，如图6，OA，OB表示某地的两条街道，点P是邮局，现在想在OA、OB分别建一个报刊投递点。就邮递员的路径可提出什么问题？

生9：分别在OA、OB上哪一点作报刊投递点，才能使邮递员从邮局出发到OA中的投递点M，然后到OB中的投递点N，再回到邮局P所走的路径之和最短？

师：好样的，提出一个三线段之和最短的问题。从情景3中抽象出几何问题是：点P在∠AOB内，在∠AOB两边上如何分别确定点M、点N，使△PMN的周长最短，很有思考性的问题。在此基础上，还能提出怎样的问题？

生10：可否提出一个四边形周长之和最短的问题？

师：行呀，怎样表达呢？大家想想。

生10：四边形应有四个顶点，OA上一点，OB上一点，还有P点，说明∠AOB内还需一个点。这样就可提出一个问题：已知如图7∠AOB，和∠AOB内的两点P、Q，在OA、OB上分别确定点M、N，使四边形PMNQ的周长最短。

师：精彩！又一个典型的问题。最后，把图6进行变式，把角的开口封闭，∠AOB变式为△ABC.

如图8，△ABC内找一个点P，路径的角度，可提出什么问题？

生11：如何确定点P，使它到三个顶点的距离相等。

生12：（忽有所悟）：如何确定点P，使它到三边的距离相等。

师：很棒，两个很有意义的问题。类比前面的几个问题，还可提出什么问题？

生13：①如何确定点P，使PA+PB+PC最短。

②如何确定点P，使它到三边距离之和最短。

师：问得好！今天的提出问题就到这里。同学们提出的各种问题，就作为今天的作业回去思考，下节课再来交流。现在一起回顾一下，这节课，我们是怎样不断变式提出问题的？

生：（略）

二、教学反思

（一）设置情景，催生学生的提问欲望

所有问题的提出，都有其特定的背景，因此，希望学生提出问题，教师得先围绕某个主题，设置相应情景。比如情景1，公路两旁分别有一个村庄，公路上要建加油站，从路径角度提出问题。此情景一出现，绝大部分学生都能“触景生情”提出问题。后面情景2，情景3、情景4都是学生身边的事例，如果学生用数学的眼光去观察、思考，不难产生提问的欲望。

设置情景的原则：①应在学生的生活经验和认知水平范围内设置情景，学生才可能有“感”而“问”;②情景中出现的各个要素应恰当，过少或过多都不利于学生提出问题，如果过少，比如情景1中，缺少从“路径角度”，学生要么茫然，要么胡思乱问，如果过多，比如情景1中，改为“从距离相等的角度提问”，整个情景无问题可提了。

（二）变式导引，积累学生的提问方法

怎样才能提出问题，与学生的原有的知识结构、思维品质、提问方法等多方面因素有关系。作为教师，普遍十分重视帮学生夯实基础知识，努力提升学生思维品质。然仅此而已，学生还不会提出问题。因此在日常教学中，教师要树立培养学生问题意识的意识，引导学生经历、感悟提出问题的过程与方法。当然，提出问题有很多方法，教师应循序渐进地渗透。可从“变式提问”入手，让学生充分感知如何面对情景或数学现实提出问题。本节课，情景1中，A、B两点从异侧变同侧;情景2中，一条河变两条河;两条河平行变不平行;情景3中，三角形变四边形;情景4中，开放变封闭。诸如此类的变式，都是在导引学生怎样改变角度，提出问题。长此以往，学生的问题意识越来越强烈，逐渐地把提出问题内化为自己主动学习的一种习惯。

（三）赏识鼓励，增强学生的提问自信

我们中国的学生，大多数习惯于解题。如果让他们“无中生有”提出问题，普遍感到很困难。因为提出问题与解题是不同角度、不同层次的思考，是属于更高阶思维的体现。开始时学生对提出问题都很畏惧。因此，教学中除了设置学生熟悉的低起点便于学生发问的情景外，教师还需特别注重赏识鼓励学生。学生提问时可能出现多种现象，如：①提不出问题;②提出的问题可能没意义;③表达不清楚等等，每个细节教师都要从学生的心理感受方面着想，辅之以合适的鼓励，扫清学生提问路时的心理障碍。逐步使学生增强提出问题的自信，从敢于提问向善于提问迈进。

参考文献：

[1]刘湘萍.论数学课堂中提问的方式與技巧[J].中学数学，2019，（6）.

[2]温建红.论数学课堂预设提问的策略[J].数学教育学报，2011，（3）.