差分粒子群算法在PUMA机器人逆运动学求解中的应用

汪院林 袁锐波 袁安华

摘要：传统逆运动学求解主要从逆运动学方程出发，基于一定的数学理论推导，不能完全实现计算机程序化，且精度与计算效率较低：为改善这一缺陷，基于机器人正向运动学方程，借助MATLAB工具，使用蒙特卡洛法仿真分析出PUMA560机器人的工作空间，任取一点末端执行器位姿作为逆运动学求解的已知位姿矩阵T，结合差分粒子群仿生智能算法作为逆运动学求解的主要理论算法。将计算出的旋转关节变量θ1-θ6代入正运动学方程，得出末端位姿矩阵于;通过计算分析T与于相关角度误差，两矩阵所对应的位置向量与姿态向量误差精度为0.001数量级，完全满足目前机器人定位要求。基于差分粒子群理论的机器人逆运动学求解方法计算收敛速度更快，能高度实现计算机程序化，误差精度高，提高计算效率。

关键词：正运动学;差分粒子群算法;收敛速度;位姿矩阵;逆运动学解

DOI： 10. 11907/rjdk.191724

开放科学（资源服务）标识码（OSID）：

中图分类号：TP319

文献标识码：A

文章编号：1672-7800（2020）004-0203-05

0 引言

近年来，机器人技术发展迅速，在工业等领域占据重要地位，机器人运动学研究也日益增多。机器人运动学主要由正运动学与逆运动学两部分组成：机器人正运动学主要以基坐标为基础，根据各关节旋转角度确定末端执行器的位姿;逆运动学与其相反，以末端关节为出发点最终回到基坐标。正运动学由多个关节的位姿矩阵进行连乘运算，最终确定末端执行器唯一的位姿矩阵，而逆运动学末端位姿可以对应机器人系统关节的多个解[1]。机器人逆运动学问题随着运动关节的增多而更加复杂，它实质上是解一个非线性方程问题。实际应用中，机器人所要执行的任务通常用其基坐标系描述[2]。因此，机器人逆运动学求解在控制领域显得尤为重要。

目前，机器人逆运动方程求解方法主要有解析法、几何法、迭代法、几何一解析法[3]等。Paul等[4]对PUMA机器人提出了当d6=0时逆运动的解析解;Lee等[5]提出应用几何学方法求解各关节变量;王奇志等[6]提出当d6≠0时的一种解析解法;戴齐等[2]对PUMA机器人逆运动解利用几何一解析法进行研究。基于传统理论方法虽然模型建立简单，但计算效率低下，难于析出机器人逆运动学的所有解，且计算机程序的可移植性较差;吴振宇等[7]利用遗传粒子群算法在解决非线性问题时的优势，对PUMA机器人的逆运动解提出遗传粒子群算法理论，但该方法需要大量的样本数据进行训练，且对目标函数进行最优搜索时收敛速度较慢，会陷入局部最优状态，存在一定不足。

本文提出一种新的逆运动求解方法：基于差分进化算法（ Differential Evolution Algorithm.DE），该方法结构简单，收敛速度快，鲁棒性较强，是与粒子群优化算法（ ParticleSwarm Optimization，PSO）同时考虑位置与速度两个参数相结合的一种混合智能算法[8]。从正向运动学方程出发，在各关节角变量范围内取出相应角度值，建立PUMA机器人工作空间范围模型。通过图像方式验证三维空间尺寸是否与机器人结构尺寸一致，图形各投影平面中有没有明显的空洞现象。基于所有末端执行器位姿点，取其中某一点位姿，将差分粒子群混合算法作为PUMA机器人逆运动求解主要理论，弥补了传统逆运动求解方法的不足，提高了计算效率和精度。

1 正运动学模型

1.1 D-H法坐标系及几何参数

PUMA型机器人有6个自由度，且6个关节均为旋转类型，可采用标准D-H法建立杆件坐标系描述各关节之间的特征参数和运动关系。该矩阵为4x4的齐次变换矩阵，通过该矩阵可得出与PUMA560机器人几何尺寸相关的运动学方程。标准D-H法得到的相邻杆件之间的齐次变换矩阵如下：

各连杆几何参数如表1所示。

1.2 运動学方程

PUMA560机器人由多个旋转关节组成，其中包含旋转基座、大小臂、手腕等几部分[9]。前3个关节用于对末端执行器进行定位，后3个关节主要用于保证末端执行器的姿态。PUMA机器人运动学正解方程如下：

若给出关节旋转角及各连杆几何参数，通过式（2）可求出PUMA机器人末端执行器位姿;若仅已知末端关节位姿，则需要确定中间各关节旋转角，这需要进行大量计算方可求出。

2 PUMA机器人工作空间仿真

2.1 蒙特卡洛法工作空间分析

目前，确定机器人工作空间的方法主要有数值法、解析法及图解法。图解法方法较简单，但受关节数目限制，对多自由度机器人进行工作空间分析时需采用分组处理[10];解析法主要采用微分几何学原理，通过绘制函数解析式的多次包络曲线确定工作空间，表示复杂，多用于三自由度以下机器人的工作空间分析[11];数值法多建立在极值理论及相关优化理论之上，通常计算量庞大，用于图形边界为曲面且凹陷时，计算可靠性低[12]。本文提出一种建立于数值法基础上且引进随机分布方法的蒙特卡洛法，它主要依托随机抽样的数学理论将工程问题转化为数学模型，应用范围较广。在工程中，主要用于一些随机无规律性的物理问题，而在机器人领域多用来进行误差分析。然而，机器人工作空间的仿真计算也能通过蒙特卡洛法理论完成，可利用计算机辅助计算[13]。

蒙特卡洛法求解机器人工作空间，主要是在机器人各关节的旋转变量范围内按一定步长随机取值，然后把各旋转关节的取值代入方程式（2）中，最终计算出自由端执行器的空间坐标值，而末端关节所有随机值的集合则构成机器人工作空间。将末端执行器得到的坐标点输出到图形设备上，可得出机器人工作空间的三维仿真图形。

蒙特卡洛法主要步骤如下[14]：

（5）设定所需要输出的点集数，通过循环方式重复步骤（3）、步骤（4），直到满足条件为止。

上述算法可借助MATLAB软件程序化完成，最终将末端位置空间点通过三维绘图函数plot3输出。利用蒙特卡洛法进行机器人工作空间仿真步骤如圖2所示。

2.2 PUMA560机器人工作空间仿真分析

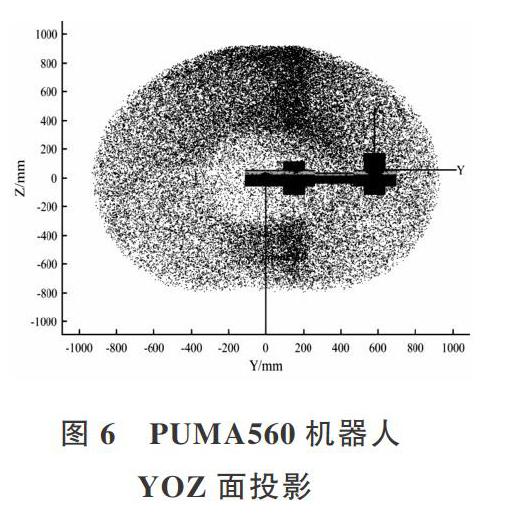
根据机器人运动学正解方程及蒙特卡洛法理论，将该算法编写成MATLAB程序进行仿真分析。PUMA560机器人各关节角度取值点为50 000个，最终输出50 000个点作为三维工作空间，仿真结果如图3-图6所示。

从以上三维工作空间仿真图及各平面投影图分析可得出：仿真分析出的工作空间均未超出各关节变量旋转范围，且各图形尺寸范围与PUMA560机器人结构尺寸相一致。从图中看出各点集均匀，未出现空洞等现象。因此，该仿真结果与实际相符。

3 逆运动学求解

粒子群优化算法（PSO）是来源于观察鸟群觅食而诞生的一种仿生算法，广泛应用于非线性问题、多极值和不可微等场合的优化，需要设置的参数较少[16]。PSO算法在搜索空间范围内寻找最优解，主要与粒子适应度和群体两个参数有关，而粒子群的每一个体可表示某优化问题的一个概率解。每个粒子主要由速度和位置两大属性决定。粒子适应度是将粒子位置代入目标函数得到的数值，粒子适应度是判断粒子优劣的标准。在对问题进行搜索迭代时，粒子主要依据两个参数作出变换：①粒子受自身经验影响而得到的最优解，即个体历史极值pBest;②粒子受全局影响而寻到的最优解，即全局历史极值gBest。用以下公式对粒子位置及速度进行更新。

式中，v（t+1）、x（t+1）分别为下一时刻粒子的速度与位置;C1、c2为学习因子，代表个体经验与群体经验对粒子速度影响所占权重;rand（）为随机数，范围为[0，1];ω为惯性权重，是与时间有关的动态调整参数。ω取值对算法影响至关重要，ω较大能提高全局搜索能力，但收敛速度很慢，较小则易陷入局部搜索。本文对ω的取值随迭代次数从0.9线性递减为0.4[17]，变化公式如下：

差分进化算法（DE）是一种并行求解的进化算法，与遗传算法类似，用相同的算术操作（如：变异、交叉和选择算子）对初始群体或父代群体进行更新。DE首先进行变异操作，在搜索范围内任意选取一个体作为基准父代个体，并在父代个体外随机选取两个向量进行差值计算，加权后与父代个体求和;然后经交叉算子在父代个体与变异个体间进行选择，产生实验个体;最终结合目标函数对父代个体和实验个体作选择，生成新的子代个体[18]。

其中，F（x）为对应问题的目标函数值。

本文根据PUMA560机器人逆运动学方程建立数学模型（目标函数）：机器人末端执行器位姿矩阵为T，利用差分粒子群算法优化得出第t次搜索时各关节变量所对应的矩阵T，数学模型可表达为两矩阵T与T之间的空间距离，使其为极小佰，计算如下：

本文结合DE与PSO各自的优点，提出一种差分粒子群算法（DEPSO），用于解决PUMA560机器人运动学问题。该算法以PSO流程为主，通过DE算法增强了粒子群体的多样性，可避免PSO算法陷入局部最优解。DEPSO算法步骤如下：①在粒子群体范围内，初始化粒子位置与速度，设计数器t=0;②计算粒子适应度，用于DE算法选择粒子，计数器t=t+1;③粒子根据式（8）进行DE变异操作并作选择;④更新局部最优解pBest与全局最优解，根据式（5）.式（6）计算粒子位置与速度;⑤粒子根据式（9）进行DE交叉计算;⑥计算粒子适应度;⑦选择新一代粒子;⑧更新局部最优解和全局最优解;⑨若计数器大于给定循环次数，则退出计算，否则，调至步骤②。

DEPSO算法基本流程如图7所示。

4 实验结果与分析

PUMA560机器人各杆件参数如表1所示。根据蒙特卡洛法机器人正运动学求出所有末端关节位姿矩阵，任取其中一点作为逆运动学求解的末端位姿矩阵T，如下所示：

根据矩阵T与于，可从位置与姿态矩阵分析求解精度。实验末端关节矩阵T对应的位置坐标为[ 600.227，622.914，164.221];关节变量θ1-θ6所对应矩阵T的位置坐标为[600.2283，622.9124，164.2217]，计算得出T与于之间的误差精度为0.001mm数量级。

姿态矩阵所对应角度为T和于各自的反余弦值[20]。对T与于进行分析可得出：PUMA560机器人指定末端位姿矩阵法向向量各自的方向角[106.5334°，76.3895°，21.6705°]，所求关节角对应位姿矩阵的法向向量方向角为[106.5313°，76.3855°，21.6714°];机器人指定末端位姿矩阵滑动向量方向角为[61.0559°，143.2778°，69.4417°]，所求关节角对应的位姿矩阵滑动向量方向角为[61.0585°，143.2788°，69.4397°];PUMA560机器人指定末端位姿矩阵所对应的接近向量方向角各自为[34.1543°，56.6547°，83.4417°]，所求关节角对应位姿矩阵的接近向量方向角各自为[34.1507°，56.6577°，83.4445°】。通过以上计算可看出，利用差分粒子群算法计算PUMA560机器人得出的关节变量所对应的末端姿态矩阵与指定末端姿态矩阵的误差精度在0.001°数量级，由此可知，将本文的差分粒子群算法用于求解PUMA560机器人逆运动学求解完全满足定位精度要求。

5 结语

本文从正运动学方程出发，根据蒙特卡洛法求解出PUMA560机器人工作空间的末端关节位姿矩阵，任取一点用于逆运动学求解过程。结合差分优化算法与粒子群算法优点，提出一种差分粒子群混合智能算法，将其作为逆运动学求解方法。该方法与其它传统逆运动学求解方法相比较，更适合于计算机计算，具有定位精度高、收敛速度快、计算高效等优点。通过实例验证可知，该方法用于机器人逆运动求解问题满足当前机器人定位误差要求，是智能算法与逆运动数值法相结合的新理论。

参考文献：

[1]JOHN J，CRAIG.机器人学导论[M].以，贠超，译.北京：机械工业出版社.2006.

[2] 戴齊，姚先启.一种求解PUMA机械手运动学逆问题的分解法[J].西南交通大学学报，1989（4）：30-35.

[3] 陈宁，焦恩璋.PUMA机械手逆运动方程求解新方法[J].南京林业大学学报（自然科学版），2003，27（4）：23-26.

[4]PAUL R P.Robot manipulators： mathematics， programming and con-trol： the computer control of robot manipulators[M].Cambridge： MITPress.1981.

[5] FU K S，CONZALEZ R C，LEE C S G.Robotics： control， sensing，vision and intelligence [J]. Me Graw-Hill. 1987（6）：78-82.

[6] 王奇志，徐心和，尹朝万.PUMA机械手逆运动方程新的推导方法及求解[J].机器人，1998，20（2）：81-87.

[7]吴振宇，姚明江，冯林，等.基于遗传粒子群的PUMA机器人逆运动求解[J].计算机仿真，2011，28（ 10）：173-176.

[8]池元成，方杰，蔡国飙.基于差分进化和粒子群优化算法的混合优化算法[J].计算机工程与设计，2009.30（ 12）：641-647.

[9] 布鲁诺·西西里安诺.机器人学：建模、规划与控制[M].张国良，译.西安：西安交通大学出版社，2013.

[10]蔡蒂，谢存禧，张铁，等.基于蒙特卡洛法的喷涂机器人工作空间分析及仿真[J].机械设计与制造，2009（3）：161-162.

[11] KOHLI D. HSU M S.The jacobian analysis of workspaces of mechan-ical manipulators[J]. Mechanism& Machine Theory， 1987， 22（3）：265-275.

[12]赵燕江，张永德，姜金刚.基于Matlah的机器人工作空间求解方法[J].机械科学与技术，2009，28（12）：1657-1661.

[13] RASTEGAR J，PEREL D.Ceneration of manipulator workspaceboundary geometry using the monte carlo method and interactive com-puter graphics[J]. Journal of mechanical design， 1990， 112 （3）：452-454.

[14] 郭明，周国斌.多关节机器人工作空间的分析与评价方法[J].机器人，1988，10 （4）：7-12.

[15] 沙漠，邓子龙.基于MATLAB对于PUMA560机器人的运动空间分析研究[J].机械制造与自动化，2016，45（2）：156-159.

[16] KAO Y T，ZAHARA E.A hybrid genetic algorithm and particleswarm optimization for multimodal functions[J]. Applied Soft Com-puting Journal， 2008.8 （2）： 849-857.

[17] 王志，胡小兵，何雪海.一种新的差分与粒子群算法的混合算法[J].计算机工程与应用，2012，48（6）：46-48.

[18] 栾丽君，谭立静，牛奔.一种基于粒子群优化算法和差分进化算法的新型混合全局优化算法[J].信息与控制，2007，36（6）： 708-714.

[19]谢宏，禹文科，杨鹏，等，多子群分层差分粒子群算法的逆运动求解方法[J].电子测量与仪器学报，2015，29（10）：95-99.

[20] 芮梃.PUMA机器人逆运动模拟退火粒子群求解方法[J].计算机工程与应用，2010，46（3）：27-29.

（责任编辑：杜能钢）

作者简介：汪院林（1994-），男，昆明理工大学机电工程学院硕士研究生，研究方向为流体传动与控制;袁锐波（1968-），男，博士，昆明理工大学机电工程学院教授，研究方向为电液比例伺服控制、复杂机电系统集成与控制;袁安华（1991-），男，昆明理工大学机电工程学院硕士研究生，研究方向为流体传动与控制。本文通讯作者：袁锐波。