基于贝叶斯推断的多层软测量建模在丁醇发酵中的应用
2020-06-19朱湘临顾雯炜王博
朱湘临 顾雯炜 王博

摘要:针对丁醇生产过程中发酵产物品质参量难以实时测量,现有测量方法精度不高、测量结果受不确定因素影响较大的问题,提出一种基于贝叶斯推断和支持向量回归( Support vector machine regression,SVR)的多层软测量建模方法。首先应用贝叶斯推断计算后验概率、筛选偏置数据,并对偏置数据校准,建立第一层SVR模型:然后利用贝叶斯推断进行二次校准,建立第二层SVR模型,对第一层SVR模型输出进行修正,得到最终预测结果,克服干扰和偏差引起的模型不准确问题。将基于贝叶斯推断的多层支持向量回归( Bi-SVR)预测模型应用于丁醇发酵过程,仿真及实验结果表明,相较于传统SVR预测模型,系统在低干扰的情况下预测精度提高了4.52%,在高干扰时预测精度提高了5.37%。
关键词:微生物发酵;贝叶斯推断;支持向量机回归;软测量
中图分类号:TP319
文献标识码:A
文章编号:1672-7800( 2020)004-0183-06
0 引言
随着科技的进步,各国能源开采和研究逐渐转向可再生方向,生物能源以其可再生和低污染等优点成为现代能源研究的热点。乙醇是美国石油危机以来最先进行研究的生物燃料,经过长期研究发现,和乙醇相比,丁醇具有更高的能量密度和燃烧值,能够以任意比例和汽油混合使用,并且原有燃机不需要作任何改动就可直接使用,拥有广阔的研究前景[1]。但是丁醇发酵过程复杂,涉及许多生物量,实现丁醇工业化生产需要克服其在线精准测量难题。
基于过程数据和预测能力的软测量技术因其良好的测量能力得到学术界和工业界的关注[2]。软测量方法可以归结为两种:①基于生物机理进行建模;②基于历史数据驱动进行建模。前一种方法需要基于生物机理知识开发模型,这些模型用于阐明过程与结果这两个变量之间复杂的物理、化学或生物关系[3]。因此基于机理知识的软测量建模需要耗费很大的精力在机理研究上,极易影响软测量建模的准确性。因此,仅取决于历史数据的数据驱动软测量技术更有研究和发展前景[4]。
早期软测量技术的数据驱动建模方法集中于多元统计技术,例如偏最小二乘法( Partial least squares,PLS)。这类方法可以处理变量的共线性,但是PLS本质上是线性模型,不能处理非线性过程,除非内核函数等特定的非线性变化被整合[5]。人工神经网络( Artificial neural networks,ANNs)已应用于构建非线性过程的软测量模型。一些学者研究将神经网络与PLS等多元统计技术结合用于非线性系统的软测量技术[6]。利用人工神经网络模拟过程中的非线性关系,PLS用来处理测量数据的共线性以及替换缺失值问题[7]。尽管ANN技术已被证明能够处理系统非线性和代表过程知识,但其需要庞大的数据库支撑,因此所训练的一般模型预测效果较差。另外,神经网络也可能会收敛到局部最小值,从而影响软测量结果的准确性[8]。
独立分量分析(Independent component analysis,ICA)和支持向量机( Support Vector Machines,SVM)也应用于软测量技术开发。ICA可基于高阶统计量提取相互独立的分量,并识别传统PLS方法无法处理的非高斯过程特征[9]。现有的一些软测量建模方法没有充分考虑到实际生产中可能产生的不确定情况,包括缺失值、外部干扰所导致的测量误差和漂移、样本延迟和数据长度不规则等[10-11]。贝叶斯推断作为处理系统不确定性的强大概率技术已经引起人们对过程系统各个领域的兴趣,包括软测量建模[12-13]。Yan等[14]提出用贝叶斯推断法选择SVM模型参数值并优化软测量模型。之后有很多研究人员将贝叶斯推断与SVM相结合进行建模,取得了良好的预测效果[15]。
本文将支持向量回归与贝叶斯推断相结合,借鉴神经网络的深度学习方法思路进行多层建模,用于非线性生物丁醇发酵过程中的软测量开发。首先,在预处理步骤中展开和缩放多路数据矩阵;然后,将过程变量的测量数据用于贝叶斯推断,以此估计模型输入空间内所有样本的后验概率,对相应后验概率小于预定义置信水平的样本子集用贝叶斯标识和校准估算。将处理过的输入样本与第一层输出数据一起用于构建第一层支持向量回归模型。同样,用贝叶斯推断筛选在置信度界外的后验概率偏置数据;最后,由第一層预测模型的校准输入和输出数据进行拟合构建第二层SVR模型,得到准确的预测值。参数C的一组值。通过最小化平均根均值、多重交叉验证,最后确定C=10,;σ=1是最佳选择。
2 基于贝叶斯推断的多层软测量建模
为处理测量过程中可能出现的干扰、噪声、样本延迟和缺失值等问题,将贝叶斯推断与支持向量回归相结合,建立软测量预测模型。假设过程变量的多路输入数据矩阵是X(Ix Jx×L),输出矩阵是Y(/x Jy×L)。这里L表示批数,Jx和JY表示输入及输出变量的数目,L是每次发酵的观测数。首先,利用动态时间规整( Dynamic time warping,DTW)技术对齐和同步不等长度的输入数据;然后沿着每组变量列的不同采样时刻进行数据堆叠,将多路输入和输出数据矩阵展开成两维矩阵X(IL×Jx)和Y(IL×JY)[16-17],如图1所示。
利用贝叶斯推理对输入和输出测量进行校准,构造第二层SVR模型,并将修正的输入测量值反馈给该模型以预测最终输出。对于任何一组测量数据,需要计算在任意采样时刻,。上的同步数据向量的后验概率,从而确定数据不确定性的重要性。对于任何有偏差的测量,可以应用基于贝叶斯推理的数据校准,将校准数据向量作为输入直接发送到第二层SVR模型,以获得不同质量属性的预测。需要注意的是,第一层SVR模型仅是在训练阶段用于输出数据校准,而第二层SVR才是作为学习和预测的主要软测量模型。设计的贝叶斯推理方法能够处理不同类型测量的不确定性,包括缺失值、传感器偏差和漂移。与此同时,采用支持向量回归方法对过程变量和输出之间的非线性关系进行建模。
对基于贝叶斯推断的多层支持向量回归软测量建模方法总结如下:①分别为输入和输出变量形成两个多路训练数据矩阵x和v;②使用动态时间弯曲技术对齐和同步数据长度;③对多路输入和输出数据矩阵进行可变智能展开,并将它们转换成二维矩阵;④计算输入样本的后验概率。对于相应的后验概率小于显著性水平a%的样本标记为具有显著不确定性的有偏测量;⑤基于贝叶斯推理对偏置输入测量进行校准;⑥使用校准的输入数据连同原始输出样本建立第一层SVR模型;⑦利用来自第一层SVR模型的预测输出值,估计所有输出样本的后验概率,并使用与步骤④相同的统计规则识别偏差测量;⑧对偏差输出测度进行贝叶斯修正;⑨使用校准的输入和输出数据构建第二层SVR模型;⑩对于任何新的过程测量样本,计算同步输入向量的后验概率并确定其是否显著偏置;(11)偏置输入测量数据校正,实现基于贝叶斯推理;(12)将无偏置或校准的输入数据发送到第二层SVR模型,以获得相应的质量变量预测。
图2为该方法流程。
3 丁醇发酵多层软测量应用
现代计算机技术的迅猛发展为发酵生产智能化奠定了良好基础,准确和可靠的在线参数测量是不可或缺的环节,既可实时观测和记录生产数据,又可实现发酵生产中的精准控制。本文以丁醇发酵为例,应用多层软测量建模方法进行数据的预测实验,并与常规SVR方法下的预测结果进行比较分析。
3.1 丁醇发酵工艺
丁醇发酵不同于乙醇的“一步法”发酵,需要经过“两步法”:先将木质纤维水解再向水解液中加入拜氏梭菌进行发酵生产,在发酵过程中会产生有毒物质抑制发酵[18]。实验表明加入适量的碳酸钙可实现脱毒效果,同时加入适量丁酸能起到促进丁醇生产的作用。发酵罐是发酵过程中的主要设备,需要提供微生物生长必需的养分、水、空气和适宜的温度[19]。在该过程中分别通过操纵酸/碱和水温控制发酵罐中的pH值和温度。根据丁醇发酵工艺,酸碱平衡添加物分别为碳酸钙和丁酸控制发酵过程中的pH值。碳酸钙起到抑制剂作用,丁酸起到促进丁醇生产的作用[20]刚。丁醇发酵过程如图3所示。
在此过程中,选择生产丁醇的4个最关键浓度变量作为软传感器输出,其它6个测量变量用作输人[21],输入和输出变量分别标记为I1-16和O1-O3,如表1所示。
3.2 多层软测量预测结果比较
为形成训练数据集,随机取30次发酵数据,每次持续72小时。测试分为两次,每次添加不同的干扰以验证软测量模型性能。因为丁醇发酵具有非线性、时变性和多相特征等特点,所以本文采用RMSE指数评估软测量模型性能:
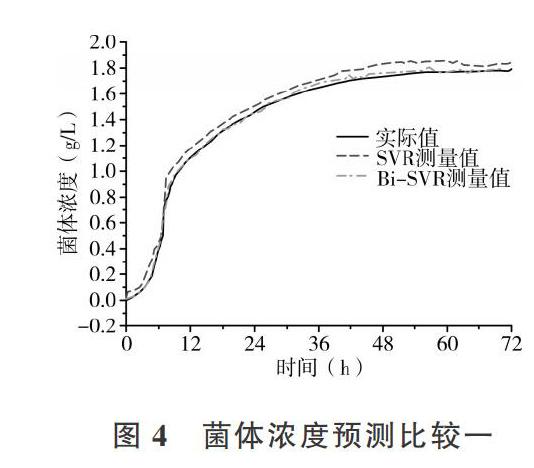
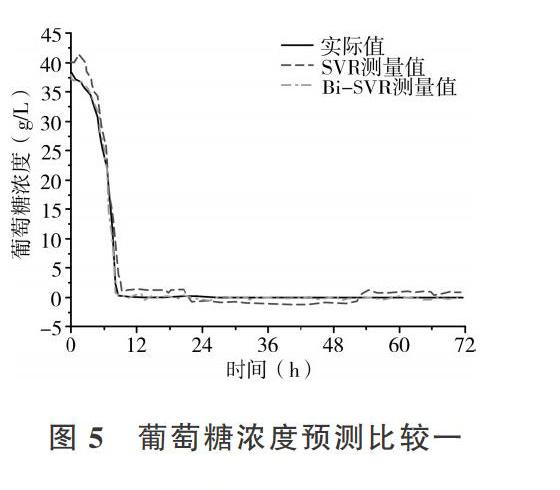
其中( )和( )分别是第,个输出变量的实际值与估计测量值。在低干扰情况下两种不同类型的软测量模型最终得到的预测结果如图4、图5和图6所示。
同时,对SVR和Bi-SVR方法的软测量建模及预测结果进行定量比较,见表3。
从软测量预测结果可以看出,在所有3个输出变量的预测精度方面,所提出的Bi-SVR方法优于传统的SVR方法。在图5中,SVR预测的菌体浓度与实际测量值有一定偏差,走势基本一致但是缺乏精度。相比之下,Bi-SR方法的预测与实际测量值的轨迹基本吻合,偏差较小。由表3可知,Bi-SVR方法训练和测试样本的RMSE指数值均小于SVR法,表明所提出的Bi-SVR方法能夠有效处理干扰问题并纠正偏置测量。传统的SVR方法会将偏置数据进行模型拟合从而导致模型的准确度下降。Bi-SVR方法可以利用贝叶斯推断刷新偏置数据,并对具有偏差的输入输出进行校准。对于图6中的葡萄糖浓度预测,SVR软传感器预测值与实际值偏差较大。相比之下,Bi-SVR方法在贝叶斯框架下具有最小的误差。图7中丁醇浓度的预测值在SVR和Bi-SVR方法下初期表现相差不大。当干扰出现时预测结果会出现波动,偏离实际值。可以看出,除了利用贝叶斯推断进行偏置数据的校正之外,在贝叶斯框架中还保留了支持向量回归机的固有泛化能力。
为了进一步验证Bi-SVR方法在具有偏差测量数据下的性能,在第二个测试样本中加入更高干扰。图7、图8和图9比较了输出变量的预测。
如图8、图9和图10所示,SVR方法的预测值与实际输出的测量值具有较大误差,该模型对随机误差或干扰的响应较差,当高干扰出现时预测会出现明显偏差,与实际值偏离较大,不能准确进行输出预测。Bi-SVR方法在高干扰情况下也会出现一些波动,但其预测值与实际值相差较小,只是稳定性有所下降。
表4为两种软测量方法在高干扰情况下的预测输出RMSE值。虽然在高干扰测试中Bi-SVR方法的RMSE值比低干扰大,但是对比所有的输出变量,它们仍然小于SVR方法的预测值。与SVR方法相比,Bi-SVR方法在丁醇浓度的平均预测RMSE低达0.025,远小于0.144。其它两个输出变量预测结果更差,而Bi-SVR方法在这两种情况下始终保持良好的预测结果。该测试很好地证实了Bi-SVR方法处理实际问题过程中,对不同程度干扰和测量非线性、时变性系统的超强能力和有效性。
4 结语
本文提出一种新的基于贝叶斯推断的多层支持向量机回归框架,用于丁醇发酵的多层软测量建模。该方法将贝叶斯推断与第一层SVR模型结合起来,以筛选出具有偏差的输入和输出值。第二层SVR模型建立在校准之后的数据样本之上,有效避免了干扰和偏差引起的模型不准确问题。而传统的SVR方法受此影响,其预测能力因测量偏差和误差而显著降低。
将所提出的Bi-SVR方法应用于丁醇发酵过程中,并将其性能与常规SVR方法的软测量预测能力进行比较,两次测试样本具有不同水平干扰。预测结果表明,Bi-SVR方法能够得到更准确的预测输出,优于传统SVR方法,具有更高的鲁棒性。以贝叶斯推断的自我协调能力与非线性处理能力,结合从支持向量机继承强大的泛化能力集成的Bi-SVR方法,有望成为微生物发酵过程的优选软测量建模方法。
参考文献:
[1] 高越,郭晓鹏,杨阳,等.生物丁醇发酵研究进展[J].生物技术通报,2018,34(8):27-34.
[2] 姜哲宇,刘元清,朱湘临,等.基于KFCM和AMDE-LSSVM的软测量建模方法[J].计算机测量与控制,2018,26(8):46-50,92.
[3] 高世伟,赵力.一种基于支持向量机的软测量建模方法[J].自动化仪表,2017,38(7):42-45.
[4] 张亚男.基于相关向量机的软测量建模技术及应用研究[D].无锡:江南大学,2017.
[5]潘宇雄,任章,李清东.动态贝叶斯最小二乘支持向量机[J].控制与决策,2014,29( 12):2297-2300.
[6]邱禹,刘乙奇,吴菁,等.基于深层神经网络的多输出自适应软测量建模[J].化工学报,2018.69( 7):3101-3113.
[7]LIU S T, GAOX W, QIWH, et al. Soft sensor modelling of propyleneconversion based ona Takagi-Sugeno fuzzy neural net,vork optimizedwith independent component analysis and mutual information [J].Transactions of the Institute of Measurement and Control, 2019. 41 (3):193-199.
[8]秦云月.基于支持向量机和神经网络模型的识别[J].电子技术与软件工程,2018(13):247-248.
[9] 杨凯,孙玉梅,王莉,等.基于ICA变量分组的集成软测量方法研究[J].北京理工大学学报,2018,38(6):631-636.
[10]ZHENG W,CHENG S,LI Z.Soft-sensing modeling and intelligentoptimal control strategy for distillation vield rate of atmospheric distil-lation oil refining process[ J]. Chinese Journal of Chemical Engineer-ing, 2018(6):964-968.
[11]汤文超.基于贝叶斯网络和支持向量机的尾矿库溃坝风险预警方法研究[D].武汉:武汉理工大学,2017.
[12] 陈若曦.基于贝叶斯证据框架优化的LS-SVM预测模型在空间电力负荷预测方法中的应用研究[D].天津:天津理工大学,2017.
[13]YU X K, LI J X, XU J.Nonlinear filtering in unknown measurementnoise and target tracking system by variational bayesian inference[J]. Aerospace Science and Technology, 2018(5):175-179.
[14]YU J.A nonlinear kernel gaussian mixture model based inferentialmonitoring approach for fault detection and diagnosis of chemical pro-cesses[Jl. Chemical Engineering Science, 2012, 68(1):506-519.
[15]夏莘媛,戴靜,潘用科,等.基于贝叶斯证据框架下SVM的油层识别模型研究[J].重庆邮电大学学报(自然科学版),2016, 28(2):260-264. 272.
[16] 方云录,苗茹.时间规整耦合线性判别分析的动作识别算法[J].计算机工程与设计,2018.39(11):3468-3474, 3499.
[17] 马科,符春晓,刘建,等.基于DTW的贝叶斯方法在睡眠和唤醒分类中的应用[J].计算机系统应用,2018,27(1):195-200.
[18]蔡的.连续发酵生产生物丁醇新工艺[D].北京:北京化工大学, 2013.
[19] 圣亚春.拜氏梭菌F-6合成丁醇发酵工艺优化及其动力学研究[D].哈尔滨:哈尔滨工业大学,2017.
[20]ZHOU Q, LIU Y, YUAN W Q.Kinetic modeling of lactic acid andacetic acid effects on butanol fermentation bv clostridium saccha-roperbutylacetonicum[ Jl. Fuel, 2018( 226): 1050-1057.
[21] MYUNC OH JANG, GYUNCHYUN CHOI. Techno-economic analy-sis of hutanol production from lignocellulosic biomass bv concentrat-ed acid pretreatment and hydrolysis plus continuous fermentation[J].Biochemical Engineering Journal, 2018( 134): 957-963.
(责任编辑:杜能钢)
作者简介:朱湘临(1963-),男,江苏大学电气信息工程学院教授、硕士生导师,研究方向为微生物发酵设备及其检测技术;顾雯炜(1995-),男,江苏大学电气信息工程学院硕士研究生,研究方向为工业过程检测与优化控制;王博(1982-),男,博士,江苏大学电气信息工程学院副教授、硕士生导师,研究方向为复杂工业过程的建模与优化控制。
