基于V2G技术的电动汽车实时调度策略
2020-06-18陈凯炎牛玉刚
陈凯炎,牛玉刚
基于V2G技术的电动汽车实时调度策略
陈凯炎,牛玉刚
(华东理工大学化工过程先进控制和优化技术教育部重点实验室,上海 200237)
随着电动汽车逐渐普及,其对电网的影响也不断扩大。为加强电动汽车与电网间协作,充分利用电动汽车在电网能量调度中的高度灵活性,提出一种基于V2G技术的电动汽车实时调度策略。首先以降低充电成本和网损成本为目标,建立电动汽车调度模型。然后通过构建网损灵敏度指标分析电网节点性能,基于电网负荷制定分时电价,通过潮流计算和凸优化算法实时求解得到电动汽车充放电策略。最后以IEEE 33节点配电网为例验证了所提策略可以有效降低充电成本与网损成本,同时分析了电动汽车渗透率、V2G占比对车网协作效果的影响。
电动汽车;V2G;网损;实时优化
0 引言
电动汽车(Electric Vehicle, EV)作为一种使用清洁能源、零排放的新型交通工具,在近年来得到广泛使用。随着电动汽车在电力系统中的渗透率逐步升高,其对电力系统的影响力也日益增大。自然状态下电动汽车的充放电行为具有较大的盲目性和随机性,难以实现个体与电网的协作。根据电动汽车相关统计,电动汽车入网时间分布与电网负荷变化规律大致吻合,即在峰值时刻充电需求大,非峰值时刻充电需求小。因此电动汽车无序充电极易加剧负荷峰谷差,使电网承担更大的压力。大量电动汽车的无协作充电则可能对电网整体稳定性产生不利影响,造成额外的经济损失[1-3]。
电动汽车具有其他负荷类型所不具备的灵活性和可调度性。此外,部分电动汽车具有电池电量回馈电网(Vehicle-to-Grid, V2G)的能力,即该类电动汽车既可视为负荷,也可视为储能电池[4-5]。若通过合理的调度策略充分利用V2G技术,对电动汽车充放电行为进行规划,加强车车、车网之间的协作,不仅可以进一步降低电动汽车充电成本和网损成本,还可以达到服务电网,改善电网负荷曲线的效果[6-7]。
为对电动汽车进行有序控制,文献[8]提出了一种集中式算法,使电动汽车在保证电网稳定的前提下最大化充电速率,结果表明有序充电下能量利用率和负荷曲线均有改善;文献[9]以充电站运营商购电成本最小为目标,提出了电动汽车分时充电价格的制定方法,实现智能电网中充电负荷的友好接入;文献[10]提出模糊化的电动汽车充电网络规划模型,采用遗传算法对电动汽车充电进行多目标优化。这些研究表明电动汽车有序充电可以同时兼顾多个目标,效果显著。但未考虑电动汽车能量回馈电网,仅将电动汽车视作一种高度灵活的负荷。
为加强电动汽车与电网的双向协作,文献[11]基于电力市场模型阐述了具有充放电能力的电动汽车对负荷调度、能源成本的影响;文献[12]在满足电网功率限制条件下提出了考虑用户因素的电动汽车充放电控制策略,使运营商和用户均获益;文献[13]通过对发电量和负载统计建模进行日前优化,使包含电动汽车负荷的日负荷曲线更好地跟踪发电曲线。这些研究强调利用V2G技术,但未在调度中充分考虑网损等与电网密切相关的评价指标,其调度策略缺乏实际性。
基于上述分析,本文提出了一种结合电网模型的电动汽车实时调度策略,对大规模电动汽车进行有序控制。充分考虑电动汽车与电网的协作能力,通过构建网损灵敏度指标分析节点性能,将电动汽车充放电行为与网损成本结合,基于潮流计算和凸优化算法进行实时规划,在保证按时完成充电任务的前提下充分利用电动汽车V2G功能降低充电成本和电网的网损成本,同时具有改善电网负荷波动、提升电网稳定性的效果。
1 电动汽车调度模型
电动汽车调度策略由调度中心制定并执行[14]。调度中心是一个负责实现区域内电动汽车与电网协作的信息中心,具有采集、发布信息和计算的能力。电动汽车入网后就需要接受调度中心的集中调度。如图1所示,在用户将电动汽车接入电网后,用户需要为其车辆设定离网时间和目标电量,并将这些信息与电动汽车的初始电量等数据上传到调度中心。在接入电网的时间内,电动汽车处于可调度状态,其充放电行为受调度中心控制。调度中心在保证按时完成所有车辆充电任务的前提下制定充放电调度策略,并在电动汽车达到离网时间时将其切出电网。
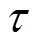
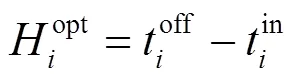
其中:为第i辆电动汽车的可调度时间;为入网时间;为用户设定的目标离网时间。
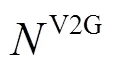
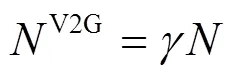

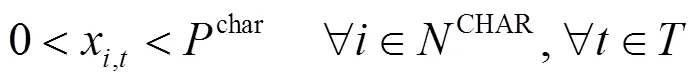
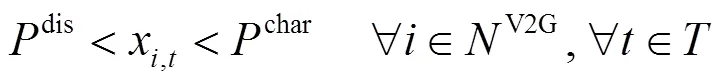
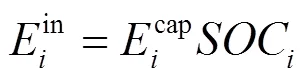
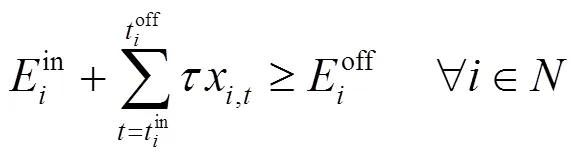
同时,电池电量在可调度时间内的任意时刻均满足:
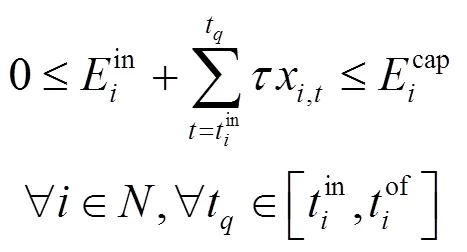
1.1 成本分析
1) 充电成本
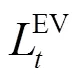
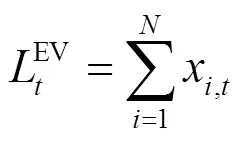
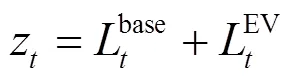
系统实时电价关于每个时间段内的总负荷线性变化,即:
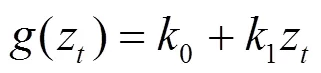
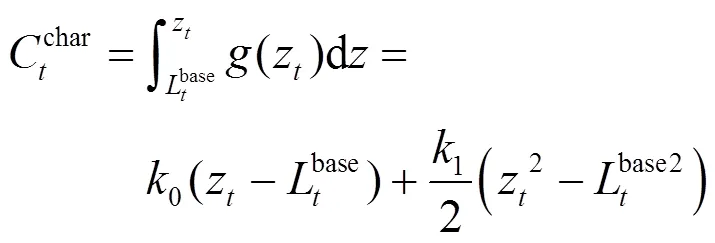
电动汽车充电总成本为
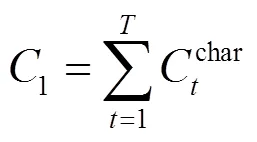
2) 网损成本
电动汽车接入电网节点后,以节点注入功率的形式对电网产生影响。在电网实际运行中,网损是造成的经济损失的一大来源。对含有条支路的电网进行潮流计算,支路的有功损耗为

时间段内的网损成本为
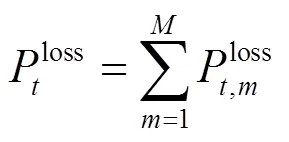
则网损总成本为
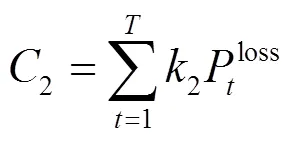
3) 总成本
一个调度循环周期内所有电动汽车完成充电任务的总成本为
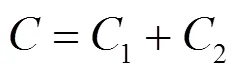
1.2 问题描述
本文目标为在保证完成电动汽车充放电任务的前提下,使总成本最小。则优化问题表述如下:
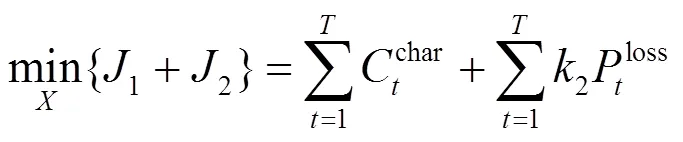
subject to:
(19)
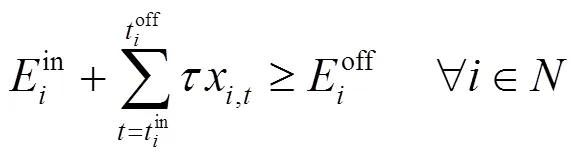
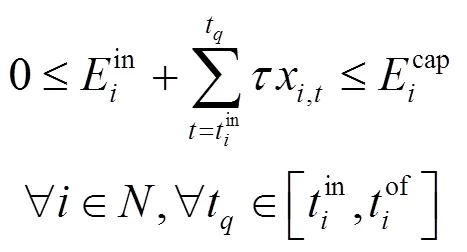
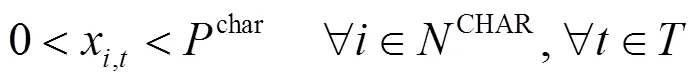
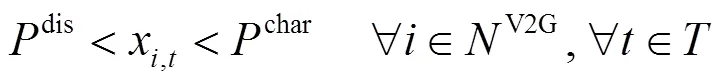
2 电动汽车实时调度策略
2.1 实时算法的优化范围
全局算法得到最优调度策略的前提是准确的电动汽车全天预测数据。而电动汽车入网时间、初始状态具有较大的随机性,不宜使用全局算法[15]。本文采用的实时调度策略不需要电动汽车全天预测信息,而是对每个时间段内处于可调度状态的电动汽车进行实时优化,得到针对当前时间段的最优调度方案。
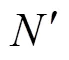
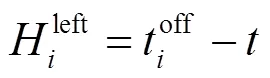
如图2所示,为使实时算法的充放电规划能充分配合一定时长内的基础负荷变化情况,其优化范围动态变化。优化范围的大小取当前时间段可调度车辆的剩余可调度时间的最大值:
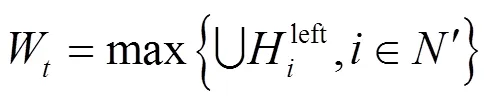
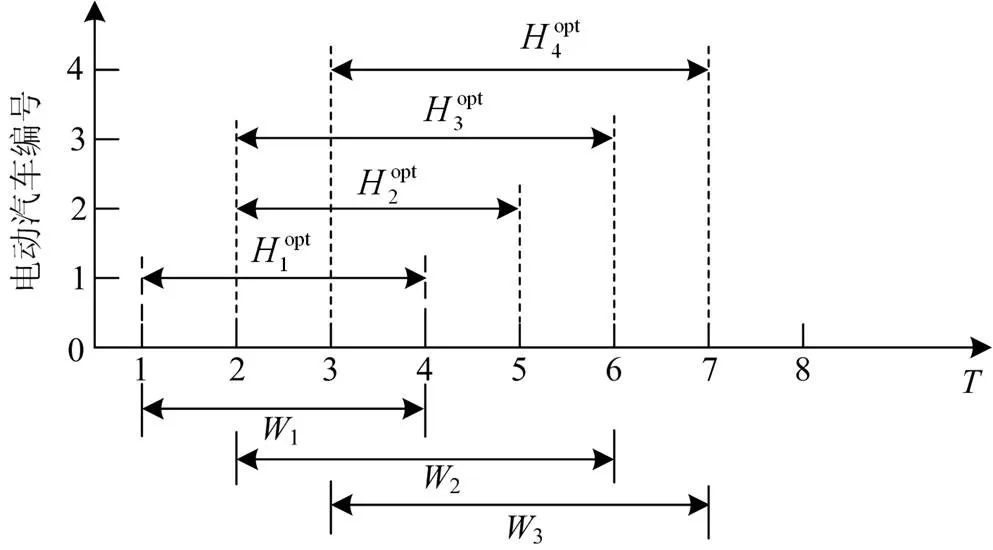
图2 各时间段的优化范围
如图3所示,每个时间段计算得到的调度策略长度均为相应的优化时间窗,如Solution 1长度为3。电动汽车将收到的调度策略的首部作为当前时间段的充放电策略,如时间段2所选用的策略为S2-1。全天的调度策略即由这些部分组成。

图3 各时间段的调度策略
2.2 网损灵敏度指标
电动汽车充放电行为引起的网损成本与节点性能紧密相关。同时,在优化迭代过程中调度策略会为各节点分配不同的负荷量,直接通过潮流计算的方式计算网损会大大增加优化过程的耗时,导致调度中心不能及时向所有电动汽车用户提供充放电规划。因此考虑使用网损灵敏度(Power Loss Sensitivity, PLS)作为决策的辅助手段。
网损灵敏度表示网损对节点注入功率的灵敏度,宏观上可以视为电网节点增加单位负荷量后引起的网损大小。计算网损灵敏度时,首先将当前时间段的基础负荷分配到电网中,再依次计算网损关于节点有功功率的偏微分,表达式为
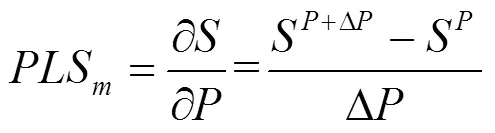
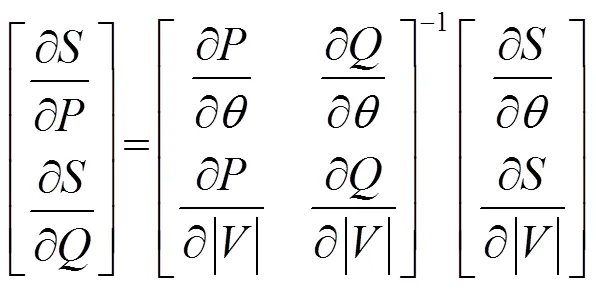
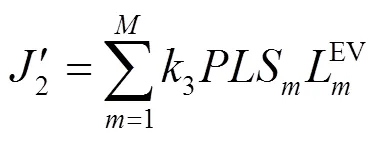
此外,网损灵敏度基于电网基础负荷计算得到,即每个时间段对应一组网损灵敏度。由于调度策略采用的基础负荷为日前预测数据,因此可以在每日调度开始前将所有时间段的网损灵敏度离线计算完毕。在后续优化过程中只需要依据电动汽车在相应节点的充放电行为即可计算网损灵敏度指标,从而避免了反复进行潮流计算。
2.3 算法描述
根据上述分析,将1.3节的优化问题修改如下。
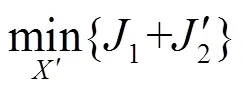
subject to:
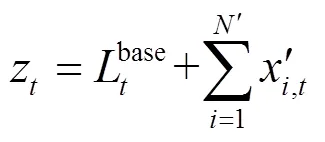
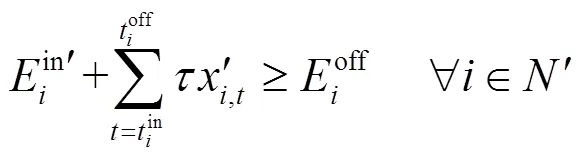
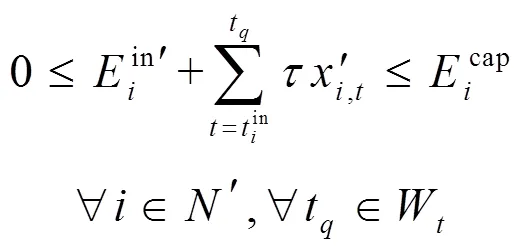
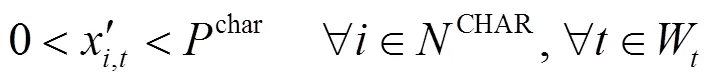
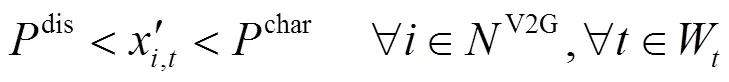
由于目标函数为凸函数,并且所有约束条件均为线性约束,因此该优化问题可以采用凸优化方法解决。本文采用内点法进行求解。在得到充放电控制矩阵后取首列作为当前时间段的调度策略执行。将基础负荷与电动汽车负荷更新到电网中进行潮流计算,计算当前时间段的网损成本和充电成本。在一个调度循环周期结束后计算总成本。
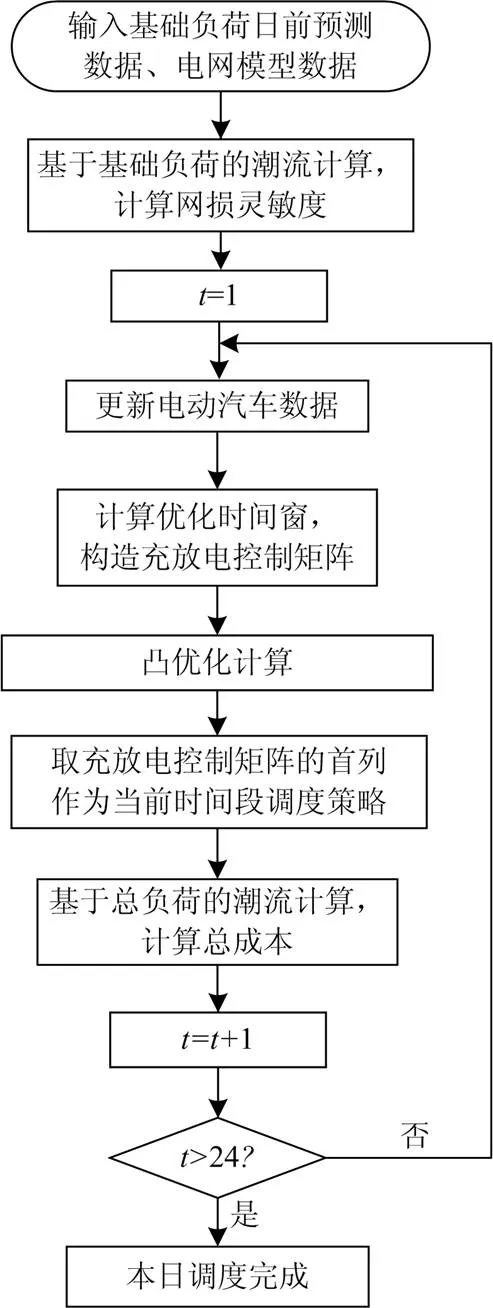
图4 实时优化流程图
3 仿真实例
3.1 仿真环境
仿真环境基于IEEE 33节点配电网测试系统建立[16]。该测试系统结构如图5,电压基准值12.66 kV,平衡节点为节点1。
负荷数据来自文献[17]中的2011年美国交通部对全美家用车辆行驶的调查结果(National Household Travel Survey, NHTS),包括电动汽车用户的行驶特性、入网时间、初始荷电状态等关键参数。
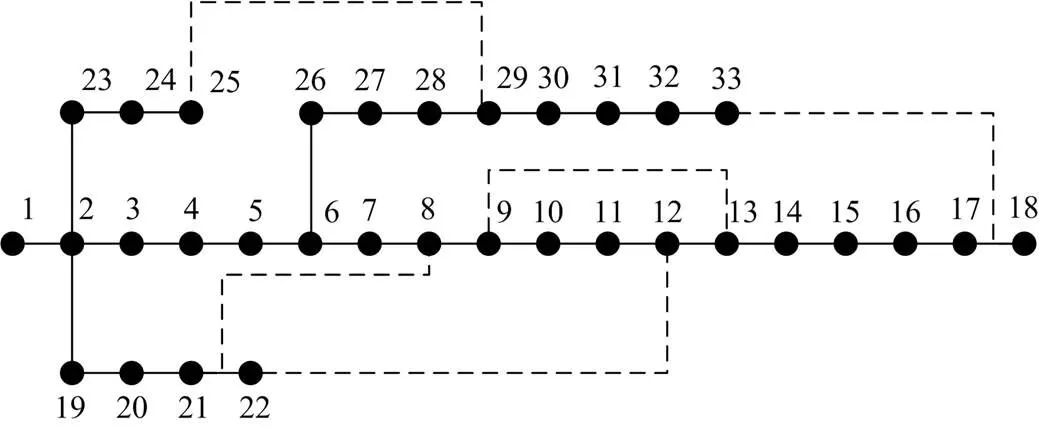
图5 IEEE 33节点配电网测试系统
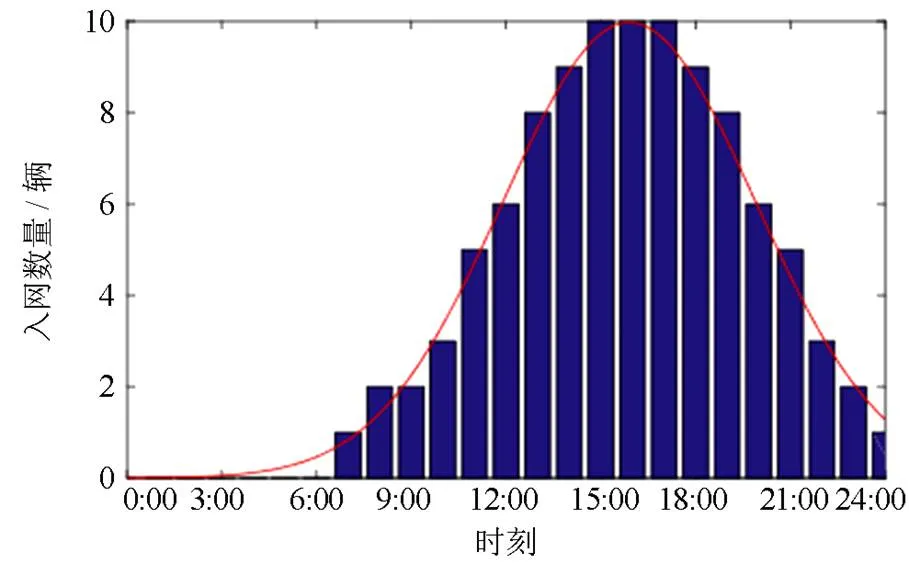
图6 各时间段入网电动汽车数量
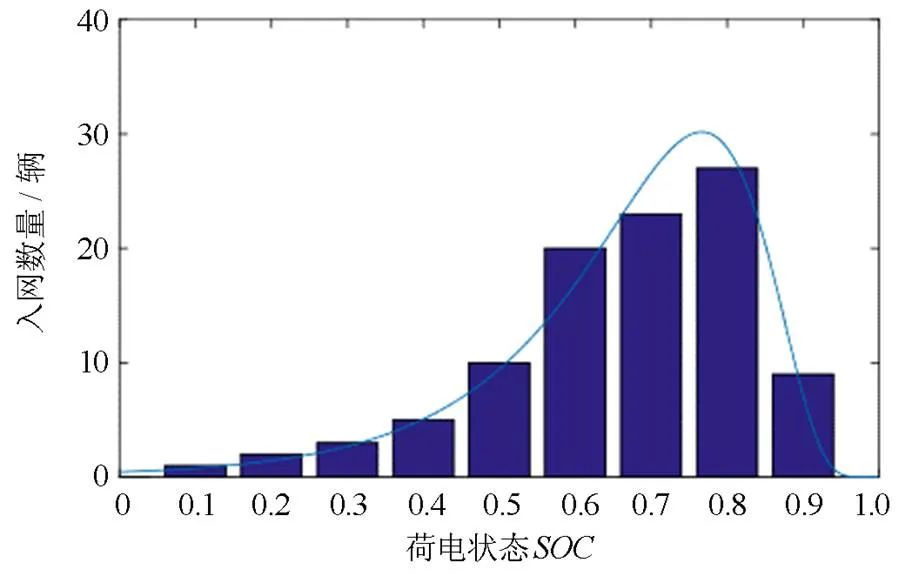
图7 电动汽车初始荷电状态
其他仿真相关参数设置如表1。其中,电动汽车电池最大容量15 kWh,用户的目标离网电量为满电,充电、放电速率上限均为3 kW。
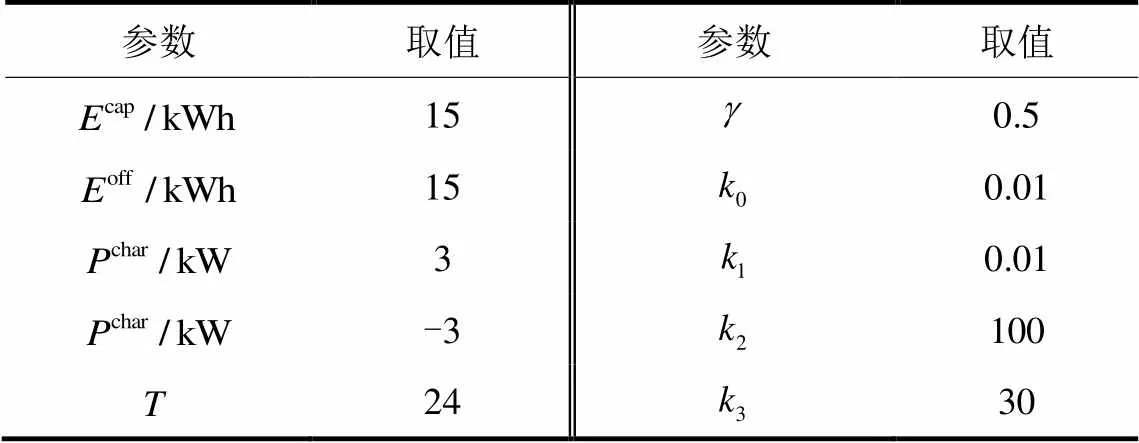
表1 仿真相关参数设置
考虑到调度策略的连续性,要求每日6:00前完成当前周期内所有车辆充电任务,同时更新日基础负荷预测数据。因此,本文仿真的初始时刻为6:00,至次日6:00结束。
在原始状态下,电动汽车从接入电网开始以允许的最大充电速率充电,电池充电完毕后切出电网。由此得到原始动态下总负荷与基础负荷对比情况如图8所示。电动汽车大量接入的时刻与基础负荷的峰值时刻相近,导致大量电动汽车在电网负担较大时进行充电,充电成本和网损成本大大增加。而在3:00附近为电网非峰值时刻,电网负担较小,电价较低,仅有少量电动汽车进行充电。
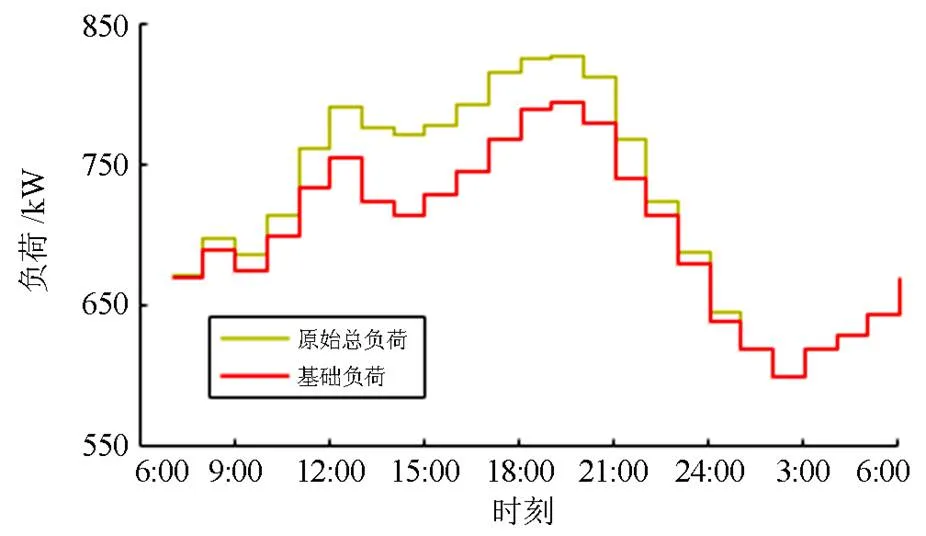
图8 原始状态总负荷与基础负荷对比
基于基础负荷计算各时间段的网损灵敏度。图9为=1时的各电网节点网损灵敏度。
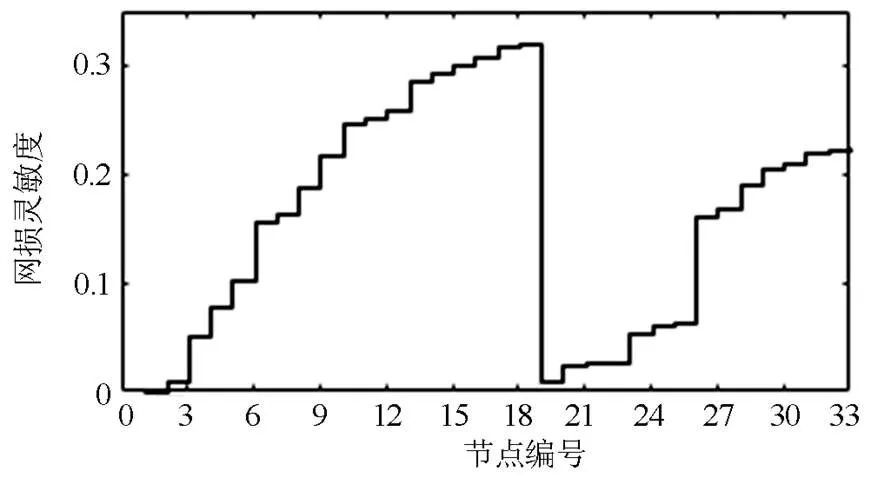
图9 t=1时各电网节点网损灵敏度
显然节点18、节点33等节点具有较大的网损灵敏度,在网损灵敏度指标计算中会产生较大的影响。其中节点1为电网模型中的平衡节点,网损灵敏度为0,且该节点禁止接入电动汽车。
3.2 仿真结果分析
3.2.1充放电行为分析
根据图10、图11的负荷统计,调度中心针对出现在12:00附近、20:00附近的基础负荷峰值均进行了规避,避免高电价充电。由于峰值大小间接决定了调度中心的调度能力,因此在峰谷差距较小的12:00附近,电动汽车净负荷变化并不明显。导致这一现象的另一原因是此时接入电网并可供调度的电动汽车数量有限,无法实现接大规模的负荷转移。由图12可以看到,在12:00附近,V2G车辆放电供应其他车辆充电,使得电动汽车净负荷接近于零。
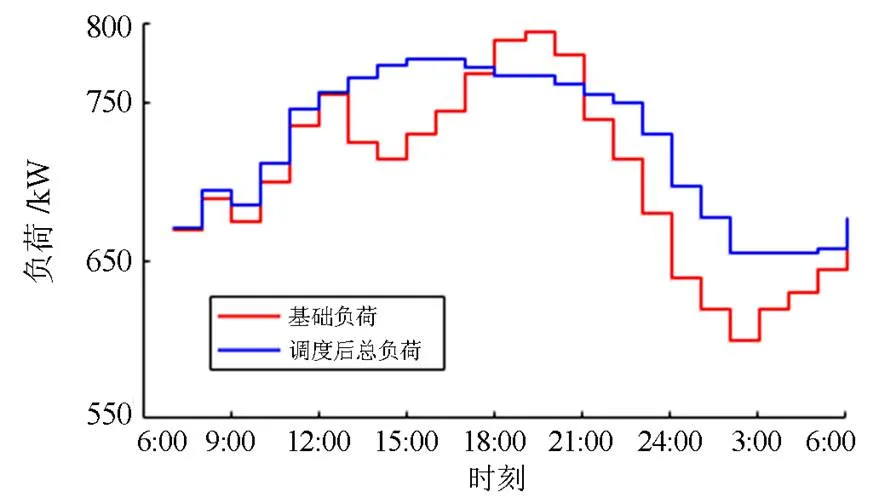
图10 调度后总负荷与基础负荷对比
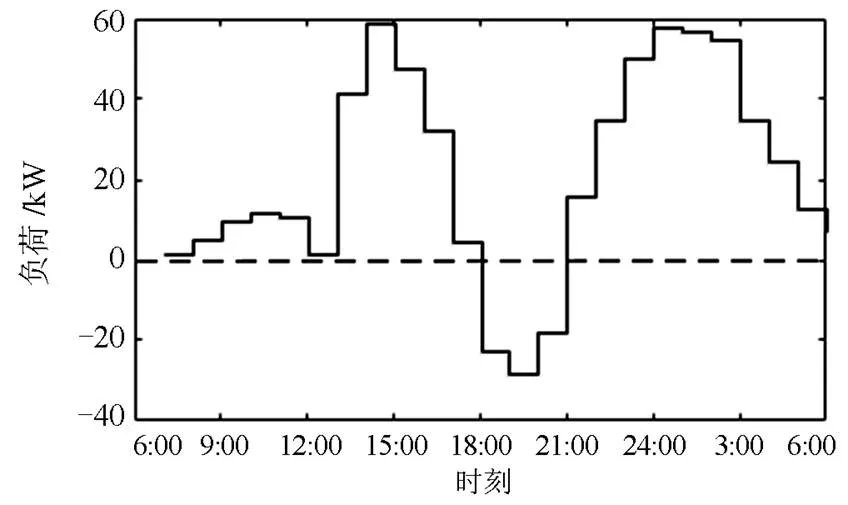
图11 调度后电动汽车净负荷
在峰谷差距较大的20:00附近,电动汽车净负荷为负,电动汽车的充放电行为具体表现为大量V2G车辆向电网馈电,少部分仅支持充电的电动汽车进行充电。由图12可以看到20:00附近由于大量电动汽车进行放电,调度后总负荷明显低于基础负荷曲线,负荷峰值时期的充电成本与网损成本得到大幅降低。
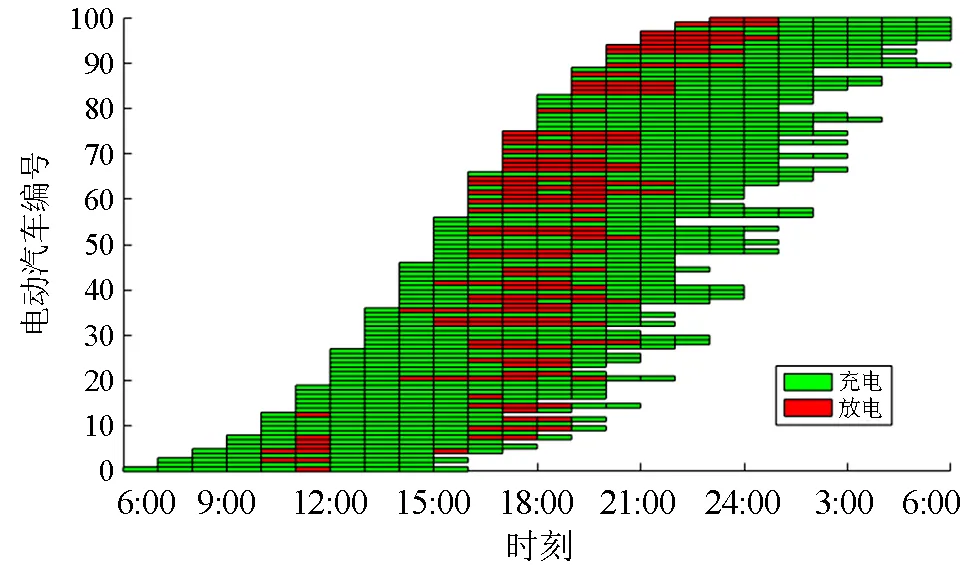
图12 电动汽车充放电行为记录
此外,在3:00、15:00等非峰值时刻,电网整体负担较轻,电动汽车的充放电行为具体表现为集体充电,抬高了非峰值时刻总负荷。
对具体数据分析发现,原始状态下电网总负荷峰值为19:00的826.5 kW,次峰值为12:00的791.0 kW,总负荷最低值为4:00的601.8 kW,峰谷差为224.7 kW,标准差为73.7。应用调度策略后总负荷峰值为14:00的777.9 kW,并且在11:00至21:00内总负荷均保持在745.3~777.9 kW。总负荷最低值为5:00的654.7 kW,峰谷差为123.2 kW,标准差为46.5。
从宏观上来看,实时算法实现了在较大时间范围内的负荷转移,达到了削峰填谷的效果。这也是所提策略能够降低各项成本的主要原因。
3.2.2充电成本与网损成本分析
2.2节的分析表明,充电成本与网损成本均与总负荷曲线紧密相关。
对调度前后的案例进行成本分析。原始状态下充电成本为1 931.4元,网损成本177.5元,平均每车每日总成本为21.1元;调度后充电成本为1 743.5元,网损成本为163.4元,平均每车每日总成本为19.1元。
调度后充电成本降低9.7%,网损成本降低7.9%,平均每车每日总成本降低9.5%。
图12同时也表明大部分电动汽车的充放电行为较为规律,表现为峰值时期放电,低谷时期充电。仅有极少量电动汽车在入网时间内进行了反复多次的充放电,因此本调度策略也在一定程度上降低了电池损耗的成本。
3.3 V2G比例对车网协作的影响
如图13所示,随着V2G比例的升高,总负荷曲线逐渐趋于平缓。在抑制负荷波动的效果上,三个案例均取得良好的效果,这主要是因为算法对充电行为也进行了充分规划,起到了负荷转移的作用,而放电行为的规划令负荷曲线进一步趋于平滑。三个案例中,50%比例相对于25%比例提升较为明显,在峰值时期负荷有较为明显的降落,在非峰值时刻负荷有较为明显的抬升,峰谷差缩小。而75%比例相对于50%比例有一定的改善,但提升较小。本算法对V2G比例的要求并不严苛,在V2G比例为50%左右时,即可取得比较理想的结果。
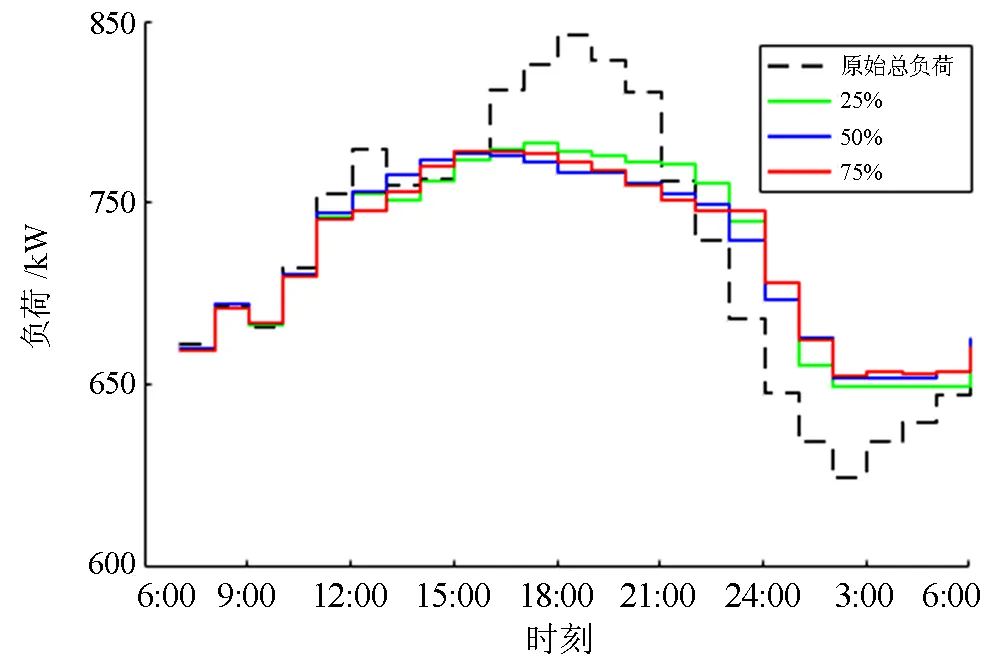
图13 不同V2G比例下的负荷调度情况
表2表明,在本文的电价制度下,对于电动汽车用户来说,电动汽车放电是一种降低总成本的有效手段。当电网中的电动汽车V2G比例较低时,出现负荷紧张时对放电行为的需求度较高,电动汽车放电效果明显,成本大幅降低;但是当V2G比例较高时,电量需求被大幅稀释,因此成本无法进一步降低。
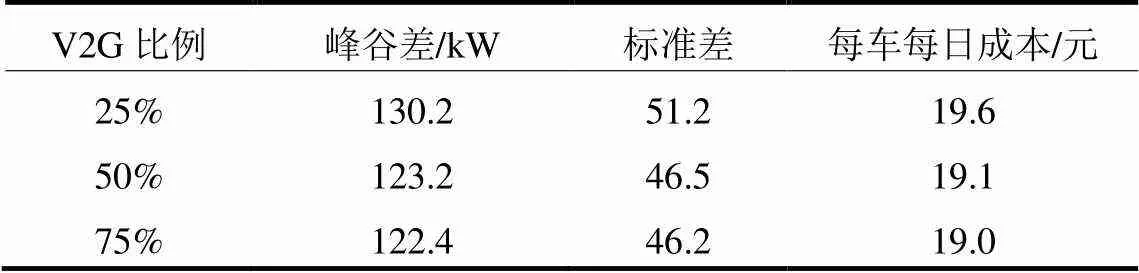
表2 不同V2G比例下的调度效果
3.4 渗透率对车网协作的影响
统计数据表明电动汽车正处于高速发展中,电动汽车在电网中的渗透率也随之升高。考量不同渗透率下电动汽车对电网的影响非常重要[18-20]。不同渗透率的电动汽车在本算法调度下表现如图14。
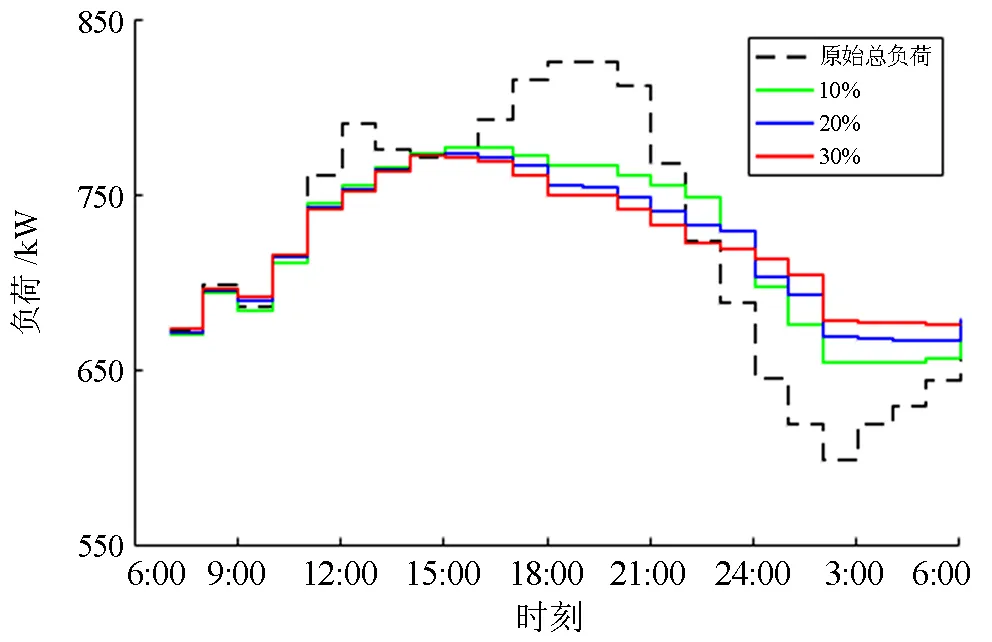
图14 不同渗透率下的负荷调度情况
电动汽车渗透率分别为10%、20%、30%时的负荷曲线表明随着渗透率增加,电动汽车削峰填谷的能力得到增强,负荷曲线更加平坦,意味着在本文电价制度下总成本进一步降低。调度效果如表3所示。
值得注意的是,在12:00的次峰值附近,三种渗透率的负荷曲线区别不大。一是由于此时可调度车辆较少;二是由于此时负荷波动幅度较小,在渗透率较小的情况下电动汽车也能起到良好的调节效果。在20:00的峰值附近和3:00的低谷值附近,30%渗透率的电动汽车表现明显优于其余两者,表明较高的渗透率保证了电动汽车有充足的负荷吞吐量,用于应对大规模的负荷波动[21-22],防止出现某一时间段的充电成本与网损成本过高的情况。
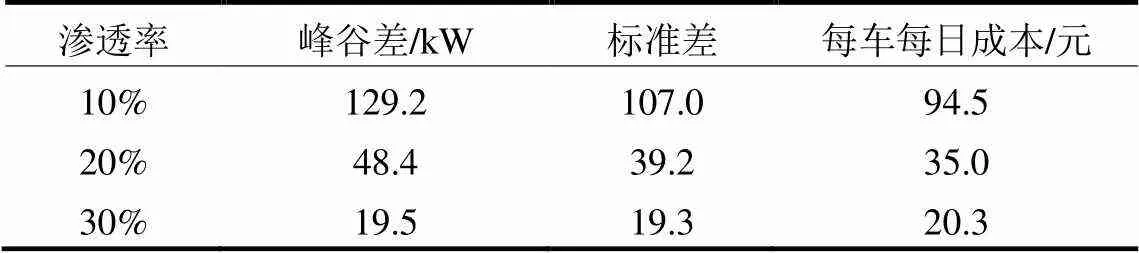
表3 不同渗透率下的调度效果
以上实验表明,采用所提的调度策略对电动汽车充放电行为进行规划时,所有电动汽车均能按时按量完成用户设定的充电任务。在此基础上,调度策略有效降低了充电成本与网损成本,同时还具有改善电网负荷曲线的效果。
调度策略对V2G比例的要求并不苛刻。V2G比例为25%时依然可以取得较好的效果。随着V2G比例的提升,调度效果有所改善。
调度策略的效果对电动汽车渗透率比较敏感。在高渗透率的案例中,总成本与负荷曲线的改善效果更明显。从调度循环周期来看,在初始时段电网中的可调度车辆总数较少,对电能的吞吐量不足,调度中心对电网负荷的调节能力相对薄弱;在中间时段随着大量电动汽车入网,调度中心对负荷峰值的响应能力大大提升,能更好地实现降低成本的调度目标。
4 结论
本文提出了一种基于V2G技术的电动汽车实时调度策略,根据网损灵敏度值表分析节点性能,利用潮流计算与凸优化算法得到充放电策略。仿真表明本文方法能够有效降低电动汽车充电成本与电网的网损成本。主要结论如下:
1) 在分时电价制度下,采用凸优化算法实时求解得到的充放电策略可以在按时完成充电任务的前提下有效降低充电成本与网损成本。
2) 策略制定时通过构建网损灵敏度指标充分考虑了节点性能对成本的影响,同时简化了网损成本计算过程。
3) 所提策略在不同的电动汽车渗透率和V2G占比下均有降低成本、优化负荷曲线的效果。
[1] HAFIZ F, DE QUIEROZ A R, HUSAIN I, et al. Charge scheduling of a plug-in electric vehicle considering load demand uncertainty based on multi-stage stochastic optimization[C] // North American Power Symposium, September 17-19, 2017, Morgantown, WV, USA: 1-6.
[2] WEN C K, CHEN J C, TENG J H, et al. Decentralized plug-in electric vehicle charging selection algorithm in power systems[J]. IEEE Transactions on Smart Grid, 2012, 3(4): 1779-1789.
[3] 王彪, 尹霞. 实时电价下含V2G功能的电动汽车理性充放电模型及其分析[J]. 电力系统保护与控制, 2016, 44(24): 90-96.
WANG Biao, YIN Xia. Modeling and analysis on the rational charging and discharging of electric vehicle with V2G function under real-time prices[J]. Power System Protection and Control, 2016, 44(24): 90-96.
[4] 张祥文, 江星星, 王龙. 配电网接纳电动汽车能力评估方法研究[J]. 电力系统保护与控制, 2015, 43(12): 14-20.
ZHANG Xiangwen, JIANG Xingxing, WANG Long. Research on assessment methods of distribution network’s ability of admitting electric vehicles[J]. Power System Protection and Control, 2015, 43(12): 14-20.
[5] 马益平. 考虑电动汽车调度的微电网混合储能容量优化配置[J]. 电力系统保护与控制, 2017, 45(23): 98-107.
MA Yiping. Hybrid energy storage capacity optimization configuration for micro-grid considering EV scheduling[J]. Power System Protection and Control, 2017, 45(23): 98-107.
[6] 肖浩, 裴玮, 孔力. 含大规模电动汽车接入的主动配电网多目标优化调度方法[J]. 电工技术学报, 2017, 32(增刊2): 179-189.
XIAO Hao, PEI Wei, KONG Li. Multi-objective optimization scheduling method for active distribution network with large scale electric vehicles[J]. Transactions of China Electrotechnical Society, 2017, 32(S2): 179-189.
[7] 舒隽, 唐刚, 韩冰. 电动汽车充电站最优规划的两阶段方法[J]. 电工技术学报, 2017, 32(3): 10-17.
SHU Jun, TANG Gang, HAN Bing. Two stage method for optimal planning of electric vehicle charging station[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 10-17.
[8] RICHARDSON P, FLYNN D, KEANE A. Local versus centralized charging strategies for electric vehicles in low voltage distribution systems[J]. IEEE Transactions on Smart Grid, 2012, 3(2): 1020-1028.
[9] 常方宇, 黄梅, 张维戈. 分时充电价格下电动汽车有序充电引导策略[J]. 电网技术, 2016, 40(9): 2609-2615.
CHANG Fangyu, HUANG Mei, ZHANG Weige. Research on coordinated charging of electric vehicles based on TOU charging price[J]. Power System Technology, 2016, 40(9): 2609-2615.
[10] 丁丹军, 戴康, 张新松, 等. 基于模糊多目标优化的电动汽车充电网络规划[J]. 电力系统保护与控制, 2018, 46(3): 43-50.
DING Danjun, DAI Kang, ZHANG Xinsong, et al. Network planning for electric vehicle charging based on fuzzy multi-objective optimization[J]. Power System Protection and Control, 2018, 46(3): 43-50.
[11] VAGROPOULOS S I, BALASKAS G A, BAKIRTZIS A G. An investigation of plug-in electric vehicle charging impact on power systems scheduling and energy costs[J]. IEEE Transactions on Power Systems, 2017, 32(3): 1902-1912.
[12] 王鑫, 周步祥, 唐浩. 考虑用户因素的电动汽车有序充放电控制策略[J]. 电力系统保护与控制, 2018, 46(4): 64-69.
WANG Xin, ZHOU Buxiang, TANG Hao. A coordinated charging/discharging strategy for electric vehicles considering customers’ factors[J]. Power System Protection and Control, 2018, 46(4): 64-69.
[13] 刘东奇, 王耀南, 袁小芳. 电动汽车充放电与风力/火力发电系统的协同优化运行[J]. 电工技术学报, 2017, 32(3): 18-26.
LIU Dongqi, WANG Yaonan, YUAN Xiaofang. Cooperative dispatch of large-scale electric vehicles with wind-thermal power generating system[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 18-26.
[14] XIA M, LAI Q, ZHONG Y, et al. Aggregator-based interactive charging management system for electric vehicle charging[J]. Energies, 2016, 9(3): 1-14.
[15] SACHAN S, ADNAN N. Stochastic charging of electric vehicles in smart power distribution grids[J]. Sustainable Cities and Society, 2018, 40: 91-100.
[16] BARAN M E, WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.
[17] GARCíA-VILLALOBOS J, ZAMORA I, EGUIA P, et al. Modelling social patterns of plug-in electric vehicles drivers for dynamic simulations[C] // 2014 IEEE International Electric Vehicle Conference, December 17-19, 2014, Florence, Italy: 1-7.
[18] 刘琰, 何伟哲. 电动汽车充电模式选择与充电负荷计算的研究[J]. 电网与清洁能源, 2017, 33(10): 129-133.
LIU Yan, HE Weizhe. Research on charging mode selection and charging load calculation of electric vehicles[J]. Power System and Clean Energy, 2017, 33(10): 129-133.
[19] 周天沛, 孙伟. 基于微网的电动汽车与电网互动技术[J]. 电力系统自动化, 2018, 42(3): 98-104.
ZHOU Tianpei, SUN Wei. Electric vehicle-to-grid technology based on microgrid[J]. Automation of Electric Power Systems, 2018, 42(3): 98-104.
[20] MOON S K, KIM J O. Balanced charging strategies for electric vehicles on power systems[J]. Applied Energy, 2017, 189: 44-54.
[21] 娄素华, 张立静, 吴耀武, 等. 低碳经济下电动汽车集群与电力系统间的协调优化运行[J]. 电工技术学报, 2017, 32(5): 176-183.
LOU Suhua, ZHANG Lijing, WU Yaowu, et al. Coordination operation of electric vehicles and power system under low-carbon economy[J]. Transactions of China Electrotechnical Society, 2017, 32(5): 176-183.
[22] 周强. 电动汽车充电服务互联互通问题的探讨[J]. 供用电, 2017, 34(1): 19-23.
ZHOU Qiang. Discussion on the interconnection of electric vehicle charging service[J]. Distribution & Utilization, 2017, 34(1): 19-23.
Real-time scheduling strategy of electric vehicle based on vehicle-to-grid application
CHEN Kaiyan, NIU Yugang
(Key Lab of Advanced Control and Optimization for Chemical Process, Ministry of Education, East China University of Science & Technology, Shanghai 200237, China)
As electric vehicles become more popular, their impact on the power grid is also increasing.In order to enhance the cooperation between electric vehicles and power grids and make full use of the high flexibility of electric vehicles in grid energy dispatching, this paper proposes a real-time dispatching strategy for electric vehicles based on V2G technology.To reduce the cost of charging and power loss, an electric vehicle scheduling model is established.Then, the grid node performance is analyzed by constructing the network loss sensitivity index, and the time-of-use electricity price is determined based on the grid load.Finally, the power flow calculation and convex optimization algorithm are used to solve the electric vehicle charging and discharging optimal strategy in real time. The proposed strategy is verified by IEEE 33-node distribution system, and the influence of electric vehicle penetration and V2G ratio on the cooperation between electric vehicle and grid is analyzed.
This work is supported by National Natural Science Foundation of China (No. 61673174).
electric vehicle; vehicle to grid; power loss; real-time optimization
转载自《电力系统保护与控制》2019年47卷14期
陈凯炎, 牛玉刚. 基于V2G技术的电动汽车实时调度策略[J]. 电力系统保护与控制, 2019, 47(14): 1-9.
CHEN Kaiyan, NIU Yugang. Real-time scheduling strategy of electric vehicle based on vehicle-to-grid application[J]. Power System Protection and Control, 2019, 47(14): 1-9.
10.19783/j.cnki.pspc.181011
国家自然科学基金项目资助(61673174)
2018-08-08;
2019-01-18
陈凯炎(1994—),男,硕士研究生,研究方向为电网与电动汽车负荷调度;E-mail: 2461365998@qq.com
牛玉刚(1964—),男,教授,博士生导师,研究方向为随机系统、无线传感网络、智能电网。
