品味问题内涵 凸显数学本质*——一以一道填空压轴题的教学为例

陈 静

(江苏省扬州大学附属中学,225002)

波利亚指出:“掌握数学就意味着善于解题.”对试题的探索,不仅能追本溯源,启发学生的多角度思考,最大限度地挖掘学生的思维潜能,还能更好地开发试题的教学功能[1].错误也是一种有价值的课程资源,近期有一道联考试题,作为填空题的压轴题,难度较大,得分率很低,笔者对这道近乎废题的难题进行再利用,把它作为课堂教学的探究资源,引导学生挖掘其隐含的思维价值,透视其蕴含的数学本质.

一、剖析考场得失 把脉解题思路

二、追溯题根本源 引导突破难点

师:在大家的考后反思中,我发现同学们对这道题的考场反应很丰富,这些都是珍贵的资源,让我们一起来开发吧.

师:初中学过“将军饮马”问题,其本质原理是两点之间的所有连线中,以线段长为最短(三角形两边之和大于第三边),这是一个公理,本题的最值问题能否转化为这一原理来解决?

师:这个式子可以转化为动点C到两定点距离之和?

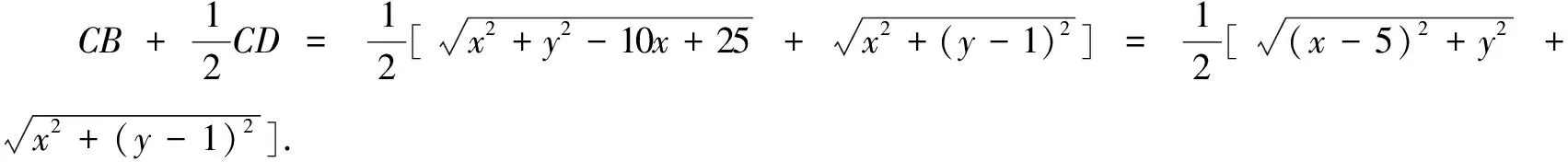
师:非常好!通过一系列的代数变形,将问题转换到“将军饮马”问题.这启示我们在解题时要注意转化、化归,由已知到未知,化复杂为简单,将生疏的问题转化为熟知的课本知识.解题时要注意优化计算,确保目标达成.

设计意图数学题能否简洁而富有创造性地解答,往往取决于是否能透过问题表象洞悉其蕴涵的数学本质.所谓数学本质,是指能真正反映数学学科本质规律的概念、原理、公理、定义、公式等等[2].对数学本质的领悟,是提升学生数学核心素养,促进学生数学知识的掌握、数学能力的形成的一个前提和必要条件.揭示数学本质,可将复杂问题简单化、深邃问题大众化,使学生容易理解和掌握.

三、多种视角探究 彰显数学魅力

(学生们陷入了思考)

师:这个想法不错,有探究的味道!没有点E坐标,如何继续?

师:逆向思维，这个做法很精彩!谁能接着生4的思路继续作答?

生5:该方程应该和x2+y2-2x-3=0是同一个方程,利用对应项系数相等,可以求出点E坐标，以下同解法1.

师:理解得非常透彻!请同学们按照这个解题思路,在演算纸上求出点E坐标.

(展示学生演算结果,得点E(5,0))

师:此解法的精彩之处在于意识到两次求得的点C的轨迹是同一个圆,用待定系数法确定点E坐标,优化解题思路,简化计算过程.

设计意图教会学生怎样思考,如何才能想到解题方法是解题教学的首要任务.教师要稚化自己的思想,诱导学生进行渐行渐深的探究,逐步暴露解题的思维过程.教师应搭建脚手架,引导学生将符号化的知识打开,将静态的知识激活,将碎片化的知识联结,获得自己对题目本质的理解与感悟,从而构建出自己的解题思路.

师:这个想法很有思考性,能解释一下阿氏圆吗?

(学生们陷入了思考)

师:(继续引导启发)这种成比例的问题,能否利用初中相似三角形的思路来解决呢?

师:好神奇!图形的力量太强大了!思考问题时,借助图形,充分运用平面几何知识,回归题目本质,可以降低运算量,使得解题更快捷.

设计意图加德纳说过:“数学的真谛就在于不断寻求用越来越简单的方法证明定理和解决数学问题.”充分运用初中所学的图形知识,构造相似三角形确定E点位置,求出点E坐标.该解法甚为巧妙,跳出了“数”的囹圄,从“形”的角度重新认识它,使形象思维与抽象思维相结合,能激发学生产生再创造性想象,还原了题目本质.

四、变式拓展延伸 提升思维品质

设计意图解题教学中做适当的拓展延伸,依据原问题本质进行一些有价值的变式探究,能够挖掘题目自身所蕴含的内在规律和本质,拓宽例题的教学功能,促进知识方法的迁移提升.精心设置问题的变式,可以激活学生的思维,多角度训练学生的思维,提高学生思维的深度和广度.

五、教学反思

1、立足学生认知基础,从学生熟知情境还原题根本质

从学生实际出发,遵循“最近发展区”原理,充分利用学生已有的知识储备,引导学生领悟题根本质,高屋建瓴地理解、掌握数学.这样的解题教学才能更好地启发学生弄清楚解法的来龙去脉,帮助学生提炼数学思想方法,确实提升学生数学解题能力.数学教学应该着眼于研究如何凸显数学的本质,如何精中求简、返璞归真，让学生享受数学本质探究的乐趣,领会和体验数学的价值和魅力.

2、逐步突破学生疑难点,在学生愤悱之时引出新方法

告知学生,他们会忘记;板演给学生看,他们会记住;让学生参与,他们就能在参与中彻悟.在解题教学中,学生困惑最多的就是为什么会想到这样的解题方法,而仅凭学生个人则无法想到问题的解题思路.对此,教师要善于在学生思维障碍处进行引导,做到“不愤不启,不悱不发”,这样才能帮助学生解除解题中的困惑,使解题思路逐步清晰明朗,解题过程自然流畅.因此,要解决深入研究问题的困难,就要针对解题的障碍之处进行适当调节,找到突破问题的关键节点,帮助学生走出思维的困境[3].在解题过程中,要充分暴露学生的思维活动,捕捉学生思维的闪光点,引领学生主动学习,促进学生积极思考,激发学生学习兴趣,指导学生学会数学学习的方法,从而全面提高学生的数学素养.

米山国藏说过:在学校学的数学知识,毕业后若没有什么机会用,一两年后很快就忘掉了.然而,不管他们从事什么工作,唯有深深铭刻在心中的数学精神、数学的思想方法、研究方法、推理方法和看问题的着眼点等,却随时随地发生作用,使他们终身受益.