时域取样定理在工程应用中的关键问题推导∗

方 敬 卢文锋 乔建苹 王春兴

(1.山东师范大学物理与电子科学学院，山东 济南 250014；2.山东建筑大学管理工程学院，山东 济南 250101)

0 引 言

奈奎斯特时域取样定理是信号与系统、数字信号处理和通信原理等电子信息类专业课程中均涉及到的重要定理[1-7].取样定理首先由美国电信工程师Nyquist于1928年提出[8]，后来香农对取样定理进行了证明[9].因为离散时间信号与连续时间信号相比具有易于存储、稳定性好和处理灵活等优点.因此，在实际应用中需要把连续信号转换成离散信号进行传输与处理.取样定理论述了当满足一定条件时，一个连续时间信号完全可以用该信号在等时间间隔上的采样值来表示.这些采样值包含了该连续信号的全部信息，由这些样本值可以恢复原始连续时间信号[10].可以说，取样定理在连续信号与离散信号之间架起了一座桥梁[2].然而，在目前出版的很多教材中，关于取样定理的论述仍然存在一些问题:如传统教材中为了推导取样信号与原始连续信号的频谱关系，将取样问题简化为理想取样，而这往往不符合实际，因为取样脉冲信号不等同于梳状函数；传统教材中通常只推导了原始连续信号与取样信号的频谱关系，而没有推导原始连续信号与离散信号的频谱关系，这是不严谨的；传统教材中很少考虑取样定理在实际应用中的混叠问题.本文针对这些问题对取样定理作进一步的推导和说明，力求解答学生学习过程中的疑惑，并为工程技术人员提供理论指导.

1 矩形脉冲取样

实际应用中，连续时间信号的取样由A/D转换器实现，连续时间信号x(t)通过一个电子开关，电子开关每隔时间(T)闭合一次，闭合持续的时间为τ，如图1(a)所示.取样信号xs(t)等于连续时间信号xa(t)与开关函数s(t)相乘，如图1(b)所示[11].

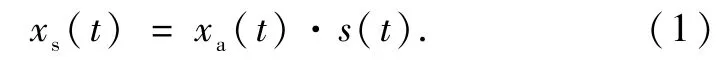
开关函数s(t)每隔T闭合一次，可以用周期性的矩形脉冲信号表示，如图2(a)所示.传统教材中为了简化问题，采用理想取样模型，即开关函数s(t)用梳状函数来代替，如图2(b)所示.然而，实际采样中，电子开关每次闭合持续的时间τ不等于零，而且脉冲的幅度是1，而梳状函数的幅度趋于无穷.因此，基于梳状函数的理想取样与实际取样有差别.

下面分析推导矩形脉冲取样后，取样信号的频谱与原始连续信号频谱的关系.取样脉冲序列s(t)是周期性的矩形脉冲信号，因此频谱密度函数为

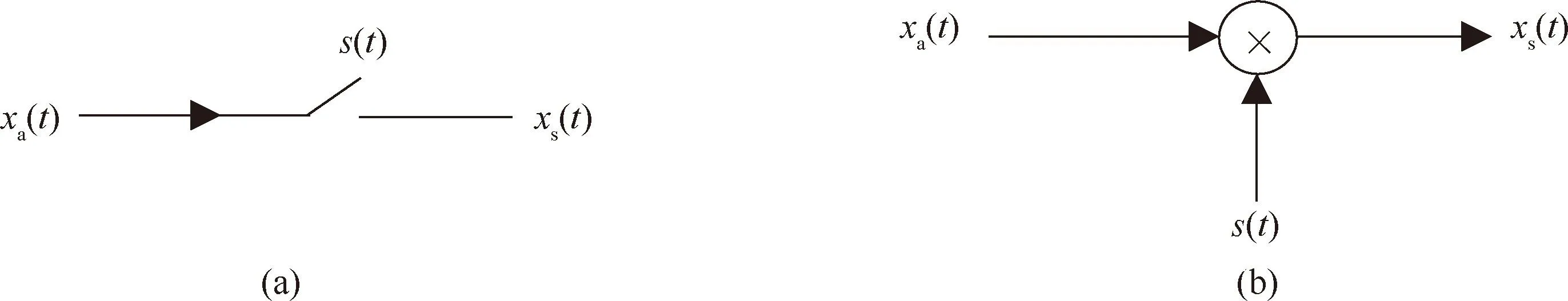
图1 连续时间信号的开关电路和取样模型

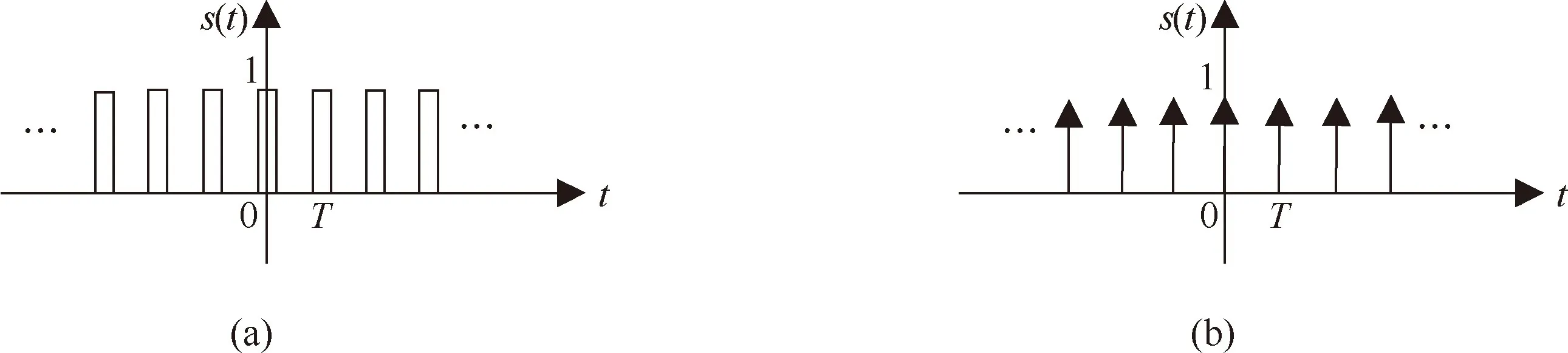
图2 开关函数

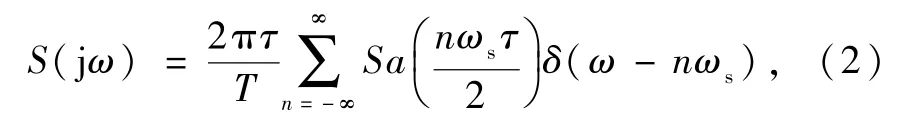
根据傅里叶变换的频域卷积定理，得取样信号的频谱为

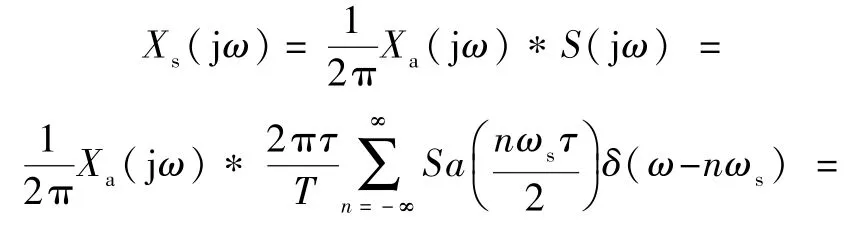
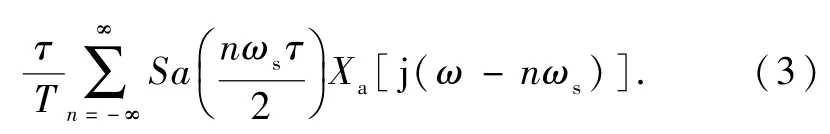
由此可见，连续信号经矩形脉冲取样后，频谱以ωs为周期进行了周期延拓，同时幅度具有Sa(x)函数的包络形式，如图3所示.可以看出，当ωs≥2ωm时，矩形脉冲取样信号的频谱不会发生混叠现象.尽管周期延拓后频谱的幅度按照Sa(x)函数包络线衰减，但是仍可以利用低通滤波器恢复原始信号的频谱.

图3 矩形脉冲取样

2 离散信号与原始连续信号频谱的关系

传统教材中推导原始连续时间信号与取样信号之间频谱的关系，往往忽略了取样得到的离散信号的频谱.针对这一问题，本文对取样得到的离散信号的频谱进行推导，阐明原始连续时间信号xa(t)的频谱与离散信号x(n)的频谱之间的关系.设xa(t)的频谱密度函数为Xa(jω)，则根据傅里叶逆变换，得:

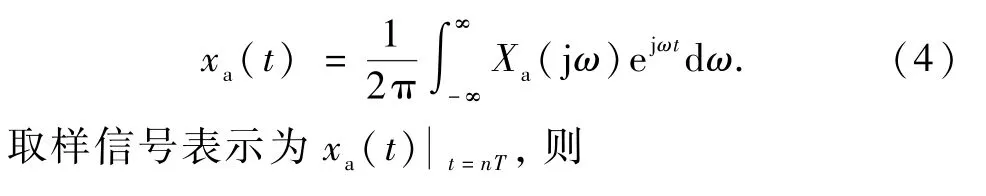
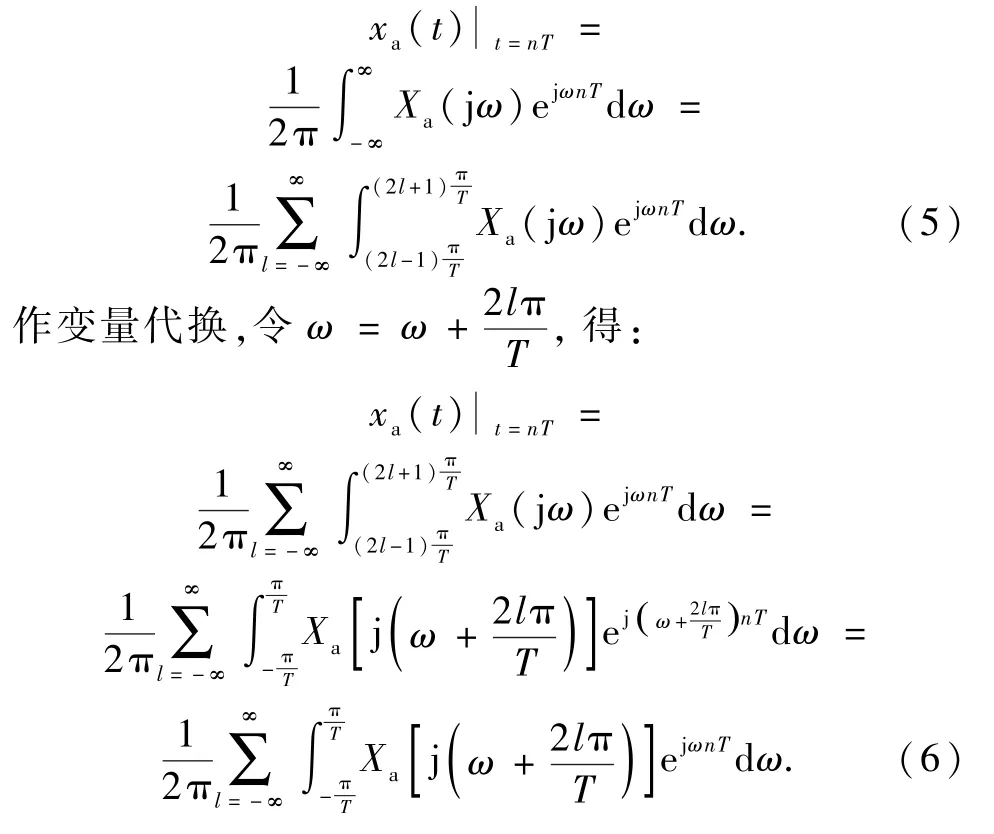
根据数字角频率与模拟角频率的关系，即θ=ωT，上式进一步表示为

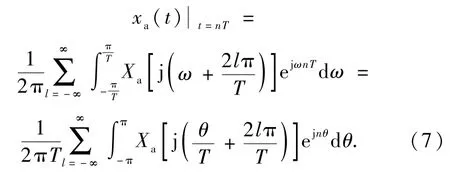
设x(n)的频谱密度函数为X(ejθ)，则根据离散时间傅里叶逆变换，得:

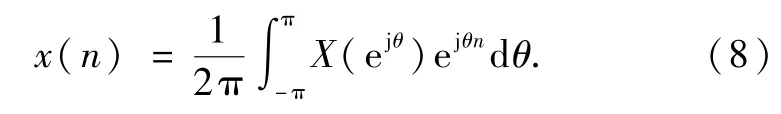
根据信号的时域取样关系，得:

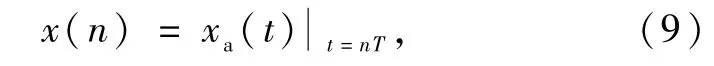
将式(7)和(8)带入式(9)，得:

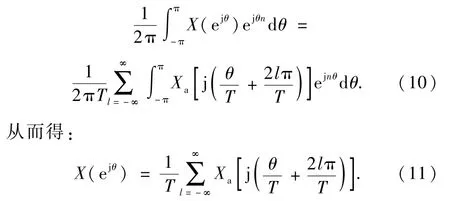
上式表明，离散信号x(n)的频谱相当于对原始连续时间信号的频谱以2π为周期进行了周期延拓，同时按照因子(1/T)进行了尺度变换.对取样信号进行傅里叶变换，得:

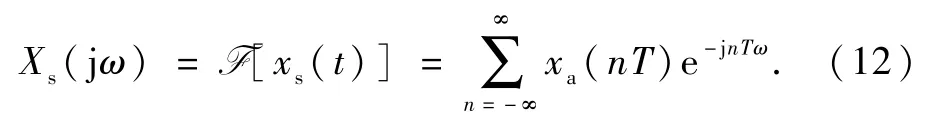
从而得出离散信号x(n)的频谱密度函数X(ejθ)，可以表示为

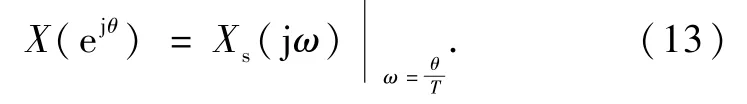
由式(13)可以看出，离散信号x(n)的频谱密度函数X(ejθ)可以看作取样信号xs(t)的频谱Xs(jω)在频率域作了尺度变换，也可以看作对频率轴进行了归一化处理.上述推导表明:从连续时间信号xa(t)到离散时间信号x(n)存在一个时间归一化的问题，对应的频谱密度函数之间也存在着频率归一化问题.

3 抗混叠问题

取样定理阐明:取样信号的频谱以取样角频率为周期进行了周期延拓.因此，为了避免频谱混叠，原始连续信号应是频带有限信号.同时，取样角频率应大于2倍的信号最高截止频率.然而，在实际的工程应用中，取样角频率太大就意味着取样周期足够小，从而造成取样样本点数太大，此时系统需要处理的运算量会相应提高.而且输入的连续时间信号可能不是带限信号，或者输入信号是带限信号但是截止频率太高.比如，在语音信号处理中，通常语音信号的频带范围是4～20 kHz，然而，从语义的可懂性角度来讲，3～4 kHz的频带范围就足够了.而且，信号在传输和处理过程中不可避免会受到噪声的干扰，而噪声往往出现在高频区域，采样后，噪声信号会混叠到低频区域.基于以上因素，工程应用中在采样前会加入一个低通滤波器对输入信号进行预滤波，此时的低通滤波器常称为抗混叠滤波器，如图4所示.在信号取样前，先进行抗混叠滤波，从而可以有效地避免取样过程中的混叠现象.

图4 连续信号的数字信号处理

抗混叠滤波器应具备低通滤波的功能，理想情况下，抗混叠滤波器的频率响应表示为

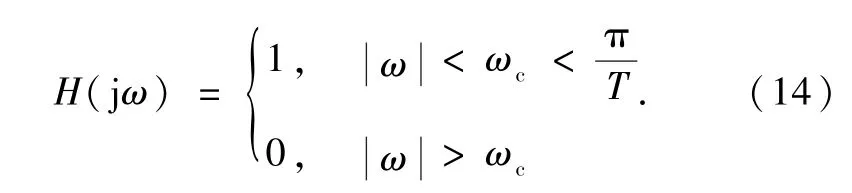
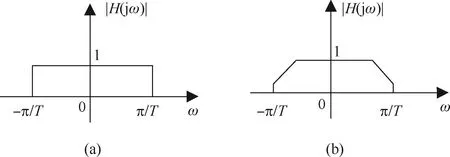
图5 抗混叠滤波器的幅频特性曲线

4 结束语

本文针对目前高等院校开设的《信号与系统》《数字信号处理》《通信原理》等电子信息类课程中，关于取样定理推导过程及工程应用存在的问题，分析了实际取样中矩形脉冲取样信号的频谱，推导了离散信号的频谱与原始连续信号频谱的关系，并对工程应用中的抗混叠滤波器作了分析和说明.以上3个问题的推导和分析，解决了目前相关教材中存在的问题，对于培养、提高学生综合应用所学知识解决实际问题的能力具有积极作用，同时为相关工程人员和教学人员提供实践指导意义.同时也应该知道，奈奎斯特采样定理对信号的表征是建立于元素级的特征，没有考虑信号的内部结构信息.而自然界中的信号通常具有一定的结构性，如图像信号和语音信号均存在结构冗余、时间冗余、空间冗余等等.如果对信号表征能够基于这种结构性的因素，则采样数目会大大降低.因此，当不满足采样定理时，利用稀疏表征和压缩感知理论也可以表征和恢复数据[12].