两道工序无故障的RGV动态调度模型算法研究
2020-06-17龚忠伟陈景生王姗姗莫文君
龚忠伟 李 璐 陈景生 王姗姗 莫文君
(1.天津工业大学机械工程学院,天津 300387;2.天津工业大学经济与管理学院,天津 300387;3.天津工业大学数学科学学院,天津 300387;4.安徽农业大学资源与环境学院,安徽 合肥 230036)
0 引 言
RGV智能小车是智能加工系统的主要载体,集各种高新技术于一体[1].许多学者对其实用性进行了研究,吴长庆等[2]采用基于双重着色赋时Petri网的小车模型,考虑了有轨制导车辆(rail guided vehicle,RGV)的实时调度;甘剑锋和周晓光[3]利用排队论的思想,对自动化立体仓库AGV调度效率进行了分析;陈华和孙启元[4]则在禁忌算法的基础上,研究了RGV出入库的分派策略.
已知智能加工系统的组成与作业流程,智能加工系统由1台带机械手和清洗槽的RGV、8台计算机数控技术(computerized numerical control,CNC)、1条RGV直线轨道、1条上料传送带和1条下料传送带等附属设备构成.RGV可以根据指令控制移动的方向和距离,同时自带1个机械手臂、2只机械手爪和物料清洗槽,完成上下料及清洗物料等任务.具体的系统加工图如图1所示:
1 两道工序无故障的分析
在两道工序加工物料的情况下,每件物料的第一道和第二道工序分别需要由2台不同的CNC依次加工完成,并且在加工过程中CNC安装的刀具不可以进行更换.由于不同组生料在进行第一、二道工序加工时所花费的时间不同,需要确定CNC进行第一、二道工序的数量比.假定已知不同组物料分别进行第一道和第二道工序的加工时间,便可利用物料分别进行第一道和第二道工序的加工时间比来确定CNC进行第一、二道工序的数量比.
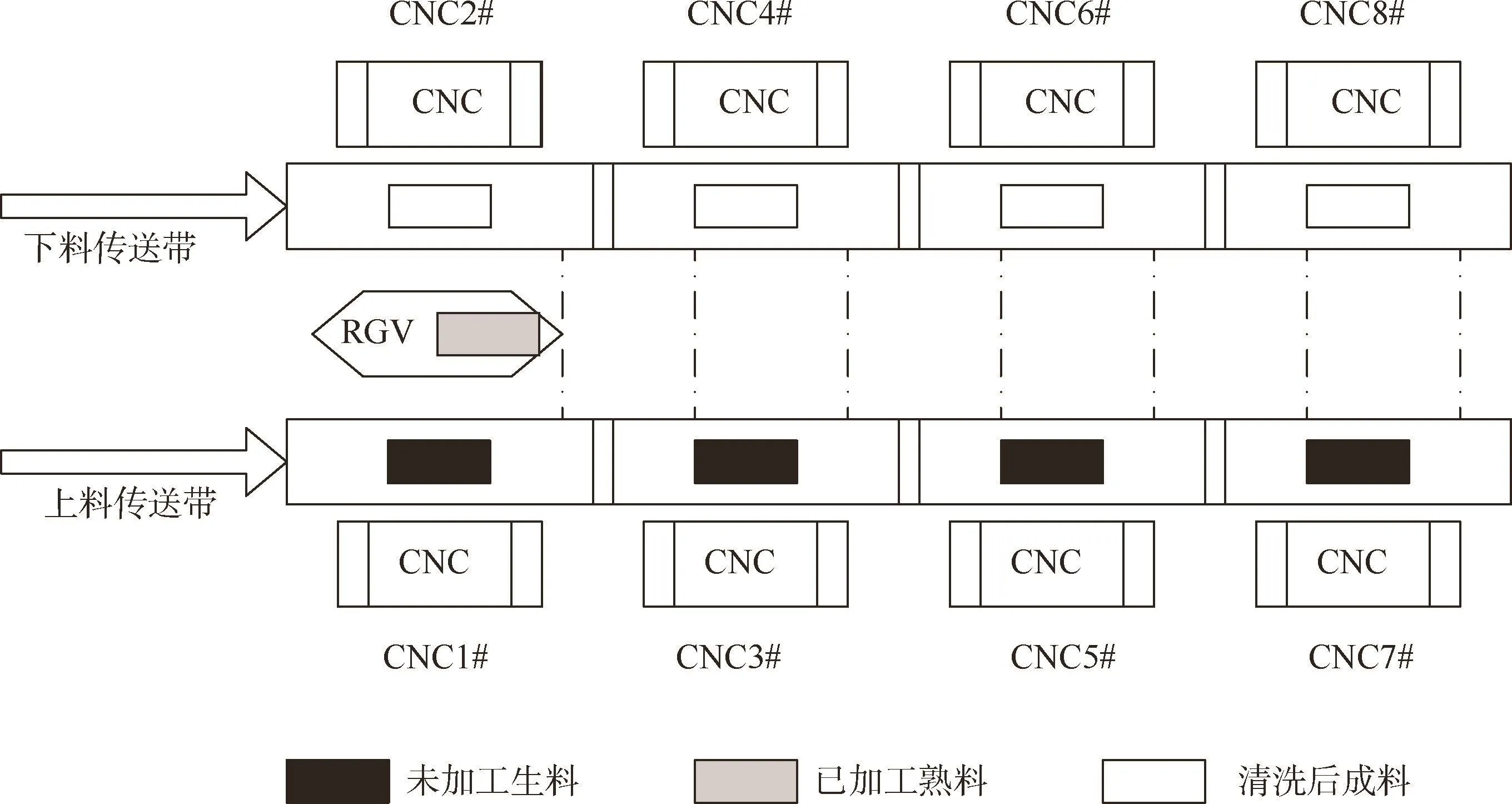
图1 智能加工系统的示意
设第k组物料经过CNC完成一道工序的加工时间为,第k组物料经过CNC完成二道工序的加工时间为,则智能加工系统上第一、二道工序CNC分配的数量比为:
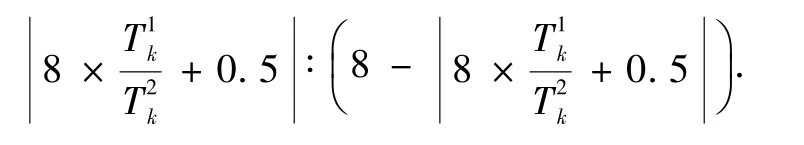
由此便可计算出第k组物料在智能加工系统上第一、二道工序CNC分配的数量比(表1).

表1 不同组物料所使用第一、二道工序的数量比
建立将工序具体分配到CNC上,并给出每个CNC搭配关系的优化模型,使得整个智能加工系统可以在8 h内生产的熟料数量达到最大值.
为确定每台CNC匹配加工物料的工序,可采用以下步骤:
首先,将智能加工系统上第一、二道工序CNC分配的数量比表示为m:n,且m+n=8.
其次,优先将位置相对、序号相邻的CNC分别分配或匹配为工序1和2,即可得到对工序i,i=1,2的加工时间.
最后,计算与之对应CNC的上下料时间(Tsxij)之和,遍历匹配得出,此时第j台CNC对应的加工工序i即为最佳的分配结果.由此便可得到各组物料在智能加工系统中的相应的CNC对应的工序匹配结果(表2).
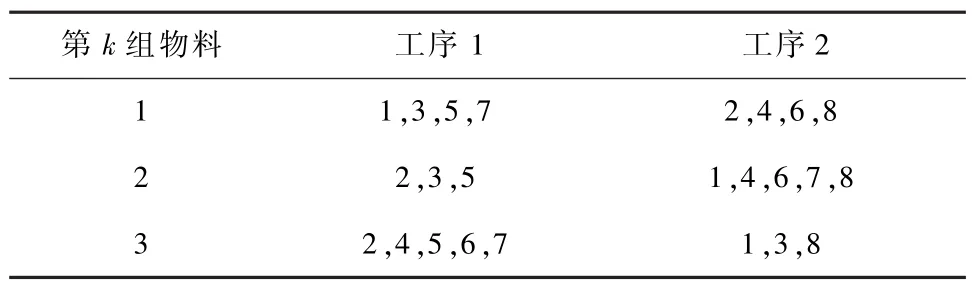
表2 工作台对应的工序匹配
其中ji(i=1,2,j=1,2,…,8)表示第j台CNC完成第i道工序的加工.
通过上述分析得到每个CNC具体分配的工序和CNC对应的工序最佳匹配结果,便可建立优化模型.
2 模型的建立
2.1 目标函数的确定
要实现的目标是,在每班次连续作业8 h中,经过第一道工序成为半成品,再经过第二道工序变成熟料件数的最大值,即:

2.2 同一台CNC加工2件第k道工序的物料的时间间隔约束
考虑到第i个物料在第j台CNC进行第k道工序的时刻为,则1台CNC加工2件第k道工序的物料的时间间隔,必须满足:
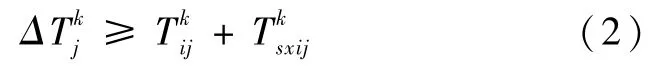
2.3 前后2件物料加工顺序时间的约束
RGV在第j台CNC上对第i件物料进行第k道工序加工后,移动到下一个离其距离最近的已经发出需求信号的第j′台CNC上完成第i′件物料进行第k′道工序加工,若前者刚完成第一道工序的加工,则RGV将去协助进行第二道工序加工;若前者刚完成第二道工序的加工,则RGV将去协助进行第一道或者第二道工序加工.而这2件物料的时间间隔,需要满足:
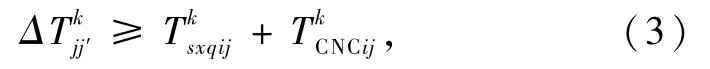

2.4 总时间约束
一个班次为8 h,故有:
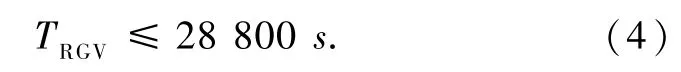
2.5 每件物料完成两道工序完整加工的约束
第i个工件在第j台CNC上完成第一道工序的加工,经过等待后经过上下料,移动到第j′台CNC上上下料,完成第二道工序的加工后,立即向RGV发出信号,整个过程需要满足的时间约束为
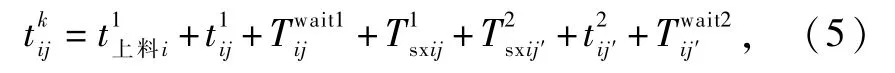

综上所述,可建立两道工序无故障的优化模型为:
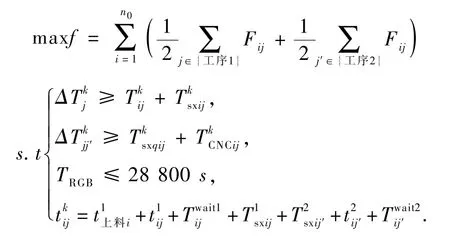
3 模型的求解
3.1 两道工序无故障模型的求解算法
考虑到模型约束条件的复杂性和非线性,将优化模型通过化简,建立动态仿真模型,然后利用仿真的思想进行求解.则两道工序无故障动态模型的具体求解算法如下:
第一步,初始化工作总时间T,从CNCi#移动到CNCj#所花费的时间为TMij,RGV所在位置S=1,CNC1i#用于加工第一道工序,CNC2j#用于加工第二道工序,CNC1i#剩余加工时间(TD1i)=0,CNC2i#剩余加工时间TD2i=0,工作总时间(Total)28 800s,RGV初始状态(Total)0;
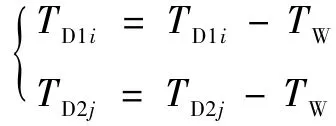
第三步,当Flag=0时,当RGV移动到CNCi#时,CNC1i#的剩余加工时间(Tempi)=TD1i-TMsi,RGV下一个时间段位移耗时(D)={min{TMsi}|Tempi≤0},并更新下一时段位置(S);当Flag=1时,当RGV移动到CNCj#时,CNC2j#的Tempj=TD1j-TMsj,RGV的D={min{TMsj}|Tempj≤0},并更新下一时段S,更新Flag=0;
第四步,更新剩余加工时间TDi=TDi-D,若TDi<0,则使TDi=0.更新总时间(T)=T+D+TSs,其中TSs为RGV在S位置上下料及清洗物料所耗费的时间,若T≥Total,算法结束,否则转到第二步.
3.2 结果展示
通过计算机仿真技术,可以得到一个班次内3组无故障发生时可完成加工的熟料零件数,分别为235、196和240件.
计算得到每个班次内加工物料在不同CNC上进行加工的时间,以第2组参数的加工作业情况为例,选取部分结果,如表3所示:

表3 第2组数据两道工序无故障加工物料时间
4 结束语
RGV智能小车的使用使得仓库管理合理化、存取自动化、操作简便化,可以将本文建立的模型做一些改善,应用到医药生产、汽车制造、机械制造、烟草配送、机场货运、军事等有类似需要物流分配的领域.
