(α,β,λ,λ0,h) 凸函数的 Hermite-Hadamard型不等式∗
2020-06-17时统业曾志红曹俊飞
首都师范大学学报(自然科学版) 2020年3期
时统业 曾志红 曹俊飞
(1.海军指挥学院,江苏 南京 211800;2.广东第二师范学院学报编辑部,广东 广州 510303;3.广东第二师范学院数学系,广东 广州 510303)
0 引 言
作为(α,h)凸函数[1]、m-凸函数[2-3]、(h,m)凸函数[4]、第一种意义上的(α,m)凸函数[5]、第二种意义上的(α,m)凸函数[6]等概念的推广,文献[7]引入了(α,β,λ,λ0,h)凸函数的概念.
定义1[7]设函数f:(0,+∞)→(0,+∞),h:[0,1]→(0,+∞),若存在λ0∈(0,1]及非零实数α,β,使得对任意x1,x2∈(0,∞)和任意λ∈[0,1],有

则称f是(0,+∞)上的(α,β,λ,λ0,h)凸函数.
当β>0(β<0)时,式(1)等价于
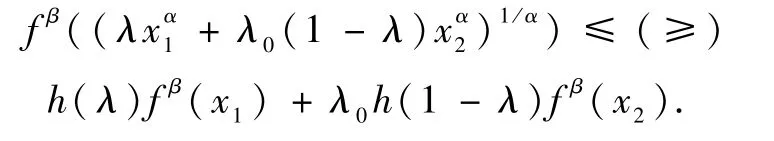
关于各类凸函数的Hermite-Hadamard型不等式可参考文献[3,8-14].本文目的是建立(α,β,λ,λ0,h)凸函数的Hermite-Hadamard型不等式.


1 主要结果





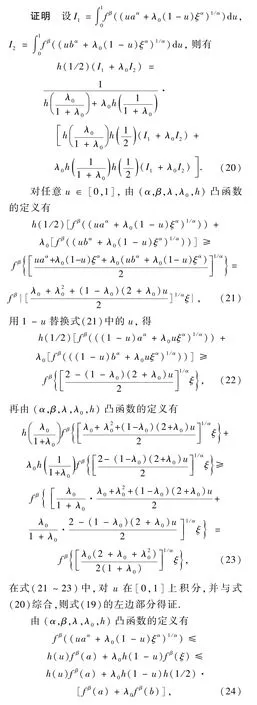




猜你喜欢
——丘成桐
