带可更换阻尼器的波形钢板剪力墙抗震性能试验研究
2020-06-17
(西安建筑科技大学土木工程学院,陕西西安,710055)
作为多高层钢结构建筑的抗侧力构件,钢板剪力墙由约束边缘构件和内嵌钢板组成[1],内嵌钢板与约束边缘构件通过焊接或栓接连接成整体。钢板剪力墙现采用的内嵌钢板形式大多为平钢板,其存在屈曲荷载较低、平面外刚度较小、滞回曲线捏缩等缺陷。波形钢板目前更多地应用于梁腹板,应用于剪力墙中的内嵌钢板的受剪性能类似于梁腹板,内嵌钢板以拉力带的形式承受剪力,而内嵌钢板的形状为波形可以有效提高内嵌钢板的平面外刚度,抑制其平面外鼓曲[2-4]。近年来,建筑结构的设计思想已经由抗倒塌设计向可修复设计转变[5-6],以实现建筑在震后最快的恢复结构的正常使用,可恢复功能剪力墙成为研究的热点[7],其实现方法有摇摆结构、自复位以及设置可更换阻尼器[8-10]。金属阻尼器在低周往复荷载作用下具有良好的变形能力、稳定的滞回耗能,被国内外学者广泛研究。徐艳红等[11]提出了一种抛物线外形阻尼器,可有效避免应力集中。许立言等[12]提出的剪切型阻尼器具有良好的变形能力和耗能能力。国内学者对可更换剪力墙进行了相关研究,吕西林等[13]提出带有可更换墙脚构件剪力墙的设计方法。毛苑君等[14]进行了带可更换墙脚构件剪力墙的低周反复加载试验。刘其舟等[15]提出一种带可更换构件钢筋混凝土剪力墙。目前国内对带有阻尼器的钢筋混凝土墙的抗震性能开展了相关研究,但对带有阻尼器的钢板剪力墙的抗震性能、能否更换阻尼器以及更换后剪力墙再加载的抗震性能的研究较少。本文作者在波形钢板剪力墙的墙趾处开有安置腔,用阻尼器代替原先的墙趾部分,对更换阻尼器前后的剪力墙进行了2次低周往复加载试验,从试件的破坏过程、抗侧承载力、变形能力、刚度退化等方面分析带有阻尼器的波形钢板剪力墙的抗震性能,以期为今后该结构形式的剪力墙的工程应用和研究提供设计依据。
1 阻尼器的设计
1.1 阻尼器构造
本试验设计2种阻尼器,命名为水平波形软钢阻尼器(CMSD-1)和竖向波形软钢阻尼器(CMSD-2),由上下端板、波形腹板和翼缘板组成,上下端板厚为20mm,采用Q235B普通钢,腹板和翼缘板厚为6mm,采用BLY160低屈服点钢。阻尼器的腹板和翼缘不焊接,预留1 cm的空间以充分发挥波形板的面外变形的特点,阻尼器构造如图1所示。
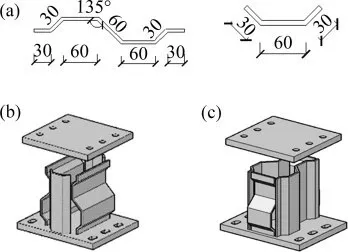
图1 阻尼器构造Fig.1 Construction of damper
1.2 试验研究
试件CMSD-1的翼缘板底部先产生屈曲,形成弯曲变形,如图2(a)所示。在加载初期,试件处于弹性阶段,初始刚度较大,变形较小,滞回曲线接近直线;试件屈服后,试件刚度开始降低,残余变形也逐渐增加,腹板底部和顶部产生应力集中现象,相继产生疲劳裂缝,裂缝产生后试件的刚度退化,承载力迅速下降,试件随之破坏,其残余变形如图2(b)所示。滞回曲线整体形状为梭型,曲线饱满,耗能性能好,如图3(a)所示。

图2 阻尼器试验现象Fig.2 Test phenomenon of damper
试件CMSD-2的腹板沿波折方向的刚度以及翼缘的抗弯刚度均较小,腹板底角处由于应力集中产生裂缝,试件屈服状态时如图2(c)所示。随着荷载的增大,腹板角部塑性变形累积,在距下端板约10mm处产生疲劳裂缝,随着裂缝的开展,试件的刚度和承载力下降,试件破坏,其残余变形如图2(d)所示。试件CMSD-2滞回曲线形状成弓形,且存在捏拢现象,如图3(b)所示,这是因为腹板沿其对角线方向形成抗剪拉力带传递水平荷载,试件CMSD-2承载力和刚度均比试件CMSD-1的高,但延性比试件CMSD-1的差,如图3(c)和表1所示。
2 带阻尼器的剪力墙试验研究
2.1 阻尼器的优化及试件设计
WANG等[16]对波形钢板剪力墙进行了低周往复加载试验研究,确定了波形钢板剪力墙最终在墙趾处形成的塑性区域,故在此区域安装阻尼器。阻尼器的设计要求为:1)保证安装阻尼器的剪力墙的承载能力与原剪力墙相比不过低;2)保证带阻尼器剪力墙的变形模式为阻尼器先于墙体屈服;3)保证阻尼器可以充分耗能。
故本次试验前对选用前文2个阻尼器以及不带阻尼器的剪力墙进行有限元预分析,分析其是否满足上述剪力墙内用阻尼器的3条设计要求,再针对本次试验的波形钢板剪力墙内使用的阻尼器进行优化设计。有限元预分析的模型编号如表2所示。模型示意图如图4所示,3个模型的滞回曲线如图5所示。
本次试验设计的带有可更换阻尼器的波形钢板剪力墙(corrugated steel plate shear wall with damper,简称为CSPSW)采用1:2缩尺模型,轴压比为0.15,墙体高度为1 978 mm,宽度为1 300mm,剪跨比为1.5。内嵌钢板横截面为波形,厚度为3mm,波角均为45°,约束边缘构件-方钢管的厚度为5mm,外边缘长×宽为150mm×150mm。试件CSPSW上下焊接H型钢梁,顶梁高×宽×翼缘厚度×腹板厚度为244mm×175mm×7mm×11mm,底梁高×宽×翼缘厚度×腹板厚度为294mm×200mm×8mm×12mm,钢梁的腹板上均设置不同数目的加劲肋,以增大其刚度和稳定性。阻尼器的上下翼缘板与约束边缘构件以及底梁的连接板通过螺栓采用统一的预紧力连接。
从图5可以看出:Model-2与Model-1相比,Model-2承载力下降多,这是因为阻尼器腹板为横向波形时,腹板平面外刚度几乎为0,受压易发生失稳,说明横向波形阻尼器不满足阻尼器的第1条设计要求;Model-3与Model-1相比,承载力满足要求,但阻尼器应力较内嵌波形钢板小,翼缘无应力变化,且阻尼器变形不明显,如图6所示,说明阻尼器的刚度过大,无法充分发挥阻尼器的耗能能力,不满足第2条,但Model-3整体耗能能力明显比Model-1的强。故对本次研究所用阻尼器进行优化设计,优化如下:由于在阻尼器的拟静力的试验中,竖向波形钢板阻尼器的翼缘无明显变形,且加载结束时,翼缘绝大部分区域未达到屈服,所以,去除其翼缘,并对阻尼器的刚度进行削弱,优化后阻尼器的构造示意及带有阻尼器的波形钢板剪力墙如图7所示。
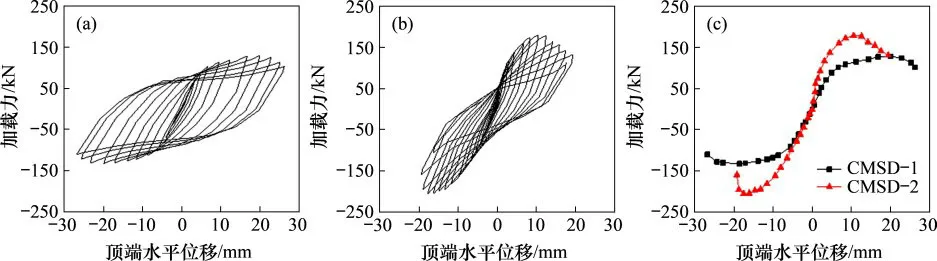
图3 阻尼器的滞回曲线、骨架曲线Fig.3 Hysteresis curve and skeleton curve of damper

表1 阻尼器特征值及延性系数Table1 Eigenvalue and ductility coefficient of damper

表2 模型编号Table2 Number of dampers
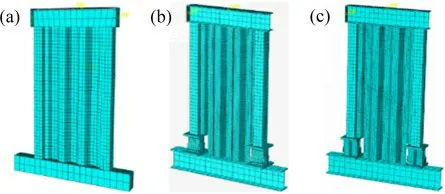
图4 剪力墙的有限元模型Fig.4 Finiteele mentmodel of shear wall
2.2 材性试验
材性试验在西安建筑科技大学的电液伺服万能试验机上完成,内嵌波形钢板和约束构件所用钢材为Q235级钢,材料的力学性能采用金属板材拉伸试验测得,材性试件是按照GB/T 2975—1998“钢及钢产品力学性能试验取样位置及试件制备”[17]的规定从试验的母材中切得并加工成材性试件,材性试验根据试件的位置分为3组,每组试件为3个,钢材的基本力学性能如表3所示。
2.3 加载装置与加载制度
试验地点为西安建筑科技大学结构与抗震实验室,试验采用拟静力加载方法,在加载梁顶部放置分配梁,竖向集中荷载由竖向油压千斤顶施加在分配梁中心,由MTS电液伺服加载作动器对试件施加低周反复水平荷载,作动器一端与反力墙相连,另一端与剪力墙加载梁的西侧相连,底梁两端通过压梁锚固,限制试验中底梁的位移,防止其滑动。
试验加载制度采用荷载-位移双控制加载,试件弹性阶段采用荷载控制加载,每级50 kN,试件达到屈服之后,采用位移控制加载,并以屈服位移的整数倍作为幅值,每一级位移循环3次,根据GB 50011—2010“建筑抗震设计规范”[18]规定的多高层钢结构以及抗震剪力墙结构在弹塑性阶段允许的最大层间位移角,本文规定试件加载至其位移角为1/100时,更换阻尼器且再次对试件进行低周往复水平荷载加载,采用荷载-位移双控制加载,荷载幅值每级25 kN,以便详细的记录试验现象。试验加载到试件的极限承载力下降至85%停止加载。试验加载装置示意和加载制度如图8所示。
2.4 试件CSPSW试验现象
本次试验规定推力为正,拉力为负。
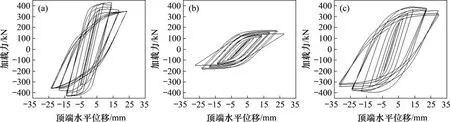
图5 剪力墙的有限元模型滞回曲线Fig.5 Finite element model hysteresis curves of shear wall
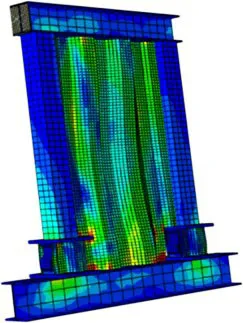
图6 Model-3应力云图Fig.6 Stress cloud ofModel-3
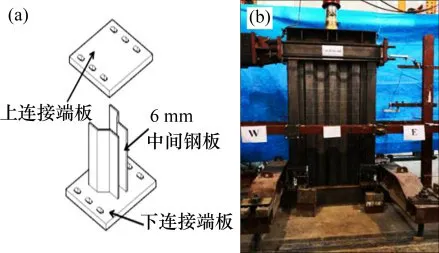
图7 优化后的阻尼器构造及试件CSPSWFig.7 Construction optimized damper and specimen CSPSW
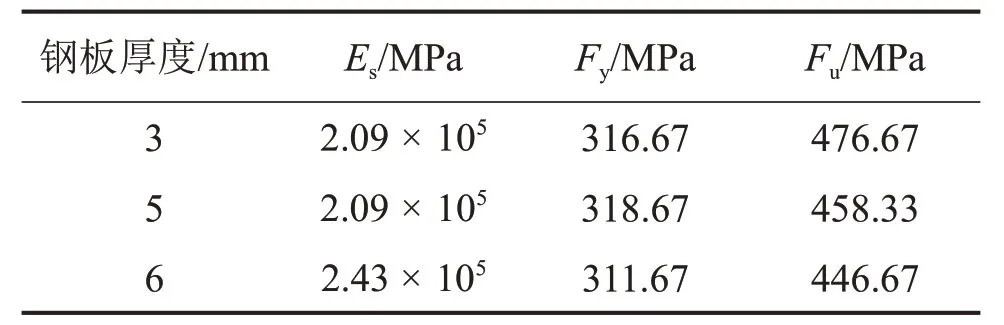
表3 材料力学性能Table3 Mechanical properties of materials
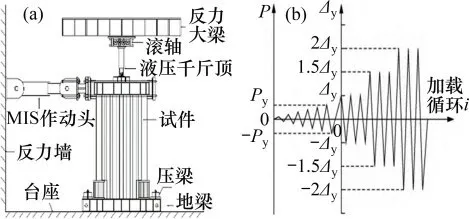
图8 加载装置和加载制度Fig.8 Loading device and loading system
第1次加载:试件CSPSW在施加竖向荷载和预加反复水平荷载的过程中,试件均处于稳定的弹性状态,试件未发生变形。加载至150 kN时,阻尼器腹板外侧发生略微鼓曲,如图9(a)所示。加载至300 kN时,阻尼器的腹板发生明显屈曲,内嵌钢板角部发生略微变形,如图9(b)所示。此时,观察到试件的荷载-位移曲线明显偏离直线,表明构件开始屈服,屈服位移为10.2mm,加载由荷载控制转为位移控制,每级位移推拉循环3次。随着位移的增大,阻尼器腹板向外继续鼓曲。加载至1.5Δy时,西侧阻尼器阻尼器腹板内侧呈S型变形,底部变形扭曲明显,如图9(c)所示。此时试件还未达到极限承载力,位移角接近1/100,此时停止加载,更换阻尼器。
第2次加载:采用荷载-位移双控制法进行加载。加载至-125 kN时,西侧阻尼器腹板中部向外发生略微鼓曲,如图9(d)所示,加载至+300 kN时,荷载-位移曲线出现明显偏离直线的现象,试件屈服,改用位移加载,屈服位移为9.1mm。加载至+1.5Δy,东侧阻尼器腹板外侧鼓曲约6mm,内侧上部向南方向平行屈曲约2mm,中部亦发生鼓曲变形,加载至-1.5Δy,西侧阻尼器南侧腹板发生较大变形,出现S型鼓曲,如图9(e)所示。随着位移的增大,阻尼器的变形逐渐加剧,当水平位移加载至2Δy时,阻尼器整体发生变形,阻尼器最终的破坏形态如图9(f)所示。
2.5 试件CSPSW滞回曲线
图10所示为试件CSPSW 2次加载的滞回曲线。从图10可以看出:第1次加载时,试件CSPSW初始刚度较大,进入强化阶段后,试件的滞回曲线存在捏拢现象。其原因是内嵌波形钢板存在水平方向的拉压效应。第2次加载时,试件CSPSW的初始刚度较大,随着荷载的增大,滞回曲线的加载斜率逐渐减小,加载至后期,阻尼器和内嵌波形钢板屈曲耗能,滞回曲线稳定并且饱满,说明试件耗能性能较好,极限承载力相比于第1次加载时略有下降,这是因为更换阻尼器前的试件CSPSW内嵌钢板角部产生微小变形。达到峰值承载力之后,滞回曲线的斜率下降幅度逐渐增大,这是因为阻尼器发生了整体变形,导致试件的刚度下降。
2.6 试件CSPSW骨架曲线

图9 试件的破坏形态Fig.9 Destructive form of testpiece
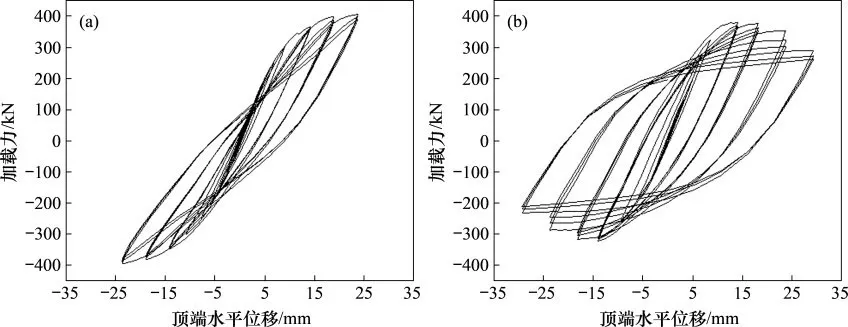
图10 试件的滞回曲线Fig.10 Hysteresis curves of specimen
根据试件CSPSW的滞回曲线,提取试件2次加载的骨架曲线,如图11所示。从图11可以看出:试件2次加载时的初始刚度大致相同,说明更换阻尼器对试件的初始刚度影响不大,母墙的抗震性能仍保持完好,阻尼器可以满足保护主体结构不受破坏或少受破坏的要求。更换阻尼器时试件CSPSW的承载力达到388.97 kN,未达到极限承载力,但骨架曲线上升趋势平缓,已接近于极限承载力。第2次加载时,试件的骨架曲线呈现明显的S形,这说明试件CSPSW在更换阻尼器之后,在水平低周反复荷载作用下,经历弹性、弹塑性、塑性和破坏4个阶段,其极限承载力达到362.68 kN,较第1次加载时略有降低,这是因为试件第1次加载时内嵌钢板角部产生少量残余变形,刚度和承载力有一定程度下降。试件达到极限承载力后承载力下降缓慢,延性较好。
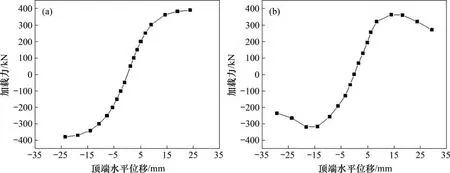
图11 试件的骨架曲线Fig.11 Skeleton curve of specimen
2.7 试件CSPSW延性和耗能能力
由于试件CSPSW第1次加载时,在其层间位移角达到规定值时,试件尚且处于弹塑性阶段,未到破坏阶段,无法完整地考察其延性和耗能能力,故分析试件更换阻尼器后第2次加载时的变形和耗能能力。采用位移延性系数μ[19]衡量试件屈服后变形能力,其计算公式为μ=Δu/Δy,其中,Δu为试件的极限位移,为峰值承载力下降到其0.85倍的荷载对应的位移,Δy为试件的屈服位移。试件CSPSW的特征点如表4所示。

表4 特征点的荷载和位移Table4 Load and displacement of characteristic point
从表4可以看出带有阻尼器的波形钢板剪力墙延性较好。采用等效黏滞阻尼系数[19]ξeq衡量试件的耗能能力,其计算公式为
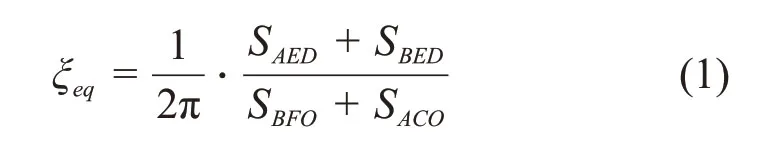
其中:SAED+SBED为滞回曲线所包围的面积;SBFO+SACO为三角形面积之和。
通过计算绘制等效黏滞系数ξeq和位移的关系图,ξeq的计算示意如图12所示,等效黏滞阻尼系数位移曲线如图13所示。从图13可以看出:随着加载的水平位移的增大,等效黏滞阻尼系数呈逐渐增大的趋势。
图12 等效黏滞阻尼系数计算示意图Fig.12 Schematic diagram of equivalent viscous damping coefficient calculation
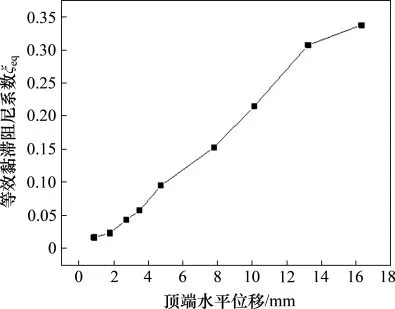
图13 等效黏滞阻尼系数-位移曲线Fig.13 Equivalent viscous damping coefficientdisplacementcurve
2.8 试件CSPSW刚度退化
采用各级变形下的环线刚度[19]K1和位移的关系分析刚度退化,如图14所示,环线刚度K1的计算公式为
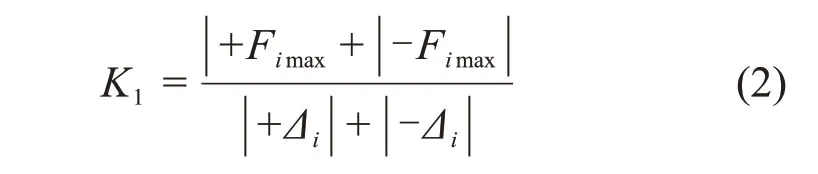
其中:Δi为位移幅值;Fimax为同一位移幅值下,第i次循环对应的力。
从图14可以看出:试件CSPSW承受水平低周往复荷载时,加载初期,刚度降低较缓慢,且推拉出现刚度下降速率不均衡的情况。这是因为在第一次加载完成之时,试件出现了平面外的小变形,并且内嵌波形钢板自身的手风琴效应,试件受拉和受压出现了受力不平衡。
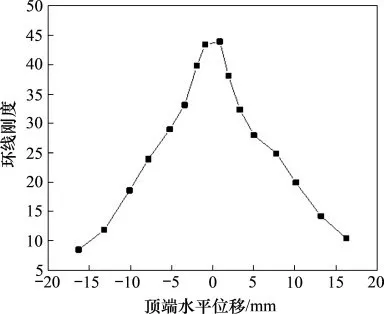
图14 试件的刚度退化Fig.14 Stiffness degradation of specimen
3 有限元分析
3.1 有限元模型
采用ABAQUS有限元软件对试件CSPSW的2次加载进行有限元模拟,模型编号如表5所示。内嵌钢板采用S4R单元,阻尼器和钢梁、约束边缘构件等的单元类型采用C3D8R六面体线性缩减积分实体单元,其中内嵌波形钢板与钢梁和约束边缘方钢管采用Tie连接,阻尼器的腹板与端板之间采用Tie连接。剪力墙和阻尼器的有限元模型如图15所示。由于在第1次加载后,内嵌钢板角部发生残余变形,故第2次加载前利用屈曲模态分析引入初始缺陷,通过对第1次加载结束后内嵌波形钢板角部变形的观察,选取屈曲分析得到的二阶模态的叠加作为模型的初始几何形态,选取的二阶屈曲模态如图16所示。加载制度与试验的加载制度相同,试件第1次加载至位移角为1%,第2次加载至极限承载力下降至其85%。在顶梁上端和侧面均布置刚性体,模拟试验中的加载梁和侧向加载垫块,以使集中力均匀施加。有限元模拟的钢材采用弹塑性等效本构模型,本构模型的取值与材性试验所测得的取值相同。

表5 有限元分析模型编号Table5 Model number for finite element analysis
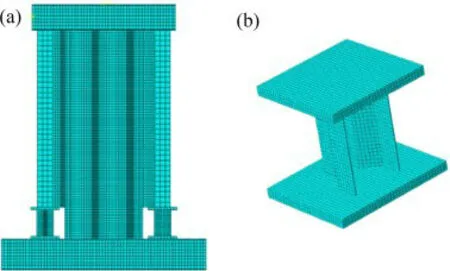
图15 试件的有限元模型Fig.15 Finite element model of test piece
图16 模型CSPSW-B的屈曲模态Fig.16 Buckling mode of model CSPSW-B
3.2 滞回曲线对比
模型与试验的滞回曲线对比如图17所示。
通过对比第1次加载的试件和模型CSPSW-A的滞回曲线可以看出:有限元模型的滞回曲线相比于试验,滞回环更饱满,说明有限元模型的耗能能力更强,这是因为试验中存在着不可避免的误差而导致初始缺陷,而有限元模拟均为理想状态。模型的初始抗侧刚度较大而未能较好地模拟出试验滞回曲线的捏缩现象。
通过对比第2次加载的试件和模型CSPSW-B的滞回曲线可以看出:有限元模型的滞回曲线在模型屈服之后比试验的滞回曲线更饱满,说明其耗能更好,有限元模型的极限承载力亦略大于试件的极限承载力,试验与模型每一级加载滞回曲线的变化趋势大致相同,说明有限元软件能够较好地模拟剪力墙更换阻尼器之后的试验。
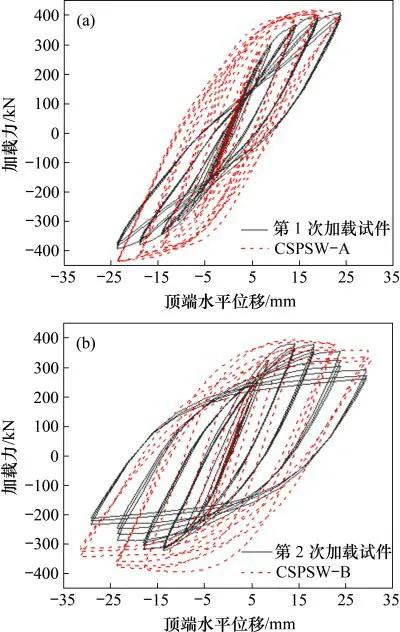
图17 试验与模型滞回曲线对比Fig.17 Comparison of hysteresis curves of test and model
3.3 骨架曲线对比
第1次加载初始阶段,模型骨架曲线的斜率略比试件的大,说明模型的初始刚度略比试件的高,这是因为有限元模型中试件的材料、连接固定均为理想状态。有限元模型加载至位移角为1%时的承载力为402.24 kN,试验结果为388.97 kN,两者较吻合。第2次加载试验的斜率与模型的斜率基本相同,说明模型的初始刚度符合试件的初始刚度。骨架曲线均呈明显的S型,说明两者均经历弹性、弹塑性、塑性和破坏4个阶段,有限元模拟和试验试件的骨架曲线变化趋势相同,试件在倒数第3级水平荷载时承载力开始下降,模型CSPSW-B在倒数第2级水平荷载时承载力开始下降,模型CSPSW-B的承载力较试件的承载力下降较慢,延性更好一些。综上所述,有限元模型的模拟结果同试验结果吻合度较高。有限元模拟和试验试件的骨架曲线的对比如图18所示。
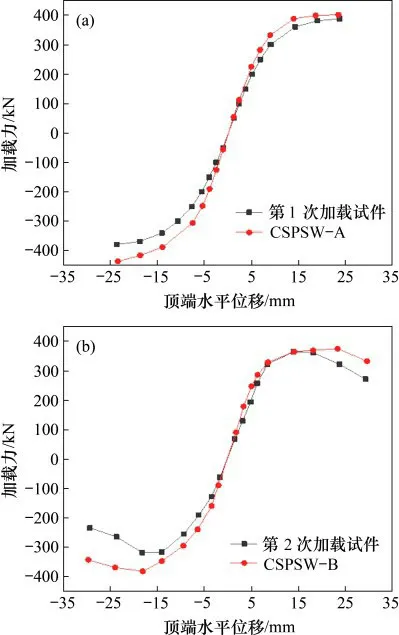
图18 试验与模型骨架曲线对比Fig.18 Comparison of skeleton curves of test and model
3.4 破坏特征对比
试件CSPSW第1次加载时,阻尼器波形腹板外侧首先出现变形,随着荷载的增大,内嵌波形钢板角部出现略微屈曲。通过有限元模型的Mises应力云图的变化可以看出,试件在加载初期,应力先集中在阻尼器的外侧腹板,外侧腹板出现变形,加载后期,波形钢板的下部底角处应力开始增大。
第2次加载在施加水平荷载初期,试件CSPSW和模型CSPSW-B阻尼器腹板外侧下部均先发生屈曲,且随着荷载的增大,屈曲程度增大。随后试件CSPSW和模型CSPSW-B波形钢板的角部均发生变形,然后沿着水平方向应力慢慢向中间发展,内嵌钢板下部发生变形。最终东侧阻尼器两侧腹板中部呈向两侧鼓曲的变形,西侧阻尼器两侧腹板呈向一侧鼓曲的变形。模型同试验的阻尼器最终的变形形态对比如图19所示。有限元模拟的试件在阻尼器更换前和更换后的应力云图对比如图20所示。
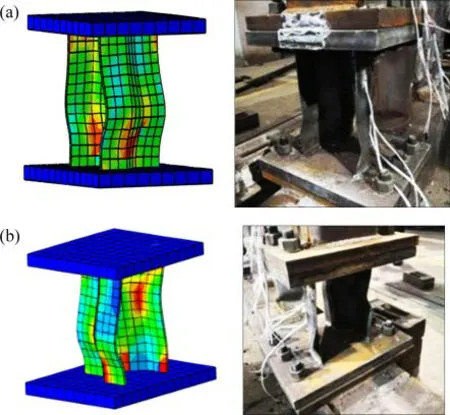
图19 试验与模型阻尼器变形对比Fig.19 Comparison of damper deformation of test andmodel

图20 试验与模型应力云图对比Fig.20 Comparison of stress cloud of test and model
4 结论
1)水平波形软钢阻尼器滞回饱满,耗能能力和延性较好,刚度退化较慢;竖向波形软钢阻尼器承载力较高,初始刚度较大。
2)在剪力墙弹塑性阶段达到规定的位移角时更换阻尼器,阻尼器面外变形明显,发挥集中耗能作用,可以保护剪力墙。
3)带有阻尼器的波形钢板剪力墙初始刚度较大,更换阻尼器后剪力墙滞回稳定且饱满,保持较好的承载能力、延性和耗能能力,刚度退化缓慢。
4)有限元分析结果与试验结果基本相同,说明ABAQUS有限元分析得到的结果可靠性较高,可以为试验和工程实际提供参考依据。
