动压巷道顶板非均匀剧烈变形机理及其稳定性控制

2020-06-17李臣霍天宏吴峥吕坤张兵

中南大学学报（自然科学版） 2020年5期

李臣，霍天宏，吴峥，吕坤，张兵

(1.中国矿业大学(北京)能源与矿业学院，北京，100083；2.煤炭科学技术研究院有限公司安全分院，北京，100013；3.神华神东煤炭集团有限责任公司布尔台煤矿，内蒙古鄂尔多斯，017209)

双巷布置方式能够缓解运输、通风、工作面的接替紧张等问题，但保留巷道(下称留巷)易受到相邻采空区侧向支承压力的影响，维护期长[1-3]，尤其是顶板的剧烈变形破坏严重制约着巷道正常使用，威胁人身安全。针对双巷布置下巷道稳定性问题，众多学者进行了大量研究。在留巷应力环境方面，王书文等[2]基于实测得出采空区侧向53m范围内煤层垂直应力出现不同程度变化；马念杰等[4-7]提出采动应力再分布导致围岩主应力在数值和方向方面均发生较大变化，并主导了塑性区的演化。在留巷变形破坏机理方面，马念杰等[4-6,8-9]提出了巷道非均匀应力场条件下蝶形塑性区理论，并解释了巷道非均匀变形机理；刘洪涛等[10]结合工程现场，通过对主应力、角度和塑性区分布特征的研究，阐明了留巷发生非对称变形的原因；袁越等[11]通过建立并分析深部动压圆形巷道力学模型得出了深部动压回采巷道的变形破坏机理；JIANG等[12-13]通过研究岩体裂隙与刚度的关系得到裂隙破坏对巷道稳定性的影响，并通过数值模拟再现了采动后围岩失稳过程。在巷道围岩控制方面，杨超等[14-15]通过理论分析并结合实验室实验得出低围压状态时围岩的残余强度对支护的依赖性；王卫军等[16-18]通过理论计算、数值模拟等手段研究了锚杆支护阻力对深部采掘巷道围岩塑性区尺寸的控制作用；贾后省等[9,19-20]通过工程实践和理论分析得出现有支护技术条件下无法通过高强锚杆(索)支护来限制软岩巷道顶板下沉量，必须采用高伸长支护材料预防冒顶；姚强岭等[21-22]通过分析巷道含水顶板的失稳机理提出了针对性的控制方案。此外，许多学者通过数值模拟分析进行了巷道工程的设计优化，效果显著，数值模拟分析对巷道工程发挥的愈加明显[23-25]。本文作者针对布尔台煤矿22205辅运巷道顶板剧烈不均匀下沉且多次补强后控制效果依旧不佳的实际情况，从采动应力演化规律及塑型区分布的角度研究采动巷道非对称变形的致灾机理，并分析支护阻力对塑型区的控制作用，最后以矿方现有技术条件为基础，提出针对性的围岩稳定性控制措施，确保本巷道的正常使用。

1 工程概况及动压巷道破坏特征

1.1 工程概况

布尔台矿现主采的2-2煤层回采巷道采用双巷布置，区间煤柱20m，埋深298～383m，平均煤厚3.2m；22205辅运巷设计长度为5 604m，掘宽为5.4m，掘高为3.4m；顶板局部淋水，直接顶为砂质泥岩、粉砂岩，含夹煤层及夹矸，927m处有三维物探断层BF123，巷道采掘平面关系及钻孔柱状如图1所示。自22204工作面采过后，22205辅运巷600～1 600m范围内顶板普遍下沉，局部底鼓，系统锚索补强过4次，局部零星补强，后期补强锚索直径由Φ22型改为Φ28.6型，效果依旧不佳，其中850m处顶板补强支护平面图与现场照片如图2所示。原顶板支护参数如下：锚杆直径×长度为22 mm×2 300 mm，间排距1 000mm×1 000mm，6根/排；锚索直径×长度为22mm×8000mm配合五孔Ω型钢带，间排距2 100 mm×2 000 mm，3根/排。

1.2 动压回采巷道破坏特征

22205辅运巷在受到22204工作面采动影响后，巷道顶板变形严重，主要集中于600～1 600m之间，其破坏特征如下。

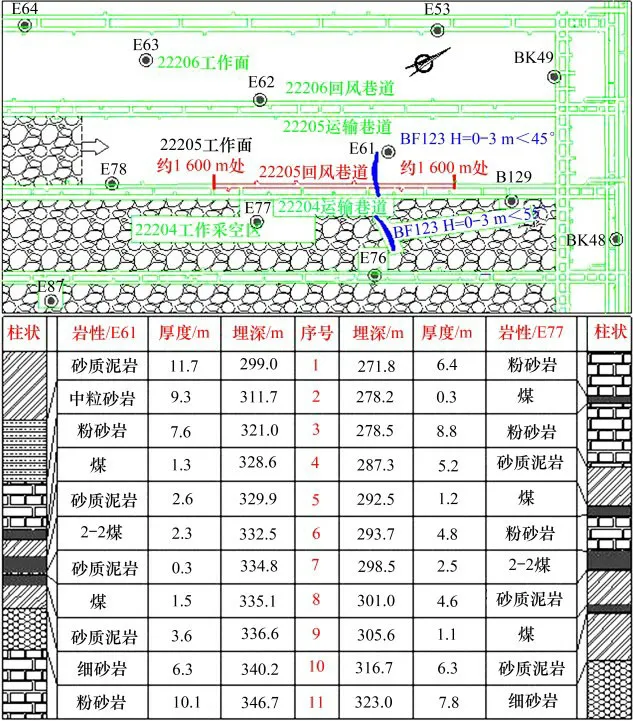
图1 2-2煤采掘平面图及地勘钻孔柱(E77和E61)状图Fig.1 2-2 coalseam mining plan and geological exploration borehole(E77 and E61)histogram

图2 850m处顶板补强支护平面图与现场照片Fig.2 Roof reinforcement support plan and field photos at 850m

1)顶板破碎且下沉量大。巷道受采动影响后顶板下沉量可达400～1 100mm(图2(b)和图3(a)～(c))；顶板岩石破碎(图3(b)～(c))造成巷道顶板剧烈下沉甚至支护体破坏、断裂(图3(d))。

2)巷道呈非均匀性变形。在采动偏应力场影响下，巷道变形呈现整体非对称性(图2(b)和图3(a))，局部台阶下沉(图3(b)～(c))，其破坏属于复合型、“并发症”[11]。

图3 现场实际破坏照片Fig.3 Photos of actual damage at scene

3)围岩破坏范围大。钻孔窥视(下沉量>50 cm)显示：最大破坏深度达到5～6m，顶板4.8～6.0m范围内1m左右的夹煤孔壁粗糙、褶皱并伴有大于10 cm的离层区，破坏明显。孔壁5m以下离层、破碎量占1/3左右(图3(f))，采动围岩破坏范围大。

4)帮鼓及底鼓量大。采动过后在高偏应力作用下，底板会产生非对称底鼓(图3(e))，底鼓严重地段铺设的混凝土开裂损毁，被迫起底返修。

2 蝶形塑性区的力学基础及发育特征

2.1 非等压圆形巷道蝶形塑性区解析式

采空区的应力解除导致其周围一定范围内出现不同程度的应力调整[1]，采动应力分布如图4所示，近采空区附近围岩处于高偏应力状态[4-8]。文献[8]采用圆形孔洞平面应变力学模型获得了非等压均质围岩中圆形巷道围岩塑性区边界方程：

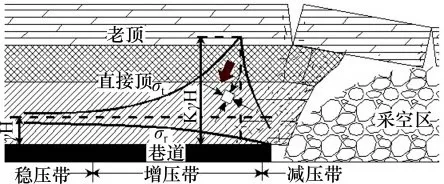
图4 采动应力分布Fig.4 Stress distribution under mining

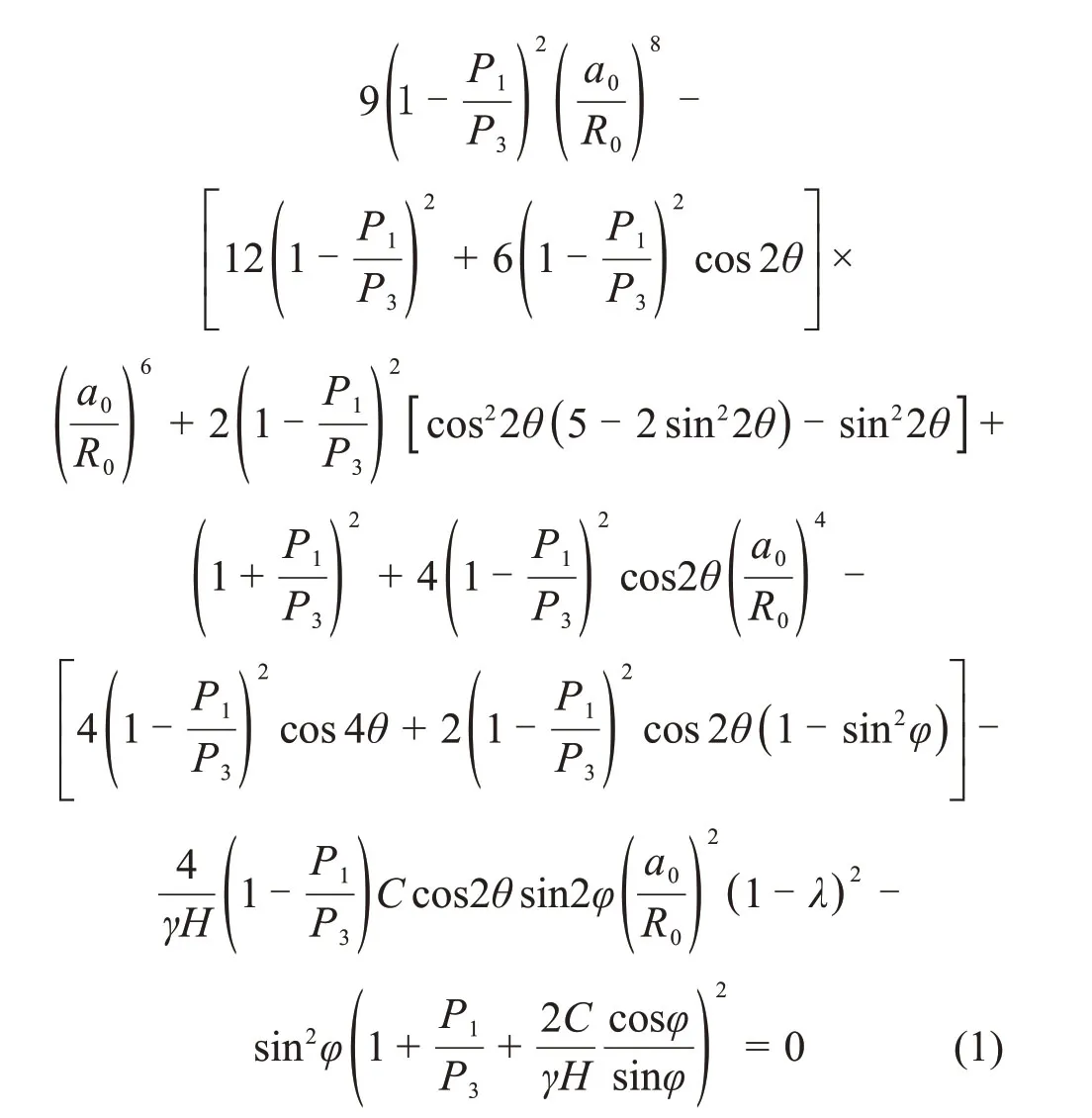
式中：P1和P3分别为最大主应力和最小主应力；a0为巷道半径；R0为径向塑性区边界；θ为任一点极坐标角度；φ为内摩擦角；C为内聚力；γH为巷道竖向载荷。

对于非均质层状岩体巷道塑性区边界不考虑塑性区膨胀变形引起的围岩应力再分布时可将各岩层的参数赋予式(1)计算并叠加，可得到巷道围岩塑性区的等效计算结果[9]。

2.2 蝶形塑性区的发育特征

以布尔台2-2煤巷道围岩力学参数为基础，利用MATLAB编制程序计算埋深300m时双向非等压环境下巷道塑性区边界，塑性区边界与围压比η=P1/P3(布尔台实测侧压系数λ=1.2，即未受采动影响时巷道围压比η=1.2)关系如图5和图6所示。

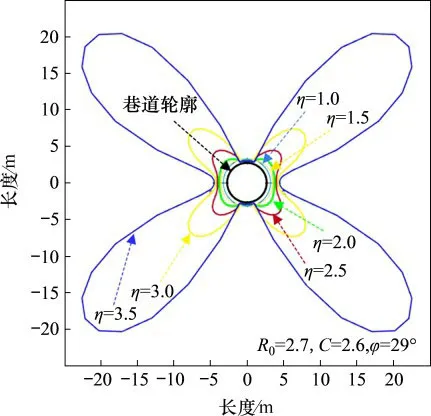
图5 围压比与巷道塑性区对应关系Fig.5 Relationship between confining pressure ratio and plastic zone of roadway

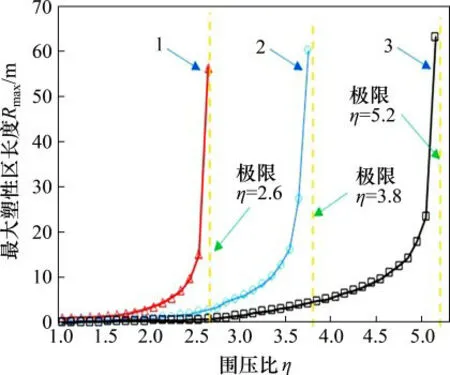
图6 不同岩性围压比敏感性关系Fig.6 Sensitivity of confining pressure ratio of different surrounding rocks

巷道塑性区在η=1时为圆形，随着η增大，塑性区扩展成椭圆形并最终演化为蝶形[6]，蝶叶最大长度Rmax在P1与P3角平分线附近，成蝶后的巷道塑性区范围骤增，将导致巷道失稳，如图5所示。不同强度岩石对η的敏感程度不一致，但成蝶后蝶叶对η的敏感性都急剧增加，表现为Rmax呈指数型增长，曲线突然增大，最终趋于无穷大，如图6所示。

随距采空区距离的不同，主应力方向及大小进行不同程度调整(图4)，从而使主应力不再是垂直、水平方向，因此，P1与竖直方向的夹角α也对应地呈动态变化，但蝶叶始终位于P1和P3角平分线附近，引起巷道蝶形塑性区出现偏转，导致塑性区显现为非对称性[11]。对塑性区公式进行VB可视化编程所获得的蝶形塑性区形态与主应力方向夹角为0°～45°时的对应图如图7所示。

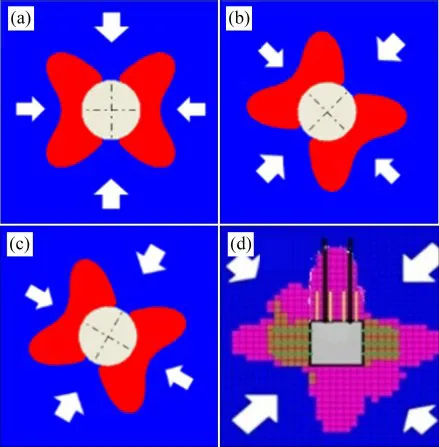
图7 巷道围岩蝶形塑性区形态与主应力方向的关系Fig.7 Relationship between shape of butterfly plastic zone and principal stress direction

3 采动围岩主应力演化规律及留巷塑性破坏特征分析

FLAC是以拉格朗日差分法为基础的数值模拟应用软件，主要应用于岩土工程[25]。结合地勘钻孔E77柱状图及岩石力学参数(表1)对2-2煤进行FLAC3D数值模拟计算，模型长×宽×高为500m×600m×200m(图8)，模型侧面及底面为固定约束，上边界施加5MPa垂直应力，采用Mohr-Coulomb准则，测压系数λ取1.2。

3.1 采动围岩主应力演化规律

在开挖22204工作面450m处，获得其侧方22205辅运巷一次采动影响时的应力分布如图9～11所示。

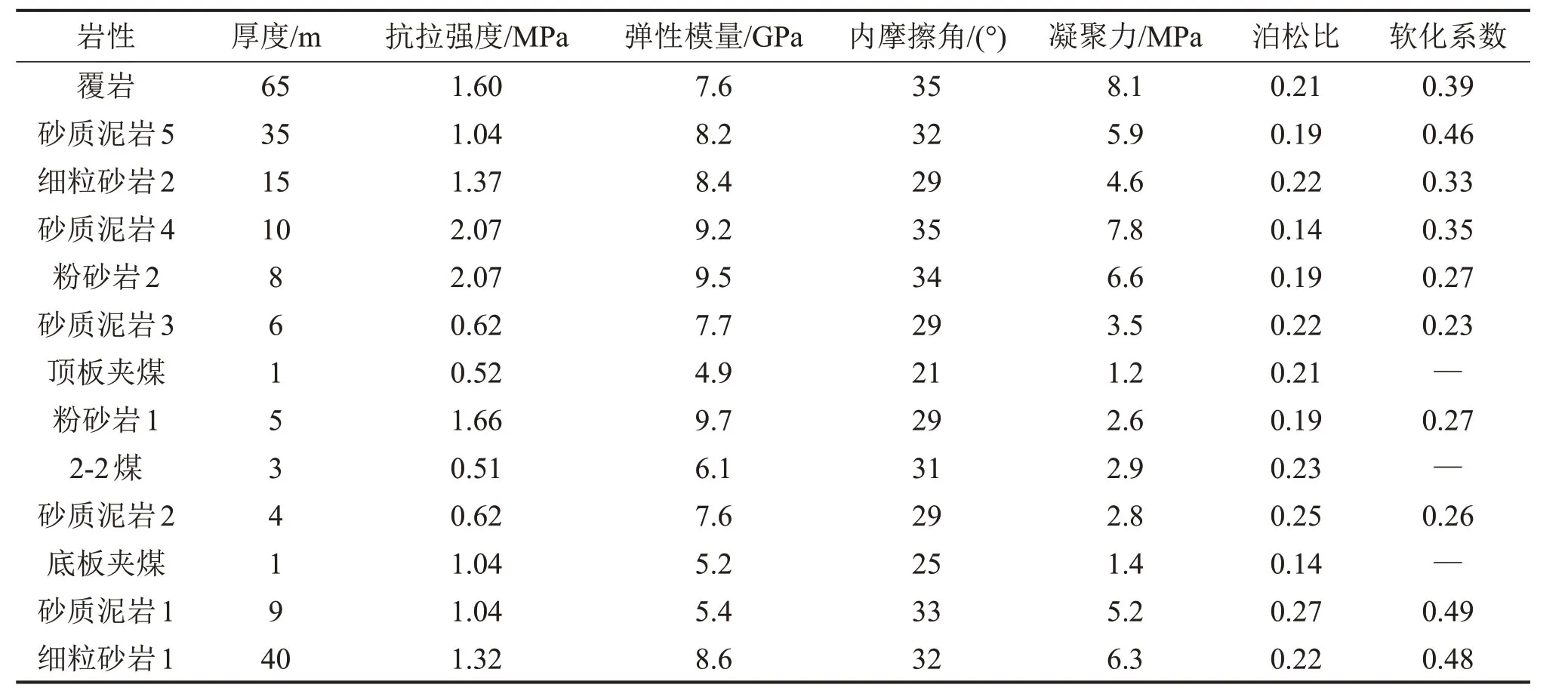
表1 岩石力学参数表Table1 Rock mechanics parameters

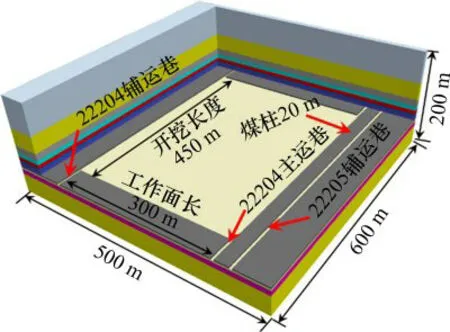
图8 数值模拟模型简图Fig.8 Model diagram of numerical simulation

由图9可知：采空区侧方3～15m范围内，主应力均出现应力集中现象，P1在采空区侧方10～20m呈明显的减小趋势，P3减小趋势则不明显。由图10可知：侧方0～3m主应力急剧增加，3～6m应力降低，6～9m再次增加，这是顶板含水软化后强度小于煤体强度导致应力深部转移量不一致所致；P1在6～9m顶板深部支承压力的影响下煤层再次出现应力峰值，在9～80m范围内，随着距采空区边缘距离增加，应力下降最终趋于稳定，P3在20m后的变化量较小，逐渐趋于稳定。

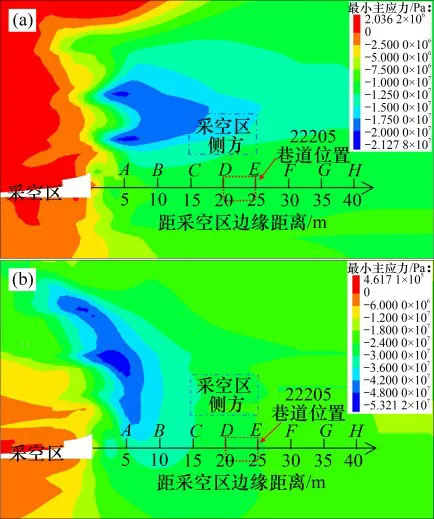
图9 采动侧方主应力分布云图Fig.9 Distribution of principal stress on side of goaf

由图11可知：由于采空区2m内水平泄压和垂直增压导致η极大，侧方1m甚至可达10以上，侧方5m内逐步减小，5～9m时增加，9m时η为3.73，25m时η为2.26，随后，η下降幅度越来越小，并趋于侧压系数λ。与应力分布规律相对应，P1方向与竖直方向的夹角α距采空区4m时为2°，应力偏转88°，此后逐渐减小，距离采空区20m时为60°，应力偏转30°，距离采空区80m时为85°，应力偏转5°，α逐渐接近于原岩应力状态。

3.2 采动围岩塑性区形态特征规律

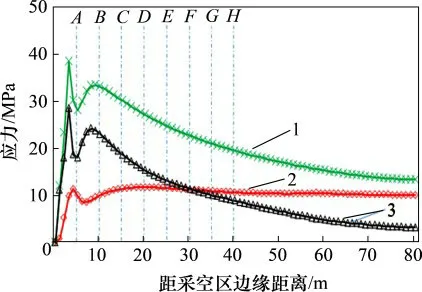
图10 采空区侧方主应力曲线Fig.10 Principal stress curveon side of goaf

为明确采动应力分布对巷道塑性区的影响，建立长×宽×高为50m×1m×50m的巷道模型，岩石力学参数见表1。提取侧方不同位置处(图10和图11中的A～H)的应力进行数值模拟计算，结果如图12所示。

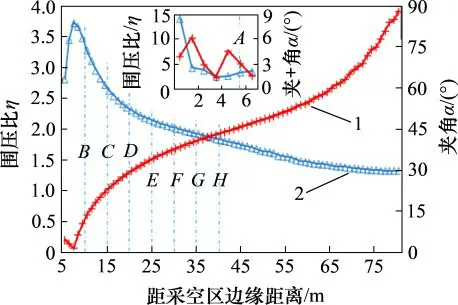
图11 采空区侧方围压比与应力夹角Fig.11 Confining pressure ratio and stress angle on side of goaf

由图12可知：随着距采空区边缘距离的增加，塑性区的形态具有一定规律性；距采空区5m时P1接近垂直应力，α接近90°，塑性区基本为对称状，如图12(a)所示，η=3.73时围压大于围岩的极限围压，导致蝶叶无限扩展，巷道处于蝶形破坏状态。此后，随围岩P1(32.2 MPa→19.0 MPa)及η(3.73→1.79)减小，巷道塑性区逐渐减小，依旧呈蝶形分布，但在α的影响下蝶形塑性区非对称分布，如图12(b)～(h)所示。此外，不同强度围岩对成蝶条件的敏感性不同导致巷道顶底板软弱夹煤出现隔层塑性区，采场开挖后侧方20m煤柱外的巷道塑性区见图13。

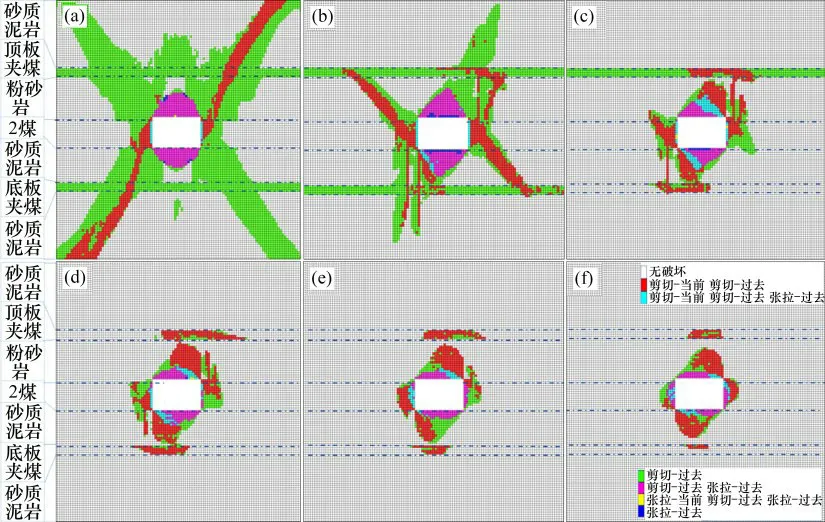
图12 采空区侧方不同距离处巷道塑性区发育形态，Fig.12 Plastic zone of roadway at different distances from side of goaf

按照文献[9]所述计算方法，20m煤柱时巷道所处应力环境主要参数为：P1=27.2 MPa，P3=11.8MPa，α=30°，η=2.31。计算可得本矿巷道塑型区在均质粉砂岩1中R0为4.62m，在均质顶板夹煤中R0为17.24m，由于夹煤在顶板5～6m范围之内，因此，理论计算所得塑型区深度小于粉砂岩1厚度导致隔层在夹煤层中扩展，理论计算结果与数值分析结果(图13)一致。

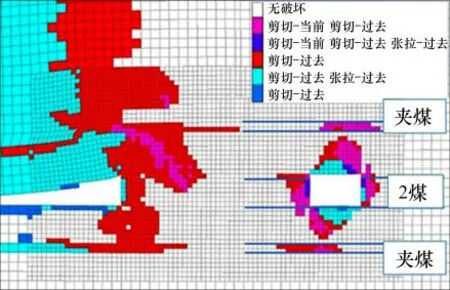
图13 巷道塑性区Fig.13 Plastic zone of roadway

4 支护阻力对塑性区的控制作用分析

4.1 锚杆（索）支护阻力的塑性控制计算

岩体力学已给出圆形巷道塑性区半径公式[26]为

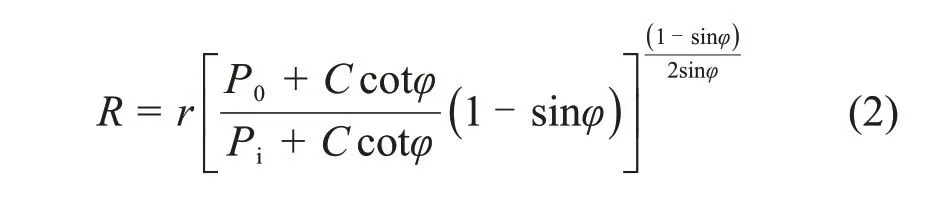
式中：R为巷道塑性区半径；r为巷道半径；P0为原岩应力；Pi为支护阻力；C为内聚力；φ为内摩擦角。

取Pi=0～1.0MPa分析Pi对围岩塑性区的影响。原岩应力P0取7.5，12.5和17.5MPa(对应埋深分别为300，500和700 m)，r=2.7 m，C=3 MPa，φ=27°，得出塑性区半径减少值ΔR随支护阻力增大而增大，但每增加0.1MPa支护阻力对应塑性区半径减少值ΔR的差ΔΔR减小，即敏感性减弱，如图14所示。1MPa支护阻力在r=2.7m的巷道相当于顶板每米至少30根Φ22锚杆或10根Φ22锚索，因此，现场实际的加强支护对控制塑性区作用有限。

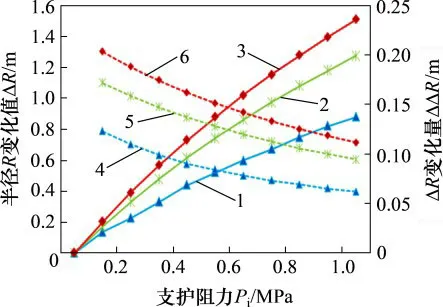
图14 塑性区的支护阻力敏感性曲线图Fig.14 Sensitivity curve of plastic zone to support resistance

4.2 锚杆（索）支护阻力对塑性区控制作用的数值模拟

FLAC3D数值软件将锚杆锚索采用Cable单元进行模拟，其中锚杆/锚索规格按现场实际赋值，锚杆(锚索)锚固长度为1m(2m)，预应力为120 kN(350kN)的设计锚固力，垂直于顶板布置。将巷道位置处(见图11中D点)的应力赋予模型中，以作用力更强的锚索为变量，支护方案如表2所示，研究不同支护强度对顶板塑性区的作用，结果如图15所示。

表2 支护方案表Table2 Form of support scheme

由图15可知：无支护状态时的巷道围岩塑性区为蝶形且非对称，顶板最大破坏深度为4.6m，面积为16m2。当顶板支护锚索密度由3根/m增加到12根/m，即支护阻力由0.33 MPa增加到0.91MPa时，塑性区最大深度由4.6m减为4.4m，仅减少0.2 m，塑性区面积由14.92 m2减小到13.28m2，4种支护密度对顶板塑性区面积的控制率分别为6.75%，9.00%，12.25%和17.00%，塑性区依然呈现非对称性。

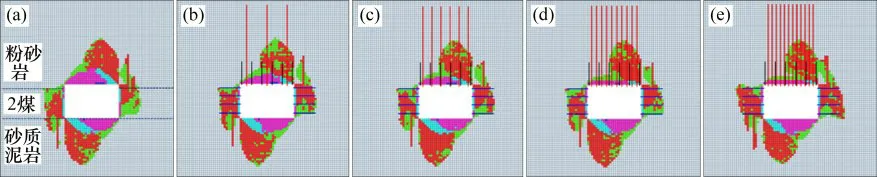
图15 不同支护密度下塑性区分布Fig.15 Plastic zone at different supports

可见，在现有支护水平下，提高支护阻力对减小巷道围岩破坏范围的作用有限[16]，支护作用的实质是将蝶形塑性区内的破坏岩石锚固到塑性区外围稳定岩层，防止围岩失稳冒落，控制非连续性变形[16-18]。

5 非均匀剧烈变形致灾机理及其控制

5.1 顶板非均匀剧烈变形致灾机理

1)围岩强度软化。下沉段地质条件复杂，局部断层发育，顶板邻水普遍，岩石内聚能减小，强度软化[20-21]，导致围岩扩容效应强，承载力下降，稳定性和整体性降低，支护体的可锚性弱化。

2)力学环境的影响。留巷所处应力场为原岩应力、支承压力、开采动载以及塑性区内膨胀压力等组成的极其复杂的叠加应力场[11]；采空区周边应力调整使围岩主应力方向产生不同程度偏转，巷道处于非均匀偏应力场。

3)塑性区蝶形扩张效应。蝶形塑性区由巷道围压比η、应力及围岩岩性决定，属于给定量；不同强度围岩对η的敏感性不同，导致塑性区在巷道顶板隔层扩展，形成潜在冒顶区并释放强烈的变形压力[16]。

4)支护不合理。顶板浅部岩石会产生碎涨现象，并伴随由强大的膨胀压力[9]，锚索延伸量将无法匹配巷道变形而破断，现场后期实际补强的大直径锚索三径不匹配，锚固力远小于破断力，锚索延伸能力未显现就已发生拉脱，作用效果有限。

5.2 顶板剧烈变形段的稳定性控制

考虑到顶板多次补强后的持续下沉及日后22205工作面开采后超前支承压力叠加可能造成的巷道失稳等问题，对该区间进行高分子注浆，在巷道中间施工240个注浆孔，间距为5m，孔深为5m，注浆0.5 t/孔，共注浆120 t。二次采动期间，在巷道超前工作面40m处布置5台ZQL2×22500/22/40D型超前液压支架，预防巷道冒顶。采取措施后取得了一定效果，超前段受二次采动影响虽偶有锚索破断崩出，但整体上保证工作面安全推过本下沉段。

5.3 顶板剧烈变形的稳定性控制建议

在巷道工程现场，很多巷道及时补强后仍然不能有效控制围岩大变形[15]，基于数值分析锚杆索支护对塑性区的控制作用，针对布尔台矿巷道顶板大变形的实际情况，提出以下巷道锚杆锚索支护建议。

对于大变形巷道的“给定变形”，其稳定性控制思路应由变形控制转为防冒灾害控制，具体为：1)允许一定泄压变形但要杜绝冒顶；2)支护体延伸量大于围岩变形量，柔性支护；3)锚索自由段长度大于塑性区最大深度；4)锚索承载力大于塑性区体积质量；5)浅部有一定密度防漏顶；6)下沉量大于锚索可延伸量的70%时及时补强支护，持续提供支护阻力。