电磁驱动二维精密平面运动平台设计与控制
2020-06-17
(中南大学高性能复杂制造国家重点实验室,湖南长沙,410083)
近年来,微纳米定位系统已广泛应用于光电子封装、纳米技术、激光微加工等工程科学领域[1]。在这些领域中,大行程和高定位精度是定位系统的关键参数[2]。特别是随着高容量、多通道的光电器件的兴起,人们对光电子耦合系统的精度要求越来越高[3]。目前,光电子器件耦合系统主要由多个单自由度平台组合而成,而单自由度运动平台可以较容易地实现纳米级的定位精度,但当叠加成所需多自由度系统时,由于存在装配误差、组件对准误差、控制误差等,组合平台难以保持原有定位精度和定位能力[4-5]。此外,在实际应用中,高精度测量和加工平台的性能受Abbé原理的限制[6],这些因素制约了组合平台的发展和使用。通过将平台的X和Y方向运动限制在1个公共平面内,可以完全消除Abbé偏移误差[7],因此,平面运动解耦方式成为近年来国内外研究的热点。AWTAR等[8-9]提出利用材料变形原理设计的柔性铰链或采用传统的刚性铰链来实现运动解耦。MO等[10-11]提出利用空气轴承或磁力使动平台悬浮,或采用平面电机等非接触式驱动部件,实现同平面内多自由度运动解耦。当运动平台要求达到厘米级的运动行程且同时保持微米或纳米级的运动精度时,电磁力作为驱动力是一种可行的方法[12-13]。而新技术的发展降低了永磁线性马达的质量和体积,新的制造工艺和控制策略大大提高了直线电机的性能,给大行程高精度精密运动平台提供了一个新的电机选择[14-15]。同时,在实现微/纳米定位时,需要采用高精度传感器来测量工作台的位移。采用激光干涉原理和光栅尺的测量系统为纳米系统的长位移测量提供了更精确的解决方案[11]。针对传统组合平台的局限性,本文作者提出一种基于电磁力的二维精密平面运动平台。该平台采用1对正交布置的直线电机作为驱动部件,利用1对正交布置的直线轴承将平台的X和Y方向运动限制在同一平面内,同时利用高精度光栅尺实时检测运动位移,保证运动精度。
1 平面运动平台结构设计和分析
1.1 系统结构设计
系统整体结构如图1所示。平台整体采用上下结构,底部为1对正交布置的驱动模组。驱动模组产生的动作通过1对正交布置的直线轴承传递到动平台,实现平面运动。光栅读数头和标尺构成平台的测量系统,其可检测的最小位移为0.1μm。
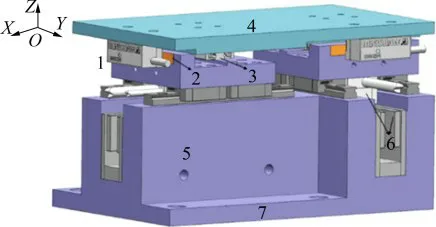
图1 二维精密平面运动平台整体结构示意图Fig.1 Schematic diagram of overallstructureof planar moving platform
图2所示为该平台的解耦原理图。滑块a、滑轨a构成直线轴承a,滑块b和滑轨b构成直线轴承b。滑块a和滑块b通过螺钉与动平台相互连接,导轨a固定在X轴向驱动模组上,导轨b固定在Y轴向驱动模组上。当平台向X方向运动时,X轴向驱动模组带动直线轴承a、动平台和直线轴承b的滑块b运动。同样,当平台向Y方向运动时,Y轴向驱动模组带动直线轴承b、动平台和直线轴承a的滑块a运动。X(Y)轴向驱动模组结构如图3所示,每个轴向驱动模组由永磁体、线圈、直线滑块组和起支撑作用的基板组成。永磁体固定在底座上,直线滑块和线圈通过基板相互连接。当线圈通电时,其在磁场中受到洛仑兹力的作用,带动基板和直线轴承a(b)运动。

图2 解耦原理示意图Fig.2 Schematic diagram of decoupling principle
1.2 直线电机动子的动力学分析
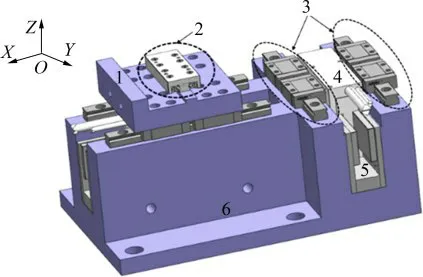
图3 驱动模组结构示意图Fig.3 Schematic diagram of drivemodule structure
每个直线电机通过控制线圈中电流来控制电磁力。由文献[16]知,基于直线电机的运动平台中动子的动力学模型为
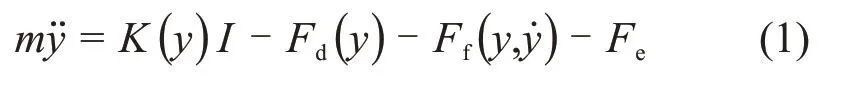
其中:y,和分别为动子的位移、速度和加速度;m为运动体的质量;K(y)为电机的推力系数;Fd(y)为直线电机的定位力;Ff(y,)为直线电机的摩擦力;Fe为电机动子受到的外力负载;I为动子中线圈的电流。
对式(1)进行积分,则可以用下面的函数来表示二维平面运动控制系统的被控对象:
其中:y=[y1,y2]T;y1和y2分别为平台X轴和Y轴向的实际位移;x为与位移y相关的矩阵,xi=u为线圈中电流的输入量,u=[I1,I2]T;I1和I2分别为驱动平台沿X和Y方向移动时对应线圈中电流;d为施加外力负载时对系统的干扰向量,d=[d1,d2];d1和d2分别为X和Y方向上外力负载对系统的干扰值。
2 具有非线性阻尼前馈补偿器的PI控制器设计
平台实现的二维平面运动形式分别为沿X和Y轴向的平移,因此,被控对象即平台包括2个输入和2个输出。假定驱动平台沿X和Y轴向平移的电机线圈中的电流分别为I1和I2,线圈的实际位移y1和y2为动平台的输出量。采用具有非线性阻尼前馈补偿的PI控制器进行控制。运动控制主要包括位置环控制部分、速度环控制部分、电流环控制部分和相应的非线性阻尼前馈补偿器。图4所示为控制系统的逻辑框图,其中,电流环已经集成到直线电机的驱动器中,由其自行调整。因此,控制器的输出可以表示为

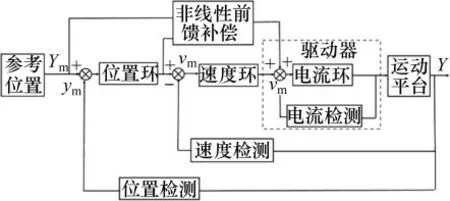
图4 控制系统示意图Fig.4 Schematic diagram of controlsystem
2.1 位置环设计与速度环设计
位置环采用比例控制,数学表达式为

式中:v=[v1,v2]T,v1和v2分别为沿X和Y轴的运动速度;Kp=[Kpy1,Kpy2],Kpy1和Kpy2分别为控制X和Y轴控制器位置环的比例系数;ym=[ym1,ym2],ym1和ym2分别为沿X和Y轴的目标位置。
速度环采用PI控制,其数学表达式如下:
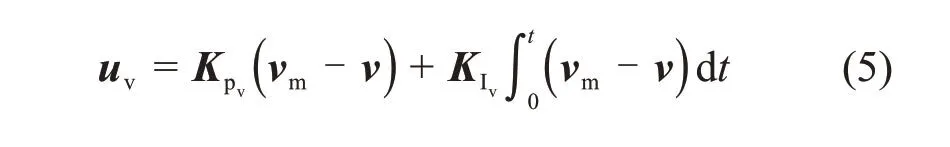
式中:Kpv=[Kpv1,Kpv2],Kpv1和Kpv2分别为控制X和Y轴控制器速度环比例系数;vm=[vm1,vm2],vm1和vm2分别为沿X和Y轴的目标速度;KIv=[KIv1,KIv2],KIv1和KIv2分别为控制X和Y轴控制器速度环积分系数。
2.2 非线性阻力前馈补偿器设计
由式(1)可知,运动平台非线性阻力主要包括摩擦力和定位力,其中,K(y),Fd(y)和Ff(y,y˙)均可以通过实验获得。
1)求取K(x)。使电机处于匀速运动状态,当外力负载分别为Fe1和Fe2时,
根据式(6)可得
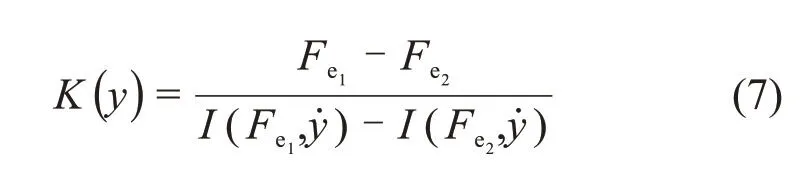
式中:I()和I()为外力负载分别为Fe1和Fe2时线圈中电流输入量。
2)求取和Fd(y)。根据文献[16],当摩擦单元处于滑动状态时,可以采用GMS摩擦模型中的Stribeck曲线定义:
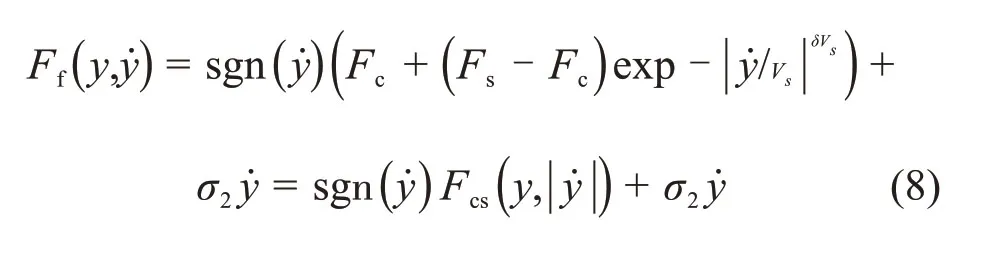
其中,sgn为符号函数。Stribeck曲线随着速度增大而下降,其最大值为静态摩擦力Fs,最小值为库仑摩擦力Fc;Vs为Stribeck速度系数;δ为Stribeck因子;σ2为黏性摩擦因数。
由式(8)可知
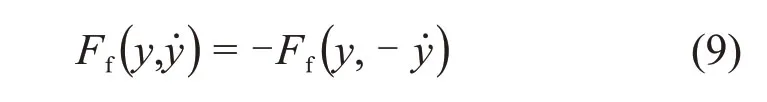
根据文献[14],定位力可以表示为
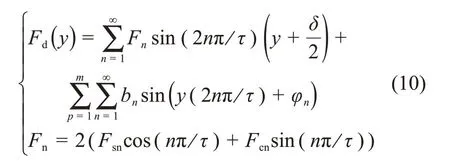
其中:δ=kτ-Ls,k为整数;Ls为动子长度;τ为极距;m为永磁体量,个;φn为各级数相位;bn为第p块永磁体单独作用时的齿槽力;Fsn和Fcn为傅里叶级数中正余弦分量的各次幅值。
根据式(1),给平台施加的外力负载为Fe=0,在动子运动速度为v和-v时,有
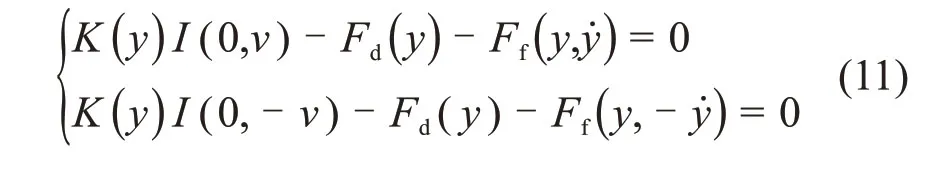
联立式(9)和(11)得
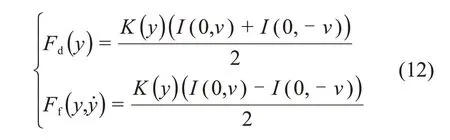
式中:I(0,v)和I(0,-v)分别表示动子运动速度大小相同、方向相反而其他条件不变时线圈中电流。因此,本文设计的非线性阻力前馈补偿器uf表示为
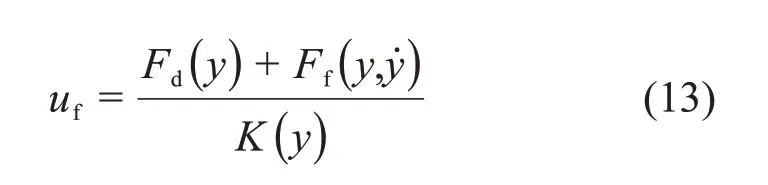
3 实验结果与讨论
为了验证平台结构和控制系统的性能,利用Matlab/Simulink软件包对二维平面运动平台进行实验测试。实验采用dsPACE数字控制原型系统[17],该系统的控制板为DS1005,还包括ADC,DAC和编码器接口电路;采用雷尼绍XL-80激光干涉系统作为第三方检测工具,其检测精度为1 nm。
3.1 重复性定位实验
为了验证平台运动到同一位置的可重复性,对平台进行重复定位精度测试。在平台新行程范围内,从零点以1mm为间隔取19个目标点,每个目标点采集8组数据,以同一目标点采集的数据平均值为参考位移,分析动平台在各目标位置的重复定位精度。图5所示为从X轴运动到各个目标点时的相对位置误差,可以发现沿X轴全行程运动时,重复定位误差为±0.20μm。图6所示为沿Y轴运动到各个目标点时的相对位置误差,可以发现沿Y轴全行程运动时,重复定位误差为±0.25μm。可以得出平台单轴运动时重复定位精度在±0.25μm以内。
3.2 三角响应
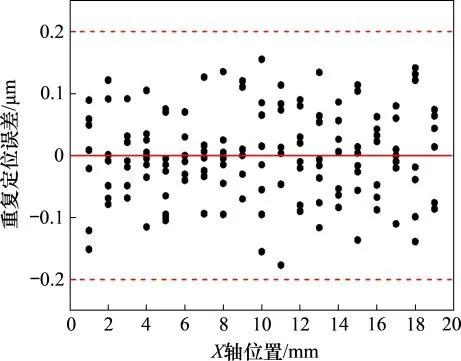
图5 X轴重复定位精度Fig.5 Repeated positioning accuracy of X axis
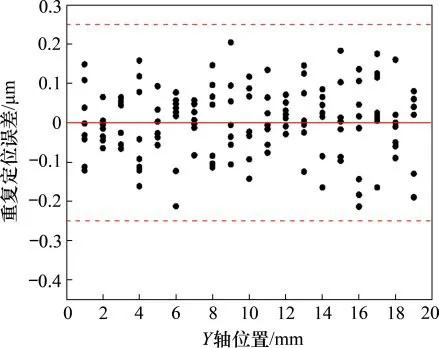
图6 Y轴重复定位精度Fig.6 Repeated positioning accuracy Y axis
为了说明定位阶段平台的跟踪能力,对平台三角形响应进行测试。动平台沿着Y轴移动100μm,图7所示为未加前馈控制的轨迹图,图8控制器对应的跟随误差曲线。从图7和图8可以看出:未加前馈控制器时,平台的跟踪误差在±1.00μm之内,但当平台突然改变运动方向时,其跟随误差突增到±5.00μm之内。从图9和图10可以看出:平台运动方向未改变时,其跟随误差为±0.20μm;当运动方向发生变换时,系统跟随误差为±0.60μm。与未加非线性阻力前馈补偿的PI控制器相比,当其跟踪误差特别是在平台运动方向发生突变时,加上前馈补偿后其跟踪性能明显提升。
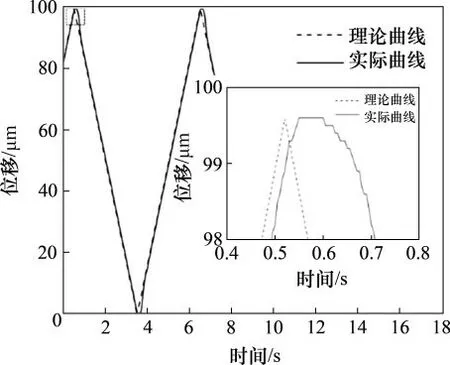
图7 PI控制器三角响应曲线Fig.7 Triangle response curve of PIcontroller
3.3 轨迹圆
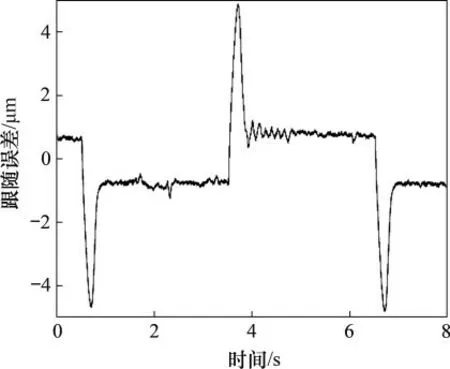
图8 PI控制器三角响应跟随误差曲线Fig.8 Triangular response followserror curve of PI controller
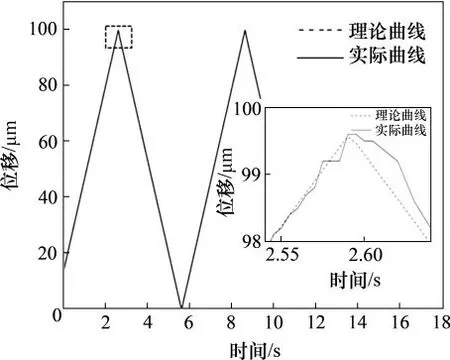
图9 PI+前馈补偿控制器三角形响应曲线Fig.9 Triangle response curve of PI and feedforward compensation controller
由于该平台是将X和Y运动限制在同一平面内,轨迹圆可以检验运动解耦方式的可行性和平所示为未加前馈控制的跟随误差曲线,图9所示为加上前馈控制器的轨迹图,图10所示为加上前馈台的联动性能,控制X和Y轴方向的电机同时运动,在同一平面内画1个以半径100μm轨迹圆,如图11所示。从图11可见:两轴联动时平台跟随误差为±2.00μm;理论轨迹圆和实际轨迹圆存在沿1个固定方向的偏移,其原因可能是用于运动解耦的直线轴承未能正交布置。
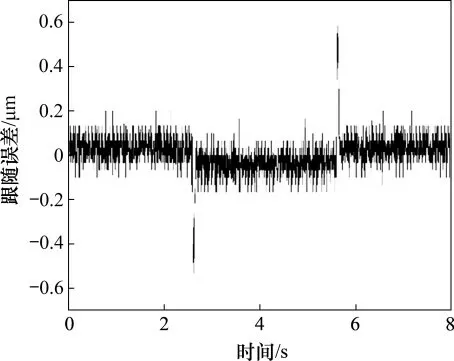
图10 PI+前馈补偿控制器跟随误差曲线Fig.10 Error curve of PI and feedforward compensation controller
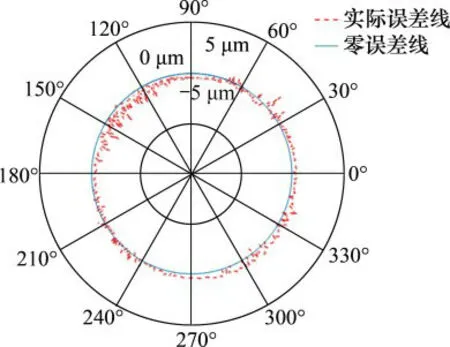
图11 轨迹圆Fig.11 Trajectory round
4 结论
1)使用直线电机直接驱动动平台来减少运动传递部件,利用直线轴承刚性解耦方式来减小控制系统复杂程度,同时结合高分辨率的直线光栅尺,动平台可以实现亚微米级二维平面运动平台设计。
2)采用传统PI控制器,平台在运动方向发生改变时,平台不能很好地进行变向跟随。基于直线电机工作原理,设计具有非线性阻尼前馈补偿的PI控制器,平台的跟随精度显著提升且平台的响应速度提高。
