舰载火箭炮高低机受力分析及传动误差研究

范虎成，方 帆，牛天宏，崔二巍，朱汉顺，柯 彪

(1.西北机电工程研究所，陕西 咸阳 712099；2.中国人民解放军32382部队，北京 100072)

舰载火箭炮高低机是按照射击诸元要求，赋予火箭炮起落架一定高低角的机构。其使用环境与陆装火箭炮有较大差别，舰船在水面航行时，受到风浪作用，船体时刻处于摇摆状态。为克服舰船摇摆运动对火箭炮发射的影响，火箭炮瞄准过程中需进行火力线稳定，以便在摇摆不定的舰船上使目标位置与火箭炮定向器指向保持相对稳定。在此过程中高低机承受力矩大、工况恶劣，不仅要克服火箭炮自身负载所产生的阻力，同时还需克服由于舰船摇摆导致火箭炮起落部分所产生的惯性力[1-2]。研究其受力状况可为火箭炮高低机结构设计、齿轮副寿命计算和使用安全性评估提供理论依据。火箭炮在瞄准过程中的火力线稳定精度，不仅与随动系统的伺服控制有关，高低机的传动精度对其也影响较大。研究高低机的传动误差可为随动系统伺服控制设计提供依据，对火箭炮的总体设计具有重要意义。

1 舰载火箭炮高低机受力分析

舰载火箭炮在瞄准过程中，高低机的阻力矩来源主要为起落部分自身负载力矩和舰船摇摆所引起的火箭炮起落部分的惯性力矩。起落部分负载力矩主要包括起落部分的重力矩、起落部分转动的摩擦力矩、瞄准过程的加速力矩和射击过程的冲击力矩。

1.1 起落部分自身负载力矩

起落部分的重力矩为

M1=mg·L0·cosβ，

(1)

式中：m为火箭炮起落部分的质量；L0为火箭炮耳轴中心与起落部分质心距离；β为火箭炮射角。

起落部分转动的摩擦力矩为

M2=Fe·f·d/2，

(2)

式中：Fe为火箭炮耳轴的支反力；f为火箭炮耳轴轴承的滚动摩擦系数；d为火箭炮耳轴轴承滚道直径。

瞄准过程的加速力矩为

M3=Jε，

(3)

式中：J为火箭炮起落部分的转动惯量；ε为火箭炮高低调炮加速度。

射击过程的冲击力矩为

M4=Q·L，

(4)

式中：Q为火箭炮射击过程中火箭弹的燃气流作用至发射架前端面的冲击力；L为耳轴中心点至燃气流冲击力作用线的垂直距离。

1.2 舰船摇摆的惯性力矩

目前，国际上对舰船甲板上放置货物的惯性力计算方法主要有IMO惯性力计算方法和基于简谐运动的惯性力计算方法。IMO惯性力计算方法主要考虑货物在舰船上的纵向和垂向位置，并没有指明货物重心距离水线的实际距离。基于简谐运动的惯性力计算方法在明确舰船最大横摇角、最大纵摇角和垂荡最大值后即可计算出惯性力最大值[3]。

舰船作为一个刚体在静水或波浪中受到扰动时，可能产生围绕其原始平衡做6个自由度的摇荡运动。由于实际海浪情况复杂多变，其运动往往是几种简单运动的叠加，相互间存在耦合影响。另外，由于舰船运动将对周围的流体产生扰动，改变了船体周围流体的速度场和压力场。波浪经过船体时，由于波浪起伏改变了船水下形状和体积，使浮力大小及作用点发生变化，因波浪下水质点作轨圆运动，将使波浪下的压力分布与静水面下的压力分布不同[1]。因此，从数学角度建立一个作用于船上完整而精确的力学模型是相对困难的。故通常在研究舰船摇荡时，作如下假设：

1)舰船在波浪中所作的6个自由度摇荡运动是相互独立的。

2)波浪是微幅平面进行波。

3)舰船摇荡幅值是微幅的。

在舰船可能产生的6个自由度的摇荡运动中，横摇、纵摇和升沉对火箭炮高低瞄准过程影响较大，其他3个自由度的摇荡可忽略不计。而横摇、纵摇和升沉均是以恢复力或恢复力矩作用，产生以平衡位置为中心的周期摇荡运动，它们均属于纯摇荡性的运动。横摇、纵摇和升沉的纯摇荡性运动非常接近简谐振荡。以横摇为例，运动过程中火箭炮所受的惯性力如图1所示。

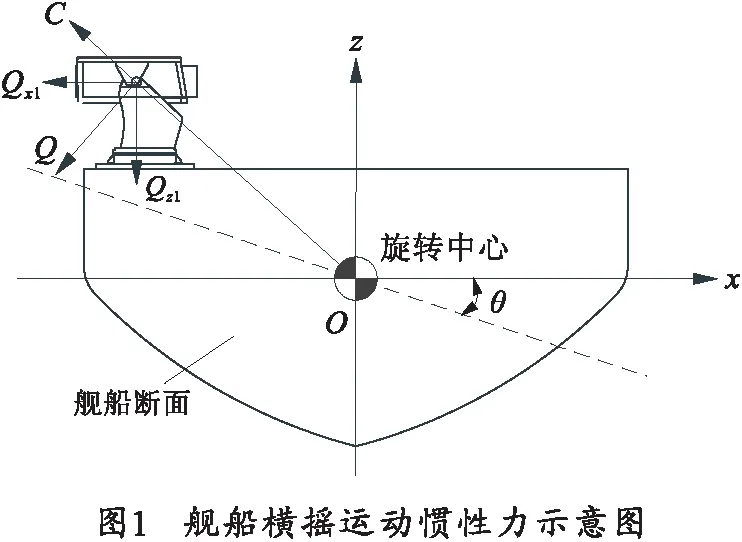
该横摇运动在火箭炮起落部分质心处产生切向力和法向力分别为：

Q=mRφAωφ2sinωφt，

(5)

C=mR(φAωφcosωφt)2，

(6)

式中：R为横摇运动旋转半径；φA为横摇的最大幅值；ωφ为横摇频率。

可见当横摇角度最大时，火箭炮起落部分受到的切向力最大，法向力为0，此时为火箭炮高低调炮受力最恶劣的状况。将切向力Q分解垂直于甲板方向Qz1和平行于甲板Qx1，其中Qz1为

Qz1=mφAωφ2X0，

(7)

式中，X0为火箭炮起落部分质心至舰船旋转中心的横向距离。

同理，纵摇所导致的切向力分解至垂直于甲板方向的最大分力为

Qz2=mθAωθ2Y0，

(8)

式中：θA为舰船纵摇的最大幅值；ωθ为纵摇的圆频率，ωθ=2π/T0；Y0为火箭炮起落部分质心至舰船旋转中心的纵向距离。

垂荡运动导致的火箭炮起落部分垂直于甲板方向的最大惯性力为

Qz3=mZHωH2，

(9)

式中：ZH为舰船垂荡的最大幅值，通常取浪高的1/2；ωH为垂荡频率，ωH=2π/TH.

由前述假设，舰船的各个自由度摇荡运动相互独立，将恶劣工况叠加，假定横摇、纵摇、垂荡最大值同时出现[3-4]，则火箭炮起落部分垂直方向受到的最大惯性力为

QZmax=m(ZHωH2cosφAcosθA+φAωφ2X0+θAωθ2Y0).

(10)

火箭炮起落部分的惯性力矩为

M5=m(ZHωH2cosφAcosθA+φAωφ2X0+θAωθ2Y0)L0.

(11)

综上所述，火箭炮高低机在稳瞄过程中受到的阻力矩为

(12)

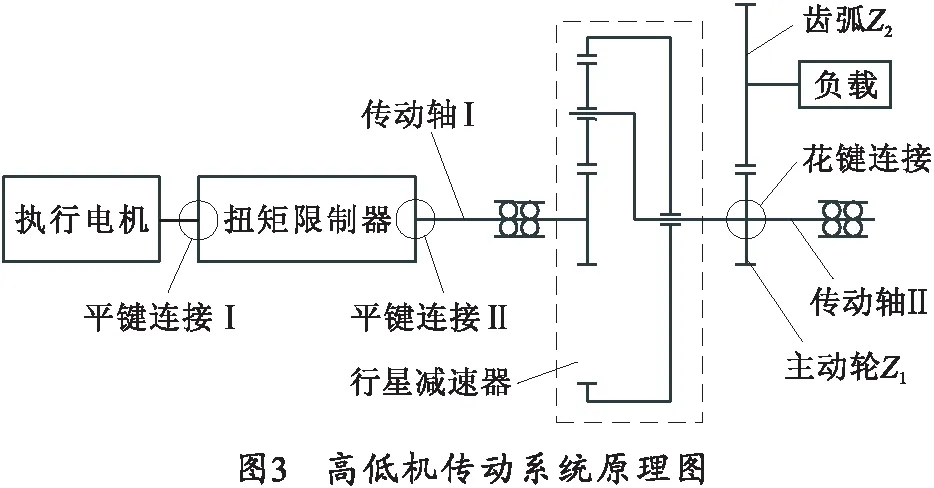
2 高低机传动误差分析

齿弧式高低机工作原理为电机通过联轴器带动减速器转动，减速器末端的主齿轮驱动齿弧实现火箭炮起落部分的运动。在高低机工作过程中，主齿轮转角的实际值与理论转角的差值，即为传动误差。按照误差形成的机理可将传动误差分为静态传动误差和动态传动误差[5]，静态传动误差主要由齿轮本身的侧隙、传动链各部件装配侧隙等造成；动态误差则是在传动扭矩的过程中由于传动轴、传动齿轮等传动部件受到负载扭矩而产生的扭转变形和弯曲变形导致的。目前国内对齿轮传动误差的计算方法主要有绝对值法、概率法、蒙特卡洛法。文献[6]和[7]中利用蒙特卡洛法进行误差计算，计算过程较繁琐，计算量很大，且对静态误差考虑不全面；文献[8]中利用概率法计算时并未考虑齿轮装配时轴承和键槽安装的误差。

2.1 静态传动误差分析

2.1.1 齿轮制造误差

齿轮加工制造时不同的精度等级有不同的公差，产生不同的齿轮侧隙。为便于测量，用公法线平均长度偏差来衡量齿厚偏差：

(13)

k1=|Es1|+|Es2|，

(14)

式中：Ews、Ewi分别为公法线平均长度上偏差和下偏差；Es1、Es2分别为两个齿轮的齿厚偏差；α为齿轮压力角。

齿轮在加工过程中，要先将毛坯进行定位，再进行加工。但实际中由于毛坯定位时会出现圆的理论中心与实际中心的偏差，齿轮啮合过程中，中心距会产生一定的变化，引起圆周侧隙：

k2=2egsinφtanα，

(15)

故齿轮副传动时齿轮制造误差角为

(16)

式中，d2为从动轮的分度圆直径。

2.1.2 装配的空回误差

高低机在传动过程中除了齿轮啮合，还有轴承、传动轴与键连接等多个环节，其中齿轮中心距偏差、轴承的间隙、键与键槽的间隙均可导致传动过程的圆周侧隙[10]。

齿轮中心距偏差发生在齿轮齿宽的中间平面内，影响齿轮的径向侧隙。根据齿轮径向侧隙与圆周侧隙关系可得出：

j1=2fatanα，

(17)

式中，fa为齿轮中心距偏差。

轴承本身在制造过程中的误差和装配时内外圈配合间隙均可能导致传动过程的圆周侧隙：

(18)

式中：Δr为轴承径向游隙；Δbi为轴承内环与轴配合间隙；Δbo为轴承外环与箱孔的配合间隙。

键与键槽的间隙导致的圆周侧隙[6]为

j3=KkΔCk，

(19)

式中：Kk为键槽间隙对侧隙的影响系数；ΔCk为键与轮毂键槽之间的间隙。

装配的空回误差为

(20)

由于静态传动误差的随机性，根据数理统计知识，各项误差相互独立且服从正态分布，根据概率法计算可知：

(21)

由式(21)，可计算出静态传动误差：

ε=3σ,

(22)

则高低机整个传动系统的静态传动误差是各级传动副的叠加，且具有随机性，故

(23)

式中，i2，i3，…，ik为各级齿轮副传动比。

2.2 动态传动误差分析

2.2.1 传动轴的扭转变形导致的回转误差

利用材料力学的相关知识可知，传动轴的扭转变形角为

(24)

式中：T为传动轴上的扭矩；Ct为扭转刚度。

高低机由轴扭转变形产生的传动误差为

(25)

2.2.2 传动轴的弯曲变形导致的回转误差

为了便于研究，通常将轴简化为简支梁，在啮合线方向的挠度为

(26)

式中：Fn为法向啮合力；L，a，b为跨距及受力点距支撑点距离；E为弹性模量；ds为轴径。

挠度f可分解为切向和径向分量，产生的圆周侧隙为

(27)

故轴的弯曲变形导致的回转误差角为

(28)

2.2.3 传动齿轮的扭转变形导致的回转误差

传动齿轮在传动轴扭矩作用下产生一定的扭转变形。根据扭转啮合刚度理论，扭转变形主要包括轮毂扭转变形、齿根弯曲变形和齿面接触变形，齿轮承受的扭矩载荷与该载体的弹性扭转角的比值即为该齿轮的扭转啮合刚度。因齿轮啮合时的扭转变形涉及因素较多，用理论方法计算该变形较为困难，利用Ansys workbench工具，对啮合齿轮进行有限元分析，计算齿轮在扭矩T作用下的扭转变形角位移。齿轮的约束与加载情况如图2所示。

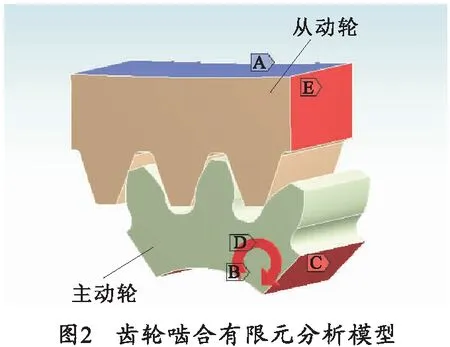
从动轮内圆柱面施加固定约束A，模型的切断面施加Displacement约束E；主动轮内柱面添加周转约束B，内柱面施加扭矩载荷D，模型的切断面施加Displacement约束C.依据Ansys workbench的仿真分析云图，利用插值法得到分度圆处的扭转变形角位移：

(29)

考虑齿轮传动过程单双齿交替啮合，变形持续变化，齿轮分度圆处的扭转变形角为

(30)

式中，εa为齿轮重合度，高低机传动系统导致齿轮的扭转变形导致的回程误差为

(31)

可知传动系统的动态误差为

ε∑2=φ∑+λ+χ∑.

(32)

综上，舰载火箭炮高低机在传动总误差为

ε∑=ε∑1+ε∑2.

(33)

3 实例分析

以某舰载型火箭炮为例，采用上述方法计算该高低机的受力及传动误差。

火箭炮基本参数如表1所示，舰船摇摆及火箭炮安装参数如表2所示。主齿轮与齿弧及传动轴材料均为42CrMo，弹性模量为E=212 GPa，泊松比为0.28，剪切模量G=79 GPa.

表1 火箭炮基本参数

表2 舰船摇摆及火箭炮安装参数

3.1 舰载火箭炮高低机受力计算

根据表1和2的数据，由式(1)～(12)计算可得该舰载火箭炮高低机在加速调炮过程中，最大负载力矩如表3所示。

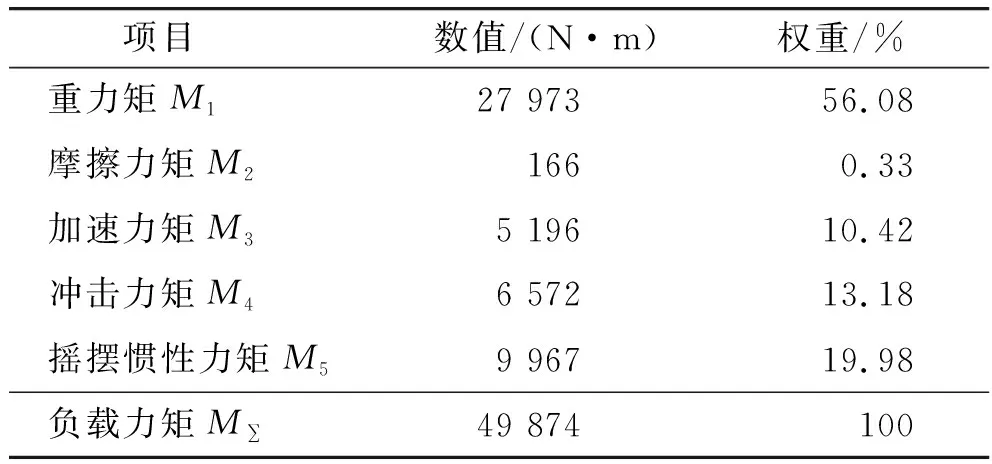
表3 高低机调炮过程负载力矩

由表3可知，高低机调炮过程中，重力矩和摇摆惯性力矩为负载力矩的主要构成部分，由计算公式可知，若减小耳轴中心与起落部分质心距离，则可有效地降低重力矩和摇摆惯性力矩；同时舰船自身的摇摆参数和火箭炮在舰船的安装位置对摇摆惯性力矩影响较大，在同样的安装位置下，若选择较大排水量舰船，则摇摆幅值减弱、周期延长，摇摆惯性力矩降低；对于同一艘舰船，安装位置越靠近舰船摇心则摇摆惯性力矩越低。

3.2 高低机传动误差计算

某舰载火箭炮高低机传动原理如图3所示。因扭矩限制器与行星减速器均为成熟产品，故在计算过程中将其作为整体部件进行分析计算。扭矩限制器扭转刚度Ct1=122 N·m/(′)；行星减速器速比i=35，扭转刚度Ct2=1 400 N·m/(′)，回程间隙jt=3′.

3.2.1 高低机静态传动误差计算

高低机基本参数如表4～6所示。

表4 齿轮副基本参数

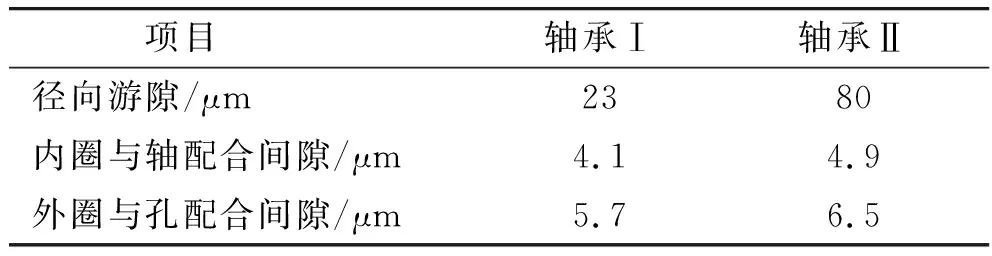
表5 轴承基本参数

表6 平键与花键基本参数

根据表4～6数据，计算高低机静态传动误差，可将主齿轮与齿弧传动副前的传动环节折合至该传动副进行计算，由公式(13)～(23)计算可知，高低机传动系统的齿轮制造误差φ=1.09′，装配空回误差为γ=0.77′，总静态误差为ε∑1=0.67′.

3.2.2 高低机动态传动误差计算

3.2.2.1 传动轴的扭转变形回转误差计算

根据高低机传动原理，在传动过程中，传动轴Ⅰ和Ⅱ、扭矩限制器、行星减速器均可按照传动轴计算扭转变形，由表3高低机调炮过程负载力矩可知各传动部件受到的扭矩，如表7所示。

表7 各传动部件的扭矩

由公式(24)、(25)计算高低机传动部件扭转变形导致的回程误差φ∑=1.61′.

3.2.2.2 传动轴弯曲变形导致的回转误差计算

由高低机结构分析可知，在传动过程中，传动轴Ⅱ在齿轮副法向啮合力作用下，产生弯曲变形。根据负载力矩，法向啮合力Fn=51 428 N，传动轴Ⅱ总长L为210 mm，受力点距两端支撑点距离a、b分别为93、117 mm，轴径ds=69 mm.由式(26)可计算得啮合点的挠度f=2.05，产生的圆周侧隙eg=4.36，回转误差角λ=0.015′，故高低机传动系统由轴弯曲变形产生的传动误差为：λ∑=0.015′.

3.2.2.3 传动齿轮扭转变形导致的回转误差计算

根据高低机齿轮副所承受的负载扭矩，利用Ansys workbench有限元仿真工具，计算传动齿轮的扭转变形导致的回转误差。将三维模型导入Ansys workbench中，设置齿轮材料力学性能参数，划分Hex Dominant类型网格，设置齿轮啮合面，将齿弧内柱面固定，主动轮内柱面施加扭矩，仿真分析结果如图4所示。

根据齿轮副仿真应变云图，分别在Ansys workbench后处理器中测量出主动轮Z1、齿弧Z2的齿顶圆位移xa和齿根圆位移xf，由式(29)计算出分度圆处的扭转变形位移，由式(30)计算分度圆处的扭转变形角，结果如表8所示。

表8 齿轮的扭转变形角计算

由式(31)计算可得齿轮副扭转变形导致的回转误差χ∑=0.919′.由式(32)、(33)可知，当起落部分运动加速度为25(°)/s2时，高低机动态传动误差为χ∑2=2.544′，传动总误差为χ∑=3.214′，与一般火炮瞄准机8′～10′传动误差相比，该高低机传动误差较小，主要原因在于该高低机传动过程简单、动力传递环节较传统瞄准机构少；传动链整体刚度好，使用高精度行星减速器，降低传动过程的误差，提高了舰载火箭炮的稳瞄精度。

经对试制完成的该舰载火箭炮高低机传动系统误差测量，传动总误差约为3.43′，进一步验证了传动误差分析过程及计算公式的正确性。

4 结束语

根据舰载火箭炮瞄准过程高低机的受力情况，详细分析了高低机负载力矩组成并推导了各组成部分及总负载力矩的计算公式；采用概率法对高低机的静态传动误差进行了分析，基于高低机运动过程所承受的负载力矩，利用有限元计算工具对齿轮传动过程进行仿真分析，得到高低机的动态传动误差，最后得出舰载火箭炮高低机瞄准过程总传动误差。结合实例计算结果，分析了高低机负载力矩各组成部分的权重及影响因素，对比分析了传动总误差与一般火炮传动误差值，验证了计算公式的正确性，研究结果可为舰载火箭炮总体设计和研究高低机对稳瞄精度的影响提供参考。