基于数字图像的试样表面应力估算及应用
2020-06-16张磊李树刚申凯潘红宇张天军
张磊 李树刚 申凯 潘红宇 张天军


摘 要:為获得试样破坏过程中的表面应力分布特征,提出了基于数字图像的试样表面应力估算方法。开展了含孔试样破坏的应力场演化观测试验,利用数字图像相关技术获得试样破坏过程中的图像序列,采用VIC-3D软件计算试样的表面变形场及应变场。结合所得应变场数据及应力估算方法,计算得到试样表面应力。采用虚拟场理论建立了表面应力与轴向应力的关系,且据此评估了3种弹性模量及5种泊松比的估算效果,优选了最佳应力估算参数组合。最后将应力估算方法应用于试样破坏过程中的应力场演化分析,对比验证了应力估算准确性。结果表明:弹性模量仅影响应力估算的峰值大小,不改变应力的分布,由数字图像计算得到的平均泊松比μ3在估算时稳定性较好;采用平均弹性模量Eav以及平均泊松比μ3估算加载中期的应力较为准确;估算所得表面应力能够完整的反应试样破坏过程,表面应力集中与裂纹萌生存在对应关系。数字图像相关方法的应力估算能够量化表面应力,研究可为实验力学中的表面应力分析提供参考。
关键词:应力估算;数字图像相关;表面应力;参数优选;应力演化
中图分类号:O 348.1
文献标志码:A
文章编号:1672-9315(2020)02-0229-09
DOI:10.13800/j.cnki.xakjdxxb.2020.0206开放科学(资源服务)标识码(OSID):
Estimation and applicationof sample surface
stressbased on digital image
ZHANG Lei1,LI Shu-gang2,SHEN Kai3,PAN Hong-yu2,ZHANG Tian-jun2,4
(1.College of EnergyEngineering,Xian University of Science and Technology,Xian 710054,China;
2.College of Safety Science and Engineering,Xian University of Science and Technology,Xian 710054,China;
3.China Coal Technology and Engineering Group Chongqing Research Institute,Chongqing 400037,China;
4.College ofSciences,Xian University of Science and Technology,Xian 710054,China)
Abstract:In order to explore the surface stress distribution characteristics during the failure process of the specimen,a stress estimation method based on digital image correlationwas proposed.An experiment of observing the stress field evolution of the hole-containing samples was carried out.The image sequence in the destruction process of the sample was obtained by digital image correlation technology.The surface deformation field and strain field of the sample were calculated by VIC-3D.Based on the obtained strain field data and the stress estimation method,the surface stress of the sample was calculated.The relationship between the surface stress and the axial stress was established by using the virtual field theory,and the estimation effects of 3 kinds of elastic modulus and 5 kinds of Poissons ratio were evaluated,and the optimal stress estimation parameter combination was optimized.The stress estimation method was applied to the stress field evolution analysis during the sample failure process,thus verifying the accuracy of the stress estimation.The results show that the elastic modulus only affects the peak value of the stress estimation,without changing the stress distribution.The average Poissons ratio obtained by DIC has better stability in the estimation.It is more accurate to estimate the stress in the middle of loading by the average elastic modulus Eav and the average Poissons ratio μ3.The obtained surface stress by estimating can completely reveal the destroy degree of the sample,and the surface stress concentration corresponds to the crack initiation.The stress estimation of the digital image correlation method can quantify the surface stress,and the research can provide a reference for the surface stress analysis in experimental mechanics.
Key words:stress estimation;digital image correlation;surface stress;parameter optimization;stress evolution
0 引 言
数字图像相关方法(Digital image correlation,简称DIC)是一种基于数字图像的非接触式测量方法,能够获取试样表面的变形信息。DIC通过计算对比图像变形前后的移动情况,从而获得试样表面位移矢量[1]。
最早使用DIC研究试样变形的报道出现于1982年[2],文中提出了通过子网格匹配图像的方法,用于确定试样位移,奠定了DIC计算位移的理论基础。接着,Sutton据此完善了数值计算的流程,并编制了著名的2D-DIC软件,形成了快速计算位移的方法[3]。但是,并不是所有的位移都可以用整像素来表达。子网格匹配算法仅能识别出整像素的位移,从而导致测量结果存在误差。为解决试件移动非整像素的问题,潘兵在位移计算中引入曲面拟合,提出了亚像素位移测量方法[4-5]。至此,DIC形成了完备的测量技术,出现了成熟的计算分析软件。例如,美国Correlated Solutions公司的商用计算软件VIC-3D[6],美国桑迪亚国家技术和工程中心的开源软件DICe[7],美国乔治亚理工的开源分析软件Ncorr[8],西安交通大学自研的应变分析系统XJTUDIC[9],罗马大学的开源软件py2DIC[10]以及法国巴黎高等师范学院的图像分析软件CORRELIQ4[11]。
随着DIC软件的成熟,研究人员借助这些软件开展了大量研究。Pierron总结了这些研究,认为研究的主要因素包括几何结构、外荷载、外支撑、本构方程、本构参数、位移、应变及应力[12]。根据这些因素已知或未知的状态,可将研究分为变形观测、特征参数求取以及应力与荷载重构3个方面。在变形观测方面,马少鹏利用DIC研究了岩石破坏过程中裂纹扩展的应变局部化问题[13]。基于应变局部化分析,包林海进一步讨论了应变局部化中的变异系数演化规律[14]。张天军则提取DIC的原始数据,研究钻孔孔壁的移动规律[15-17]。潘红宇
分析DIC的原始数据,深入研究裂尖应变率特征[18-19]。在参数测定方面,
Grédiac,Avril等
基于虚拟场原理,给出了基于DIC技术计算材料弹性模量及泊松比的方法[20-21]。代树红给出了利用DIC技术测定了Ⅰ-Ⅱ型裂纹应力强度因子的方法[22-23]。在应力与荷载重构方面,AVRIL在本构参数的研究中,利用虚拟场理论估算试样应力,并用荷载重构的方法来验证估算的有效性[24]。
Krfmann基于Love-Kirchhoff假定,选取了不同重构窗函数,估算了喷嘴附近薄板压力,初步实现了异形材料的荷载重构[25]。
不難发现,使用DIC的研究人员不仅希望得到试样变形与应变,而且还期望得到试样表面的应力分布及未知荷载等参数。但是,DIC测量的直接信息较为匮乏,有待进一步处理运算。应力作为反映试样受力状态的重要物理量,不仅可以表征试样的破坏状态,而且还是荷载重构必不可少的关键物理量。为此文中针对基于DIC的应力估算方法开展研究,运用理论分析与试验观测的方法,优选应力估算参数,提出基于数字图像的试样表面应力估算方法,并将该方法应用于含孔试样破坏的应力场演化研究。
1DIC及应力估算模型
1.1 相关性计算
在DIC计算中,运算的核心是匹配变形前后的图像。首先,选取变形前后的2幅图像进行匹配。在遍历图中所有区域的过程中,计算两图的相关性系数C.当相关性系数C取得最小值时两图的相似程度最大。典型的相关性系数计算方法如式(1)所示
式中 x为灰度值;f(x)为参考图像的像素灰度分布;g(x)为变形后图像的像素灰度分布;R为分析区域。
接着,通过比对变形前后图像的位置,获取点对点的位移,如图1所示。
1.2 应变计算
获得了位移场后,通过拟和及差分运算计算应变场。首先,在待测点选取一个较小的连续区域,获得这个区域的位移数据。接着,采用最小二乘法得到拟和平面,并建立以该测点为中心的局部坐标系。试样表面每一个测点的所有位移分量被转换到局部坐标系下,对不同位移分量差分形成ε11,ε22以及ε12等应变分量。典型的差分公式如式(2)
式中 ε11,ε22及ε33分别为三向主应变矩阵;ε12,ε23及ε31分别为三向切应变矩阵;d1 d2 d3分别为三向位移,X1 X2 X3为三向坐标。
1.3 应力估算的本构方程
得到试样的应变后,可根据试样的本构方程来估算试样的应力。采用弹性本构时,应力可由应变、弹性模量E及泊松比μ计算得到,方程如下
式中 σ为应力张量;ε为应变张量;Q为弹性本构参数;E为弹性模量;μ为泊松比。
试验中,弹性模量E可由应力应变曲线测算获得;泊松比μ可由应变计算得到,应力估算的主要流程如图2所示。
2 估算参数选取及评价方法
2.1 试样制备及试验方法
试样为石膏立方块体,设计孔径为10 mm,为避免孔周应力集中对试验的影响,孔壁距离试样端面为3倍孔径,试样边长为70 mm.配制试样浆液时,石膏及水以质量比7
∶3混合,将水倒入石膏粉末中并快速搅拌,防止石膏凝固。经过2 min充分搅拌后,将所得浆液浇注于70 mm×70 mm×70 mm方形试样盒中。随后于试样盒中置入直径为10 mm,高为100 mm圆柱体,以此预制孔洞,所制试样情况见表1.
加载中期,采用μ1,μ2,μ3及μ5估算得到应力均能较好的反应出应力随应变增大而增长的趋势。而采用μ4计算得到的应力,离散程度过高,无法用于表征该阶段内的应力应变规律。
加载末期,采用μ2及μ5估算得到的应力能够反应出试样破坏后应力降低的情况。而采用μ1,μ3及μ4估算得到的应力依旧呈现出急剧上升的趋势。这是由于试样破坏后,仅局部区域呈现出压缩状态,而破坏区域应力释放,将导致横向应变减小。从整个试样的变形状态来看,体积应变在破坏后迅速降低[29]。轴向应变不变的情况下,横向应变将显著降低,泊松比将显著减小,故μ2及μ5这种小泊松比更贴近实际情况,用其估算得到的应力趋势与试验机所测趋势表现一致。但由于弹性阶段内的横向应变过小,弹性体积应变小于实际发生值,估算应力的峰值显著低于所测值。
泊松比反应了试样的整体变形情况,从体积应变的角度影响试样的应力估计。在加载初期和加载末期,小泊松比更能反映实际趋势;而在加载中期,大泊松比更靠近试样实际变形,从而应力估算更为准确一些。
3.3 应力估算的误差
利用所述方法估算此次3个试样的应力,统计估算应力应变曲线与试验机实测曲线的均方根误差,见表4.
表中均方根误差越小意味着应力估算结果越贴近试验机实测值。统计表明,
Eav-μ3为最优应力估算组合,在所有试样的应力估算中误差最小。
4 含孔试样的表面应力估算
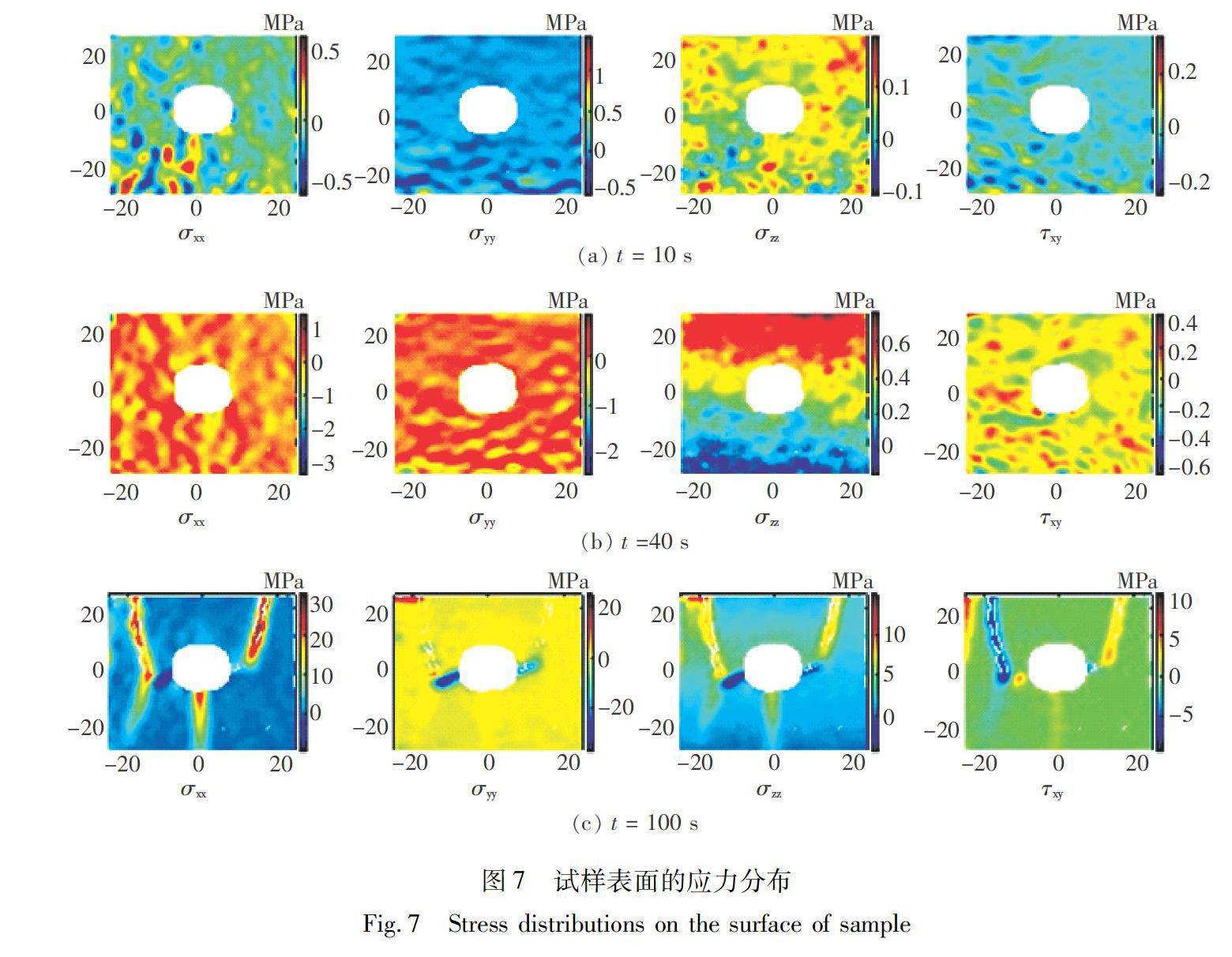
采用Eav-μ3应力估算参数组合,进行试样表面应力反演,开展含孔试样破坏过程中表面应力场演化研究,得到含孔试样在不同破坏阶段的应力分布云图,如图7所示。
图7为B3试样在初始阶段、弹性阶段以及裂纹萌生阶段应力估算分布。与试样的破坏阶段相对应,应力也呈现出3个阶段,这与文献[17]中应
力分布规律呈现出由混乱到有序的表述是相符的。
图7(c)中孔底的裂纹呈现出σxx应力显著集中,该区域发生了水平方向的拉伸破坏。这种破坏形式与文献[16,30]中孔底产生拉伸破坏的结论一致。而试样由上端面向下延伸出的裂纹也呈现出σxx应力集中,说明这个区域存在拉伸破坏,这与文献[30]第2拉伸裂纹出现的描述对应。图7(c)中孔侧裂纹呈现出σyy应力显著下降,这是由于在该处产生了压缩错动,形成了小范围的屈服。来自于试样顶端的荷载在孔侧不能完全传递到至试样底端,造成了此处σyy应力低于试样其他区域。这样的破坏形式同样在文献[30]中有明确的描述。
可以发现,估算的表面应力能够反应试样破坏过程中的应力集中,且与裂隙扩展演化存在对应关系,能够为表面应力分析提供参考。
5 结 论
1)在采用弹性本构时,弹性模量对应力估算有显著的影响。弹性模量影响应力估算的峰值大小,不改变应力的分布。试样表面应力的峰值大小随弹性模量增大而增大;应力应变曲线随弹性模量增大而升高。
2)泊松比在不同阶段对应力估算的影响表现不同。在加载初期和加载末期,经典泊松比μ5及混合平均泊松比μ2更能反映实际趋势;而在加载中期,DIC平均泊松比μ3更靠近试样实际变形,估算应力更接近实测值。
3)采用平均弹性模量Eav以及由DIC平均泊松比μ3可以较为准确地估算加载中期试样的表面应力。
参考文献(References):
[1] 潘 兵,吴大方,夏 勇.数字图像相关方法中散斑图的质量评价研究[J].实验力学,2010,25(2):120-129.
PAN Bing,WU Da-fang,XIA Yong.Study of speckle pattern quality assessment used in digital image correlation[J].Journal of Experimental Mechanics,2010,25(2):120-129.
[2]Peters W H,Ranson W F.Digital imaging techniques in experiment stress analysis[J].Optical Engineering,1982,21(3):427-431.
[3]
Sutton M,Wolters W J,Peters W,et al.Determination of displacements using an improved digital correlation method[J].Image and Vision Computing,1983,1(3):133-139.
[4]
潘 兵,續伯钦,陈 丁,等.数字图像相关中亚像素位移测量的曲面拟合法[J].计量学报,2005,26(2):128-134.
PAN Bing,XU BO-qin,CHEN Ding,et al.Sub-pixel registration using quadratic surface fitting in digital image correlation[J].Acta Metrologica Sinica,2005,26(2):128-134.
[5]潘 兵,谢惠民,续伯钦,等.数字图像相关中的亚像素位移定位算法进展[J].力学进展,2005,35(3):345-352.
PAN Bing,XIE Hui-min,XU Bo-qin,et al.Development of sub-pixel displacements registration algorithms in digital image correlation[J].Advances in Mechanics,2005,35(3):345-352.
[6]Van Mieghem B,Ivens J,Van Bael A.Consistency of strain fields and thickness distributions in thermoforming experiments through stereo DIC[J].Experimental Techniques,2016,40(5):1409-1420.
[7]Turner D Z.Digital Image Correlation engine(DICe)reference manual[EB/OL].http://dicengine.github.io/dice/,2018-09-26/2019-09-17
[8]
Blaber J,Adair B,Antoniou A.Ncorr:open-source 2D digital image correlation matlab software[J].Experimental Mechanics,2015,55(6):1105-1122.
[9]
梁 晋,郭 翔,胡 浩,等.机械与材料力学性能的三维全场变形与应变快速检测研究[J].中国工程科学,2013,15(1):51-56.
LIANG Jin,GUO Xiang,HU Hao,et al.Study on rapid 3D full-field deformation&strain measurement and inspection for mechanical engineering and material mechanical properities[J].Strategic Study of CAE,2013,15(1):51-56.
[10]
Ravanelli R,Nascetti A,Di Rita M,et al.A new digital image correlation software for displacements field measurement in structural applications[M].XLII-4/W2,2017.
[11]
Cachan E N S.CORRELIQ4:A software for “finite-element” displacement field measurements by digital image correlation[R].Cachan Cedex,France:LMT-Cachan,2019.
[12]
Pierron F,Grediac M.The virtual fields method[M].New York:Springer,2012.
[13]
马少鹏,金观昌,潘一山.白光DSCM方法用于岩石变形观测的研究[J].实验力学,2002,17(1):10-16.
MA Shao-peng,JIN Guan-chang,PAN Yi-shan.Study on the white light DSCM method for deformation measurement of rock materials[J].Journal of Experimental Mechanics,2002,17(1):10-16.
[14]包林海,马少鹏,王建新.含转折非连通断层岩石破坏过程的试验研究[J].土木工程与管理学报,2011,28(4):58-60.
BAO Lin-hai,MA Shao-peng,WANG Jian-xin.Experimental study on the failure process of a rock with tortuously non-connected fault[J].Journal of Civil Engineering and Management,2011,28(4):58-60.
[15]
張天军,张 磊,李树刚,等.瓦斯抽采钻孔孔周裂纹扩展规律[J].辽宁工程技术大学学报,2018,37(3):499-507.
ZHANG Tian-jun,ZHANG Lei,LI Shu-gang,et al.Crack propagation around gas drilling borehole[J].Journal of Liaoning Technical University(Natural Science),2018,37(3):499-507.
[16]张天军,张 磊,李树刚,等.含孔试样渐进性破坏的表面变形特征[J].煤炭学报,2017,42(10):2623-2630.
ZHANG Tian-jun,ZHANG Lei,LI Shu-gang,et al.Characteristics of the surface deformation of specimens with a hole during the progressive failure[J].Journal of China Coal Society,2017,42(10):2623-2630.
[17]
Zhang T,Zhang L,Li S,et al.Stress inversion of coal with a gas drilling borehole and the law of crack propagation[J].Energies,2017,10(11):1743.
[18]潘红宇,董晓刚,张天军,等.单轴压缩下松软煤样破裂损伤演化特性研究[J].西安科技大学学报,2018,38(2):202-209.
PAN Hong-yu,DONG Xiao-gang,ZHANG Tian-jun,et al.Evolution characteristics of soft coal sample fracture damage under uniaxial compression[J].Journal of Xian University of Science and Technology,2018,38(2):202-209.
[19]潘红宇,葛 迪,张天军,等.应变率对岩石裂隙扩展规律的影响[J].煤炭学报,2018,43(3):675-683.
PAN Hong-yu,GE Di,ZHANG Tian-jun,et al.Influence of strain rate on the rock fracture propagation law[J].Journal of China Coal Society,2018,43(3):675-683.
[20]Gr Diac M,Pierron F,Avril S,et al.The virtual fields method for extracting constitutive parameters from full-field measurements:a review[J].Strain,2006,42:233-253.
[21]Avril S,Pierron F.General framework for the identification of constitutive parameters from full-field measurements in linear elasticity[J].International Journal of Solids and Structures,2007,44:4978-5002.
[22]代树红,马胜利,潘一山.数字图像相关法测定岩石Ⅰ-Ⅱ复合型裂纹应力强度因子[J].岩土工程学报,2013,35(7):1362-1368.
DAI Shu-hong,MA Sheng-li,PAN Yi-shan.Evaluation of mixed-mode I-II stress intensity factors of rock utilizing digital image correlation method[J].Chinese Journal of Geotechnical Engineering,2013,35(7):1362-1368.
[23]代樹红,马胜利,潘一山,等.数字散斑相关方法测定岩石Ⅰ型应力强度因子[J].岩石力学与工程学报,2012,31(12):2501-2507.
DAI Shu-hong,
MA Sheng-li,PAN Yi-shan,et al.Determination of mode I stress intensity factors by digital speckle correlation method[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(12):2501-2507.
[24]Avril S,Pierron F,Sutton M A,et al.Identification of elasto-visco-plastic parameters and characterization of L ders behavior using digital image correlation and the virtual fields method[J].
Mechanics of Materials,2008,
40(9):729-742.
[25]
Kaufmann R,Ganapathisubramani B,Pierron F.Full-field surface pressure reconstruction using the virtual fields method[J].Experimental Mechanics,2019,59(8):1203-1221.
[26]
Fairhurst C E,Hudson J A.Draft ISRM suggested method for the complete stress-strain curve for intact rock in uniaxial compression[J].International Journal of Rock Mechanics and Mining Sciences & AMP,Geomechanics Abstracts,1999,36(3):279-289.
[27]
王学滨,杜亚志,潘一山,等.基于DIC粗-细搜索方法的单向压缩砂样的侧向变形观测研究[J].工程力学,2013,30(4):184-190.
WANG Xue-bin,DU Ya-zhi,PAN Yi-shan,et al.Lateral deformation measurements for sand specimens under uniaxial compression based on digital image correlation with coarse-fine search method[J].Engineering Mechanics,2013,30(4):184-190.
[28]
涂忠仁,杨 强.岩体负泊松比试验研究[J].岩土力学,2008,29(10):2833-2836.
TU Zhong-ren,YANG Qiang.Test research on negative Poissons ratio of rock mass[J].Rock and Soil Mechanics,2008,29(10):2833-2836.
[29]张晓平,王思敬,刘泉声.一种测量岩石压缩裂纹扩展过程声波波速的连续测量方法[J].工程地质学报,2018,26(1):91-96.
ZHANG Xiao-ping,WANG Si-jing,LIU Quan-sheng.A continuing measure method for acoustic wave velocity measurement during cracking processes of rock[J].Journal of Engineering Geology,2018,26(1):91-96.
[30]Lajtai E Z,Lajtai V N.The collapse of cavities[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1975,12(4):81-86.
