基于ACO-BP神经网络的土石坝位移监测模型研究
2020-06-16茹秋瑾何自立杨军超李晓琳谭剑波
茹秋瑾,何自立,杨军超,李晓琳,谭剑波,
(1.杨凌职业技术学院,陕西 杨凌 712100;2.西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100;3.陕西省引汉济渭工程建设有限公司,陕西 西安 710010)
1 研究背景
安全监测是大坝运行管理的一项重要工作,通过安全监测数据分析可以及时准确了解大坝运行状况。国内外大坝安全监测主要采用数学模型(统计模型、确定性模型和混合模型)来进行模拟分析和预测预报[1-2],如:神经网络、层次分析、模糊综合评价和熵权等模型预测,但单一模型很难兼顾模型参数指标的随机性和模糊性,预测分析数据结果准确性不高、可信性较差[3]。近年来,许多学者针对大坝安全预测模型、安全监测评价模型等进行优化改进,并取得较多研究成果。张柯等[4]采用ABC(artificial bee colony)人工蜂群算法对土石坝变形的SVM(support vector machine)支持向量机模型进行优化,使模型拟合度和预测精度得到提高,泛化能力加强。冯学慧[5]提出基于熵权法与正态云模型结合的大坝安全监测评价体系,通过隶属度来评价大坝安全等级。何金平等[6]在文献中提出基于云模型的大坝安全监测评价方法,来处理大坝安全监测中存在的信息不确定性风险。王娟等[7]采用KICA(kernel independent component analysis)核独立分量分析原始样本数据的非线性特性,并结合RVM(relevance vector machine)关联向量机对大坝缺失监测数据进行插值回归。本文基于翟旭瑞等[8]提出的BP神经网络模型,采用ACO(ant colony optimization)蚁群算法对多层网络隐含单元的连接权值和阈值进行优化,构建ACO-BP神经网络模型自动预测分析大坝变形位移,使土石坝安全监测预报更为方便和准确。
2 BP神经网络模型
2.1 BP网络结构
BP神经网络模型一般由输入层、隐含层和输出层3部分组成。文中采用3层BP网络结构,隐含层采用函数Tansig,输出层采用函数Purelin,通过网络自动学习耦合输入和输出样本数据间的任意非线性关系[9-10],BP神经网络结构如图1所示。
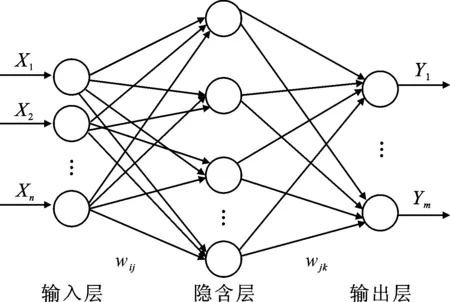
图1 BP神经网络结构图
2.2 土石坝位移影响因子
土石坝变形[11]是大坝监测中的重要监测项目,包括水平位移、竖向位移和纵向位移,其中以竖向位移(沉降量)为最大。竖向位移主要影响因素包括库水压力、温度效应和时效效应,即:
δ=f(δH)+f(δT)+f(δθ)
(1)
式中:δH为库水压力分量;δT为温度分量;δθ为时效分量。
大坝竖向位移和各变量间的映射关系为:
δ=F(δH,δT,δθ)
(2)
(1)水压分量δH。土石坝水压力主要由上游水体压力引起,压力可以分解为水平分量和竖直分量,而竖直位移主要由竖直分量引起,即:
(3)
式中:H为观测竖向位移时的坝前水深,即库水位减去坝底高程,m;H0为建模资料系列起始日的水深,m;ai为水压分量的影响系数。
(2)温度分量δT。已建大坝坝体内各点的温度主要与气温和水温的变化有关,主要采用气温作为分析因子。同时,考虑坝体内温度变化滞后于气温变化,即:
(4)
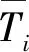
(3)时效分量δθ。在水压、大坝自重等荷载作用下,时效变量的影响最为显著,即:
δθ=c1θ+c2lnθ
(5)
式中:θ为监测日至建模系列起始日的累计天数除以100,d;c1、c2为时效分量的影响系数。
综合水压、温度和时效分量,建立土石坝竖向位移的关联性数学模型,即:
(6)
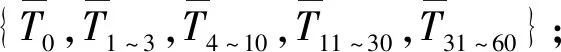
3 ACO-BP神经网络模型
3.1 ACO-BP神经网络模型
Dorigo博士于1991年利用蚁群活动规律创建蚁群算法,其正反馈、分布式计算和全局寻优等特征使其在数据挖掘、模糊建模、群体智能等领域得到广泛应用[11-15]。将蚁群算法引入到BP神经网络模型对网络连接参数进行优化,即ACO-BP神经网络模型。BP神经网络模型存在易陷入局部极小等不足,针对土石坝竖向位移动态变化的非线性特性,建立基于蚁群算法改进的3层反向迭代传播神经网络模型,该模型结构见图2。
利用蚁群算法(ACO)全局寻优能力为BP提供σ(σ≥1)较优的初始权值组合,来克服BP算法对初值设置较敏感、易陷入局部最优的缺点;再利用BP算法梯度下降的原理进一步“细调”权值,寻找网络真正的全局最优点,来克服由于对定义域进行分割带来的量化误差及单一蚁群算法训练网络耗时过长的不足。样本数据经隐含层学习后,经输出层(output layer)传递函数(Purelin)训练生成大坝位移和3个影响因素之间的关联性数据集。
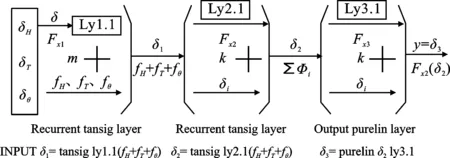
图2 基于蚁群算法改进的ACO-BP网络模型
3.2 ACO-BP神经网络算法流程
将蚁群算法(ACO)引入到BP神经网络模型对网络连接参数进行优化,其逻辑判断流程见图3。
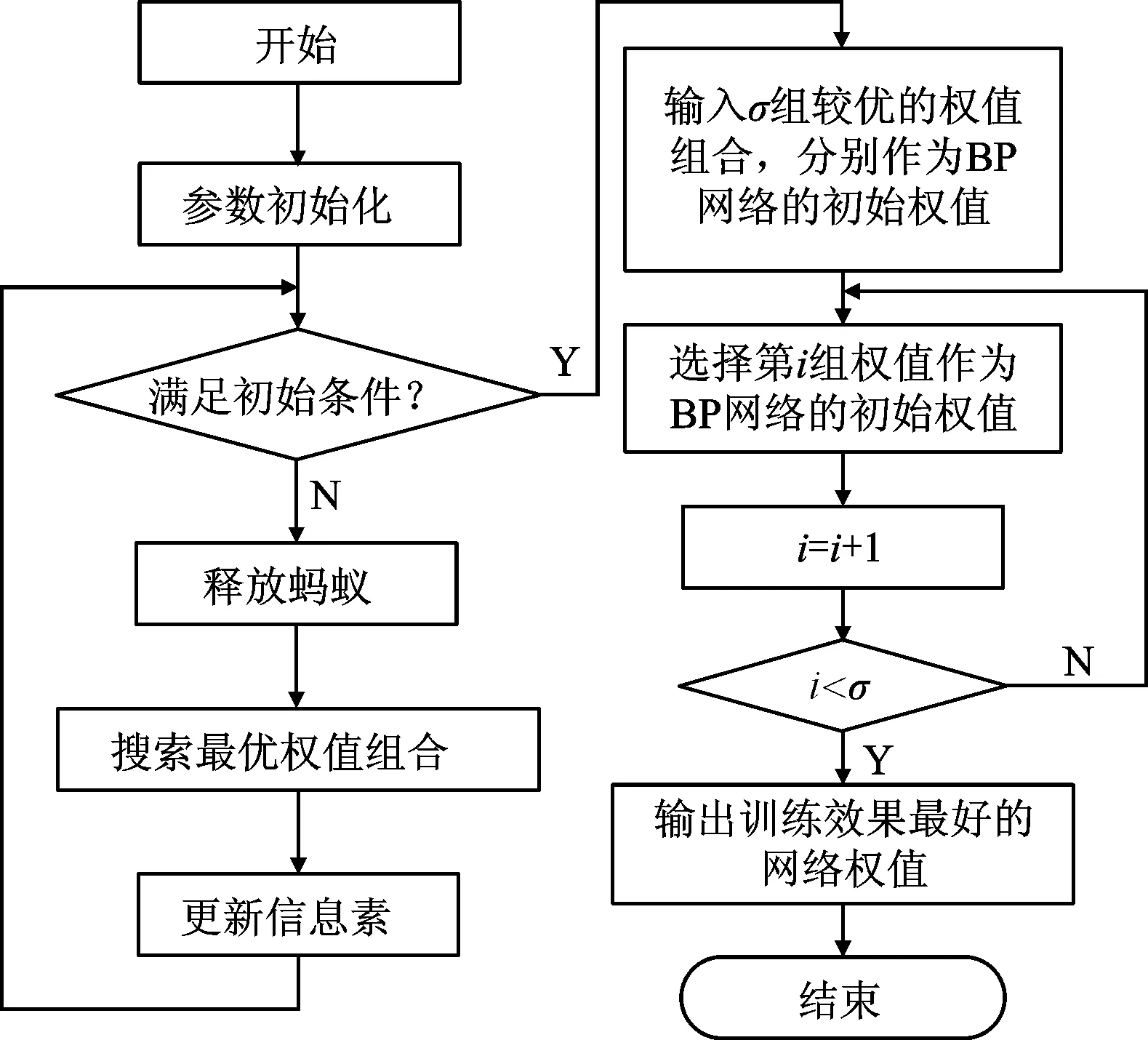
图3 ACO- BP网络模型逻辑判断流程
采用ACO-BP方法训练神经网络的步骤为:ACO-BP神经网络通过初始化、神经网络参数选定、信息素调节等步骤的不断重复,使所有路径收敛为一条路径,通过计算网络输出误差值和实际输出误差值对比,找到局部最优解;计算获得误差满足要求的全局最优解,否则重新寻优。该方法克服了BP神经网络易陷入局部最优的缺点。
4 算例分析
4.1 工程概况
某大坝为碾压式心墙土石坝,最大坝高105.30 m,坝长297.40 m,水库库容5.21×108m3,校核洪水位708.80 m,正常蓄水位704.00 m。工程以发电为主,兼顾防洪、灌溉、养殖等功能。1983年,总体工程竣工验收。大坝安全定期检查,观测项目主要有渗流、坝体变形、应力应变观测[16-17]等。运行检查实测坝体浸润线均较低,防渗结构设计整体符合规范要求,施工质量优良。
4.2 大坝位移监测
因在坝体变形中,以竖向位移(沉降量)为最大[18],所以本文主要对坝体竖直方向位移监测数据进行分析,优选监测数据较完善、资料代表性较强和综合性较全面的大坝下游坝肩处的D7-2、D8-2、D9-2共3个测点,对其2016年7月12日-2016年11月30日之间的监测数据进行分析预测。大坝竖直方向位移各监测孔布置位置见图4,D7-2、D8-2、D9-2 3个测点的位置及变形参数见表1。采用坝壳位移监测中下游7.8 m处D7-2、D8-2、D9-2 3个变形测点的竖向位移及相应水位、温度和时效等数据资料作为学习样本训练ACO-BP网络模型。
4.3 BP网络模型构建
(1)输入、输出量的确定。根据土石坝位移监测内容及特点,选择包含输入层、隐含层和输出层的3层神经网络结构[19-20]。测点布置选取温度分量因子5个,水压分量因子3个和时效分量因子2个,共10个预报因子,即神经网络模型输入层节点数为10;输出量为大坝竖向位移。
(2)隐含层节点数的确定。运用MATLAB软件,训练次数为50 000,在[k-2,k+2]区间找出最佳隐含层节点数,对每个节点数分别测试5次后,算出平均次数。其中,测点D7-2不同神经元个数实测数据的网络预测误差见图5,训练次数见表2。

表1 大坝下游坝肩D7-2、D8-2、D9-2 3个测点的位置及变形参数

图4 土石坝变形位移监测测点布置图(单位:m)
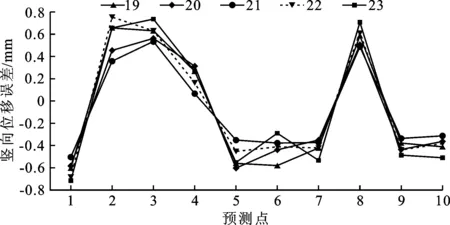
图5 D7-2测点不同隐含层节点数竖向位移预测误差对比

表2 不同隐含层节点数的训练次数
从图5和表2不同神经元个数预测误差对比分析可知:选取隐含层节点数为21,其在5个节点组合中平均训练次数最少,为18 369,网络预测误差也相对较小,训练次数较少,收敛速度较快。
4.4 ACO-BP网络模型参数
ACO-BP网络进行蚁群优化编码定义为矩阵Matrix_wb,通过自动寻优获得与连接权值和阈值矩阵维数相等的信息素矩阵Matrix_phe,对应每只蚂蚁选的权值矩阵为Matrix_w;权值位置矩阵为Matrix_place。3层BP神经网络主要结构参数为:输入层神经元数为10,隐含层神经元数为21,输出层神经元数为1,故寻优规模=10×21+21×1+21+1=253[10],权值区间的最小值Wmin=-1,最大值Wmax=1;最大迭代次数500,信息启发式因子α=1,期望值启发式因子β=1。ACO-BP网络模型参数设置见表3。

表3 ACO-BP网络模型参数设置
对坝体D7-2、D8-2、D9-2 3个变形测点,采用MATLAB 2016软件按表3参数指标编写ACO-BP网络模型预测程序,并经样本学习训练后生成对应预测数据,对大坝变形位移进行预测。
4.5 模型预测结果分析
坝体D7-2、D8-2、D9-2 3个测点安全监测数据分别采用BP网络模型及ACO-BP网络模型,针对竖向位移样本进行学习训练和对比分析。限于文章篇幅,仅展示D7-2测点分析结果,其监测数据经ACO-BP模型学习训练后,采用MATLAB软件运算生成的拟合曲线,见图6。D7-2测点实测值与预测值间的数值对比见图7和表4。
从图6、7和表4可知,D7-2测点网络模型输出的预测拟合值与实测值总体变换趋势一致,拟合效果较好。个别数据点存在拟合精度偏低问题,主要是模型处于不断自学习过程,不影响全局寻优预测。3个测点的安全监测数据采用BP和ACO-BP两种模型处理后,其预测精度对比详见表5。
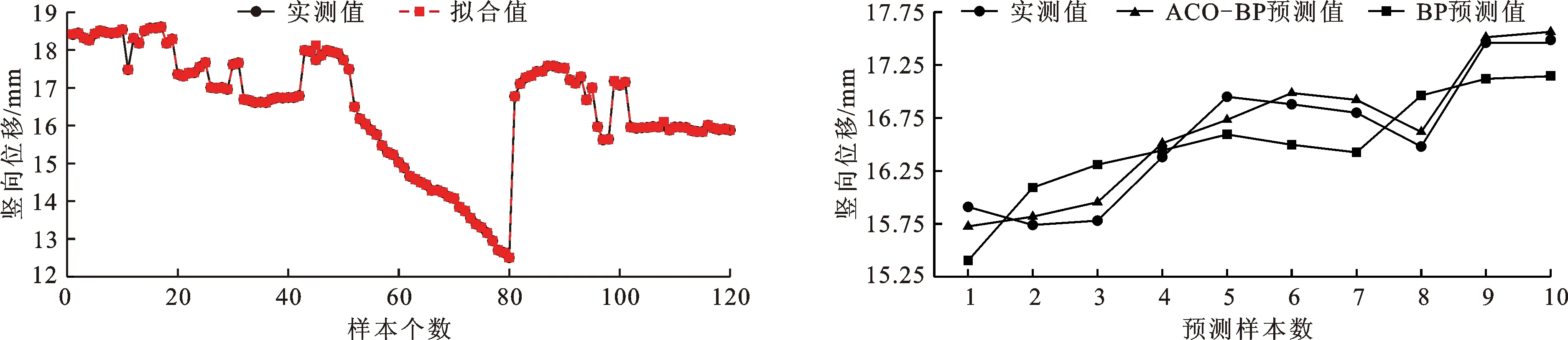
图6 D7-2测点竖向位移ACO-BP网络模型拟合曲线 图7 D7-2测点竖向位移不同模型预测值与实测值对比
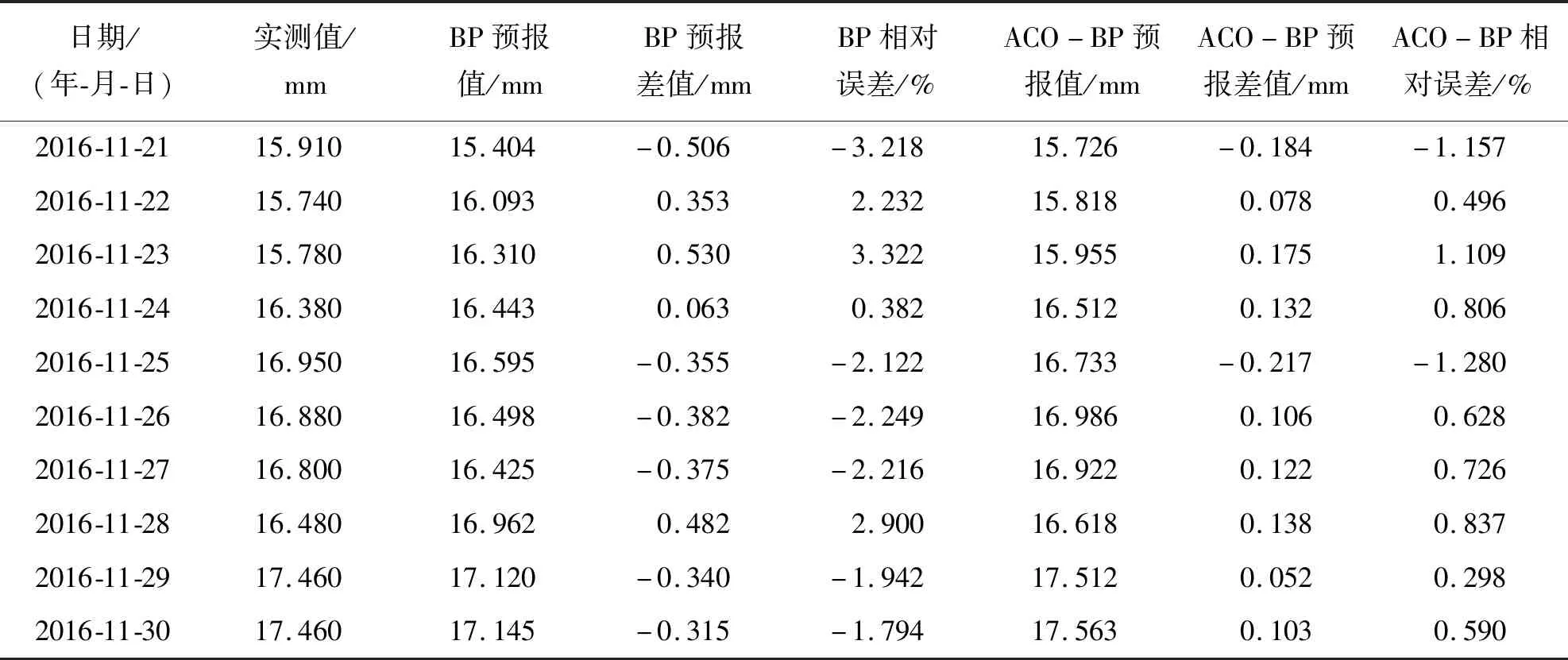
表4 D7-2测点竖向位移BP和ACO-BP两种模型预测结果与实测数据对比

表5 3个竖向位移测点的BP和ACO-BP两种模型预测精度对比
由表5可知,参数条件相同的情况下,ACO-BP网络模型预测值的均方误差、平均绝对误差、平均相对误差均小于BP网络模型的相应数值,且ACO-BP模型对样本训练具有更好的逼近能力,更易于收敛。
5 结 论
大坝变形位移监测ACO-BP网络模型通过引入蚁群算法,全局寻优BP网络连接权值和阈值来拟合和预测大坝变形位移发展规律,确保土石坝安全监测预报更为准确可靠。通过工程实例分析,得出以下结论:
(1)ACO-BP网络模型在寻参过程中,采用ACO蚁群算法对多层网络隐含单元的连接权值和阈值进行训练优化,既能发挥蚁群算法的正反馈优势又能实现全局寻优,避免陷入“超前”或“滞后”的局部极小值寻优,加快了BP网络最优解的收敛速率。
(2)ACO-BP网络模型预测值与实测值的相对误差相对于BP网络模型有了明显减小,在相同参数条件下,ACO-BP模型拟合值的均方误差更小、预测拟合能力更强、可靠性更高,能更好地适用于大坝变形位移的预测预报。可在此基础上构建多维复杂关联因素的安全预警模型,确保大坝安全稳定服役。
