小型化光纤光栅解调系统设计及寻峰算法的模拟评测

孙杉杉，杨 雄，王海勇，姜亚军，杨德兴

（1. 上海航天设备制造总厂有限公司，上海 200245；2. 西北工业大学 理学院，陕西 西安 710129）

引言

光纤光栅在光通信尤其是光纤传感领域得到了广泛应用，因其具有体积小、质量轻，抗腐蚀和抗电磁干扰等优点[1-2]，特别适合精密复杂的应用，如石油化工、航空航天及土木工程中的结构健康监测[3-4]、运行状态检测[5-6]、大坝渗流监测[7]、导弹冲击波和爆炸中的压力分析[8-9]，以及智能服装、硅光子集成芯片[10-11]等。光纤光栅特别是光纤布拉格光栅（fiber Bragg grating，FBG）容易通过不同形式的复用技术组成大规模的分布式多参量传感网络。这种分布式传感技术具有定位准确、传感精度高的优势，有望在大型航天器结构件的地面试验和在轨监测中发挥重要作用。要实现大规模多参量光纤光栅传感网络，需要有功能强大的光栅信号解调系统，用于航天在轨监测还需具有解调精度高、动态范围大、耐冲击、低功耗、体积和质量小等特点。全固态封装CCD 光谱解调模块的出现。为研制符合上述要求的解调系统提供了必要条件。这种模块将光谱信号在空间上展开，由离散的CCD 像元进行采集，每个光栅的反射谱仅有3～5 个采样点，不能直接获得光谱峰。因此，需要合适的算法从3～5 个采样数据快速准确地寻找到峰值，从而获得高精度的解调结果。光谱解调模块的工作模式不同，如工作环境、工作频率、信号转换方式等，需要合适的处理速度和精度，因此，应针对具体应用采用合适的寻峰算法。通常需要将寻峰结果与更高等级的仪器进行对比才能确定其测量精度。本文提出了一种只依靠软件模拟方法即可对寻峰算法的优劣进行评测，为研制过程中选择合适的寻峰算法提供了依据。

1 FBG 传感原理简介

图1 为FBG 工作原理示意图。由宽带光源发出的光通过光纤入射到FBG，其中满足布拉格条件的窄带光波受到反射，对应的透射光谱呈互补凹陷状，具有对称分布特征，因此，可将其中心波长视为反射谱峰值波长。

FBG 的本征传感量为应变和温度，满足：

式中： ∆λ=λ−λ0为FBG 在受到应变和温度变化时，其反射谱中心波长的变化量，λ 为FBG 受到应变作用或温度变化时的中心波长，λ0为初始中心波长；Δε 和ΔT 分别为应变和温度的变化量；Kε和KT分别为应变和温度的灵敏度系数[12]。

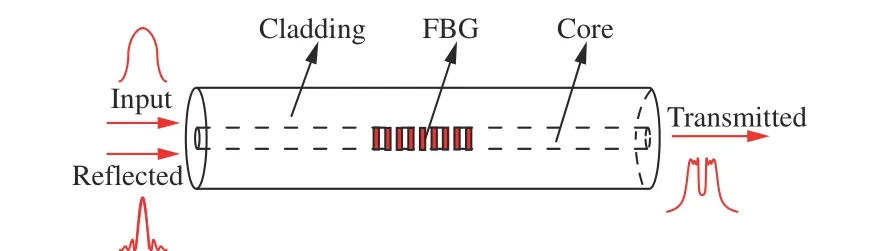
图 1 FBG 工作原理示意图Fig. 1 Schematic diagram of FBG working principle

2 光纤光栅解调系统

采用全固态封装CCD 光谱解调模块为核心组成的解调系统主要包括光学模块、电学模块和上位机软件3 个部分。光学模块包括宽带光源、光纤环形器以及解调模块的光学部分，电学模块包括开关电源、通讯控制板、解调模块的电学部分，上位机软件用于传感信号的处理、显示及存储。

2.1 解调模块

本解调系统采用BaySpec 的光纤布拉格光栅分析模块（FBGA）作为解调模块，其解调光谱范围为1 525 nm～1 565 nm，响应时间小于0.6 ms，波长分辨率为1 pm，最大采样频率5 kHz，体积为96 mm×68 mm×15.8 mm，探测器含512 像素，内部无机械活动部件，能实现复杂环境下对光谱信号的同步测量[13]。

2.2 解调系统的工作原理

解调系统的组成如图2 所示。由开关电源模块为系统提供5 V 直流电，ASE 光源发出的宽带光从端口1 进入光纤环形器，通过端口2 输出，传输至FBG 传感阵列中，传感阵列中各FBG 的反射光波通过端口2 进入环形器，由端口3 输出，并传输至FBGA 进行光谱分离和探测。FBGA 中包含准直透镜、色散单元、聚光透镜、探测阵列。探测阵列输出的电信号通过DSP 处理后置于存储器中等待访问。通信模块一方面为FBGA 供电，一方面通过RS232 串口与FBGA 建立通信，通过发送指令接收存储器中的数据，完成信息交互。最后上位机软件通过调用指定命令代码直接操作该模块，并对采集的数据作进一步处理。

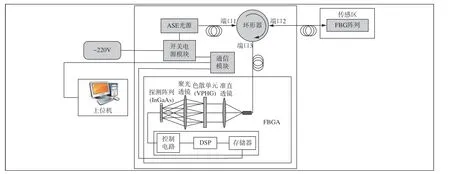
图 2 解调系统的工作原理Fig. 2 Working principle of demodulation system

3 软件编写及界面设计

上位机监测软件的基本功能是通过发送特定的通信命令从解调模块中循环提取采集到的光谱数据，然后运用寻峰算法得出对应的中心波长并保存所得数据，最后将采集到的光谱数据和计算得到的波长数据分别以图表的形式显示出来，供用户分析，软件的基本工作流程如图3 所示。

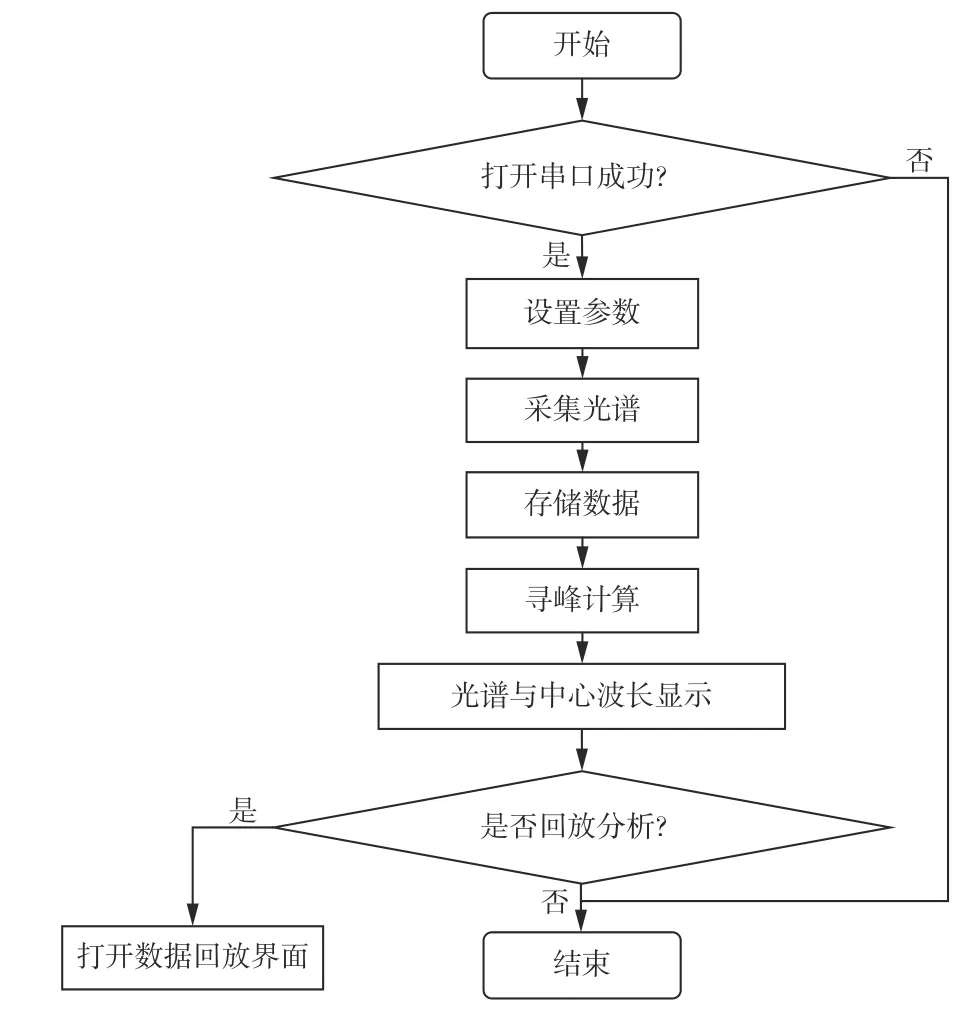
图 3 上位机软件工作流程图Fig. 3 Flow chart of PC software work

上位机软件分别主要由配置、采集、监测、保存、回放5 个程序模块组成。其中配置模块可对寻峰算法类型、曝光时间、最大扫描速率等进行设置，采集模块通过发送命令将经过光电转换的电信号从FBGA 中读取出来，监测模块的作用是将采集到的实时光谱及波长数据通过图表显示出来，保存模块将光谱及中心波长数据保存在指定文件中，回放模块可将保存的数据以图表的形式重现以便后期处理。上位机软件的主界面如图4所示。主界面包括监测、FFT、回放和配置4 个部分。

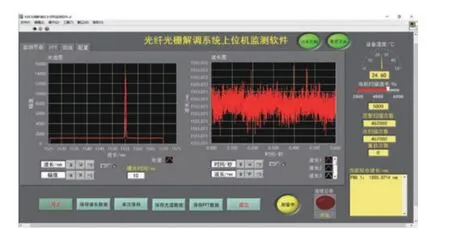
图 4 上位机软件主界面Fig. 4 User interface of PC software

4 光谱反射峰的确定

峰宽约为0.2 nm～0.3 nm 的FBG 反射谱，在各种干扰因素的影响下，峰值会有跳动，离散采集的最大值不能代表FBG 的真实中心波长，会存在较大偏差[14]。常用的去噪方法有小波去噪法、滤波法等[15]，同时还可采用多次平均的方法降低随机误差。因此，还需要适当的寻峰算法通过有限的离散数据找到峰值位置，以提高精度。

常用的寻峰算法主要有质心法、高斯拟合法、多项式拟合法、径向基函数拟合法、三次样条插值拟合法和半峰检测法等。其中，径向基函数拟合法测量精度最高，但在实验数据较多时，需要较长的计算时间，不适合实时运算[16]，而三次样条拟合法敏感度较低，半峰检测法抗噪性能较差[17]，质心法稳定性差，低阶多项式拟合法准确性较差，高阶多项式的运算量太大，不适于实时监测。经比对后，本文采用综合性能较优的高斯拟合法。

4.1 高斯拟合法

正常的FBG 具有对称的反射峰，高斯函数线型与其相似。采用高斯函数对FBG 反射峰进行拟合，虽然不能准确复原峰形，但却可以较高精度获得传感所需峰位。以高斯函数表示的反射峰光谱分布可写为

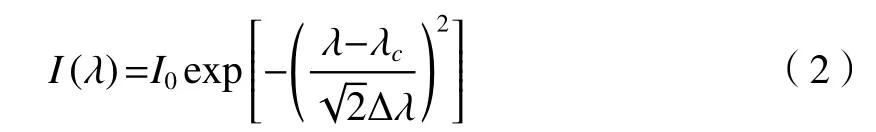
式中：I0为反射谱的峰值强度； λ为反射谱中心波长； ∆λ为表征高斯函数特征宽度的常量。对峰值采样点运用最小二乘原理进行拟合，得到的高斯函数峰值所处位置即为反射谱的中心波长。

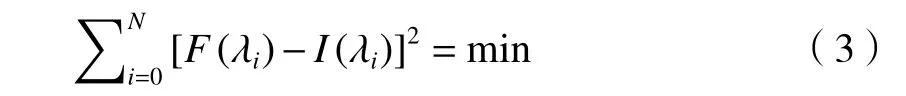
式中F（λi）和I（λi）分别为反射峰的实际采样值和期望值。

4.2 寻峰算法的仿真评测

不同的寻峰算法产生误差的形式不同，误差大小各异，而且还与采样点数量、噪声类型及信噪比有关。严格来讲，算法优劣和误差大小应该通过计算结果与标准值的比对进行评测，但这种方法的低效率、高成本，使其不适合在解调仪的开发过程中采用。本文提出一种利用计算仿真的实验室评测方法，通过软件构建一个标准的FBG 反射谱函数，对其叠加噪声后按解调仪探测阵列的实际参数进行离散采样，然后通过寻峰算法获得FBG 的中心波长，通过与标准函数中心波长的比对实现对寻峰算法的评测。

如图5 所示，首先通过软件生成一个FBG 标准反射谱，其中心波长为1 550.000 nm，半峰全宽（full width at half-maximum，FWHM）为0.19 nm（可 调节），然后根据光谱阵列探测器的像素尺寸与光谱分布的关系，并让标准谱的峰值波长位于一个像素的中心，取每个像素范围内数据的平均值作为该像素点的功率值，得到由11 个离散数据点组成的对称采样谱。一般来说某窄带波长的功率值需要通过对宽带光源的输出功率谱进行积分计算才能得出，但为了便于模拟计算，将采样峰值设为100 μW。

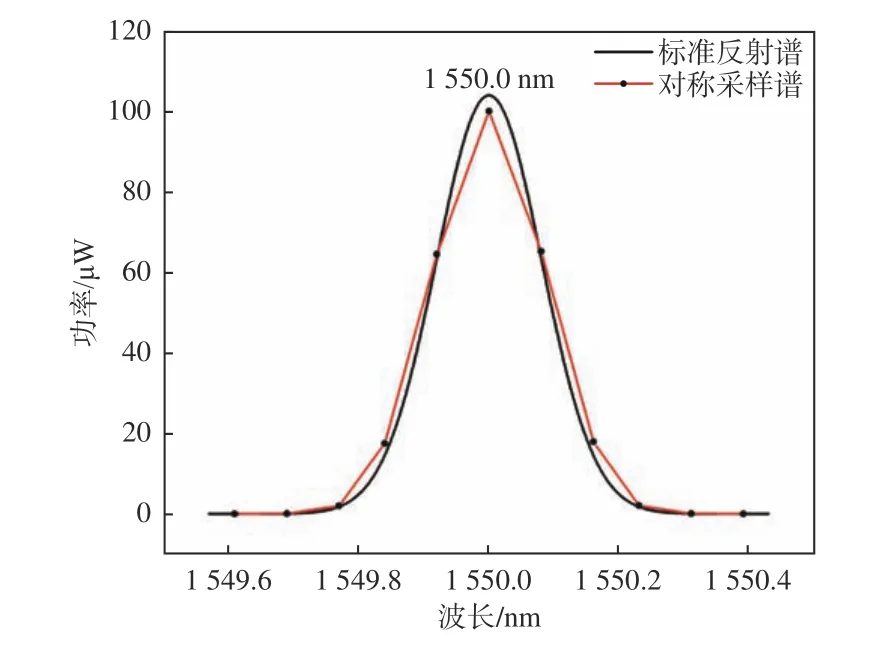
图 5 标准FBG 反射谱Fig. 5 Standard reflection spectrum of FBG

为了模拟实际情况，在整个探测光谱范围内叠加标准差为1.4 μW 绝对值的随机功率噪声，并在波 长 上 叠 加 标 准 差 为1.7×10−3nm 的 随 机 波 长 噪声，这2 种噪声分布如图6 所示。

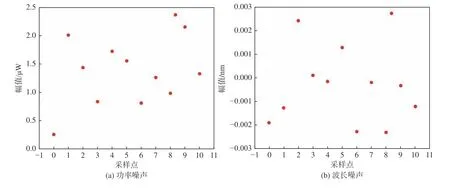
图 6 功率及波长噪声分布图Fig. 6 Distribution diagram of power and wavelength noise

在测试中通过调节标准光谱的功率来改变峰值信噪比，图7 为叠加功率噪声和波长噪声后，2 种信噪比下的模拟光栅反射谱。

信噪比的大小决定了噪声对光谱的影响程度。本文将信噪比分为高、低2 个范围进行比较，高信噪比包括20、30、40、50，低信噪比包括4、6、8、10。通过设定阈值对光谱数据进行过滤，只取功率大于阈值的数据进行拟合寻峰。

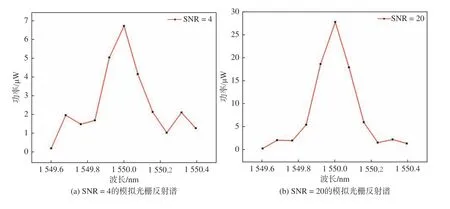
图 7 模拟光栅反射谱Fig. 7 Simulated grating reflection spectrum

阈值（Threshold，Th）的选择受限于噪声的水平，故在评测中将Th 设为噪声平均值的整数倍，低于Th 的采样数据在寻峰计算中予以舍弃。过小的Th 无法有效滤波，而过大的Th 容易去除掉反射谱中的有效数据点，分别将Th 设为1、2、3、4，模拟不同Th 下拟合波长误差与信噪比的关系。

Th=1 时，虽然能保留较多采样点，但存在受噪声影响较大的数据点，这会使拟合结果误差不稳定；Th≥3 时，虽然能保证滤波后的数据受噪声影响小，但过高的阈值会将反射谱中一些较小的数据点一起去除，使有效采样点变少，拟合的中心波长误差反而会变大；当Th=2 时，几乎可以过滤掉所有受噪声影响较大的数据点，且能保留足够的有效采样点，不会对寻峰造成过大的误差。模拟结果如图8 所示，Th=2 时的中心波长误差分别为6.9 pm、4.9 pm、3.9 pm、3.3 pm，其拟合结果最接近标准值。从图8 中可以看出，更大的SNR 可以得到更准确的光谱数据，拟合误差与信噪比近似成反比，且Th=2 时拟合寻峰效果最好。

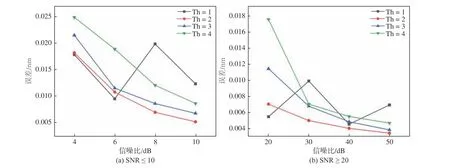
图 8 不同Th 下中心波长误差与信噪比的关系Fig. 8 Relationship between error of center wavelength and SNR under different Th

设定FWHM 分别为0.13 nm、0.19 nm 和0.28 nm的标准FBG 反射谱，叠加噪声后FWHM 范围内分别包含约2、3、4 个数据点。当Th=2 时，模拟计算不同FWHM 下中心波长误差与信噪比的关系。

反射谱峰的宽度限制了有效采样点数量，3 种FWHM 的模拟反射谱经过阈值过滤后分别存在约3、5、7 个有效采样点。如图9，对于FWHM=0.19 nm 的FBG，当SNR 分别为20、30、40 和50时，拟合波长误差分别为7.5 pm、4.2 pm、3.5 pm和3.0 pm。

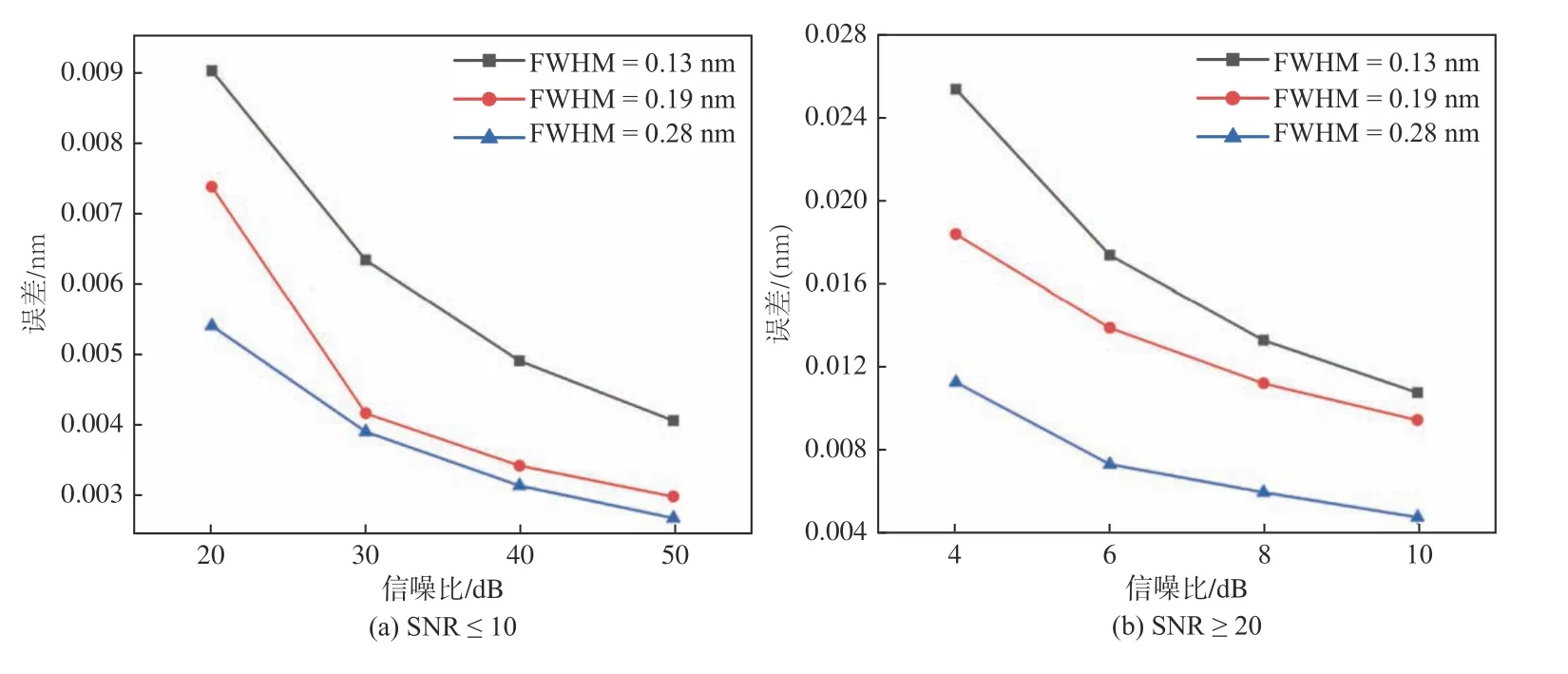
图 9 不同FWHM 下中心波长误差与信噪比的关系Fig. 9 Relationship between error of center wavelength and SNR under different FWHM

5 实验对比验证

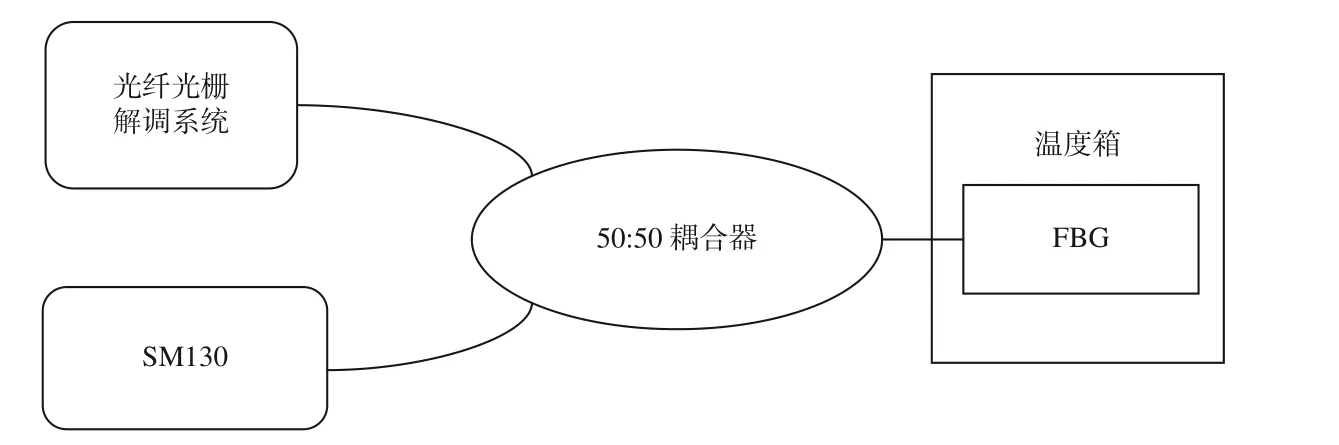
图 10 实验系统示意图Fig. 10 Schematic diagram of experimental system

为了测试解调系统的稳定性与精度，将半峰宽约为0.19 nm 的FBG 置于温度稳定性为0.1 ℃的温控箱中，采用50:50 的光纤耦合器将从FBG 反射的光分为2 路，一路连接Micron Optics 生产的分辨率为1 pm，稳定性为2 pm 的高精度光栅解调仪SM130，以其提供的波长作为标定值，另一路接入本文设计的光纤光栅解调系统，光路如图10 所示。

温控箱的温度变化为20 ℃～100 ℃～20 ℃，每隔10 ℃维持30 min，期间持续记录数据。分别取温度2 次恒定在30 ℃时的100 个有效数据，解调结果如图11 所示，中心波长集中在（1 543.068 9±0.001 4）nm 范围内，则解调系统的稳定性为±1.4 pm。

计算解调系统和SM130 在各温度下波长的平均值并进行比较，结果如图12 所示。分别对两组数据做线性拟合，SM130 和解调系统的R2分别为0.999 72 和0.999 70，灵敏度分别为0.029 5 nm/℃和0.029 6 nm/℃，解调系统中由温度波动造成的误差为2.95 pm，故二者的真实误差应为8.84−2.95=5.89 pm，综上说明，本文研制的解调系统具有很好的线性度且精度约5.89 pm。

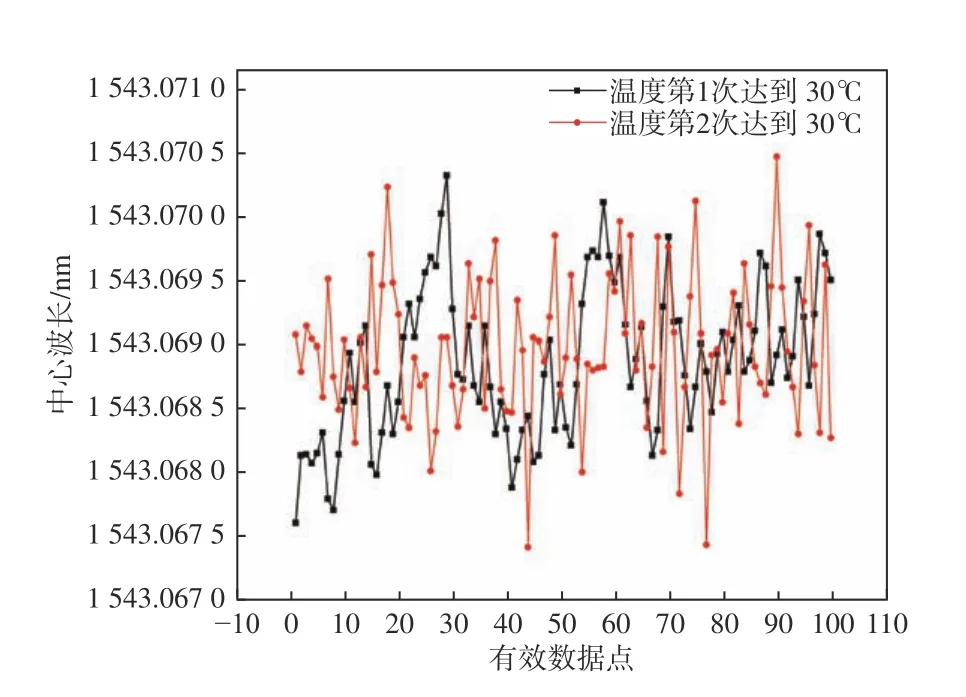
图 11 30 ℃时的解调结果Fig. 11 Demodulation results at 30°C

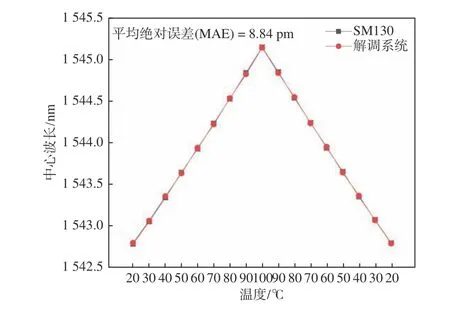
图 12 不同温度下解调系统与SM130 结果比较Fig. 12 Comparison of demodulation system and SM130 at different temperatures

6 结论

本文从小型化的光纤布拉格光栅解调系统的硬件组成入手，对其工作原理进行了较为深入的研究，设计了同时具有数据采集、处理、显示、存储及回放功能的上位机软件。同时，为了改善解调系统的解调精度，以高斯拟合法作为寻峰算法，在计算机上模拟并分析对比了在不同FWHM、Th 和SNR 情况下中心波长的误差，论证了高斯拟合法对解调精度的提升，并在对比实验中得到了验证。在该小型化光纤光栅解调系统中，上位机软件中使用高斯拟合法作为寻峰算法模块，可以使其解调精度更高。