不同插值算法的光场重聚焦分析

常 青，赵双明

（武汉大学 遥感信息工程学院，湖北 武汉 430079）

引言

光场[1]的概念在1936 年被提出，用于描述光在空间中的分布特征。在后期发展中，七维光场[2]被提出，用来描述光线在空间中任意时刻所在的位置，可以用七维全光函数形式表示。七维全光函数记录的光场数据量过大，使得光场数据的采集、记录、存储都存在较大的难度，应用和发展受到了极大限制。因此，在不考虑光线传播途中频率的变化，任意时刻的光线可以用五维光场[3]表示。直到1996 年，人们开始用四维光场[4]的概念记录光线的位置和方向信息，目前比较常用的是双平面参数法，该方法采用记录两个平行平面上两点来记录光线的空间位置和方向信息，如图1 所示。

光场数据的采集可以分为相机阵列和光场相机两种，相比于多相机阵列使用的规模限制，光场相机在实际生活中更易得到广泛使用。光场相机[5]又称全光相机，与传统相机相比，光场相机在记录光线强度的同时，还记录了光线的位置和方向信息。2005 年，Ren 研制出了一款手持光场相机[6]，可以增强光场相机的便携性，其特殊设计在于将传感器安装在微透镜阵列的焦平面上以减少渐晕效应。将光场相机采集到的四维光场数据进行数字处理，可以得到其景物的深度信息。目前，光场相机在图像重聚焦、三维重建、目标识别和场景监控等方面得到了广泛应用。

近年来，在光场数据的获取、重聚焦，以及三维建模方面，国内外学者做出了诸多研究。利用传统相机在一次拍摄中获取多模态图像进行图像合成[7]。为了提高光场相机采集数据的精度，需要将微透镜阵列和探测传感器进行配准和误差分析[8]，在光场数据处理中，可以从光学器件方面建立像素光场与标准光场之间的联系，进行光场相机的标定[9]；模拟奇异的显微镜照明模态并以数字方式校正光学像差[10]；采用点扩散模型对光场模型进行分析评测[11]；对于稀疏的光场数据采样，采用启发式数据插值的方法可以消除锯齿效应[12]，通过极平面图像分析视差估计图，降低视差匹配中的成本[13]。对于光场数据的频域重聚焦，通过零填充增强图像的可见性和分辨率[14]，采用角度分辨率进行换算增大其空间分辨率[15]。

光场相机是目前较为常用获取四维光场数据的方法之一，相比多相机阵列方法，其适用范围更为广泛。根据成像方式不同，目前常用的光场相机可以分为针孔成像和微透镜成像两种。相比于针孔成像，微透镜对光场的记录更为完整，因此在实际应用中更为广泛，其相机成像模型如图2 所示。

对于光场数据重聚焦，本文采用了已面向市场的Lytro 全光相机[16]获取的光场数据，使用MATLAB进行数据重聚焦实验。通过实验，对不同插值方法的空间域和频域重聚焦的效果和速率进行对比分析，在满足像质要求的情况下，选择速率最高的方法进行重聚焦。

1 空间域重聚焦插值算法

1.1 空间域重聚焦原理

空间域重聚焦（spatial domain refocusing），是依据光场相机成像模型得到的。传统相机在拍摄过程中，可以通过改变主透镜到传感器的距离改变对焦深度。而光场相机记录了光线的四维空间信息，可以在拍摄完成后，通过数字处理完成不同深度的对焦，即“先拍照后对焦”。通过重采样的方法获得四维光场数据，以二维情况进行讨论分析，重聚焦模型如图3 所示。

图 3 光场相机重聚焦模型Fig. 3 Light field camera refocusing model

图中，L 为采集到的光场，U 和S 分别表示主镜头孔径所在平面和微透镜阵列所在平面，两个平面之间的距离为F。选择新的对焦平面S′，与U 面之间的距离为F′，令 F′=αF。重聚焦平面S′面上所成的像等于US′之间光场的积分，即：

从（1）式中可以看出，数字对焦就是对光场聚焦面的深度进行平移调节后，在方向维度进行积分的过程。可以推广至四维光场，获得的重聚焦能量值为

空间域积分重聚焦就是在采集到的四维光场数据上，通过不同的 α值平面确定不同深度的重聚焦平面，分别对远近不同的物体进行聚焦。根据相机成像原理，不同景深对应的焦平面成像效果如 图4 所示。

图 4 相机聚焦模型Fig. 4 Camera focusing model

根据景物的不同景深，在相机的焦平面成像的过程中，焦平面前移，后景在焦平面上清晰成像，焦平面后移，前景在焦平面上清晰成像。根据不同 α聚焦不同的景深，其近景、远景的重聚焦效果如图5 所示。

图 5 重聚焦图像Fig. 5 Refocusing images

由图5 可以看出，该重聚焦方法对远处和近处景物清晰度的变化取得了较好的结果，但是当焦距景深缩小时采集到的景物范围变小，而焦距景深增大，整体图像缩小使得图像整体清晰度降低。该方法对原始数据的利用率较低，将采样点在微透镜阵列上的坐标系数等比例缩放，通过变形公式使重采样图像的大小与原始图像大小一致，重采样公式为

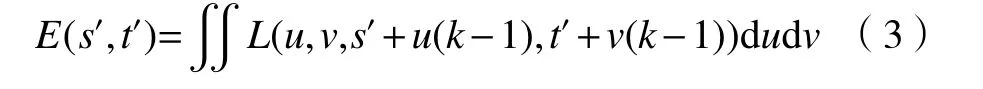
图 6 变形公式重聚焦Fig. 6 Deformation formula refocusing

根据其几何原理，对相应二维情况进行分析，可以得到该方法重聚焦的焦平面位置以及聚焦情况。该方法重聚焦方式如图6 所示。 图中该新聚焦平面的聚焦深度与原调节参数 α的关系是： k=2−。由此可以计算出，当原模型采用 α=1.2进行重聚焦时，其聚焦景深与改进模型参数k=2−=1.167时一致，将这两种形式对应相同实 际聚焦平面的情况进行对比，如图7 所示。

图 7 两种重聚焦效果对比Fig. 7 Comparison of two refocusing effects

根据对比分析，在取得同样聚焦深度时，与原重聚焦模型相比，改进公式重聚焦影像不改变图像的大小和成像范围，同时对原始数据利用率更高。

1.2 空间域不同插值算法实验分析

在实际光场图像重聚焦中，四维光场数据由离散点组成。在空间域重聚焦积分前，对微透镜阵列上每一个透镜对新聚焦平面上每一点的光照影响需要进行插值计算。常见的插值方法有：临近点插值（nearest）、线性插值（linear）以及三次Hermite 插值（cubic）。

在一维插值中，临近点插值法的原理是从采样点左右样本点中，选择距离较近点的值作为采样点的值；线性插值是根据左右样本点与采样点的距离作为权值求和，3 个点满足线性关系；三次Hermite 插值根据左右样本点的值和采样点位置，计算其一阶导数，并采用基函数的方法构造其插值函数。3 种算法中，临近点插值计算复杂度最低，插值结果误差最大；三次Hermite 插值复杂度最高，插值结果精度最高。

对于同一图像，在相同重聚焦深度情况下，分别采用这3 种插值方法进行实验分析，并比较多次重采样的效率。在k=1.2 时，成像效果如图8 所示。为了对重聚焦效率进行更为清晰的分析，分别进行1～10 次的重聚焦实验，实验结果对比如图9所示。

图 8 空间域不同插值方法重聚焦效果Fig. 8 Refocusing effects of different interpolation methods in spatial domain

图 9 3 种插值方法耗费时间对比Fig. 9 Time-consuming comparison of three interpolation methods

通过图8 直观判断，线性插值法和三次Hermite插值法重聚焦效果能达到基本像质需求。对于不同插值方法得到的重聚焦图像质量进行量化分析，可以采用无参考评价方法（NR）对重聚焦质量进行评估。无参估计无需参考图像，仅通过自身特征来评价图像质量，包括面向特定失真和非特定失真这两种方法。在空间域插值中造成的模糊等 失 真 采 用BIQI（blind image quality index）[17]和NIQE（natural image quality evaluator）[18]无参评价的方法对图像质量进行评估。BIQI 原理是基于小波域的统计特性算法，包括两级框架。先通过支持向量机SVM 识别图像每一种失真的可能性，再通过无参方法计算每一种失真可能性下图像的质量，最好加权平均。BIQI 取值在0～100 之间，值越小质量越好。对这三种插值方法的BIQI 值如表1 所示。NIQE 原理是通过归一统计分析，测量统计特征的改变来评测图像质量。该方法图像的质量得分较高值代表较低质量。

表 1 空间域重聚焦图像质量指标值Table 1 Index value of refocusing image quality in spatial domain

通过实验结果可知，NIQE 值差异较小，BIQI差异较大，两种方法三次Hermite 插值法均最佳。结合成像主观判断可以得出，临近点插值重聚焦效果较差，线性插值法和三次Hermite 插值法重聚焦效果能达到基本像质需求。通过耗费时间量的对比，发现空间域重采样耗费时间与采样方法及聚焦次数密切相关，随着重聚焦次数的增多，三次Hermite 插值法耗费时间将远大于线性插值法。因此，在实际大量数据处理中，采用线性插值的方法在满足精度情况下，重聚焦速率最快。

2 频域重聚焦插值算法

2.1 频域重聚焦原理

频域重聚焦（frequency domain refocusing）的核心思想是傅里叶切片定理[19]。在频率域数据处理中，需要引入傅里叶变换将空间域数据转换为频域数据。傅里叶切片定理表明，将二维图像在一维方向上积分投影结果进行傅里叶变换的结果，与将该二维图像傅里叶变换结果取一维切片的结果一致。可以将其推广至多维变换，其性质表明N 维函数对其进行坐标变换后将其积分投影至M 维进行傅里叶变换，那么这个变换等于对函数求傅里叶变换，然后进行坐标逆变换，最后取该变换的M 维切片，用算子简化表示为

式中：I 表示N 维到M 维的积分投影过程；S 表示将N 维函数降维到M 维过程；F 表示对N 维函数进行傅里叶变换；B 表示坐标变换矩阵；“ ◦”表示数据处理操作的结合。结合空间域重聚焦公式，可以表示为

式中：L 表示四维光场数据；[*]表示对*数据进行处理运算。在频率域重聚焦中，为了方便处理四维光场数据，首先需要将二维傅里叶切片定理延展至多维，然后降维至四维进行四维光场数据处理，就可以在频率域实现光场相机重聚焦。重聚焦的光谱能量为

由（6）式推导得，对光场数据频域处理的坐标公式可以转换为

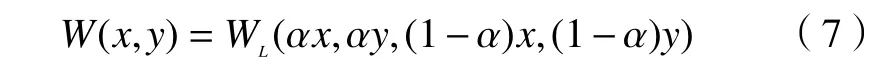
式中 α表示成像焦平面深度改变比例尺，与空间域相同。根据空间域的变形公式，将其带入傅里叶切片定理进行分析计算，可以得到光场数据频域处理模型的改进公式为

通过对比分析，在对四维频域数据取切片的过程中，原模型需要对四维数据均进行插值，而改进模型仅需要在微透镜阵列的二维平面上进行插值取切片。因此，改进公式可以有效提高取切片过程中的计算效率，并降低插值误差带来的影响。

2.2 sinc 插值算法

在一维坐标系中，样本点为 x1,x2,···,xn，对应样本值为 y1,y2,···,yn，使用sinc 插值方法[20]进行采样，采样公式为

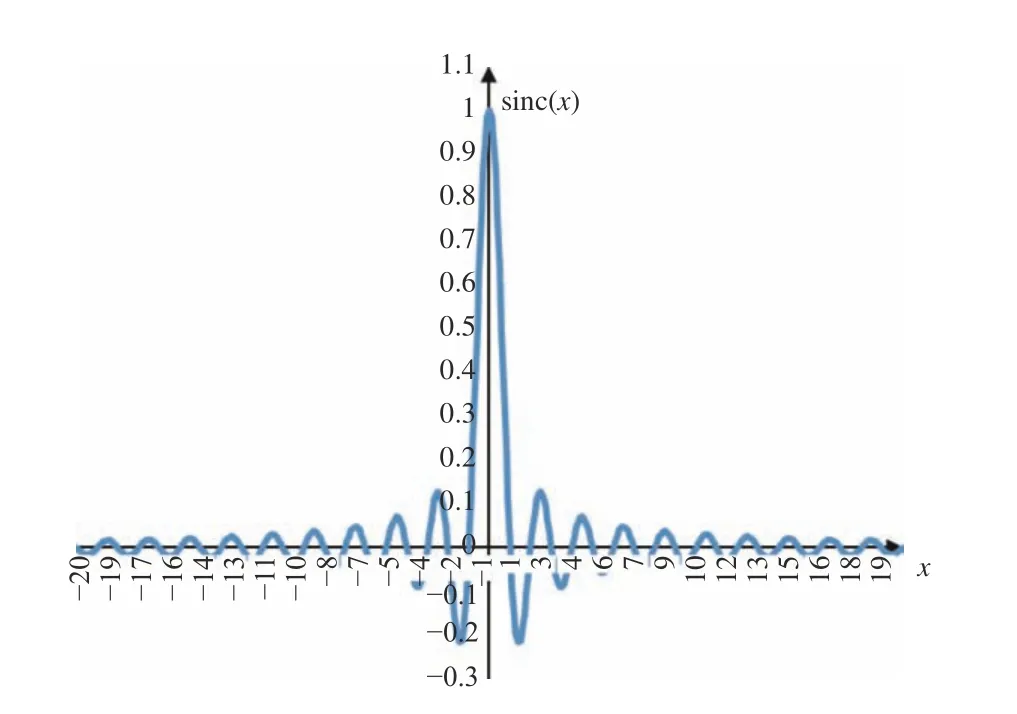
图 10 sinc 函数波形图Fig. 10 sinc function oscillogram

在实际应用中，将所有样本点用于插值卷积会使插值计算量非常大，且随着样本点与采样点距离的增大，其精度的提高很小。通过改变卷积核大小，在满足采样精度情况下，提高计算效率。在卷积核半径为R 时，采样公式为

对光场频域重聚焦取切片的插值方法，可以引入更为理想的插值滤波器sinc 函数。在数字信号处理中，sinc 函数可以使插值后的波谱数据更加平滑，更加接近正弦波形，其带限与光场的空间界限相匹配。随着sinc 插值半径增大，聚焦精度提高消耗时间增大，常用的3 种插值方法相当于插值半径为1 个像素。而sinc 插值的方法忽视了数据空间域中的几何结构，因此对空间域插值方法并不适用。

2.3 频域不同插值算法实验分析

由于四维光场数据的离散性，与空间域相同，频域重聚焦在取切片过程中需要进行插值计算。为了验证插值方法对重采样效果和速率的影响，分别采样常见的3 种插值方法和不同采样半径的sinc 插值法进行实验。对于同一幅影像，在重聚焦参数k=0.85 时，成像效果如图11 所示。

频域插值误差导致图像空间域的误差与图像模糊、噪声等常见的图像失真不同，其对重聚焦后的图像带来伪像的影响，因此对于频域重聚焦影像，常用的无参图像质量评估不能很好地评测图像质量。因此，在这里引用空间域三次插值的重聚焦影像作为参考，以全参考图像质量评估方法峰值信噪比（peak signal to noise ratio，PSNR）和平均结构相似性（mean structural similarity，MSSIM）进行评测。PSNR 是通过计算两幅图像误差判断失真图像质量，值越大代表两幅图效果越接近。MSSIM 根据结构相似性作为评价指标，与SSIM相比，通过多次迭代和滤波采样能更好地与人类视觉感官保持一致，值越大代表两幅图相似度越高。不同插值方法频域重聚焦图像的质量评价指标值如表2 所示。

图 11 频域不同插值方法重聚焦效果Fig. 11 Refocusing effects of different interpolation methods in frequency domain

表 2 频域重聚焦图像质量指标值Table 2 Index value of refocusing image quality in frequency domain

根据实验结果分析，由于光场数据的离散性，在傅里叶切片计算过程中会产生误差，导致重聚焦图像中产生伪像，严重影响重采样效果。因为在傅里叶变换中，频率域的微小误差会对其逆变换之后的空间域造成较大影响。插值误差对频率域的影响远大于对空间域的影响，因此，对空间域而言，双线性插值法即可达到较为良好的效果，而对频域重聚焦，采样sinc 插值法半径足够大时可以有效降低伪像的干扰，对提高精度有明显效果。

由于频域重聚焦耗费时间量主要在于傅里叶变换，傅里叶变换时间约为0.4 s，远大于每一次取切片插值的时间，为了更好地比较插值效率，这里仅分析计算插值所需时间。对于同一张影像用不同插值方法进行多次重聚焦比较其计算效率，对比结果如图12 所示。

图 12 频域不同方法重聚焦效率Fig. 12 Refocusing efficiency of different methods in frequency domain

根据实验结果定量分析和直观判断,三次插值和sinc 插值均能较好地抑制伪像的影响。而插值效率主要取决于插值半径，对同一幅影像不同深度进行多次聚焦时，其效率远高于空间域。在采样半径为3 个像素时去除伪像效果最好，耗时最多。结合插值效率和图像质量，在实际应用中，在满足重聚焦精度情况下，根据所需重聚焦的计算量，sinc 插值函数半径一般选择2 个像素时最佳。

3 空间域和频域重聚焦实验分析

3.1 空间域重聚焦和频域重聚焦对比分析

实验对比分析，在满足精度的同时还需考虑插值效率的影响。空间域计算复杂度主要在于插值及对插值结果进行积分，频率域的计算复杂度主要在于傅里叶变换和插值运算。为了比较空间域和频域不同插值方法重聚焦方法的效果，分别选取基于cubic 插值的空间域重聚焦、基于cubic 插值和基于sinc 插值（插值半径为2 像素）的频域重聚焦，对不同影像采用这3 种方法进行聚焦，采用无参评价BIQI 和NIQE 指标值对重聚焦图像质量进行评估。重聚焦效果如图13 所示，其无参评估指标BIQI 和NIQE 值如表3 所示。

图 13 三种重聚焦方法的重聚焦效果Fig. 13 Refocusing effects of three refocusing methods

表 3 重聚焦图像质量指标值Table 3 Index value of refocusing image quality

实验结果表明，采用适当插值方法，空间域和频域重聚焦均能得到质量较好的图像。改进后基于半径为2 像素的sinc 插值优于常用的三次插值，在部分情况下改善效果显著。

3.2 适用性分析

为了验证空间域线性插值和频域改进插值方法后重聚焦方法的适用性，通过实验对多幅光场数据的重聚焦效果进行检验。在这里选择对其他3 幅光场数据进行实验，分别对其远景和近景进行重聚焦，实验结果证明均能得到良好的聚焦效果。其重聚焦效果如图14 所示。

图 14 两种重聚焦方法的远近景重聚焦效果（左：近景；右：远景）Fig. 14 Far-and-close view refocusing effects of two refocusing methods（left：close view，right：far view）

4 结论

本文分析了微透镜阵列光场相机记录的光场数据重聚焦几何原理，以及根据傅里叶切片定理得到的频域重聚焦方法，并采用不同的插值方法，将光场数据分别从空间域和频率域进行重聚焦实验，分析重聚焦效果和计算速率。首先，对于重聚焦模型，改进后的公式可以提高数据的利用率，使重聚焦后的图像大小与范围与原图保持一致。在频域重聚焦中，改进后的公式将四维插值简化为二维插值，极大地降低了插值误差带来的影响，提高了计算效率。重聚焦实验表明，对于同一幅影像进行不同深度的重聚焦，空间域方法随着重聚焦次数增多耗费时间明显增多，而频域方法耗费时间增长慢。因此在实际应用中，如需对同一张影像进行多次重聚焦可以选取频域方法。通过实验验证了重聚焦的精度和效率主要取决于重采样插值方法。对于空间域而言，双线性插值一般可以达到较为优良的效果，并保持较快计算效率。对于频域而言，插值效率主要取决于插值半径，在基本消除伪像误差情况下，选择插值半径为2 像素具有较高效率。