基于气象资料的CRTSⅢ型无砟轨道温度场特性研究

2020-06-16周小勇曾小毛

铁道标准设计 2020年6期

周小勇,曾小毛,潘勋,倪林

(1.中国地质大学(武汉)工程学院,武汉 430074； 2.中铁十六局集团第三工程有限公司,浙江湖州 313000)

1 概述

随着我国高速铁路的发展，具有自主知识产权的CRTSⅢ无砟轨道得到广泛应用[1]。CRTSⅢ型无砟轨道由钢轨、扣件系统、预制轨道板、自密实混凝土层、隔离层及混凝土底座板等组成，其结构如图1所示。预制轨道板与自密实混凝土填充层通过板下预埋门式钢筋粘结成复合结构。底座板与上层结构通过土工布混凝土隔开。

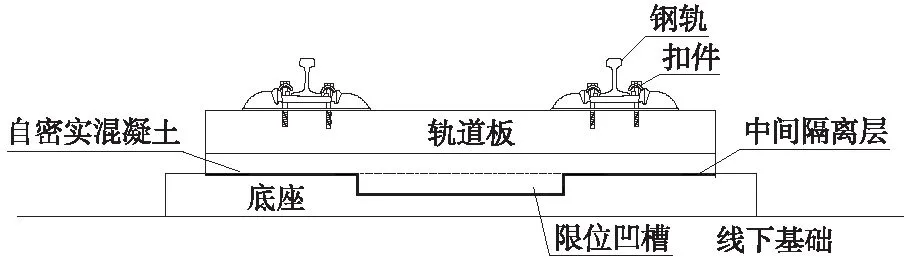
图1 CRTSⅢ型无砟轨道结构示意

高速铁路对轨道的平顺性提出了很高的要求。CRTSⅢ型无砟轨道板为混凝土结构，由于混凝土材料传热性能差，其内部温度较外界气温的变化具有明显的滞后性。轨道板表面升温时会出现“外热内冷”的状态，表面降温时轨道整体出现“外冷内热”的状态，从而使结构中产生较大的温度梯度。复合板结构受这种温度梯度影响会产生一定的翘曲变形[2，3]。受上下层结构约束，这种翘曲变形会使混凝土板中产生温度应力。当温度应力超过混凝土抗拉强度造成轨道结构层间离缝。此外，长期温度荷载作用下轨道板的翘曲变形将会增大，影响行车稳定性和安全性。因此，温度荷载是无砟轨道设计的主要荷载之一，影响轨道的强度和稳定性[4]。而不均匀的温度场是产生温度荷载的根本原因，开展无砟轨道温度场的研究对确定无砟轨道温度荷载具有重要意义。

国内外针对无砟轨道温度场特性的研究方法主要有两类：一类是基于传热学原理，借助气象资料求解热传导方程，得到轨道板结构温度场[5-9]；二是基于概率统计的方法，在轨道板内埋置温度传感器，通过实测数据的统计学分析建立板式无砟轨道温度的预测模型[10-13]。但传统研究多针对CRTSⅠ和CRTSⅡ型无砟轨道，针对CRTSⅢ型无砟轨道内部温度场特性的研究较少。现有的一些研究多针对具体轨道项目的实测数据进行分析，存在较大的局限性。为此，基于气象学原理研究CRTSⅢ型无砟轨道温度场特性，并通过实测数据验证模型正确性。此种方法不受地区气候限制，更具有实用性，可为CRTSⅢ型无砟轨道温度荷载取值提供参考。

2 传热学基本原理

无砟轨道结构温度场分析实质上是按照一定的初始条件和边界条件求解热传导方程。三维瞬态热传导方程的一般形式为[14]

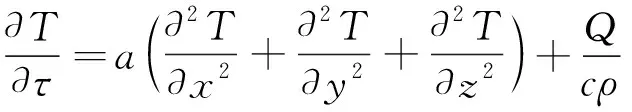
(1)

式中，a为导温系数，a=λ/cρ；λ为导热系数；c为混凝土比热容；ρ为混凝土密度；Q为单位时间单位体积混凝土内部发出的热量。一般研究无砟轨道施工后温度效应，此时结构内部水泥水化过程已完成，Q取0。

无砟轨道与外界环境主要通过太阳辐射、对流换热和辐射换热进行热交换。这3种换热形式主要与结构所处经纬度、日期、时刻、环境温度、风速、大气透明度系数和混凝土表面吸收率等气象因素有关[17]。在模型计算中常常将上述3种热交换作为边界条件施加在模型上。

由于ANSYS不能将太阳辐射热流密度和轨道板表面对流换热两种边界条件同时施加在结构表面，故将太阳辐射引起的热流密度换算到气温中。参考GB50176—2016《民用建筑热工设计规范》给出室外综合温度计算公式

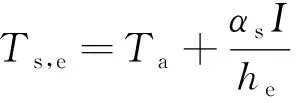
(2)

式中，Ts，e为轨道表面综合温度；Ta为轨道周围空气温度；I为结构外表面的太阳辐射强度，W/m2；αs为外表面的太阳辐射吸收系数；he为外表面换热系数，W/(m2·K)。

根据热传导原理，以气象数据建立无砟轨道边界条件，并通过实测数据验证该数值分析方法的准确性。在此基础上研究风速和日辐射强度对CRTSⅢ型无砟轨道温度场影响规律。

3 轨道结构模型

3.1 模型的建立

本文主要研究CRTSⅢ型轨道结构温度场变化规律，忽略钢轨、扣件、轨枕等的影响，采用ANSYS软件建立有限元分析模型。

CRTSⅢ型无砟轨道结构有限元模型如图2所示。轨道板、自密实混凝土层和底座均采用实体单元SOLID70进行模拟。考虑到轨道板与自密实混凝土层形成复合结构，层间通过绑定连接在一起。将太阳辐射引起的热流密度换算到气温中，得到综合温度。将其作为温度边界条件施加于结构表面，以实现对流荷载和热流密度荷载的同时施加。对流荷载施加在轨道结构顶面和侧面。

由于温度场的瞬态分析需要知道结构内部初始温度分布情况，在无实测数据的情况下很难获得结构内部初始温度分布情况。在正式分析前将前期数据进行迭代，可减少初始温度场影响[15-16]。因此，将正式分析前一天的计算结果作为初始温度场。

图2 CRTSⅢ型无砟轨道实体模型(单位：mm)

3.2 模型参数确定

采用传热学理论得到模型温度场，需要确定结构的基本参数包括：导热系数、比热容、密度，而进行应力分析时，则需给出结构的弹性模量、泊松比及线膨胀系数。目前尚无铁路相关规范给出无砟轨道的热工参数，依据钢筋混凝土的热工参数进行取值：导热系数为1.74 W/(m·K)，比热容为920 J/(kg·K)。混凝土表面的太阳辐射吸收系数与表面粗糙程度和颜色深浅有关，一般取值为0.6～0.65。轨道板表面光滑，为浅灰色，故取0.6[18-19]。

轨道板采用C60混凝土，自密实混凝土和底座板均采用C40混凝土，密度为2 500 kg/m3，泊松比取0.2，热膨胀系数为1×10-5/℃。

3.3 模型验证

为了验证所建立模型的有效性，将模型计算得到的温度与实测温度进行比较。在昌赣客专外泰和赣江特大桥施工工地附近建立了CRTSⅢ无砟轨道实尺模型，对轨道板温度场进行长期监测。监测时间从2018年10月开始，监测频率为2次/h，温度传感器布置如图3所示。

图3 无砟轨道温度传感器布置(单位：mm)

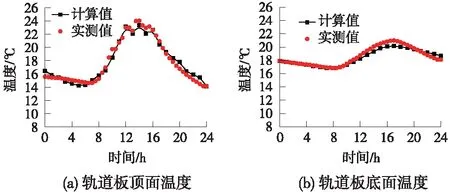
图4 轨道结构温度实测值与计算值对比

由图4可知，在无砟轨道表面施加11月份气象数据得到的温度荷载与实测轨道板底温度变化对比，其变化规律一致且数值差别不大。轨道板顶最大温度出现在下午14:00～15:00，模型计算最高温度为23.4 ℃，试验测试最大温度为24.0 ℃，与理论计算结果基本一致。计算值与实测轨道板顶温度峰值均出现在早上8:00左右，轨道板底面温度峰值在17:00左右，且计算值与实测值的最大误差为0.96 ℃，验证了本文中所建立的计算模型的可靠性。

4 轨道结构温度场分布规律

4.1 竖向温度分布规律

以12月19日温度场计算结果绘制典型时刻CRTSⅢ型无砟轨道结构温度随深度变化曲线，如图5所示。

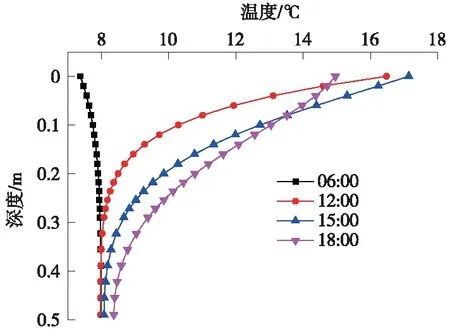
图5 温度沿竖向分布曲线

温度沿轨道结构竖向呈非线性分布，且随着深度的增加，温度变化幅度逐渐减小，当深度达到0.4 m时，竖向温度趋于一致。不同时刻内部温度梯度不同，早上6:00，结构内部呈现负温度梯度；受日照影响，12:00、15:00及18：00轨道结构上下层间出现正温度梯度。轨道结构正温度梯度近似为负温度梯度的1倍。

4.2 横向温度分布规律

轨道板不同时刻横向温度分布曲线及板中、板底、端部横向温度分布曲线如图6、图7所示。其温度分布存在以下特点：①不同时刻轨道板内温度横向分布不同，夜间气温较低，轨道结构以向外散热为主，导致表面温度低，内部温度则由于混凝土导热性能差而温度高，因此轨道夜间横向温度呈现中间高两边低；白天，轨道结构受日照影响，热量从板侧和板顶传入轨道结构内部，导致板侧表面温度高，中间温度低；②横向温度分布在靠近板边处为非线性，越靠近板边温度越高，至板中温度分布及数值几乎不变，在0.4～2.1 m存在温度平稳区；③受垂向温度场分布差异的影响，横向上轨道板板中及板底在温度平稳区数值上存在差异。

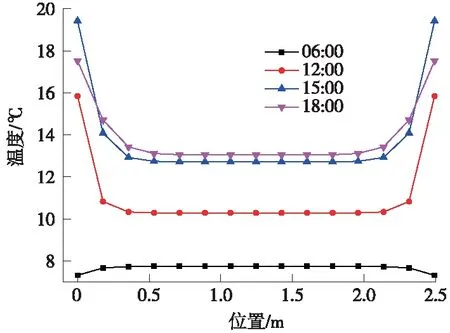
图6 不同时刻横向温度分布曲线

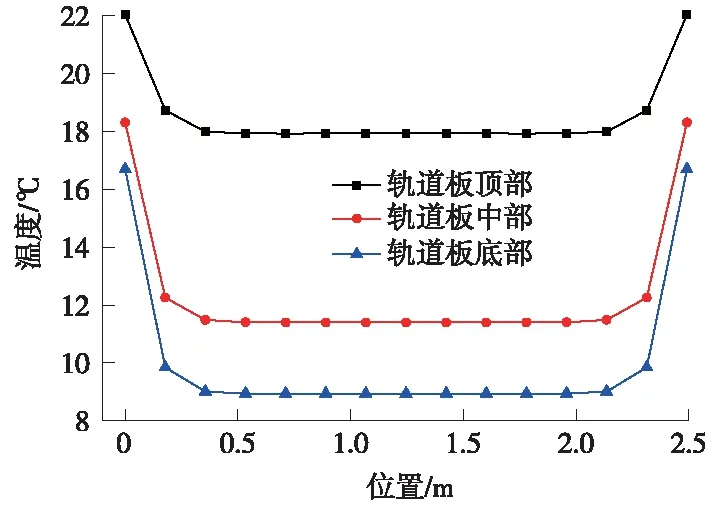
图7 不同位置横向温度分布曲线

5 太阳辐射强度及风速对轨道结构温度分布规律影响

5.1 太阳辐射强度对温度场影响

太阳辐射是轨道表面热量的主要来源，通过大气层到达地球表面，经过直接辐射、散射和反射传入轨道结构表面。式(2)给出的公式考虑了外界气温、太阳辐射强度及对流换热对轨道结构内部温度场变化的影响。太阳辐射强度以日为单位呈周期性变化，可从气象部门查询。2018年12月19日的太阳辐射强度变化曲线如图8所示。温度日变化曲线如图9所示。

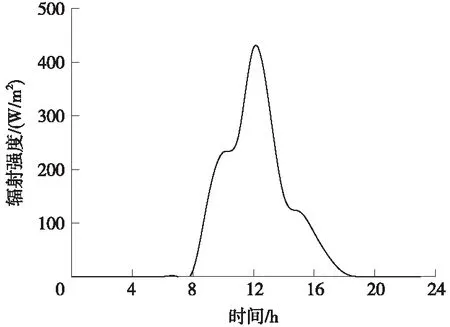
图8 太阳辐射强度日变化曲线(2018年12月19日)

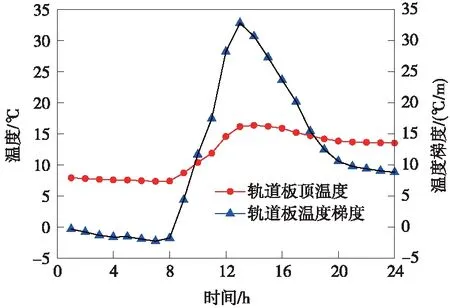
图9 温度日变化曲线(2018年12月19日)

由图8、图9可知，太阳辐射受季节影响较大，冬季白天时间短，辐射时间主要集中在8:00～18:00。太阳辐射强度最大出现在12:00，而轨道板顶最高温度和轨道板的温度梯度出现在13:00，存在明显滞后现象，滞后时间约1 h。由于混凝土导热性能差，轨道结构吸收外界热量速率较慢，导致表面升温滞后于太阳辐射强度。温度梯度变化规律与轨道板顶面温度变化规律基本一致，从负值到正值再到负值的循环变化，太阳辐射强度影响轨道结构正温度梯度。

5.2 风速对温度场影响

风速主要影响无砟轨道结构表面与空气的对流换热，在理论计算中表现为对流换热系数的影响。对流换热系数与表面形状、风速、周围空气温度等许多因素有关，可近似按照下式计算[20]

(3)

无砟轨道最不利温度梯度时的风速取值应为0 m/s，但考虑到无风条件与太阳辐射强度最大等极端气象条件同时出现的几率非常小。而且，混凝土与空气的表面对流换热系数是与风速直接相关的。因此，定量上来评估风速对无砟轨道梁温度场的影响是非常有必要的。取0，1，2，3级风速的平均值进行分析。采用式(3)计算得到相应的表面对流换热系数，见表1。取这些表面对流换热系数进行CRTSⅢ无砟轨道结构温度场的计算。不同风速下模型计算的轨道结构内部温度和温度梯度曲线如图10、图11所示。

表1 不同风速下的对流换热系数

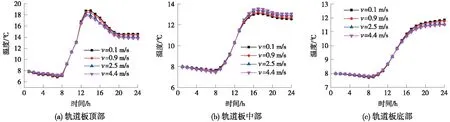
图10 不同风速下温度时程曲线

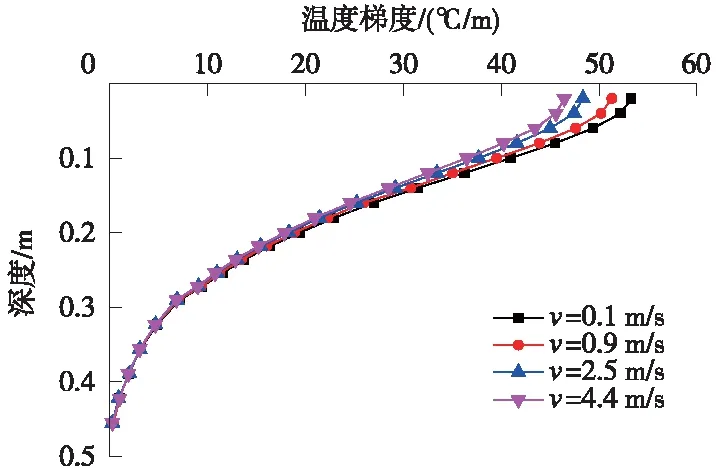
图11 不同风速下轨道结构竖向温度梯度曲线

由图10、图11可知，在自然对流(无风)、1级、2级、3级风力作用下，计算得出的轨道结构的最高温度分别为18.8，18.4，17.9，17.5 ℃。随着风速的增大，顶面区域的温度逐渐降低。风速对无砟轨道结构的温度梯度具有较大影响，其影响效应主要表现在接近轨道表面的位置，温度梯度最大差值为6.8 ℃。风速变化对轨道表面10 cm以内深度范围的温度梯度有明显影响，且深度越深，温度梯度随风速变化越小。10 cm以下范围的温度场受风速影响很小。轨道板以下自密实混凝土层及底座板几乎不受风速影响。