大规模MIMO系统中能效优化设计

张瑞清 李晖 宋选安 王天赐

摘  要： 能量效率是判断大规模多输入多输出（MIMO）技术是否符合绿色通信的重要指标之一。文中建立一种电路功耗模型，分析了多用户MIMO通信系统的能量效率问题。首先，建立多用户MIMO通信系统的下行链路传输模型和以发射功耗和电路功耗为主的功耗模型;其次，根据提出的系统模型得出系统能效的关系式;最后，提出一种改进的注水功率分配算法，以实现系统能量效率的最大化。仿真结果表明，在多用户MIMO通信系统中，系统总功耗会随着基站天线数目和小区内用户数目的增加而增加，而系统的能量效率并不会随着吞吐量无限增加，而是先递增达到最大值后下降。

关键词： 能效优化; 多输入多输出; 传输模型; 功耗; 能效分析; 功率分配

中图分类号： TN912?34                           文献标识码： A                        文章编号： 1004?373X（2020）07?0001?05

Energy efficiency optimization design in massive MIMO system

ZHANG Ruiqing1， 2， LI Hui1， 2， SONG Xuanan1， 2， WANG Tianci3

（1. School of Information Science and Technology， Hainan University， Haikou 570228， China;

2. Engineering Research Center of Marine Communication and Networks in Hainan Province， Haikou 570228， China;

3. Hainan Nuclear Power Co.， Ltd.， Changjiang 572733， China）

Abstract： Energy efficiency is one of the important indicators to judge whether the massive multiple input multiple output （MIMO） technology conforms to green communication. In this paper， a circuit power consumption model is established to analyze the energy efficiency of multi?user MIMO communication system. Firstly， the downlink transmission model and the power consumption model based on transmission power and circuit power consumption are established. Secondly， the relational expression of system energy efficiency is obtained by means of the system model proposed in this paper. An improved water?filling power allocation algorithm is proposed to maximize the energy efficiency of the system. The simulation results show that the total power consumption of the multi?user MIMO communication system increases with the increase of antennas in the base station and the users in the cell， and the energy efficiency of the system does not increase infinitely with increase of throughput， but increases first to the maximum and then decreases.

Keywords： energy efficiency optimization; MIMO; transmission model; power consumption; energy efficiency analysis; power allocation

0  引  言

随着无线通信技术的蓬勃发展，高速数据业务数量和种类呈现出爆发式增长的趋势，由此，信息与通信产业已经成为全球第五大耗能产业。作为第五代移动通信系统中的关键技术之一[1]，MIMO（Multiple Input Multiple Output）系统利用其超大规模天线阵列的优势，不仅扩大了系统的空间自由度，也提升了系统的频谱效率和能量效率。为了平衡日益增长的移动通信需求和降低通信系统能耗之间的关系，以达到绿色通信可持续发展的目的，研究以能量效率为导向的资源分配问题就显得十分重要[2]。

对于多用户的资源分配问题，传统的无线资源分配方案主要着眼于提升系统容量或者降低系统能量消耗，却较少考虑系统的能效问题。近年来，针对绿色通信系统中的能效优化资源分配问题开始成为研究热点。文献[3]在考虑了用户服务质量、能量发射功率、能量采集时间等因素下，建立了上行链路大规模MIMO系统，并提出均时最小QoS保证算法、吞吐量资源分配算法，提高了系统能效。文献[4]在多用户大规模MIMO移动通信系统的上行链路中，提出一种基于能效优化的资源分配算法，并联合了基站端的发射天线数和用户的发射功率来优化能效函数。文献[5]研究了关于多用户大规模MIMO系统的下行链路，主要说明了关于发射功率和天线数对系统能效的影响，借助Lambert W函数对系统天线数进行求解，提出一种低复杂度的天线选择算法，提高系统能效。文献[6]在大规模MIMO下行OFDMA（Orthogonal Frequency Division Multiple Access）系统中，采用迫零预编码方式接收信号，通过调整带宽分配、功率分配和基站天线数目分配的方式来优化能效函数。文献[7]利用张量平行因子（PARAFAC）分解的[k]?秩条件，通过迭代拟合的方法对能效函數中的收发端天线数目、编码长度等传输参数进行联合优化。文献[8]把多用户MIMO干扰信道的能效优化问题建模为一个非合作博弈问题，考虑了每个二级用户功率约束和干扰阈值，通过建立分布式迭代能效优化算法来获得纳什均衡。文献[9]基于多用户MISO（Multiple Input Single Output）系统，考虑了信干噪比、能量收集约束两个条件，提出一种拉格朗日函数结合Dinkelbach方法的资源分配方案，可以有效地提高系统能效。但是，这些研究未能在定量分析时更加充分地考虑系统约束情况下系统资源分配对大规模MIMO能效的影响。因此，设计能更加地满足用户服务质量要求的能效资源分配方案仍有待进一步完善。

基于对以上文献的整理及分析，本文针对多用户大规模MIMO系统下行链路场景，在综合考虑满足基站总发射功率和用户最低数据速率的条件下，假设发送端已知完全信道状态信息，以最大化系统能效为目标，提出一种基于改进的注水功率分配算法方案，可实现对系统资源的灵活调度，提升系统能效。

1  系统模型和问题描述

1.1  系统模型

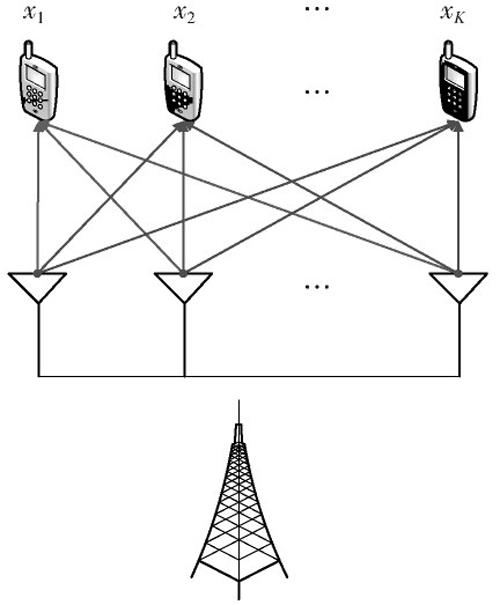
本文考虑建立一个典型的下行链路多用户MIMO无线通信系统，如图1所示。其中，在基站的位置配置[M]根发射天线，与单小区内的[K]个（[M≥K]）单天线移动用户进行通信，用户均匀分散在小区内部。

如果每个用户[k]（[k]=1，2，…，[K]）都可以获得完全的信道状态信息，那么用户在接收信号的同时也会受到来自其他用户的干扰和系统噪声，在用户接收端采用常用的信号接收方法消除用户间的干扰。在大规模MIMO下行链路中，用户[k]接收到的信号可以表示为：

式中：[y=y1，y2，…，yKT];[H=h1，h2，…，hKT]，表示[K×M]维信道矩阵，服从独立同分布的小尺度瑞利衰落;[F]是[M×K]维的线性预编码矩阵;[P=diagp1，p2，…，pK]表示分配给每个用户的功率;[x]表示[M×1]维的基站发射信号向量;[n]表示[K×1]维加性高斯白噪声（Additive White Gaussian Noise，AWGN），服从[n]～CN（0，1）。

1.2  问题描述

如图1所示，用户接收端接收到的信号包括有效信号、来自其他用户的干扰信号和信道环境中的噪声，用户[k]接收到的信号可以由式（1）得出：

[yk=pkhkfkxk+pii=1，i≠kKhkfixi+n] （2）

式中：[pkhkfkxk]是用戶[k]接收到的有效信号;[pii=1，i≠kKhkfixi]是来自其他用户的干扰信号;[n]是信道环境中的高斯白噪声。由此，可以得出用户的信噪比值[SINRk]为：

[SINRk=pkhkxk2pii=1，i≠kKhkxi2+σ2] （3）

现将用户[k]的数据速率表示为[Rk]，那么，在通信系统中用户的总速率[Rt]可以表示为：

[Rt=k=1KRk=Bk=1Klog2（1+SINRk）] （4）

将式（3）代入式（4）中，得：

[Rt=Bk=1Klog21+pkhkxk2pii=1，i≠kKhkxi2+σ2] （5）

式中：[B]表示系统的带宽;[σ2]表示系统的噪声功率[10]。系统中总功率的消耗主要体现在功率放大器消耗[PA]和其他的一些电路模块消耗[PC]。[PA]可以表示为：

[PA=Ptη] （6）

式中：[η]为功率放大器的效率;[Pt=k=1Kpk]是基站发射功率的总和。其他的电路模块中，消耗[PC]是不同元器件和数字信号处理所消耗的功率之和。电路功率消耗模型[11]可以表示为：

[PC=PFIX+PTC+PCE+PCID+PBH+PLP] （7）

式中：[PFIX]表示由冷却系统、信号控制和基带处理等信号处理过程所消耗的固定功率;[PTC]表示下行链路中传输过程中的功率消耗;[PCE]表示在信道估计时的功率消耗;[PCID]表示信道编码和信道解码的功率消耗;[PBH]表示数据传输回程中的功率消耗;[PLP]表示线性信号处理过程中的功率消耗。

系统的能量效率定义为系统的总平均和速率与系统总平均消耗功率之比，它的数学模型可以表示为：

[EE=RtPt=k=1KRkPA+PC] （8）

本文主要考虑基站天线数目[M]、小区内的用户数[K]等参数对系统能量效率的影响，并以系统能效最大化为优化目标进行求解。因此，可以将问题建模为：

[arg max EE= arg maxRtPt] （9）

[s.t.    C1： PA+PC≤Pmax，BS         C2： Rk≥Rmin] （10）

式中：约束条件[C1]是系统总发射功率的最大上限值;[C2]为用户[k]在进行数据传输中数据速率的要求。

2  基于功率分配的通信系统能效问题研究

2.1  注水功率分配算法

现用注水（Water?Filling，WF）算法给每个用户[k]分配相应的功率[12]，那么第[k]个用户分配到的功率可以表示为：

[pk=1gk-1μs.t.    C1： pk≥0         C2： pk≤Pmax，BS] （11）

式中：[gk]是第[k]个用户的有效信道增益;[μ]是注水的水位值。由此，式（3）可被重新表示为：

[SINRk=pkpkk=1Khkfk2+σ2] （12）

第[k]个用户可达到的速率可以表示为：

[Rk=Blog2（1+SINRk）] （13）

系统能效的表达式可以写为：

[EE=RsumPC+Kpk] （14）

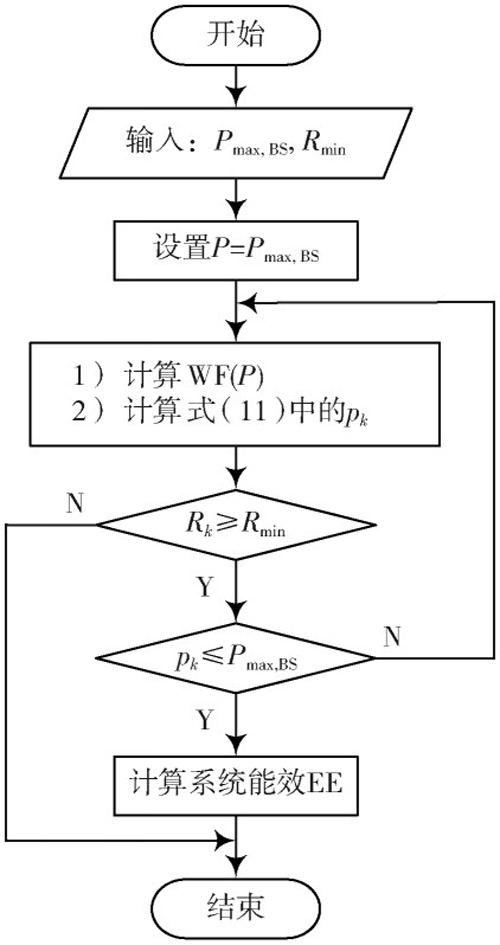
通过基于注水算法的功率分配来计算系统能效的流程图如图2所示。

2.2  基于改进的注水功率分配算法

在上述注水算法的基础上[12]，利用拉格朗日乘数法对算法进行改进，得到一种改进的注水功率分配算法。在下行链路中，基站发送给用户[k]的预编码矩阵权值可表示为：

[Sk=maxn=1，2，…，Nwnk2] （15）

因此，用户[k]的和速率可以表示为：

[maxk=1Kγklog2（1+gkpk）s.t.    k=1KpkSk≤Pmax，BS] （16）

根据式（16），构造拉格朗日函数：

[k=1Kγklog21+gkpk+μk=1KpkSk-Pmax，BS] （17）

因此，可以得到每个用户[k]被重新分配到的功率为：

[p?k=γk1+λB1+μKln2-KM-K] （18）

式中：[γk]的取值范围是0～1，代表每个用户[k]的优先级。对于所有用户[k]来说，当优先级相等时，[γk=1K]，这表明只有通过改变用户的优先级[γk]才能矫正改进注水算法的注水程度。那么系统能量效率的优化问题可以进一步表示为：

[EEkP=maxp?kk=1KRkp?kPts.t.    Rkp?k≥Rmin        k=1Kp?k≤Pmax，BS] （19）

基于上面提到的改进注水功率算法，则系统能效可以表示为：

[FP，λ，μ=k=1KRkp*k-EEkPPcx+k=1Kp*k+Puc+k=1KλRkp*k-Rmin-μk=1Kp*k-Pmax，BS] （20）

系统功率分配表示为：

[pEE=γk1+λBEEk+μKln2-KM-K] （21）

改进的注水功率分配算法计算系统能效的流程图如图3所示。

为了验证上述分析，利用Matlab平台进行实验仿真验证。在仿真中，考虑是单小区多用户大规模MIMO系统的下行链路模型的场景。假设仿真系统中的信道模型是小尺度多径瑞利衰落信道，带宽是20 MHz。系统的主要参数见表1。

图4主要说明了在不同的混合预编码模式下，单小区的下行链路的总电路功耗情况。图4中垂直轴的单位是dBm，选取用户数[K]的值为10，小区内基站天线数目[M]值的变化范围是10～600。从图4中可以看到，总电路功耗随着[M]值的增加而增加。其中，S?MMSE（Single?cell Minimum Mean Squared Error，单小区最小均方误差）预编码方式对系统中电路消耗的要求最高，其次是ZF（Zero Forcing，迫零）和MR（Maximal Ratio，最大比合并传输）预编码方式。当[M>]200时，三种预编码方式的差别变得更加明显，S?MMSE消耗的功耗明显增加。

在图5中，设置小区基站的天线数目[M]=100，让小区内的用户数目[K]从10～300变化。总电路功耗随着小区内用户数量的增加而增加，S?MMSE的预编码方式下消耗的能量是最多的，其次是ZF，MR预编码方式[13]，与图4中的结论类似。但不同的是，三种方式中，ZF的斜率最大，这说明用户数量对ZF预编码模式下的总电路功耗影响比较大。

图6中说明了S?MMSE预编码方式下系统吞吐量与系统能效之间的关系。小区基站天线数目[M]是15～300逐步递增，虚线代表[K]=10，实线代表[K]=35。当[K]=10和35时，系统能效分别为8.85 Mb?J-1?cell-1和8.82 Mb?J-1?cell-1，系统的吞吐量分别是456.16 Mb?s-1?cell-1和833.98 Mb?s-1?cell-1。通过对比，可以看出增加天线数目可以提高系统的吞吐量，但不一定可以提高系统的能量效率。

图7和图8分别是ZF，MR预编码方式下的系统吞吐量与系统能效之间的关系图。与S?MMSE预编码方式下关系图的大概走向一致，因此，可以得出结论：预编码方式的不同对吞吐量和系统能效之间关系的影响不大。图6～图8中曲线在最大系统能效EE（Energy Efficiency，能量效率）點附近相对平滑，说明当把系统吞吐量和系统能效EE提高到最大的EE点时，如果一味地追求高吞吐量，那么将会带来系统能效的损失[14]。

4  结  语

本文对多用户MIMO通信系统中下行链路的能效问题进行研究，在满足用户质量的情况下，对能效资源进行合理的分配。仿真说明了在多用户MIMO通信系统中系统总功耗会随着基站天线数目和小区内用户数目的增加而增加;系统的能量效率并不会随着吞吐量无限增加，而是先递增达到最大值后下降。

接下来的研究可以通过设置不同的（[M]，[K]）组合在相同的仿真环境下进行实验，得出一个小区基站天线数目[M]和用户[K]的一个比例关系，在此条件下，系统能量效率基本稳定在一个值附近。这会对实际生活中小区布置基站时提供一个合理的天线比例，在一定程度上可以减少资源的浪费。

注：本文通讯作者为李晖。

参考文献

[1] BOCCARDI F， HEATH R W， LOZANO A， et al. Five disruptive technology directions for 5G [J]. IEEE communications magazine， 2013， 52（2）： 74?80.

[2] 王茜竹，邱聪聪，黄德玲.面向5G的大规模MIMO关键技术研究分析[J].电子技术应用，2017，43（7）：24?27.

[3] 万晓榆，魏霄，王正强，等.基于能量采集的大规模MIMO系统能效优化[J].计算机应用研究，2019（4）：1?3.

[4] 胡莹，黄永明，俞菲，等.多用户大规模MIMO系统能效资源分配算法[J].电子与信息学报，2015，37（9）：2198?2203.

[5] 刘紫燕，刘世美，唐虎，等.多用户Massive MIMO系统能效资源分配方案[J].中国科技论文，2018，13（14）：1658?1663.

[6] 胡莹，冀保峰，黄永明，等.大规模MIMO OFDMA下行系统能效资源分配算法[J].通信学报，2015，36（7）：40?47.

[7] 刘亚丽，李双志，段海鹏，等.面向能效优化的MIMO系统参数配置[J].电讯技术，2017，57（9）：1035?1040.

[8] HAN Shujun， LU Yanhui， YANG Shouyi， et al. Game theory?based energy efficiency optimization in multi?user cognitive MIMO interference channel [C]// 2016 IEEE MTT?S International Wireless Symposium （IWS）. Shanghai， China： IEEE， 2016： 1?4.

[9] CHEN P， SHI Q， XU W， et al. Energy efficiency optimization for multi?user MISO SWIPT systems [C]// IEEE China Summit and International Conference on Signal and Information Proces?sing. Chengdu， China： IEEE， 2015： 772?776.

[10] TAN Weiqiang， JIN Shi， YUAN Jide. Spectral and energy efficiency of downlink MU?MIMO systems with MRT [J]. China communications， 2017（5）： 105?112.

[11] BJORNSON E， SANGUINETTI L， HOYDIS J， et al. Optimal design of energy?efficient multi?user MIMO systems： is massive MIMO the answer？ [J]. IEEE transactions on wireless communications， 2015， 14（6）： 3059?3075.

[12] GUO K， GUO Y， ASCHEID G. Security?constrained power allocation in MU?massive?MIMO with distributed antennas [J].IEEE transactions on wireless communications， 2016， 15（12）： 8139?8153.

[13] MOHAMMED S K. Impact of transceiver power consumption on the energy efficiency of zero?forcing detector in massive MIMO systems [J]. IEEE transactions on communications， 2014， 62（11）： 3874?3890.

[14] LIU W， HAN S， YANG C. Energy efficiency scaling law of massive MIMO systems [J]. IEEE transactions on communications， 2017， 65（1）： 107?121.