大规模MIMO系统中低复杂度信号检测算法
2020-06-15任茜源郑兴林
任茜源,郑兴林
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
大规模多输入多输出(Multiple-Input Multiple-Output, MIMO)技术由于其高频谱利用率成为第五代(5G)移动通信系统中的关键技术[1]。在上行链路中,最优最大似然(Maximum Likelihood,ML)检测算法[2]的计算复杂度随着用户天线数和调制阶数的增加呈指数增长,难以在大规模MIMO系统中实现;传统的线性检测算法因涉及高维矩阵运算,其计算复杂度较高[3]。近年来,研究者提出了一些次优的非线性检测算法,其中,基于因子图的置信度传播(Belief Propagation,BP)算法[4]有较低的计算复杂度,但因子图的全连接结构导致BP算法存在环路效应[5-6];文献[7]提出了近似消息传递(Approximate Message Passing,AMP)算法,其传递过程只需传递均值和方差,从而降低了计算复杂度;在AMP算法的基础上,文献[8]利用信道硬化现象提出了消息传递检测(Message Passing Detection,MPD)算法;文献[9]基于MPD算法选择部分符号概率计算每次迭代过程中传递的消息,从而得到低复杂度的概率近似-消息传递检测(Probability Approximation-MPD, PA-MDP)算法[9-10]。但MPD和PA-MPD算法的复杂度也会随天线数及调制阶数的增加而增大,同样难以运用于高阶调制系统[11]。
本文在MPD算法基础上,利用更新部分符号概率的策略,提出了一种选择性更新-消息传递检测(Selective Update-MPD,SU-MPD)算法。仿真结果表明,与MPD和PA-MPD算法相比,改进算法在保证检测性能的同时,可有效降低计算复杂度。
1 大规模MIMO系统模型及信道硬化特性
1.1 系统模型
在多用户的大规模MIMO系统中,设有K个单天线用户,基站端具有N(N>K)根接收天线。系统模型为
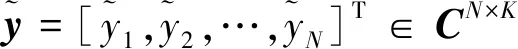
1.2 信道硬化特性
信道硬化指MIMO信道的互信息方差相对于其均值增长非常缓慢或随着天线数量的增加而缩小的现象[12]。信道硬化特性给大规模MIMO系统的信号处理带来很多优势。其中,随着信道尺寸的增加,HTH矩阵非对角线元素的值与主对角线元素的值相比变得越来越小。MPD检测算法利用该特性实现大规模MIMO系统的低复杂度和高性能信号检测。
2 MPD算法
2.1 MPD算法
MPD算法[8]分为消息传递和HTH估计。将式(1)两端同乘HT后改写为


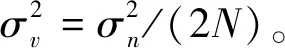

在MPD算法的信道估计中,假设Xp=PI2K是幅度为P的导频矩阵,I2K为单位矩阵,接收端收到的导频信号为

2.2 PA-MPD检测算法

3 改进的MPD算法

迭代过程结束后,根据星座点集合中最大符号概率pj(sk)判断发送符号sk。
综合上述算法,得到SU-MPD算法如下:
Output:L
2: fort=1 do
3: fori=1 to 2Kdo





9:Ai=sort(pi)
10: end
11:end
12:fort=2 to number_of_iterations do
13: fori=1 to 2Kdo
14:M←according to the range of values of
max (pi)





20:Ai=sort (pi)
21: end
22:end
其中,Δ为衰减因子;t为迭代过程提前终止的阈值,当最大的符号概率值>t时,终止算法的迭代过程。
4 性能与复杂度分析
4.1 仿真性能分析
本小节中,我们将在不同天线配置和调制方式下,通过大量仿真选取SU-MPD算法终止迭代的符号概率阈值T。当T=1时,SU-MPD与PA-MPD算法的消息迭代更新过程相同,具有最大的计算复杂度。SU-MPD算法的计算复杂度随T的减小而减小,但同时SU-MPD算法的性能也存在一定的损失。因此,在不影响SU-MPD算法检测性能的情况下,折衷选取最优符号概率阈值T=0.9,可有效降低算法的计算复杂度。不同调制方式下的更新符号数为Q。
在对比分析改进的SU-MPD算法与PA-MPD和MPD算法的误码率(Bit Error Rations, BER)性能时,SU-MPD算法与MPD及PA-MPD算法采用相同的迭代次数,即16QAM、64QAM和256QAM调制的信号检测算法的迭代次数分别为7、13和13。表1为SU-MPD算法在3种调制方式和不同发送天线数配置下,基于符号概率消息传递所需更新的点数Q。16QAM和64QAM调制方式下,根据最大符号概率值选取1个或2个符号概率更新点数;在256QAM的高阶调制方式下,为了保证算法的检测性能,将符号概率更新点数Q增加为2或4。

表1 不同调制方式下符号概率更新数Q的取值
图1对比了调制方式为16QAM、单天线用户数K=8时,不同接收天线数N随着信噪比(Signal

图1 16QAM调制方式、K=8时,3种算法的性能对比
Noise Ratio,SNR)的增加对3种算法BER性能的影响。由图可知,N=32和64时,与MPD和PA-MPD算法相比,SU-MPD算法的检测性能有较小的损失。当N=128时,SU-MPD、MPD和PA-MPD算法BER曲线几乎完全重合。随着接收天线数的增加,SU-MPD算法检测性能趋近于PA-MPD算法检测性能。不同N对应的SU-MPD方案计算复杂度将在下一小节分析。
图2和3所示为大规模MIMO系统中接收天线数N=128、单天线用户数K=8、16、32和不同调制方式下SU-MPD、MPD和PA-MPD算法的检测性能。

图2 16QAM调制方式、N=128时,3种算法的性能对比

图3 256QAM调制方式、N=128时,3种算法的性能对比
由图2和3分析可知,两种调制方式下,K=8和16时,SU-MPD算法的检测性能与PA-MPD和 MPD算法的检测性能趋于一致。当K=32时,与MPD算法相比,SU-MPD算法的检测性能有较小的损失。
调制方式为16QAM时(如图1所示),在BER=10-5时SU-MPD算法的检测性能略低于MPD算法,而与 PA-MPD算法检测性能一致。调制方式为16QAM的BER曲线如图2所示,与MPD算法相比,在BER=10-4时SU-MPD算法的检测性能损失了0.2 dB,PA-MPD与 MPD算法检测性能相当;由图3可知,在16QAM符号概率更新点数的基础上,可以通过增加更新点数来保证SU-MPD算法在256QAM调制方式下的检测性能,且使得SU-MPD算法检测性能优于PA-MPD算法。由此可知,在当前终止迭代的符号概率阈值T和更新符号概率点数Q下,用户天线数和调制阶数较大时,SU-MPD算法的检测性能更接近MPD算法。
4.2 计算复杂度分析
由于SU-MPD算法的计算复杂度随着SNR的增大而减小,因此仿真可通过统计每个SNR下SU-MPD算法迭代过程中平均更新的概率点数来衡量改进算法的计算复杂度。
图4所示为在16QAM调制方式和单天线用户K=8的配置下,SU-MPD算法相对于MPD和PA-MPD算法的计算复杂度比值曲线。由图可知,当接收天线数N=32时,SU-MPD与MPD和PA-MPD算法的计算复杂度比值随着SNR的增大而趋于定值:35%及65%。且当N值增加时,计算复杂度比值变小,这表明通过更新部分符号概率能有效降低计算复杂度。

图4 16QAM调制方式、K=8时,不同N下SU-MPD与MPD及PA-MPD算法复杂度比值
图5和6分别表示调制方式为16QAM和256QAM、K=8、16和32时,SU-MPD与MPD算法及SU-MPD与PA-MPD算法计算复杂度的比值曲线。由图可知,K值较小时改进算法的计算复杂度降低趋势更为明显,且SU-MPD算法计算复杂度最大限度能降低为MPD算法计算复杂度的19%,PA-MPD算法计算复杂度的55%。
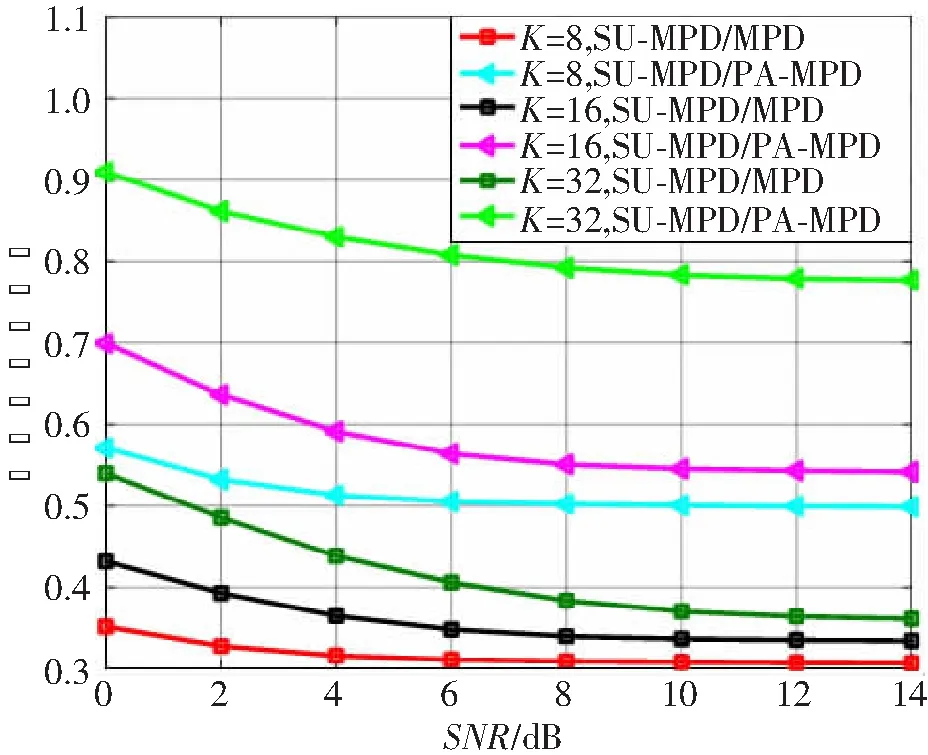
图5 16QAM调制方式、N=128时,SU-MPD与MPD及PA-MPD算法复杂度比值
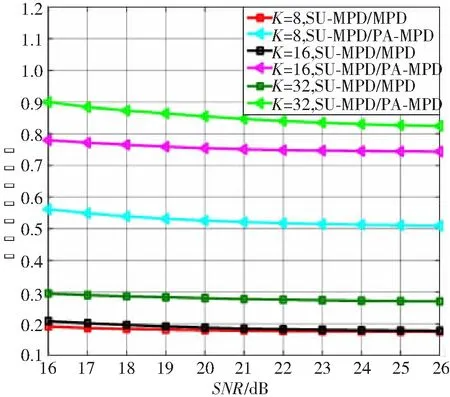
图6 256QAM调制方式、N=128时,SU-MPD与MPD及PA-MPD算法复杂度比值
表2所示为在调制方式为256QAM、SNR=26时,SU-MPD、MPD和PA-MPD算法的计算复杂度比较(用加法和乘法运算次数体现)。

表2 3种检测算法的加法和乘法运算次数
通过上述计算复杂度分析可知,在保证信号检测性能的前提下,改进的SU-MPD算法与PA-MPD及MPD算法相比可以有效地降低计算复杂度,更能适用于大规模MIMO高阶调制系统。
5 结束语
本文在MPD算法的基础上,基于符号概率引入提前终止迭代过程和更新部分符号概率的策略,提出了SU-MPD算法。仿真结果表明,SU-MPD算法能显著降低计算复杂度,且SU-MPD算法的检测性能与PA-MPD算法及MPD算法性能趋于一致。
