不同随机场模拟对斜坡失稳风险评估结果的影响
2020-06-15李丞苏立君
李丞,苏立君,3
(1.中国科学院 山地灾害与地表过程重点实验室;中国科学院、水利部 成都山地灾害与环境研究所,成都 610041; 2.中国科学院大学,北京100049;3.中国科学院 青藏高原地球科学卓越创新中心,北京100101)
已有研究表明[1-3],土体参数空间变异性对斜坡稳定性影响显著。通常,斜坡滑动面倾向于寻找最不利的失稳路径,这些滑动面不仅存在一定的空间变异性,而且相互之间具有相关性,因此,斜坡存在多种滑动面形式[1-2]。从工程角度来看,不仅要考虑斜坡的稳定性,还应考虑斜坡的失稳后果,若不考虑滑动面间相关性的影响,就会高估斜坡的失稳风险[3]。近年来,斜坡失稳风险评价受到了较多的关注。Li等[4]将子集模拟算法引入随机有限元算法,为小概率水平下的斜坡失稳风险计算提供了一种有效方法。Li等[5]提出一种基于具有代表性滑动面的极限平衡法,可为边坡失稳风险提供定量评价。Xiao等[6]提出辅助随机有限元法,使得随机有限元算法在三维斜坡风险评估中得到应用。Jiang等[7]在极限平衡分析框架下,提出一种考虑土体二维空间变异性的边坡失稳风险定量评估方法。
上述研究中,均采用平稳随机场模型来描述土体性质的空间变异性[8],然而,土体受沉积条件、地质和环境等作用影响,导致相应的土体参数呈现沿埋深变化的趋势[9]。值得注意的是,目前,已有学者[10-13]认识到土体参数非平稳分布特征对斜坡概率分析的影响。由文献[10-13]可知,文献[4-7]高估了斜坡失稳概率,因此,在评价斜坡失稳风险时需考虑土体抗剪强度参数的非平稳分布特征。
学者们很少关注使用非平稳随机场表征土体抗剪强度参数来评价斜坡失稳风险。针对这一问题,笔者采用随机场模拟土体抗剪强度参数分布特征,结合有限元极限分析法、强度折减法和Monte Carlo模拟来计算斜坡安全系数和失效概率,并讨论了使用非平稳随机场和平稳随机场模拟土体抗剪强度参数分布特征的差异对斜坡失稳风险的影响。
1 不排水抗剪强度参数非平稳随机场模拟
土体参数的空间变异性由趋势参数和随机波动参数组成,不同深度处的土体参数ξ(d)可表示为[9]
ξ(d)=t(d)+w(d)
(1)
式中:d为地面以下土体深度;t(d)为趋势参数函数,即土体参数在埋深d处的均值;w(d)为随机波动参数函数,w(d)为均值和标准差不随深度变化的统计平稳随机场[9]。t(d)与土体物质组成、沉积条件和固结过程等有关[14]。对于正常固结粘土层,t(d)从地表处沿深度增加(起始值为0);对于高度超固结粘土层,t(d)沿深度不发生变化;对于土层较厚的超固结粘土层,t(d)从地表处沿深度增加(起始值为某固定值)。尽管土体参数沿深度方向可能存在非线性变化的趋势,为简单起见,t(d)一般选择简单的线性函数[15]。为此,只研究超固结粘土层趋势参数函数从地表处沿深度增加的情况。据此,土体不排水抗剪强度参数cu由某一定值cu0随深度增加的表达式为[11,13]
cu(d)=cu0+ρσv=cu0+ργd
(2)
式中:cu0为地面处土体的不排水抗剪强度,kPa;ρ为土体不排水抗剪强度随深度增加的速率,kPa/m;σv为垂直有效应力,kPa,σv=γd;γ为土体重度,kN/m3,d为地面以下土体深度,m。采用文献[11,13]的方法,模拟土体不排水抗剪强度的非平稳分布特征:首先,将cu0模拟为均值为μcu0和标准差为σcu0的对数正态平稳随机场,然后,考虑cu随深度线性变化的影响,就此得到cu的二维非平稳随机场为
(3)
根据式(3),得cu的均值和标准差分别为
μcu=μcu+ργd
σcu(d)=COVcu0(μcu0+ργd)
(4)
模拟随机场的数据为土体参数的均值、方差以及方差折减函数,而方差折减函数取决于相关函数及相关距离。方差折减函数用于描述空间平均后的方差和点方差的关系,如式(5)所示。
(5)
式中:D为平均间距;ρ(θ)为相关函数,可由协方差函数求得。Li等[16]研究了不同相关函数对边坡可靠度的影响,发现相关函数对可靠度影响不大,因此,选用形式简单的指数型相关函数
(6)
式中:x1、x2、y1、y2是随机场域内的坐标;lh和lv分别表示水平和竖直相关距离。通过Karhunen-Loeve级数展开法[17]生成随机场。
2 斜坡安全系数计算和失稳风险评估方法
采用有限元极限分析下限法进行斜坡稳定性计算。有限元极限分析下限法指出:在任何静力许可应力场内可以计算真实极限荷载的下限值(或“安全值”)。静力许可应力场需满足平衡条件、应力边界条件和屈服条件(应力必须位于应力空间的屈服面内部或之上)。下限解是求解满足静力许可条件的最大破坏荷载[18]。
使用强度折减法,计算边坡安全系数[18]
(7)
图1给出了有限元极限分析下限法的斜坡安全系数分析流程[18]。TOL为收敛精度,文中取0.001。
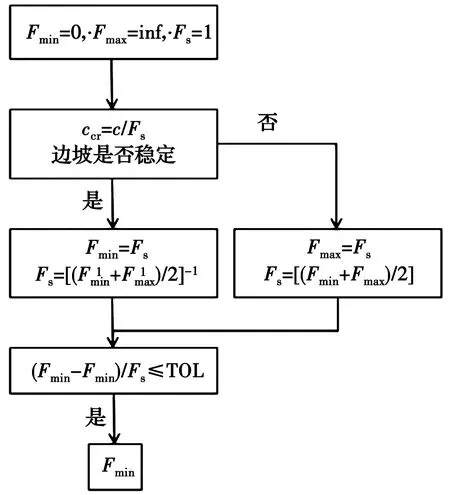
图1 有限元极限分析下限解的斜坡安全系数分析流程Fig.1 Analysis flow of lower limit solution of finite element limit analysis of slope safety factor
在强度折减过程中,采用K聚类方法(K-means clustering method)[17]搜索滑面的形状和位置,据此滑面计算滑坡体积。
斜坡每一次计算都会生成一个安全系数。对于一系列随机场实现,使用Monte Carlo方法可获得全部安全系数,Monte Carlo方法的具体思路如图2所示。因此,Monte Carlo方法被用于产生足够数量的不排水抗剪强度随机场,并进行斜坡稳定性分析。
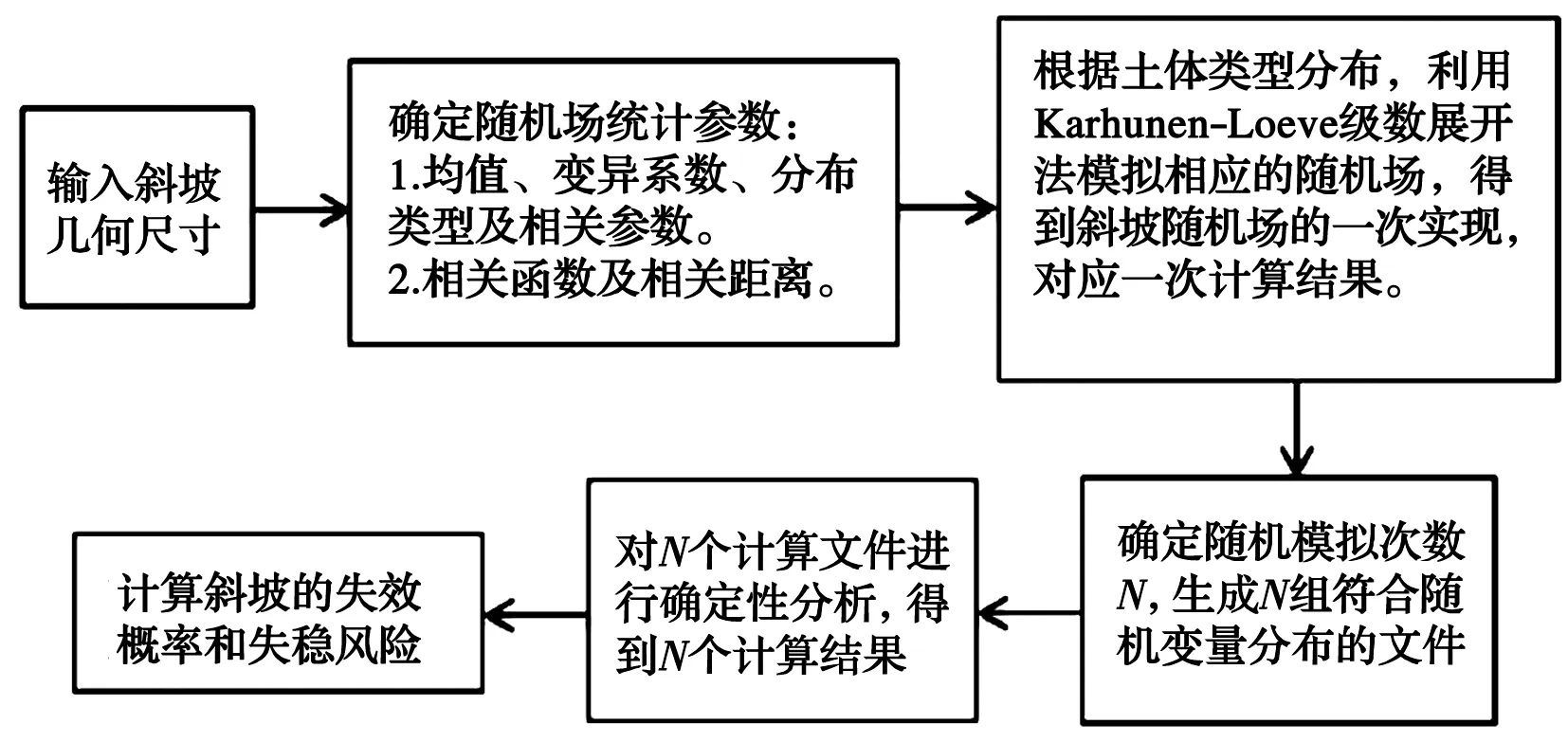
图2 利用Monte Carlo模拟计算斜坡失效概率和失效风险 的流程图Fig.2 The flow chart of calculating slope failure probability and failure risk by Monte Carlo simulation
用式(8)计算斜坡失效概率。
(8)

在得到斜坡失效概率及失效后果后,斜坡失稳风险R可以被评价为
R=C×Pf
(9)
式中:C为斜坡失稳后的量化结果[17]。式(9)仅适用于斜坡滑动面形式唯一时的情况。然而,在评价空间变异性的斜坡中可能存在多种滑动面形式,所以,每种斜坡滑动面形式相关的后果都应该单独评估,于是,采用文献[17,19]中的公式评估斜坡失稳风险。
(10)

3 算例分析
3.1 土体不排水强度参数随机场模拟
以文献[13]的一个不排水饱和粘土斜坡为例进行分析,如图3所示。根据文献[13]可知,斜坡高度10 m,坡比为1∶2,土体重度γ=20 kN/m3。
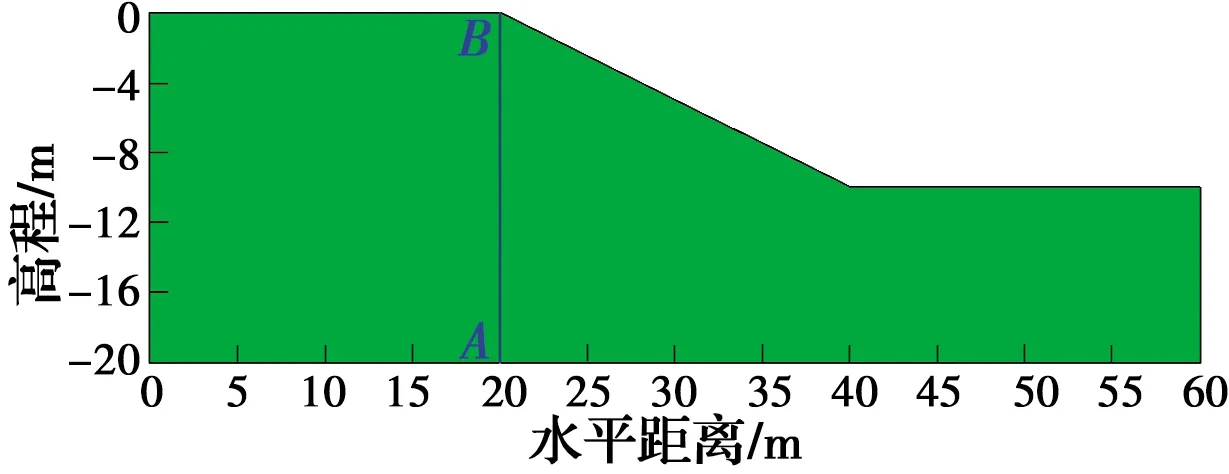
图3 不排水饱和粘土斜坡Fig.3 The undrained saturated clay slope
斜坡模型划分为1 000个三角形单元,Monte Carlo模拟次数在计算结果满足精度的条件下,计算次数为1 000次。为描述cu沿深度方向的非平稳分布特征,即cu均值和标准差随埋深的增加而增大的特性,将cu模拟为μcu0=14.669 kPa和σcu0=4.034 kPa的对数正态平稳随机场,水平相关距离δh=19 m,竖直相关距离δv=1.9 m,参数ρ为0.15,变异系数为25%。同时,为了比较采用非平稳随机场和平稳随机场模拟土体抗剪强度参数空间变异性的差异对斜坡可靠度和失稳风险的影响,参照文献[10,20]的做法,取斜坡中部(z=-10 m)处的不排水强度均值和变异系数分别为44.67 kPa和27.5%,模拟对应的cu对数正态平稳随机场实现值,也取δh=19 m和δv=1.9 m。
为了便于说明,定义使用非平稳随机场模拟土体抗剪强度参数时为工况1,使用平稳随机场模拟土体抗剪强度参数时为工况2。图4和图5给出了cu(x,d)沿深度方向(图3中的AB截面)的3次典型实现值。由图4可知,工况1的cu均值随着埋深的增加而增大,通过分析cu典型实现值沿埋深方向的变化趋势可知,σcu同样沿埋深增加,说明此模型能够模拟cu的非平稳分布特征。由图5可知,工况2由于没有考虑趋势分量的影响[11],cu值的大小与深度没有关系,其相应的cu典型实现值呈现杂乱无章的变化,导致土体内部随机场实现值变化较大。此外,由工况1获得的随机场实现值,大多分布在cu均值的右侧,由工况2获得的随机场实现值在cu均值两侧较均匀的波动。
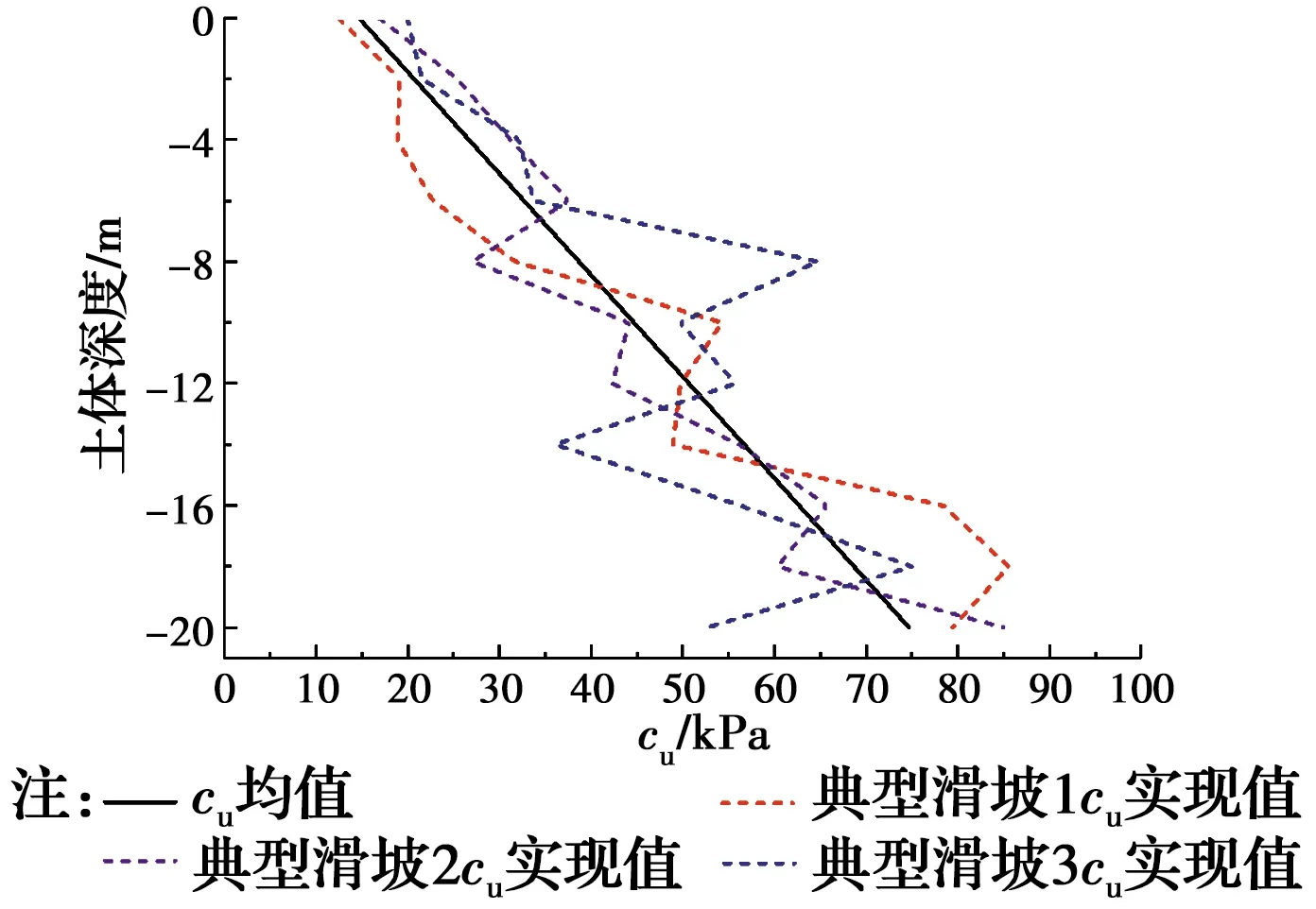
图4 工况1的不同cu实现值Fig.4 Different cu for condition 1

图5 工况2的不同cu实现值Fig.5 Different cu for condition 2
将工况1和工况2获得的二维非平稳随机场和二维平稳随机场cu(x,d)典型实现值分别赋予给斜坡模型,如图6和图7所示。由图6和图7可知,红色部分为cu值较大区域,蓝色部分为cu值较小区域。此外,土性参数空间变异性导致多种滑动面形式,滑动面位置和形状及其安全系数均发生明显变化,即:斜坡安全系数与滑动面位置和形状没有直接联系。
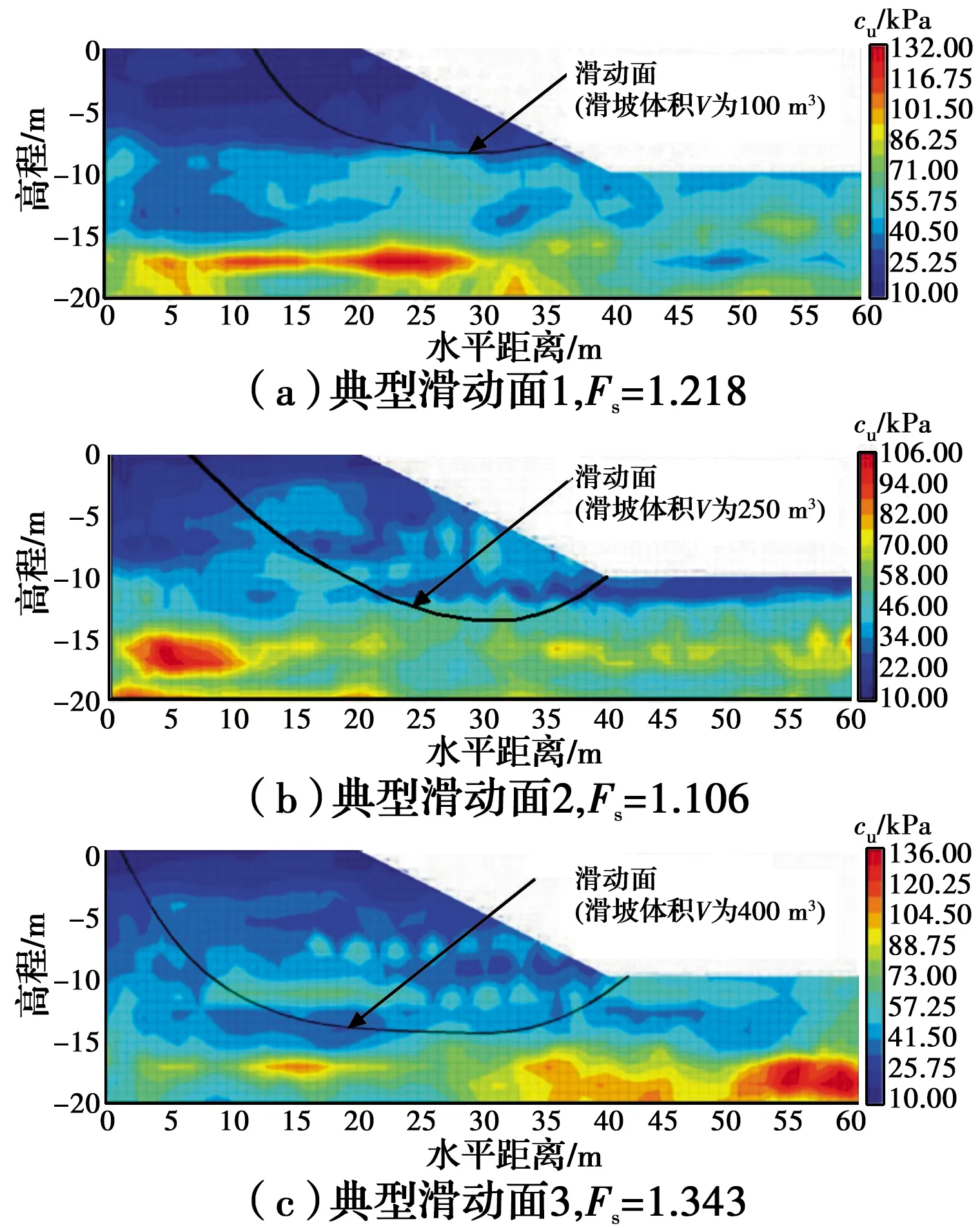
图6 工况1某次典型实现值及滑动面形式Fig.6 A typical realization value and failure mode for condition 1

图7 工况2某次典型实现值及滑动面形式Fig.7 A typical realization value and failure mode for condition 2
3.2 斜坡可靠度分析和失稳风险定量评估
获得cu随机场实现值后进行斜坡可靠度分析与失稳风险定量评估。采用Monte Carlo进行非平稳随机场和平稳随机场斜坡可靠度计算得到的Pf分别为0.044和0.062,与文献[13]计算的非平稳随机场Pf=0.044 1基本一致,而且采用非平稳随机场计算得到的Pf小于采用平稳随机场计算得到的Pf,这与文献[20-21]得出的结论吻合。工况1和工况2情况下混合滑动体积的直方图如图8和图9所示。从图8和图9可知,当考虑土体抗剪强度参数非平稳分布特征时,斜坡滑动体积的峰值约在250 m3左右,而不考虑土体抗剪强度参数非平稳分布特征时,斜坡滑动体积的峰值约在750 m3左右。
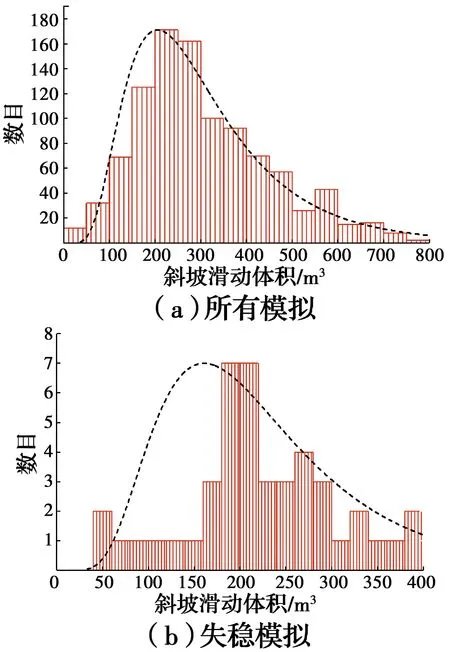
图8 工况1混合滑动体积直方图Fig.8 Mixed sliding volume histogram for condition 1
浅层滑动面位置和深层滑动面位置的定义如文献[17]所述,本文不再描述。不同工况下斜坡发生不同滑动面位置的直方图如图10和图11所示,从图10和图11可知,深层滑动面是主要的滑动面形式,在工况2情况下,深层滑动面的比例远大于工况1。工况1和工况2的斜坡失稳风险分别为9.8、35.69 m3。
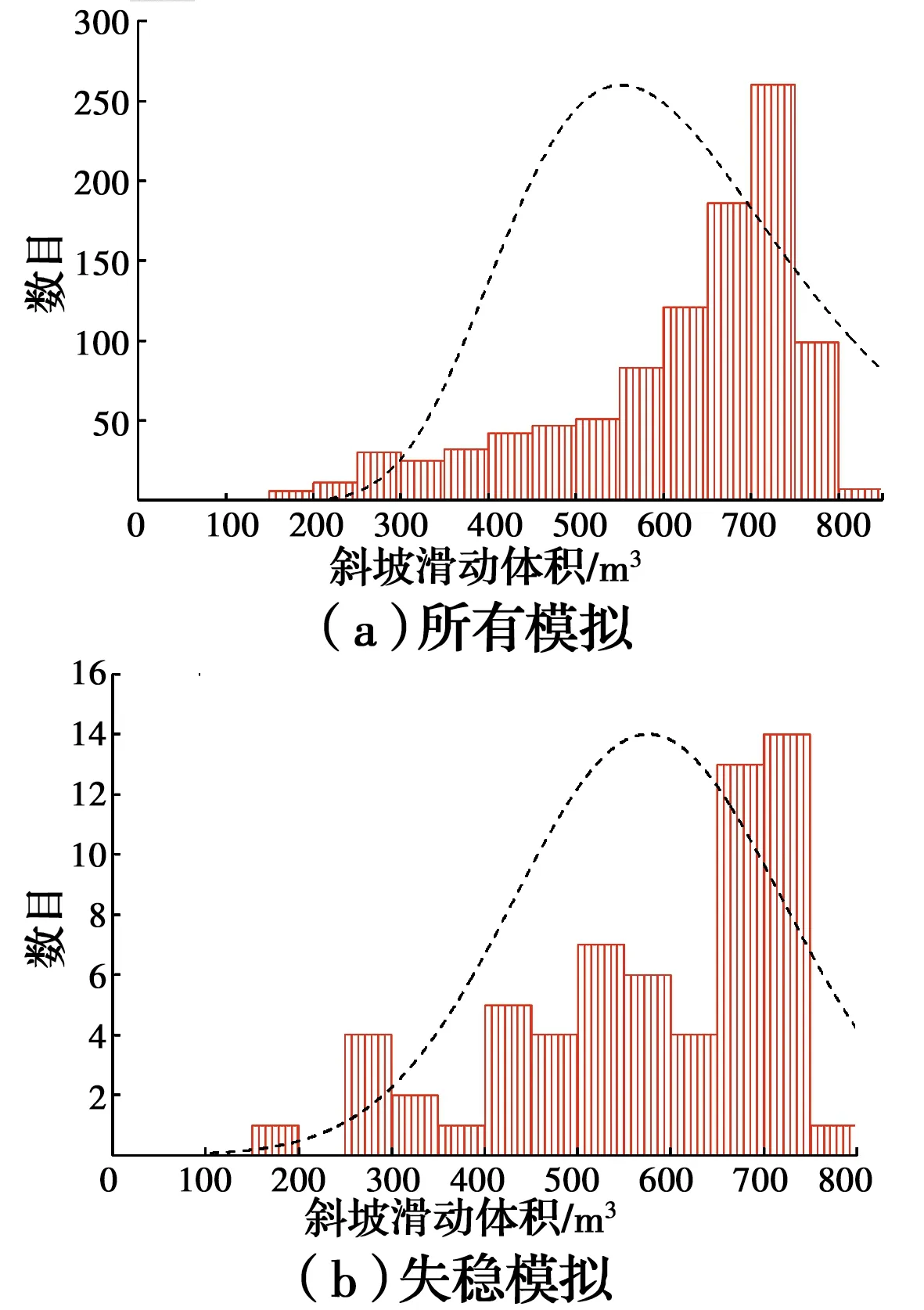
图9 工况2混合滑动体积直方图Fig.9 Mixed sliding volume histogram condition 2

图10 工况1分解滑动体积直方图Fig.10 Decomposition sliding volume histogram for condition 1
3.3 空间变异性对失效概率和失稳风险的影响


图11 工况2分解滑动体积直方图Fig.11 Decomposition sliding volume histogram for condition 2

图12 竖直相关距离对失效概率和失稳风险的影响Fig.12 Effectofvertical correlation distance on failure probability and failure risk

图13 竖直相关距离对滑动面形式的影响Fig.13 Effectofvertical correlation distance on sliding surface types
4 结论
结合有限元极限分析、强度折减法和蒙特卡洛模拟,比较了使用非平稳随机场模型和平稳随机场模型对计算斜坡失稳风险和滑动面位置和形状的影响,得到以下结论:
1)当土体参数存在空间变异性时,仅由斜坡安全系数是无法准确评价滑坡体积大小和位置及所产生的失稳风险,故需与具体滑动面形式及滑坡体积结合,进行滑坡风险综合分析。
2)采用平稳随机场计算得到的斜坡深层滑动面的数量远远大于采用非平稳随机场。
3)斜坡竖向空间变异性对采用非平稳随机场计算其失稳风险的影响较小,对失效概率的影响较大,相比之下,斜坡竖向空间变异性对采用平稳随机场计算其失稳风险和失效概率的影响显著。
4)在边坡稳定性理论分析中(如极限分析法和极限平衡法),需预先设定滑动面位置和形状。在这种情况下,精确的滑动面位置和形状可以大大提高理论方法的分析精度。不同随机场模拟得到的边坡滑动面位置和形状及失稳风险可以帮助工程师预测和解释实际场地的边坡滑动面位置和形状,从而提高滑坡危险性评价的准确性。
