基于调制宽带转换器的特定辐射源识别算法

解建兰

（四川大学电子信息学院，成都 610065）

0 引言

特定辐射源识别（Specific Emitter Identification，SEI）通过比较射频指纹（Radio Frequency Fingerprints，RFF）特征[1]自动检测发射器。SEI 技术在认知无线电、军事通信和自组织联网中有许多应用。辐射源识别过程包括三个主要阶段：提取射频指纹、比较特征、匹配类别[2]。

我们从文献中了解到，可以对瞬态信号或稳态信号执行SEI 技术。基于瞬态的方法提供了良好的识别性能，并且从接收到的瞬态信号中提取了RFF 特征[3]。通过检测噪声的起点和终点来提取瞬态信号特征，但由于持续时间非常短，因此很难捕获瞬态信号。另外，非理想和复杂的信道条件很容易干扰瞬态特征，这可能会对识别结果产生负面影响。

稳态信号提供了统计上更稳定的RFF[4]。在高阶频谱和时频特性中已经研究出了许多特征提取方案，例如双谱、累积量和短时傅立叶变换。在文献[1]中，Zhang 等人提出了基于经验模式分解（Empirical Mode Decomposition，EMD）的熵、一阶和第二阶矩（EMDEM）识别算法。Udit Satija 等人发现EMD 的主要缺点是存在模式混合问题，为了解决该问题，他们使用变分模式分解（Variational Mode Decomposition，VMD）以及一组时间和光谱特征作为SEI 的指纹。他们提出了三种基于VMD 的SEI 算法，其中效果最好的是频谱平坦度（Spectral Flatness，VMD-SF）算法[2]。

在最近的几十年中，短触发低概率拦截信号经常出现在现代电子战环境中，并且这种信号寿命短且难以拦截。对于这种类型的信号，文献[2]中的三个主要缺点是：高采样率、大量采样数据以及需要载波频点先验知识、信号的RFF 特征不能被准确地提取。本文提出将调制宽带转换器（Modulated Wideband Converter，MWC）[5]应用于SEI 领域很好地解决了这些问题，并为之后SEI 的研究提供了新的思路。MWC 使用周期性伪随机序列（Pseudo Random Sequence，PRS）将接收到的信号频谱混合到基带中，混合信号通过低通滤波器（Low Pass Filter，LPF）和模数转换器（Analog to Digital Conversion，ADC），以获得包含接收信号所有信息的压缩采样数据（Compressed Sampled Data，CSD）。由于SEI 只关心信号中包含的原辐射源的射频指纹特征，并不关心接收信号的具体形态，故我们可以直接从获得的CSD 中提取识别特征，而无需重构原始信号。

1 系统模型和MWC

1.1 系统模型

SEI 的目的是通过提取传输信号所携带的特定信息、特征来区分发射器。功率放大器（Power Amplifier，PA）[2]是发射机的重要组成部分。PA 固有的非线性和记忆效应会导致发射信号发生严重的非线性失真，其非线性系统响应特性是导致发射器特定特征（也称为指纹）的主要原因。PA 的系统响应通常表示为泰勒多项式模型，令Ls为泰勒多项式的阶数，对于辐射源q的功率放大器的输出可表示为：

其中：

gt是PA 的输入信号，其中st为在时间t处的基带调制信号，f为载波频率，T为采样周期，是泰勒多项式的系数。可以看出，对于不同的辐射源q，具有相同的阶数Ls时，不同的泰勒多项式的系数表示辐射源指纹。Γ[q](gt)表示辐射源q功率放大器的输出信号，即辐射源q的发射信号，该信号携带了辐射源q的特定信息。

接收端不知道信号来自哪个辐射源，故不使用符号来表示接收信号x(t)对辐射源q的依赖性，接收信号可以表示为：

其中φ[q]是从辐射源q到接收机的信道衰落系数，这在接收端是未知的，ωt是加性噪声。在MWC 接收机处，接收信号x(t)被压缩采样获得CSD，直接从中提取特定于辐射源的特征来区分不同的辐射源，而无需重构信号。

把式（1）代入式（3）可以把接收信号x(t)表示为：

1.2 MWC模型

MWC 的总体结构如图1 所示，这个系统包含m个欠采样通道，本文中i=1,2,…,m，i表示第i个采样通道。接收信号x(t)同时进入每个采样通道与周期为Tp的PRS 相乘，pi(t)每个周期内有Np=Tp fNyquist个元素。混合信号ri(t)使用具有截止频率为fp2 的LPFh(f)进行滤波，以获取滤波后的信号wi(t)。最后信号wi(t)经过一个速率为fs=1Ts的低速ADC 得到压缩采样数据yi[n]。图1 中的LPF 和ADC 要满足严格的设计要求才能使每个子频带扩展至整个频域，才能使各个子频带相互混频搬移至目标基带内。伪随机信号pi(t)的周期频率为fp=1Tp，频谱切片和频谱搬移的带宽大小由fp决定。

在每个频带宽度为B的频段中都包含整个频带的所有信息，即MWC 能把载频未知的信号随机混频搬移到低频窄带中。MWC 先把混频信号ri(t)经过LPF 滤波，使得频谱只留下f∈[-fp2,fp2]内的信息而去除掉其他范围内的频谱，再进行ADC 低速采样，有效降低了后端的ADC 采样速率，减少了压缩采样数据，使得后续能够实时处理。

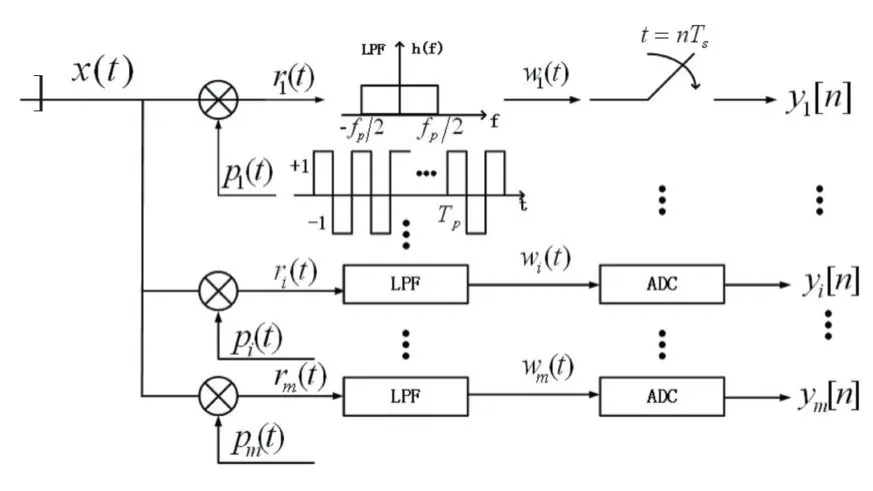
图1 MWC系统原理框图

2 基于CSD的辐射源个体识别算法

本文提出的基于MWC 的频谱偏度（Spectral Skew⁃ness，MWC-SSn）算法通过测量CSD 的傅里叶变换频谱的均匀性，提取出傅里叶变换谱中显示的特定于辐射源的特征。信号x(t)经过MWC 系统压缩采样之后变成了一个M×N维大小的矩阵V对其进行傅里叶变换可得变换之后的矩阵Bu,v

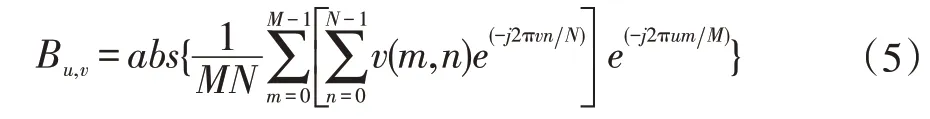
其中abs(∙)表示取绝对值操作。

提取Bu,v一阶矩测量CSD 频谱的平均强度，定义为：

其中u,v分别表示矩阵Bu,v的行数和列数，式矩阵的大小。

提取Bu,v二阶矩测量CSD 频谱的偏度，定义为：

MWC-SSn 算法流程

训练过程：设Vi,i=1,2,…,是训练序列i的矩阵，其中是所有Q类训练序列的总数。

1：根据式（5）算出每个序列的傅里叶变换绝对值矩阵Bi；

2：根据式（6）计算出每个序列一阶矩测量CSD 频谱的平均强度；

3：根据式（7）计算出每个序列二阶矩测量CSD 频谱的偏度；

4：构成训练序列i的训练特征向量集是每个类的标签，使用训练集去训练SVM 分类器；

识别过程：设Vl,l=1,2,…,N是未知类别的第l个测试序列矩阵，其中N是测试序列的数目。

5：根据式（5）-（7）计算出Vl的一阶矩测量 CSD 频谱的平均强度和二阶矩测量CSD 频谱的偏度

6：获得测试序列l的测试向量为

7：根据SVM 分类器给予特定类别的多数选票来确定辐射源类别。

3 数值仿真实验

在本节中，我们将所提出的算法性能与当前SEI领域最佳算法 EMD-EM[1]、VMD-SF[2]的性能进行比较。我们评估在AWGN 信道下不同数量的辐射源识别性能。在本文中，我们像文献[1-2]中分别研究了2个、3 个和4 个辐射源的情况。用正确识别的概率（pcc，Probability of correct classification）分析了所提出算法的性能。考虑到所有辐射源Q都是等概率的，可以将正确分类的总概率表示为：

实验参数设置见表1。

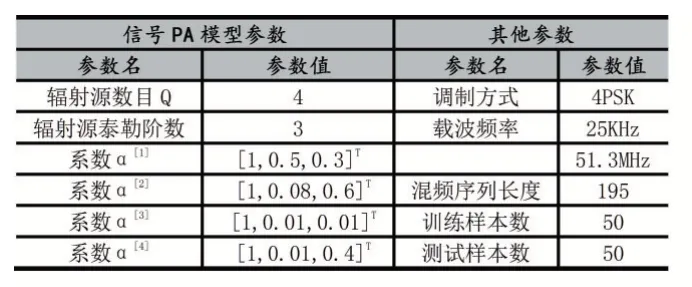
表1 参数设置

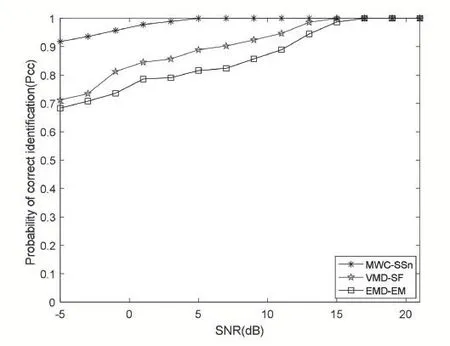
图2 Q=2时的辐射源识别性能

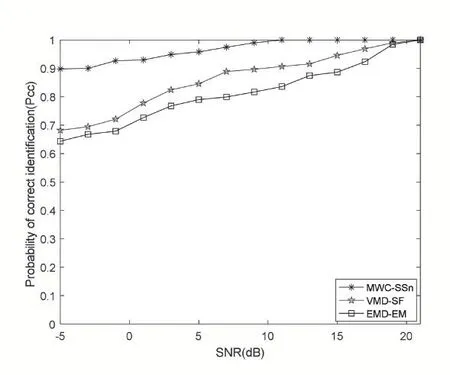
图3 Q=3的辐射源识别性能

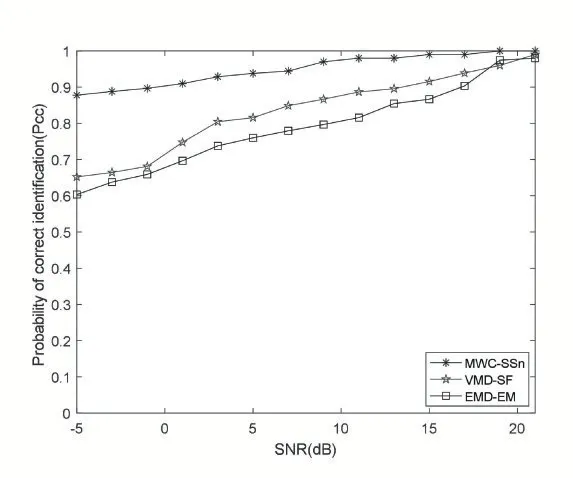
图4 Q=4辐射源识别性能

图2-图4 说明了2 个、3 个和4 个辐射源情况下SNR 和识别率的关系。与EMD-EM、VMD-SF 算法相比，所提出的MWC-SSn 算法在低SNR 和增加辐射源数量的情况下也具有出色的性能。从这三个图可以看出，辐射源识别性能随SNR 值的增加而提高，随辐射源数目增加而略微降低，这是由于辐射源数目越多区分难度越高。在图2 中，对于2 个辐射源的情况，MWC-SSn 算法在 SNR=5dB 时识别率达到 0.97，而EMD-EM 和VMD-SF 算法识别率均低于0.9。在3 个辐射源情况下，MWC-SSn 在SNR 为8dB 时识别率为0.96，同等条件下另外两种算法识别均低于0.91。同样的在4 个辐射源情况下，在每个SNR 下本文提出的算法的识别率均高于另外两种算法。因此在需要实时准确识别辐射源个体的场景中MWC-SSn 算法具有较大的优势。

4 结语

在本文中，我们使用MWC 亚奈奎斯特采样接收机来获取包含发射信号的所有信息的CSD。基于MWC接收机，我们可以实现亚Nyquist 率压缩采样，降低硬件实现的复杂性并减少后端处理数据量，解决了辐射源个体识别中处理数据量大、不能实时处理的问题。我们通过直接处理CSD 提出了基于MWC 的频谱偏度特征辐射源个体识别算法。通过与EMD-EM、VMDSF 进行比较，证明了MWC-SSn 算法的优越性。与现有的基于模式分解的方法相比，本文提出的算法在低信噪比、多目标下提供了出色的辐射源个体识别性能。