基于PSO-HJ算法的多无人机协同航迹规划方法

单文昭，崔乃刚，黄 蓓，王小刚，白瑜亮

（1.中国运载火箭技术研究院，北京 100076；2.哈尔滨工业大学 航天学院，哈尔滨 150001）

多无人机协同航迹规划是任务规划系统中的关键部分[1]。多无人机协同任务包括目标协同定位、目标协同攻击和目标效能协同评估等。其中，多个无人机同时到达目标区域是目前协同攻击问题的主要研究方向[2]。

航迹规划是一类复杂优化问题，国内外学者提出很多算法。常用算法可大致分为两类，一类基于图的算法包括Voronoi图、A*搜索算法、D*搜索算法等[3]。另一类基于群体智能优化算法包括遗传算法、粒子群算法、差分进化算法等[4]。这类智能算法简单且计算效率高。其中，粒子群算法（Particle Swarm Optimization，PSO）不需要变异操作，比其他进化算法更易实现，但PSO存在局部搜索能力差的缺陷[5]。文献[6]通过引入收缩因子和学习因子到PSO中，改善二维航迹规划算法收敛速度。文献[7]通过将种群的繁殖机制引入PSO，提升算法全局搜索能力。文献[8]设计了异步变化的学习因子，提高了算法全局搜索能力。本文引入Hooke-Jeeves（HJ）搜索算法到PSO中，提出一种粒子群优化和HJ搜索算法相组合的PSO-HJ算法，丰富粒子搜索行为并改善粒子局部搜索能力。同时，对评价粒子优劣的方法做出改进，充分考虑不满足约束的粒子，避免由于过度舍弃而远离可行解。

多无人机协同航迹规划问题需要考虑的约束增多且模型更加复杂，对求解效率和速度要求更高[10]。目前，文献常用集中式求解框架解决多机协同问题，集中式求解框架相对简单且获得解的精度高。文献中这类方法考虑无人机数量较少或环境过于简单，如果无人机数量增加，计算维数将扩大，求解速度变慢，算法不适用于动态变化的场景。而且，真实场景中无人机可能存在通信受限情况，集中求解方法需要掌握信息过多，难以实际应用。针对这些问题，本文提出一种多无人机协同航迹规划方法的框架，先分别求解单机航迹规划问题再求解多机协同问题，将求解总体代价最小的问题转化为求取最小的协同时间。一个复杂的高维优化问题分解成一个计算量小的低维问题，提高计算效率。另外，传递协同变量编队预计到达时间ETA（estimate time arrival，ETA），节省传输时间和空间，更具有可实现性[11]。

1 无人机航迹规划问题建模

1.1 环境建模

无人机任务环境中威胁包括雷达、防空火炮、防空导弹等。一旦无人机穿越威胁区，无人机存在被击落的可能。本文将威胁区定义为圆柱体，威胁区为T=（xT,yT,hT,rT）。威胁中心坐标为（xT,yT），威胁区水平投影半径为rT，威胁区高度为hT。地形包括山丘和平原，因此设计地形函数为z=fT（x,y）。地形示意图如图1。

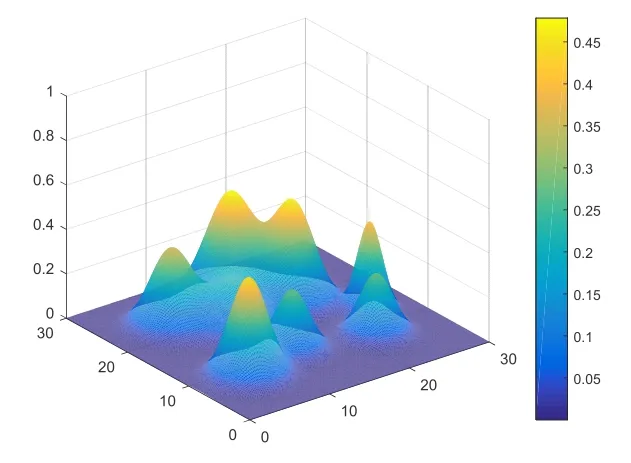
图1 地形示意图 Fig.1 Topographic map

1.2 航迹代价函数

本文航迹代价函数包括威胁代价、航程代价、高度代价、撞地概率代价函数。

1.2.1 威胁代价函数

威胁代价是无人机全程飞行中穿越威胁区的可能性。按图2所示，在第i个航迹段wiwi+1取k个点，记Pi=（pi,1,pi,2,pi,3…pi,k）。威胁代价按照式(1)计算。

其中，n为航迹段个数，m为威胁源个数。lTi是第i段航迹被威胁区覆盖的长度。fTAj（pi,q）是pi,q点受到第j个威胁的影响程度，按照公式(2)计算。

其中dj是航迹段上当前节点到第j个威胁源中心的距离。

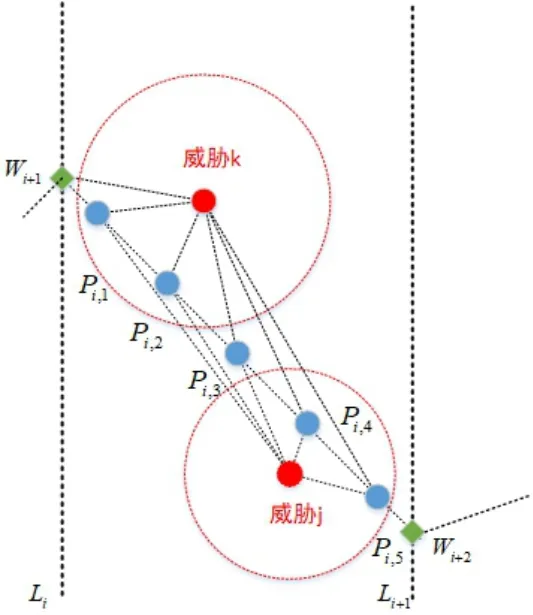
图2 威胁代价计算示意图Fig.2 Schematic of threat cost calculation

1.2.2 航程代价函数

航程是无人机从起始点到指定目标点需要飞过的空间距离。通过缩短航程，既能降低无人机危险系数，也能节省燃油。航程代价函数为：

其中li是第i个航迹段长度。

1.2.3 高度代价函数

低空飞行能降低无人机被敌方雷达发现的概率。所以，要求无人机在满足地形最小离地高度条件下，以尽可能低的高度飞行，利用地形实现隐蔽。为表达简洁，用fT表示fT（xi,yi），高度代价函数为：

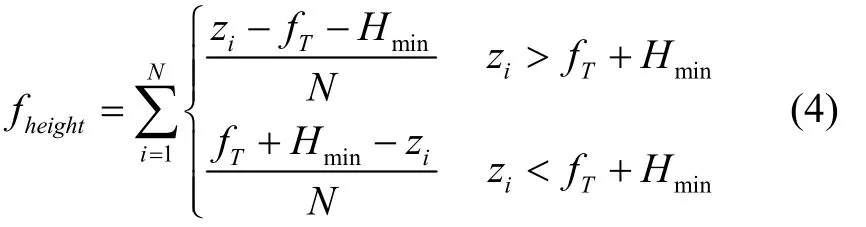
其中，N是无人机航迹上取点的个数，（xi,yi,zi）是无人机当前位置坐标，fT(xi,yi)是航迹曲线上任意一个航迹点（xi,yi）对应的地形高度，Hmin是无人机允许最低飞行高度。

1.2.4 撞地概率代价函数

撞地代价函数是航迹曲线穿过地形的航迹点总数。

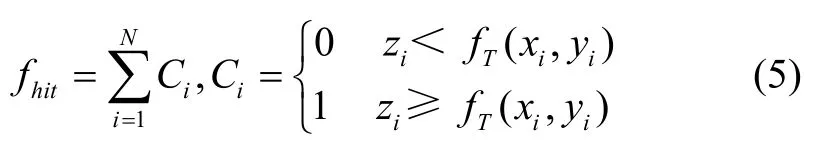
综上所述，无人机航迹代价函数如式(1)

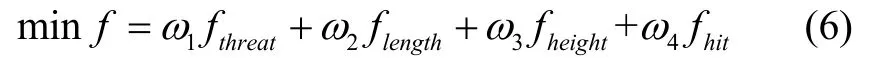
其中，ω1～ω4是评价指标的权重系数，且满足。根据不同的无人机任务，权重系数不同。评价指标越重要，对应的权重系数越大。

1.3 约束条件

1.3.1 最短航程约束

无人机调整飞行姿态前，第i个航迹段li需满足大于最短直飞距离lmin。该约束表示为：

1.3.2 最长航程约束

无人机携带燃料有限，存在最长航程限制。设lmax是允许的最长航程。该约束表示为：

1.3.3 最大水平拐弯角约束

无人机性能限制其只能在有限的拐弯角内转弯。设φmax为最大允许拐弯角，记ai=（xi-xi-1,yi-yi-1）T是第i段航迹水平投影。该约束表示为：

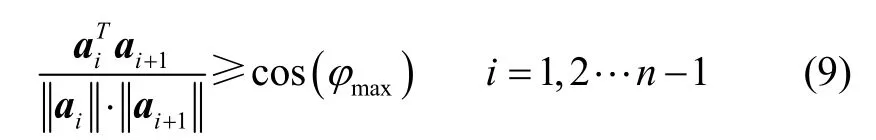
1.3.4 最大爬升角或俯冲角约束

无人机爬升或俯冲最大高度受到自身机动性能的影响。设θmax是允许最大爬升角或俯冲角，该约束表示为：

1.3.5 最低飞行高度约束

无人机飞行过低会增加地面碰撞概率，该约束为：

2 单无人机航迹规划的PSO-HJ算法

2.1 基本粒子群算法

粒子群算法（Particle Swarm Optimization，PSO）由Eberhart和Kennedy于1995年提出，PSO算法是采用群体智能思想的全局优化算法，借鉴模仿鱼群和鸟群的集体行为，利用粒子间之间合作和竞争达到计算最优解的目的[12]。每个粒子都代表一个解，在D维搜索空间中，第i个粒子位置向量为xi=（xi1,xi2…xiD），第i个粒子速度向量为vi=（vi1,vi2…viD），经过t+1次迭代后，粒子xi历史最佳位置为，种群全局最佳位置。粒子速度和位置更新公式为：

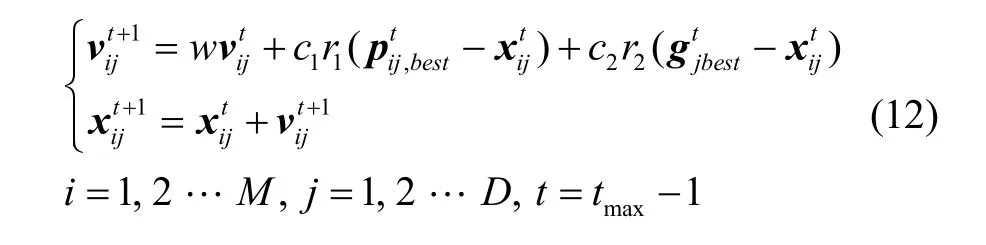
其中，w是惯性权重系数，c1和c2分别是粒子的学习因子和加速因子，r1和r2是（0,1）之间的随机数且服从均匀分布，M是种群规模，D是粒子的维数，tmax是粒子的最大迭代次数。速度和位置有最大速度和最大位置限制。

图3 粒子群算法原理图Fig.3 Schematic of particle swarm optimization

2.2 约束处理机制

无人机航迹规划问题可转化为如下非线性规划问题。

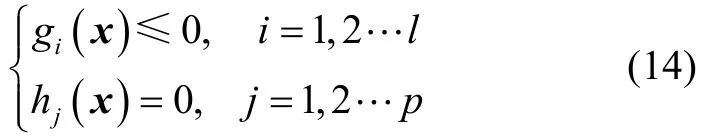
其中，J是适应度值。f（x）是适应度评价函数，具体参考式(6)，g（x）是不等式约束，l是不等式约束的个数，h（x）是等式约束，p是等式约束的个数。这里只考虑不等式约束。为处理约束，引入约束违反度函数fv（x）：

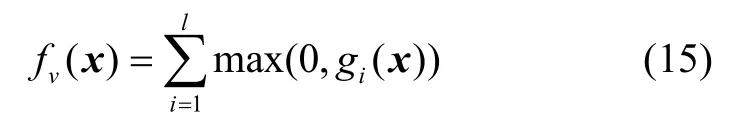
传统评价粒子的方法不考虑违背约束的粒子。本文对评价粒子优劣的方法做出改进，避免由于过度舍弃而远离可行解。基于比较准则提出新的粒子评价机制为：

（1）当粒子xi和粒子xj都满足约束时，如果f（xi）＜f（xj），则xi个体为优，否则xj个体为优。

（2）当粒子xi和粒子xj都不满足约束时，如果fv(xi)＜fv（xj），则xi个体为优，否则xj个体为优。

（3）当粒子xi满足约束，粒子xj不满足约束时，如果fv（xj）＜εv且f（xj）＜f(xi)，则xj个体为优，否则xi个体为优。εv是要求的精度指标。

2.3 单无人机航迹规划的PSO-HJ算法

粒子群算法的惯性权重越大全局搜索能力越强，反之，惯性权重越小，局部搜索能力越强。与传统PSO算法不同，本文惯性权重不是固定值，惯性权重线性下降公式为：

其中，根据经验wmax= 0.95，wmin= 0.4，ω是惯性权重，ωmax是最大权重，ωmin是最小权重 ，t是粒子的当前迭代次数[13]。

在PSO算法搜索过程中，粒子速度可能会超出最大速度限制，此时速度更新公式为：

粒子位置可能会超出解空间的边界，此时位置更新公式为：

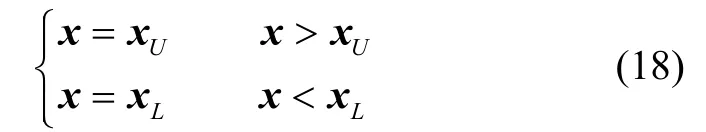
其中，v是粒子当前速度，xU是粒子位置的边界值上限，xL是粒子位置的边界值下限。

HJ算法是一种无需梯度计算的直接搜索算法。HJ算法先探索下降的最有利的方向，然后沿着这个方向加快搜索速度，可以迅速获得局部最优解。粒子群算法是随机搜索算法，所以局部搜索能力较差，PSO和HJ混合能丰富优化过程的搜索行为，有利于收敛到最优解。改进的混合算法称为PSO-HJ算法。PSO-HJ算法步骤可以描述为：

（1）初始化：确定种群规模M、粒子维数D、最大迭代次数tmax。初始化粒子速度、位置和PSO参数。

（2）根据式（14）计算粒子的适应度值，根据新的粒子评价机制，得到粒子历史最佳位置pbest和粒子全局最佳位置gbest。

（3）更新粒子速度和位置，并更新粒子历史最佳位置pbest和粒子全局最佳位置gbest。

（4）如果粒子下一代适应度值大于粒子当代适应度值，进入到第（6），否则进入第（5）。

（5）选择前百分之二十的粒子引入HJ算法 ：将PSO算法的解赋予HJ算法作为初始值，利用HJ算法更新PSO的解。然后进入到第（6）。

（6）对于超出边界的粒子按照公式更新其速度和位置，保证速度和位置满足要求。

（7）判断是否满足结束条件：达到设定的最大迭代次数或达到精度要求。如果满足，停止迭代，输出最优解。否则，回到第（2）。算法流程图如图4所示。

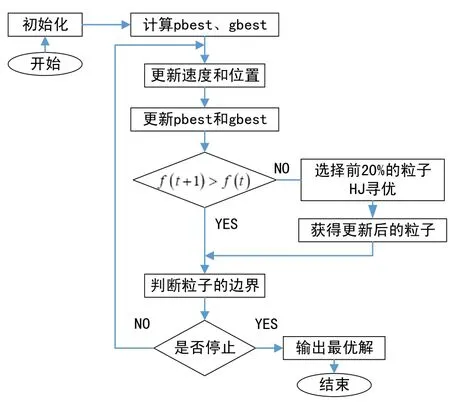
图4 PSO-HJ算法流程图Fig.4 Flow chart of PSO-HJ algorithm

3 多无人机协同航迹规划方法

3.1 多无人机协同航迹规划方法框架

本文协同航迹规划的任务是多无人机协同攻击目标，要求编队同时到达时间最短。定义协同变量为编队预计到达时间（estimate time arrival，ETA）。多无人机协同航迹规划问题可以通过层次分解法，转化为先求解单机航迹规划问题再求解多机协同问题。多机协同规划算法的框架包括三个层次，每个层次之间互相传递信息，框架如图5所示。

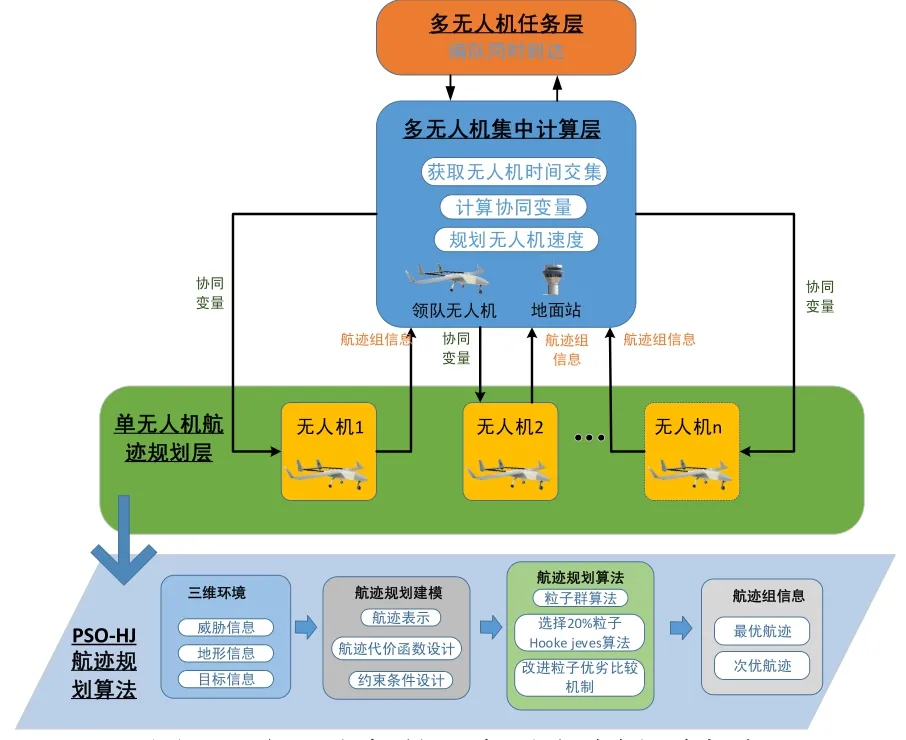
图5 多无人机协同航迹规划方法框架Fig.5 Framework of multi-UAV cooperative track planning method

（1）第一层是多无人机任务要求层。任务为多无人机协同攻击目标，要求多无人机同时到达目标。

（2）第二层是多无人机集中计算层。集中计算层为中央单元，包括领机或者地面指挥站等，利用时间协同航迹规划算法计算编队到达时间和无人机速度。

（3）第三层是单无人机航迹规划层。利用PSO-HJ算法求解最优航迹和备选航迹信息，作为多无人机集中计算层的输入信息。

3.2 多无人机时间协同航迹规划算法描述

假设第i架无人机速度变化范围为。其中，是第i架无人机的最小飞行速度，是第i架无人的最大飞行速度。因为航迹规划空域里无人机速度变化较小，理想假设无人机匀速飞行。根据前文航迹规划方法获取无人机航迹组信息，包括最优航迹和多条备选的次优航迹。那么可知第i架无人机如果按照最优航迹飞行，该无人机预计到达时间范围Stime,i为：

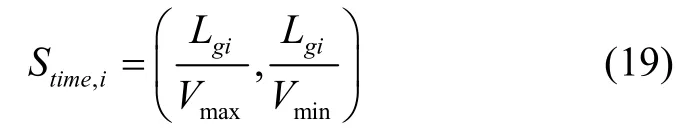
其中，i= 1,2…s，s是无人机的数量。Lgi是第i架无人机最优航迹长度。同理可计算无人机选择其他备选航迹的预计到达时间范围。

无人机编队需要实现最短时间同时到达，协同变量ETA的计算公式为

协同变量ETA是所有无人机预计到达时间集合交集的最小值。若编队预计到达时间ETA无解，则取预计到达时间Stime,i最短的无人机的次优航迹Lci替换其当前航迹Li，重新计算该无人机预计到达时间Stime,i。如果仍无解，重复以上步骤直至协同变量ETA有解。求解得到编队到达时间Tf后，可分配第i架无人机速度为Vi=LfiTf，Lfi是满足时间协同的无人机航迹。具体无人机协同航迹规划算法流程如图6所示。

图6 多无人机时间协同航迹规划算法流程Fig.6 Flow chart of multi-UAV time cooperative flight path planning algorithm

多无人机时间协同航迹规划算法可以描述为：

（1）根据式（1）到式（18）同时计算每架无人机的最优航迹和备选的次优航迹组。

（2）将（1）计算得到的结果作为协同规划层的输入，根据式（19）计算每架无人机到达时间范围Stime,i。如果ETA无解，进入（3）。否则，进入到（4）。

（3）选择预计到达时间最短的无人机次优航迹Lci替换该无人机当前航迹Li，进入到（2）。

（4）根据式（20）计算协同变量ETA。

（5）由Vi=LfiTf计算每架无人机飞行速度Vi。

（6）分配速度Vi和协同航迹Lfi至第i架无人机。

4 仿真分析

4.1 仿真初始条件

仿真实验环境为 Dell PC，Core E5800 CPU(3.2GHz)，4G内存。无人机的任务区域是30km×30 km×30 km的立方体。3D地形内有很多山和平原，威胁的覆盖以圆柱体表示。本文设计仿真场景包括5个威胁。设定初始种群规模M= 100，粒子维数D= 21，最大迭代次数tmax=200，最大权重ωmax= 0.95，最小权重ωmin= 0.4。最大拐弯角φmax= 60°，最大爬升角θmax= 60°，最低飞行高度Hmin= 20m 。

4.2 仿真结果

仿真算例1：

为验证PSO-HJ算法的多无人机时间协同三维航迹规划方法的可行性，仿真结果如图7-8所示。

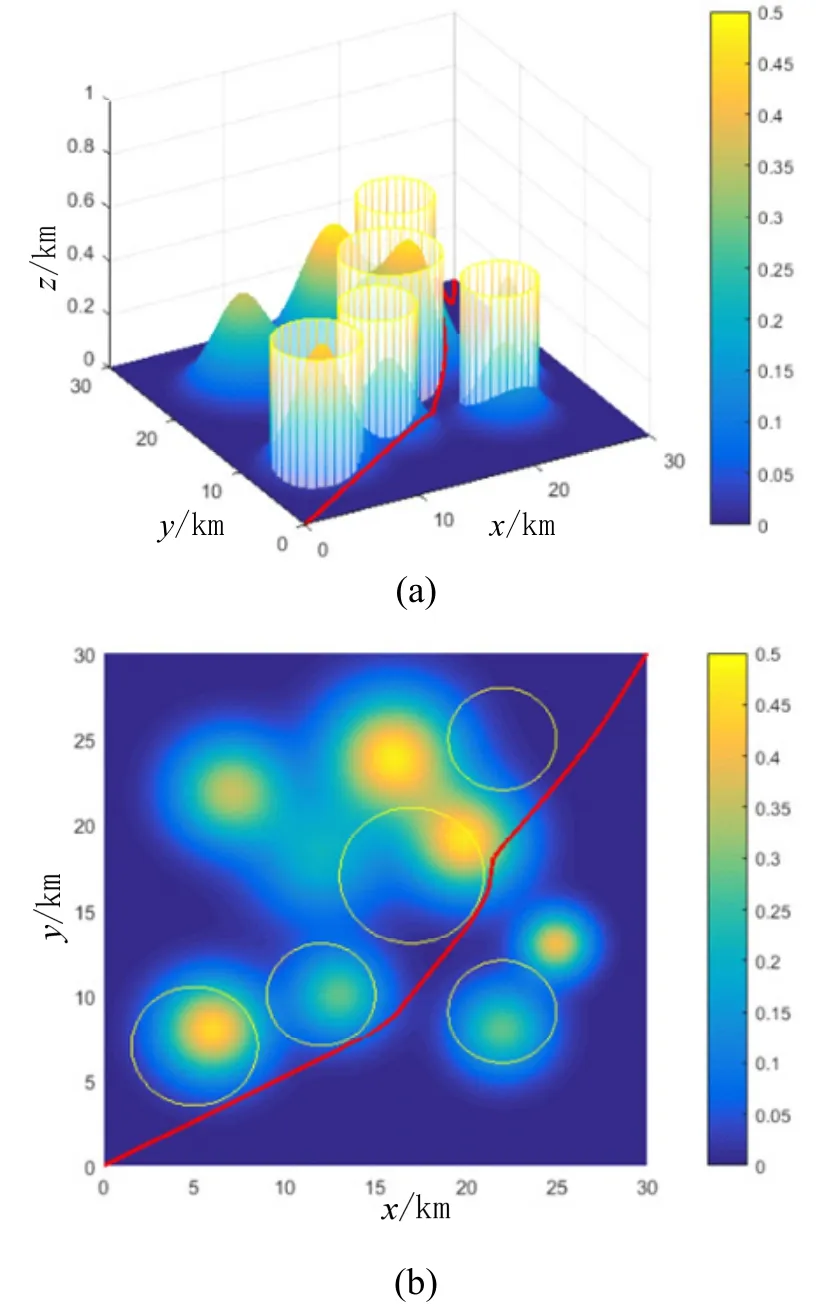
图7 基于PSO-HJ算法的单无人机航迹结果Fig.7 Single UAV path planning results based on PSO-HJ algorithm

图8 多无人机时间协同航迹结果Fig.8 Multiple UAV time cooperative path planning results

仿真结果表明，算法可行性得到验证。从图7看出，无人机规划航迹避开威胁区，以尽量低高度飞行并较好的跟随地形。从图8可以看出，本文提出的方法实现多架无人机同时到达目标。

仿真算例2：

为验证PSO-HJ航迹规划算法的效率，与传统PSO和量子粒子群（QPSO）航迹规划算法比较。算法效率的评价指标包括直线率系数和最优适应度值。本文定义了航迹规划算法的评价指标直线率系数SLR，直线率系数决定了航迹整体长度与最短直线距离接近的程度。直线率系数越高代表航迹规划算法性能越好。直线率系数，SG代表从无人机出发点到目标点的直线距离，luav是无人机规划后的航迹长度。仿真结果如图9- 10所示。PSO、QPSO和PSO-HJ算法计算20次后算法评价指标结果如表1所示。

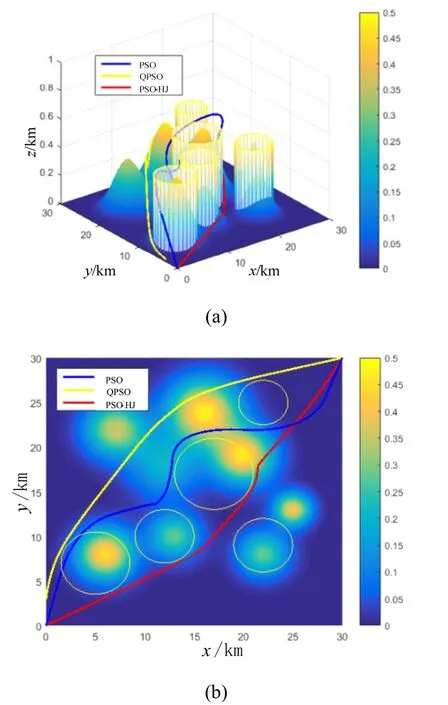
图9 PSO、QPSO和PSO-HJ算法的航迹比较结果Fig.9 Path planning results comparison of PSO,QPSO and PSO-HJ algorithms

仿真结果表明，PSO-HJ算法比PSO算法和QPSO算法收敛速度更快。图9可以看出，PSO-HJ算法生成的航迹更短，而且地形跟随效果更好，PSO生成的航迹选择爬过高山，而PSO-HJ算法选择较低的高度飞行。从图10可以看出，PSO-HJ算法最优适应值更低。从表1可以看出，PSO-HJ算法的航迹代价和航迹长度都低于PSO和QPSO算法。PSO-HJ算法的精度比QPSO算法精度提高了20.85%，比PSO算法精度提高了58.14%，说明PSO-HJ算法得到的解的质量更高，PSO-HJ算法的局部搜索能力更好。

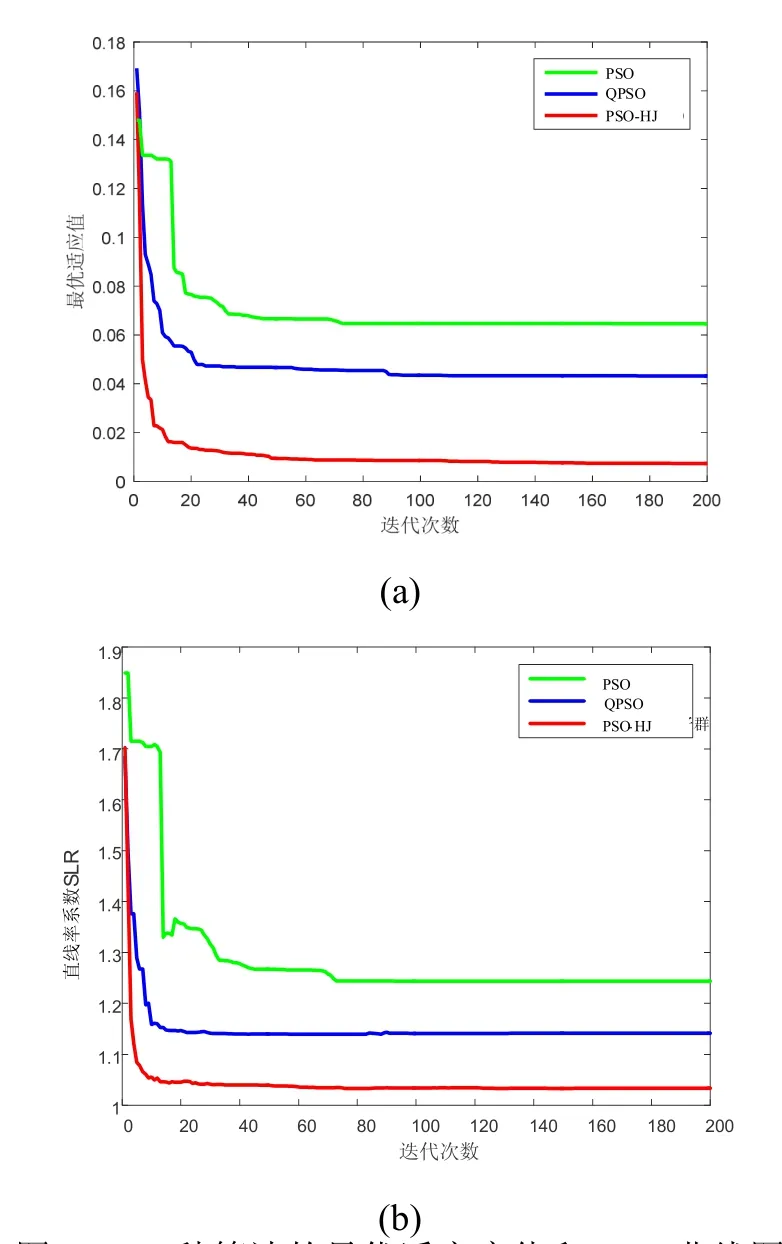
图10 三种算法的最优适应度值和SLR曲线图Fig.10 The optimal fitness value and SLR curve of the three algorithms

表1 航迹规划效果的算法比较Tab.1 Algorithm comparison of flight path planning effect

5 结 论

本文分析和设计了无人机航迹代价函数，结合无人机动力学特性设计了约束条件，建立了单无人机三维航迹规划数学模型。

为处理复杂优化问题，设计了基于PSO-HJ算法的无人机的三维航迹规划方法。提出了新的粒子评价机制，并对表现差的粒子引入HJ算法，来改善化算法的效率。

设计多无人机协同航迹规划方法框架，基于PSO-HJ算法求解备选航迹，通过多无人机集中航迹规划层协调编队到达时间实现协同航迹规划。

仿真结果表明，本文提出的算法实现了多架无人机同时到达目标区域，证明了算法可行性；与PSO算法和QPSO算法相比，具有更快的计算速度和收敛精度。