基于交叉验证支持向量机储层预测方法及应用

张军华, 任雄风, 赵 杰, 谭明友, 于正军

(1.中国石油大学(华东)地球科学与技术学院，青岛 266580；2.胜利油田物探研究院，东营 257022)

东营凹陷中浅部储层油气勘探，大多都形成了技术系列与规范。而深部储层其成因及成藏机制的研究还不够深入，地震资料品质相对较差，钻遇井又比较少，储层厚度预测有较大的困难。

储层预测有很多方法，支持向量机方法(SVM)由于能很好地解决样本少、非线性、高维数和局部极小点问题[1]，对于少井区的储层预测，是值得优先使用的方法[2-3]。SVM最早由Vapnik根据模式识别中广义肖像算法发展而来[4-5]，随着对ε不敏感损失函数的引入[6]，学习性能得到提高，在建模、预测等方面取得了很好的应用效果[7-9]。邹华胜等将SVM引入少训练样本的储层厚度预测中，预测相对误差较BP人工神经更小[10]。张长开等通过SVM的属性优选方法选出有效属性，基于SVM对储层进行了有效预测[11]。林年添等利用聚类分析法对用卷积升维形成的各类纵、横波地震属性进行降维，将用聚合法得到的多波地震聚合属性作为SVM的学习集进行含油气储层预测，预测储层边界更加清晰与实际情况较吻合[12]。SVM储层预测，关键因素有两个：一是选好核函数，本文采用的是适用于高维、小样本的高斯径向基函数；二是调好核函数参数g和惩罚因子C，它们会直接影响SVM泛化能力和预测精度[13-14]。为了使每口井都能参加训练并且得到验证，在选取惩罚因子和核函数参数的训练过程中应用了交叉验证方法[15]，进一步提高了储层厚度的预测精度。

1 东营深部储层井震关系分析及属性优选

1.1 东营深部储层特征及机理分析

东营凹陷深层发育紫红色泥岩或棕红色砂岩，地质界称其为“红层”。由于年代老、埋深大，砂、泥岩波阻抗差异较小，地震反射相对较弱，砂体叠置，致使其研究具有很强的挑战性，研究成果对拓展油气勘探领域有重要科研及生产价值。

如图1所示为研究区王古9井(钻遇红层)的过井剖面，可以大致将地层范围分为红层上覆地层、红层和红层下伏地层，可以看到，红层以上地层和红层以下中生界地层成层性都很好，但是中部红层成层性反而低。结合该井目标层段——孔一段录井资料(图2)，可见其速度结构复杂，测井曲线抖动非常多，综合地震相特征分析，说明红层是以速度变化很大的薄互层为典型特征。

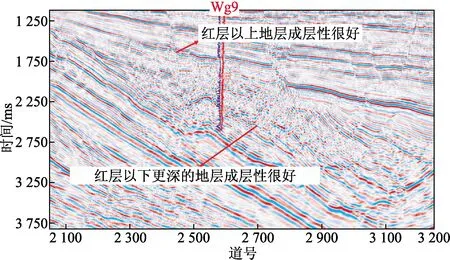
图1 研究区王古9井过井剖面

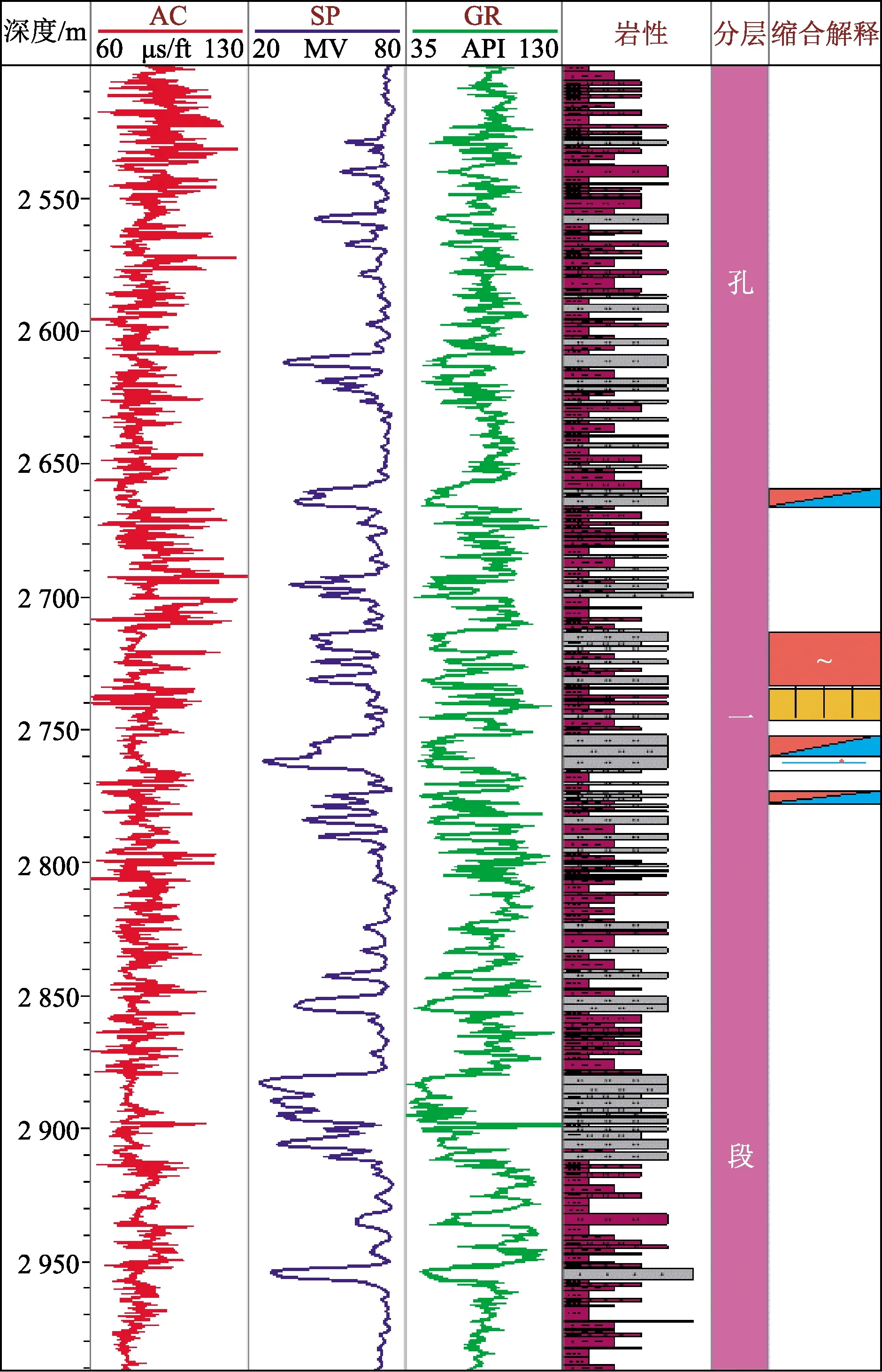
图2 王古9井孔一段录井图

研究区埋深较大，多在3 000 m以上；而面积较大(586 km2)，钻遇目标层的井却很少，有可靠测井数据的只有三十几口。储层埋深大、层薄、成层性差，地震资料分辨率不够高，加上钻遇井少等多种因素，决定着储层预测有很大的难度。

1.2 地震属性的提取及优选

地震属性是地震数据经过数学变换而得来的有关地震波几何学、运动学、动力学或统计特征，地质含义明确的地震属性常与储层有一定的对应关系。对于孔一中储层，提取振幅、频率、相位等12种沿层属性，利用基于核相似性度量的特征选择方法，优选出带宽、能量半时、最大振幅、均方根振幅、过零点个数和弧长等6种地震属性，用于样本训练。它们的物理意义和地质含义是明确的：带宽是指优势频带的宽度，与地震资料的品质相关性较大；能量半时属性反映了分析时窗内能量相对变化关系，能够指示沉积环境与岩性岩相变化；最大振幅适合于岩性分析及砂岩百分比研究，储层含油气后一般振幅会增强；均方根振幅间接地反映了地震反射系数的大小，可以用来指示地下岩性的变化；过零点个数属性能够较好地描述地震波振幅过零点的个数，包含了岩性、流体等信息；弧长属性是指时窗内地震道波形的长度，对于阻抗差较大的储层反映效果不错。

如图3所示为6种地震属性和孔一中井点厚度图。笼统地看，带宽、能量半时、最大振幅、均方根振幅、过零点个数和弧长6种地震属性，对孔一中的储层局部均有较好的相关度，但单个属性还不能全面描述整个工区储层变化。为此，要建立井点厚度与属性的定量关系，用SVM来进行训练和预测。

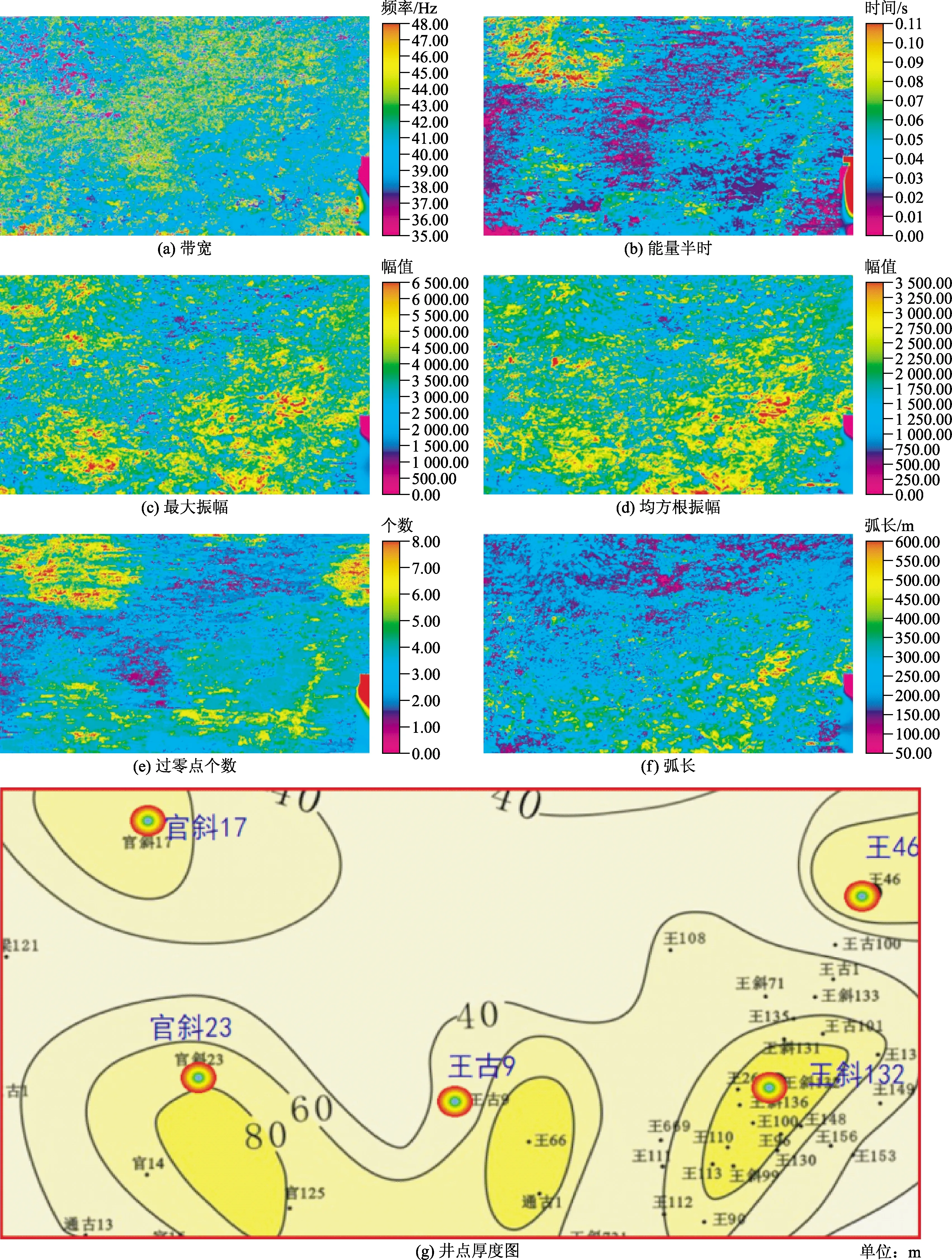
图3 孔一中地震属性及井点厚度

2 基于交叉验证的SVM储层预测方法

2.1 方法原理

给定样本集{(xi,yi),i=1,2,…,m},其中xi是输入数据，yi是与之对应的标签值，m为样本个数。SVM回归具有稀疏性，若样本点与回归模型足够接近，即落入回归模型的间隔边界内，则不计算损失，对应的损失函数被称为ε-不敏感损失函数：

error[y,f(x)]=max[0,|f(x)-y|-ε]

(1)

式(1)中:ε是决定边界宽度的超参数，训练学习就是为了使构造的函数f(x)与输入数据对应目标值y的距离小于ε。当样本集为非线性时，SVM首先在低维空间中完成计算，而后经过核函数φ(x)将输入数据x映射到一个高维线性空间，在高维线性空间中完成回归模型的构建，即：

f(x)=ω·φ(x)+b

(2)

式(2)中：ω是权重向量；b是偏置项。

SVM回归为式(3)所示的二次凸优化问题：

(3)

由于ε-不敏感损失函数采用max并非处处可导,微分时会有问题,因此使用松弛变量ξ、ξ*进行表示，可得:

(4)

式(4)中：C为惩罚因子；ε为误差上限。通过引入拉格朗日因子α、α*、μ、μ*，可得式(4)的拉格朗日函数[式(5)]和式(6)所示的对偶优化模型：

L(ω,b,ξ,ξ*,α,α*,μ,μ*)=

(5)

(6)

式中：φ(xi)φ(xj)为核函数，可记为k(xi,xj)。上述对偶问题有如式(7)的KKT条件(一组解是最优解的必要条件)：

(7)

对该对偶问题进行求解，可以得到如式(8)所示的SVM回归函数形式：

(8)

由式(8)可知，将非线性样本从低维映射到高维空间只需要计算核函数k(xi,xj)，核函数有多种，选择高斯径向基函数，如式(9)：

g>0

(9)

由上述可知，SVM的训练过程中有两个重要参数：惩罚因子C和核函数参数g。惩罚因子C用来控制目标函数两项间的权重，其值大小将影响回归模型的泛化能力。核函数参数g取值偏小，高次特征衰减速度会很快，可降低空间维数；若取值偏大，则会出现过拟合。在对储层厚度进行预测时，C和g这两个参数的取值大小对预测精度至关重要，因此采用了交叉验证方法对二者进行选取，优选出最优参数。交叉验证用于评估模型的预测性能，尤其是训练好的模型在新数据上的表现，可以在一定程度上减小过拟合，还可以从有限的数据中获取尽可能多的信息。采用k折交叉验证法，通过对k个不同子集的训练结果进行平均来减少方差，使模型的性能对数据的划分不那么敏感。首先将训练集随机等分为k份，每次选取一份作为测试集，其他k-1份作为训练集进行模型训练，每次训练得到一个模型，在相应的测试集上测试，k组测试结果的平均值作为当前超参数(惩罚因子C和核函数参数g)下模型精度的估计。在超参数优选范围内进行训练，优选出精度最高的预测模型对应的超参数，再对全部训练集重新训练得到最优模型。基于交叉验证SVM储层预测具体步骤如下。

(1)设置惩罚因子C和核函数参数g的优选范围Cmin、Cmax、gmin、gmax，以及二者的优选步长ΔC、Δg。

(2)将训练集随机等分为n份，令C=Cmin,g=gmin,k=1,i=1。

(3)取第i组作为验证集，其他组作为训练数据。

(4)计算训练后在验证集上损失函数的大小εi。

(5)令i=i+1,若i≤n，转到(3)，否则转到(6)。

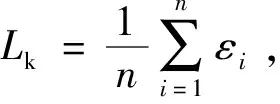
(7)令C=C+ΔC,k=k+1，若C≤Cmax，转到(2)，否则转向(8)。

(8)在计算出的损失误差Lk中选取最小值，其对应的超参数作为最优参数在整个训练集上重新进行训练。

2.2 实际资料应用

利用钻遇孔一中目标层的33口井，从中选取3口井验证储层预测效果。将优选出来的带宽、能量半时、最大振幅、均方根振幅、过零点个数和弧长等6种地震属性作为输入数据，以其他30口井点处的属性值及对应的储层厚度作为训练样本进行训练。惩罚因子C和核函数参数g的取值按照上述的交叉验证步骤在一定范围来优选，令n=6，经训练得到最优参数C=14、g=3。图4(a)为用C=14、g=3预测出来的应用工区的储层厚度，在表1中给出了预留下3口井的预测值以及与实际值的相对误差，误差都在10%以下。

如果不采用交叉验证优选出的参数C和g，预测精度会受到较大影响，图4(b)是使用非优选出来的参数C=14、g=1预测得到实际工区的储层厚度图，在表1中也给出了3口验证井出的预测值及其与实际值的相对误差大小，可以看到每口井的预测误差都有较大增幅，其中W113和Tg1井的误差都大于14%。结果表明，用交叉验证优选出的惩罚因子C和核函数g进行储层预测，可以有效提高预测精度。

表1 验证井储层预测厚度及误差统计

注：( )中为相对误差。

用线性拟合方法计算储层厚度，结果如图4(c)所示。从验证井的误差分析来看，交叉验证SVM方法要好于不采用交叉验证的SVM方法，但综合来看两种方法都要好于直接拟合的线性回归方法。

3 结论

东营凹陷孔一段储层埋深大、层薄、成层性差，地震资料分辨率不够高，加上钻遇井少，单一地震属性仅对储层局部有较好的相关度，不能全面描述整个工区储层变化。而SVM算法作为一种基于统计学理论的机器学习算法，在样本数少的情况下也拥有良好的学习能力和预测精度，要好于直接拟合的线性回归方法。但要充分发挥SVM的学习和预测性能，惩罚因子C和核函数参数g的选取至关重要，它们对预测精度影响较大。实际资料应用误差分析表明，交叉验证SVM方法有较好的预测精度，对中外深部储层预测有借鉴作用。