流体微团作用与流动结构变化试验分析

2020-06-13徐凯池张佳琪

航空发动机 2020年2期

徐凯池，张佳琪

（1.中国航发沈阳发动机研究所，沈阳110015；2.大连理工大学机械工程学院，辽宁大连116024）

0 引言

湍流流动广泛存在于航空航天、船舶、能源、动力、化工等领域[1-3]。在航空发动机的燃烧室中通常为湍流流动，其中已燃气体与未燃气体的掺混、燃烧与激波之间的相互作用以及湍流流动对化学反应的作用等对航空发动机性能有重要影响。拟序结构是湍流流动中最重要的结构，对湍流流动的维持、演化和发展起着重要作用。研究湍流流动可以为发动机结构设计提供理论基础，并为提高发动机性能提供有益参考。由于湍流中拟序结构在时间和空间尺度上的跨度以及运动特性十分复杂，一直是领域内的研究难点和热点。拟序结构主要包括条带结构和准流向涡、发卡涡/发卡涡包和超大尺度运动3大类[4-5]。其中高、低速条带结构的演化对湍流边界层摩阻和传热率等物理性质有重要影响，开展相关研究可以对湍流进行有效控制。

近年来，随着粒子图像测速（Particle Image Velocimetry，PIV）技术的迅猛发展，丰富的流场信息使研究者对湍流拟序结构的运动学特征和动力学过程有了更深刻的认识。顾大鹏等[6]通过PIV技术对双旋流燃烧室冷态流场进行测量，为进一步利用多级旋流器实现燃烧室内稳定燃烧、降低排放提供了依据；张欣等[7]利用PIV对双级旋流器燃烧室湍流流场进行测量，并得到旋流器几何参数对流场速度分布的影响；赵鹏等[8]利用PIV获得新型扩压器的内流场特征，为先进扩压器的结构优化提供了试验依据。进一步对湍流中拟序结构进行研究可以为湍流流场控制提供理论依据。Kline等[9]采用氢气泡流动显示技术观察到湍流边界层近壁区存在拟序运动，发现高、低速条带结构和湍流猝发现象，在试验中，近壁区高、低速条带结构沿流向移动并被拉长，在展向上交替排列呈现周期性变化；Asai等[10]通过平板试验人工构造了弯曲模式条带和肿胀模式条带，对条带失稳过程进行研究；Bai等[11]研究了条带结构变化与湍流减阻之间的关系；Skote等[12]基于条带不稳定性构建模型，通过数值模拟方法研究了湍流边界层中马蹄涡的产生机理；王双峰等[13]对圆柱尾迹影响下的湍流低速条带进行了试验研究；Smith[14]得到在湍流中条带结构展向平均间距约为100壁面单位。研究条带结构的变形有助于理解其失稳机理以及对壁面摩擦阻力的影响。通过数值方法构建条带或通过特定试验装置人工构造弯曲条带和肿胀条带，与工业工程实际流场中的条带结构有一定区别，同时，条带结构变化机理与流体微团所受作用之间的关系仍有待进一步研究。

本文利用PIV系统对槽道湍流流向-展向平面内的条带结构进行试验测量，采用本征正交分解方法提取和分离不同尺度的含能结构，采用流场中速度矢量组合象限分析方法研究了流体微团所受作用与条带结构变化之间的关系。

图1 PIV测试系统

1 试验系统

PIV测试系统如图1所示。图中x、y、z分别为流动的流向、法向和展向。该系统主要包括：双YAG激光器、激光器电源、导光臂、片光透镜组、同步触发器、CCD跨帧相机和计算机等，测量误差小于2%。试验在低速水槽中进行，所用示踪粒子是空心玻璃珠，平均公称直径为20滋m，在水槽中均匀布撒，粒子密度与水的密度接近，对流场有较好的跟随性。用激光片光照亮观测区域，用CCD跨帧相机拍摄并记录流场示踪粒子散射光信息。激光脉冲能量为300 mJ，波长为532 nm，相机分辨率为2048×2048像素，试验拍摄区域为100 mm×100 mm，流场空间分辨率为0.05 mm，粒子图像测速采集频率为7.4 Hz。试验拍摄流场通过自适应相关算法计算得到速度矢量场，查询窗口为32×32，重叠区为50%。水槽中自由来流速度为0.1 m/s，壁面摩擦速度为5.2 mm/s。通过对测量系统进行误差分析得知速度误差小于1.3%。

2 不同尺度流动结构分离

在近壁湍流中条带结构包括弯曲型和肿胀型。弯曲条带表现为条带结构沿流向周期性弯曲振荡，肿胀型条带表现为条带沿流向自身的膨胀和收缩。由于湍流流动结构具有多尺度特性，将不同尺度结构分离可以进一步研究其结构特性。Lumley[15]将本征正交分解方法引入湍流研究中，在随机流动的样本中找出1组能够最优捕获流动能量的基函数，将基函数按照其所含能量大小降序排列，低阶模态占有最多的能量，随着模态增加，其含能依次降低。随着试验技术的快速发展，由最开始的单点测量发展到2维平面测量以及3维立体测量。海量的数据给湍流场的研究提供大量信息，同时也给直接POD方法计算带来挑战。流场测量点数据的增多，使得空间相关矩阵维数巨大，求解较为困难。在此基础上，Sirovich[16]对直接POD方法进行改进，提出快照POD方法。该方法大大降低了相关矩阵的维数，在处理复杂、精细流场时得以推广应用。该方法将流动中每个瞬时场视为随机过程的1次独立实现，通过分解，得到空间模态和时间系数。本征正交分解方法可以将不同含能结构与物理尺度相关联，在湍流流动中广泛应用[17-19]。本文利用该方法将流动中不同尺度的流动结构分离。假设流动中1个快照所含速度信息为u（X，t），将N个快照排列在1个矩阵U中，其中X为空间点信息，t为时间序列。对矩阵U求得自相关矩阵A为

式中：UT为矩阵U的转置。

对自相关矩阵A求特征值和特征向量

式中：λi为特征值；bi为对应的特征向量。

将特征向量标准化可以得到POD的模态

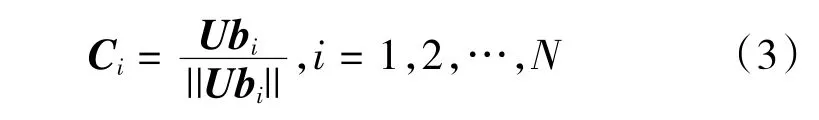
式中：Ci为第i阶模态；N为样本数。

得到不同尺度流动模态结构后，可以对模态场中流体微团速度分量进行象限分析[19-20]。定义（u'>0，w'>0）为第 1 象限，（u'<0， w'>0）为第 2 象限，（u'<0，w'<0）为第 3 象限，（u'>0，w'<0）为第 4 象限，并分别记为Q1、Q2、Q3、Q4，其中 u'为流向脉动速度，w'为展向脉动速度遥在流体微团中，如果流体的速度矢量为Q1和Q4组合或Q2和Q3组合，则该矢量组合为肿胀分布，表现为促进条带结构肿胀发展遥如果两侧速度矢量为Q1和Q2组合，或Q3和Q4组合，则该矢量组合为弯曲分布，表现为促进条带弯曲发展遥除了肿胀分布和弯曲分布之外，如果两侧速度矢量为Q1和 Q3组合或Q2和Q4组合，则该矢量组合为旋转分布，表现为促进条带结构的旋转遥上述组合方式如图2所示。

图2 不同象限事件组合

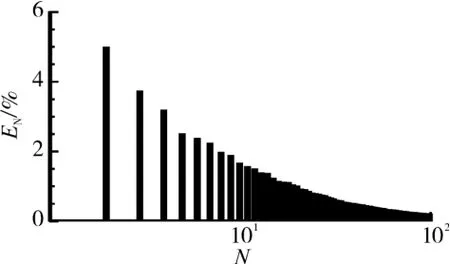
图3 模态含能变化

3 结果分析

本征正交分解得到的前100阶模态能量的分数变化如图3所示。从图中可见，低阶模态中流动结构含能较高，对湍动能贡献相对较大；随着模态数增加，模态含能迅速减小，对湍动能贡献较小。

本征正交分解得到的模态1、7和15，分别用来代表流动中的中大尺度结构，如图4所示。从图4（a）中可见，模态1流动结构尺度最大，条带结构呈现长直条状。条带结构中流体微团的速度矢量组合分布符合肿胀型分布，如图中白色椭圆所示。模态1中条带结构较为稳定，所含能量占湍动能百分比最大，约为6%。同时，注意到条带间流体微团的速度矢量组合分布模式为弯曲型分布，如图中黑色椭圆所示。在这种分布模式下，流体微团受到剪切作用。由于肿胀条带自身沿流向存在发散或收敛的变化，导致条带间流体微团的剪切作用沿流向分布不均匀，使条带将会发生弯曲。

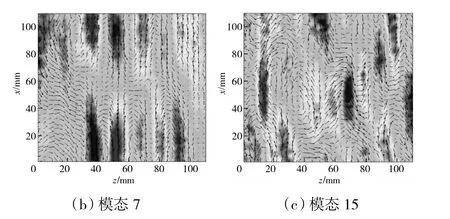
图4 不同象限事件组合

从图4（b）中可见，条带结构流向尺度大幅减小，同时条带数量显著增加，该模态中结构含能占湍动能百分比约为2.2%。在不同条带之间流体微团的速度矢量组合分布中，弯曲型组合分布显著增加，如图中黑色椭圆所示。由于条带流向尺度显著减小，弯曲作用增加，条带结构将出现碰撞、破碎和融合等多种变化。当符号相同的条带碰撞时，该处流体微团的矢量分布模式与肿胀型条带中心处矢量分布模式相同，可能诱使碰撞的条带发生汇聚，形成新的较大的肿胀型条带。当符号不相同的条带碰撞时，该处流体微团会出现较强的剪切作用，使条带沿展向倾斜并发生弯曲，可能转变为弯曲型条带。

随着模态数增加，模态中结构尺度进一步减小。从图4（c）中可见，模态15含能约为1.2%，出现了结构比较完整的法向涡漩结构，如图中黑色圆圈所示。该涡漩结构处的流体微团矢量组合分布为旋转分布，该结构在近壁面区域中流动尺度较小，相比于肿胀型或弯曲型条带，所含能量也较低。因此，在湍流流动的流向-展向平面内，肿胀型条带和弯曲型条带对湍动能的贡献占主要地位。