建立余热回收中纳米工质的导热系数预测模型

周树光，翟玉玲，王 江

(1. 国家能源集团云南阳宗海发电有限公司，云南 昆明 652103)(2.昆明理工大学 省部共建复杂有色金属重点实验室，冶金与能源学院，云南 昆明 650093)

随着全球能源危机的加剧，提高能源效率越来越受到研究者的关注。在工业生产过程中，经常产生废气或液体，其中含有大量热能、压力能或可燃成分[1]。多年来，为了达到最高的总能源效率和降低运行成本，人们采用了许多技术和方法来提高废热资源的利用率。在其他工业应用中也有大量的余热，如水泥厂、酸厂、发电厂等[2]。Le等[3]指出大约有27.9%世界最终消费总额的27.9%来自工业部门。例如，在水泥厂，水泥生产过程中约40%的能源消耗以余热的形式转移到环境中。此外，在制酸行业中，由于余热特点，在SO3冷却器及吸酸冷却器中存在大量温度波动的中低温余热可回收利用。

余热的回收率受工质热物性能的影响，传统的工质如水、工程油及乙二醇等导向系数比较低。因此，提出Choi[4]提出可在纳米级(尺寸小于100 nm)颗粒按合适的方法分散至液体中形成的胶体悬浮液。从成分上来说，它是一种纳米颗粒和液体共同组成的一种稀释悬浮液。与传统的冷却液体(如水、煤油、乙二醇和微流体等)相比，纳米流体已经显示表现出更高的热导率[5]。在实际应用过程中，有时需要流体同时具备几种性质，如既要稳定性好、又要导热性能高，甚至还需流变性能优异。混合纳米流体由于同时添加了几种不同性质的纳米粒子有可能全部满足这些要求[6]。Nabil等[7]指出陶瓷纳米颗粒如Al2O3粒子稳定性和化学惰性很好，但导热系数较低；而金属纳米颗粒导热系数高但容易氧化。若把二者混合，其混合纳米流体的稳定性既好又可同时提高导热系数。另一方面，由于粒子间的协同作用，相同浓度下其导热系数增幅明显高于单一纳米流体的。

基液的性质也会影响纳米流体的热物性，进而影响系统的换热量。Timofeeva等[8]和Maïga等[9]均发现乙二醇基液的导热系数增幅大于水的。Chiam等[10]指出乙二醇-水基液的热物性随着乙二醇含量及温度的变化明显。这一特殊性质非常适合应用于回收具有温度波动的余热中，但是关于含乙二醇-水基液的纳米流体的研究非常少。

此外，由于影响纳米流体导热系数的因素至今尚未完全明确，如温度、质量分数及混合比等因素之间并不是简单独立的，而是存在一种复杂的耦合关系。因此，本文以Cu/Al2O3-H2O/EG混合纳米流体为研究对象，研究基液混合比对导热系数影响，然后基于多项式回归理论提出导热系数的预测模型，用于指导纳米流体的工程应用。

1 实验过程

实验中用到的材料为：铜纳米颗粒，粒径50 nm，密度8.9 g/cm3，纯度99.9%；氧化铝纳米颗，粒径20 nm，密度3.5 g/cm3，纯度99.9%；乙二醇(EG)，密度1.115 5 g/cm3，纯度99%；去离子水(H2O)，密度1 g/cm3。

将H2O与EG按不同体积比混合，采用两步法制备Cu/Al2O3- H2O /EG混合纳米流体，研究基液比对混合纳米流体热物性的影响。纳米流体的具体制备过程如图1所示。实验研究质量分数为1%的Cu/Al2O3-H2O/EG混合纳米流体，制备不同基液体积比(基液比)H2O∶EG(80∶20、60∶40、50∶50、40∶60、20∶80)的纳米流体共5组。其中纳米铜颗粒与纳米氧化铝颗粒质量比为50∶50。每组配制50 g的纳米流体，其中纳米铜与纳米氧化铝各0.25 g，基液总质量49.5 g。目的是分析对比各组纳米流体的综合性能，得到稳定性较好、导热系数较高、黏度较低的纳米流体。

图2为Cu/Al2O3-W/EG混合纳米流体在初始制备时不同基液比下的TEM图。如图2所示，近似圆形的深色大颗粒为Cu粒子(50 nm)，近似棒状、块状的浅色小颗粒为Al2O3粒子(20 nm)，通过粒子密集程度可看出其分散性。由图2可发现纳米流体基液中EG含量越多，其团聚体越少，粒子的分散越均匀，且团聚体尺寸较小。同时通过TEM图可发现，Cu/Al2O3-H2O/EG混合纳米流体粒子的团聚通常是Cu粒子与Cu粒子、Al2O3粒子与Al2O3粒子的结合团聚，而Cu粒子与Al2O3粒子的团聚体则较少。可能是粒子间不同吸附力造成的，需进一步实验验证。

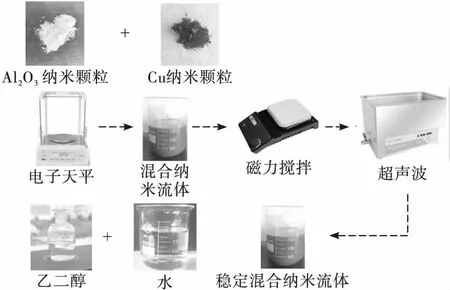
图1 Cu/Al2O3-H2O/EG混合纳米流体制备流程

图2 不同基液比下Cu/Al2O3-H2O/EG混合纳米流体TEM图

2 多项式回归预测模型

有关纳米流体导热系数的经验模型Maxwell[11]以早期颗粒悬浮体系提出了球形固体颗粒悬浮在液体中的公式模型：

(1)

式中：keff，kp及kbf分别为悬浮体系、固体颗粒及基液的导热系数，W/(m·K)-1；φ为固体颗粒体积分数，%。

Hamilton和Crosser[12]在Maxwell模型基础上加入颗粒形状的因素影响，提出了新的导热系数公式模型(见图3，简称HC模型)：

(2)

式中：n为形状因子，n=3/Φ，Φ为固体颗粒球形度，表示固体颗粒形状接近球形的程度。

Lu等[13]提出了适用于球形固体颗粒的两相悬浮液导热系数公式模型：

(3)

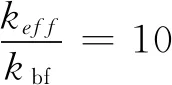
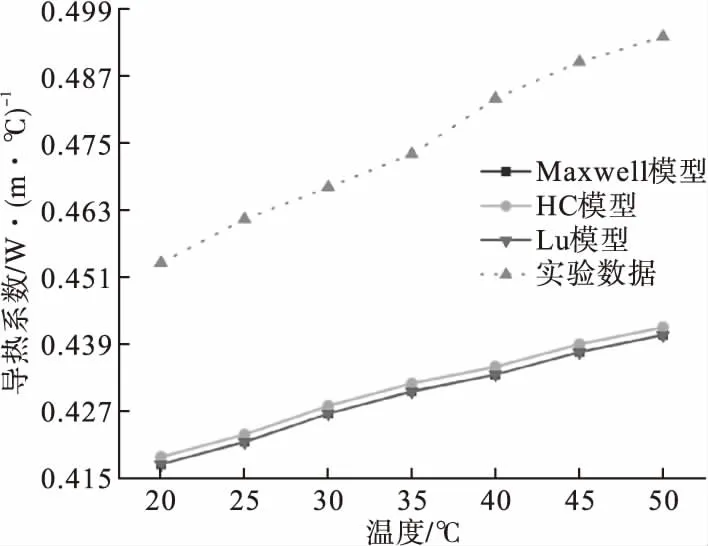
图3 三组导热系数模型与实验数据对比图

在已知基液导热系数情况下以基液比60∶40为例，将上述三组模型与实验数据进行对比，如图3所示。从图3可以看到，Maxwell模型与Lu模型数据相差较小，而以上三种模型与实验数据误差很大。因现有纳米流体导热系数理论模型适用条件均为单种粒子，本文中纳米流体粒子为混合粒子。

在纳米流体导热系数预测中，往往很难给出一个确切的回归方程。在不能确切给定回归方程时，通常用多项式方程作为回归方程[14]。这在理论上是可行的，因为任何曲线都可以用多项式来逼近[15]。对于纳米流体导热系数而言，作为一种有效的数据分析方法，多项式回归是一种特殊的多元线性回归方法，能够通过统计发现不同变量之间的相关关系，实现定量表征。多元线性回归(MLR)尝试通过已知数据找到一个线性方程来描述两个及以上的特征(自变量)与输出(因变量)之间的关系，并用这个线性方程来预测结果。多元线性回归的数学模型如下：

y=b0+b1x1+b2x2…+bnxn+ut

(4)

式中：ut(t=1,2,…,n)为随机项误差。

在多元线性回归过程中，均方误差是比较常用的一个损失函数，回归分析的目的就是要基于均方误差最小化来对模型的参数进行求解，损失函数的形式为

(5)

式中：y为样本真实值，f(x)为神经网络期望值，t为样本数目。

假设上述回归模型已通过回归方程显著性检验和回归系数显著性检验能够应用于实际问题。则对于给定观测点x0=(x01,x02,…,x0p)T，可以采用下式进行预测。

y0=β0+β1x01+...+βpx0p+ε0

(6)

误差ε0是一个随机变量，均值为0，ε0的方差对于所有的自变量来说相等，所有ε0的值是独立的，ε0满足正态分布，反映y0的期望值。

3 结果分析与讨论

图4为不同基液比下Cu/Al2O3-H2O/EG混合纳米流体导热系数随温度的变化。由图4可知，纳米流体的导热系数随着温度的升高而非线性增大。当温度从20℃升至50℃，导热系数增幅(λ50℃-λ20℃)最小(基液比20∶80)为0.020 9 W/(m·K)-1，最大(基液比80∶20)为0.053 3 W/(m·K)-1。这是因为在基液中，温度升高时，液体分子的不规则运动加剧，分子间碰撞加剧，因分子在碰撞的同时伴随着热量交换，故分子间的热量交换频率加剧，故导热系数增加。而在Cu/Al2O3-H2O/EG混合纳米流体中，温度升高时不仅有基液分子的碰撞频率加剧，同时存在着纳米粒子受流体分子影响而产生的布朗运动加剧，其结果便是纳米粒子间的碰撞便频繁，粒子与基液分子的换热加快，故宏观表现为导热系数增加[16]。

由前面分析可知，混合纳米流体导热系数受粒子和基液种类、温度及混合比等影响很大，且变化规律呈非线性变化。因此，首先采用多项式回归分析方法对Cu/Al2O3-H2O/EG混合纳米流体导热系数的实验数据进行回归分析，得到以下回归方程：

keff=0.257 3+0.152 8Rm+0.000 3T+0.163 1Rm2+0.001 6RmT

(7)

该方程适用范围：Cu/Al2O3-H2O/EG混合纳米流体，质量分数w：1%，温度T：20～50℃，混合比R：0∶100～100∶0。该回归方程多元统计系数R2为0.998 40。R2越接近1，说明预测结果较为精确。

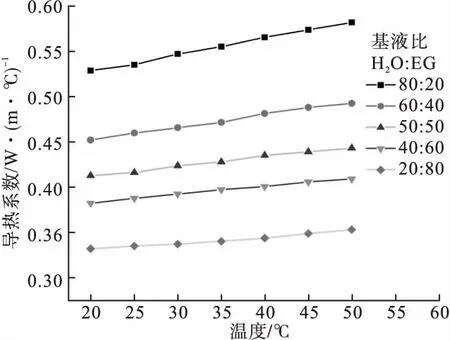
图4 Cu/Al2O3-H2O/EG混合纳米流体在不同基液比(H2O∶EG)下导热系数与温度的关系

图5为实验数据在多项式回归导热系数模型的三维图分布图。由图可发现，Cu/Al2O3-H2O/EG混合纳米流体在不同去离子水在基液中所占比例下的导热系数随温度变化很有规律。图5中数值点大部分在三维曲面上且相关系数R2=0.998，说明该公式拟合的比较准确。

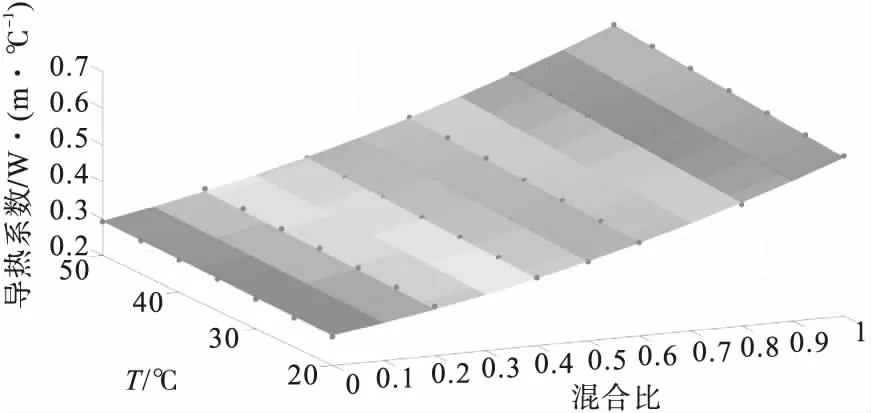
图5 导热系数预测值及实验值随基液比和温度的变化

图6为多项式回归的导热系数残差图。残差是指实际值与预测值的差。残差分析是依靠残差的所表示的信息，分析预测模型的准确程度。按照某种标准取一个阀值来限定异常点，若某个点的残差大于阀值，便可认为它是异常点。残差图是指以残差为纵坐标，以其他设定的量为横坐标的散点图。可用来检查回归线中的异常点[17]。从图6可以看到，仅存在两个异常点，这说明导热系数与黏度的多项式回归方程拟合较为准确。

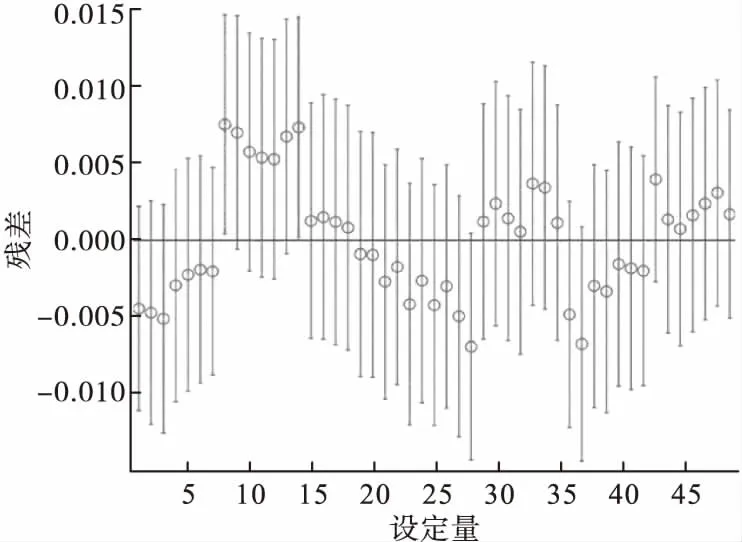
图6 导热系数残差图

4 结 论

采用两步法制备质量分数为1%的Cu/Al2O3-H2O/EG混合纳米流体，基液混合比分别为80∶20、60∶40、50∶50、40∶60、20∶80，研究其导热系数随温度和基液混合比的变化情况。然后，根据多项式回归理论拟合Cu/Al2O3-H2O/EG混合纳米流体的导热系数预测模型。得到了以下主要结论：

(1)对比分析TEM图，纳米流体基液中EG含量越多，其团聚体越少，粒子的分散越均匀，且团聚体尺寸较小。由于不同种类粒子间的分子吸附力不同，导致Cu粒子与Cu粒子、Al2O3粒子与Al2O3粒子的结合团聚，而Cu粒子与Al2O3粒子的团聚体则较少。

(2)导热系数随着温度的升高非线性升高，随基液中水含量的增大而下降。

(3)根据实验数据，拟合了导热系数与温度及基液混合比的多项式预测模型，R2达0.998，精度较高可以很好地预测Cu/Al2O3-H2O/EG混合纳米流体的导热系数。