基于灰狼算法和极大似然估计的改进DV-HOP算法

朱晓娟 陈智丽

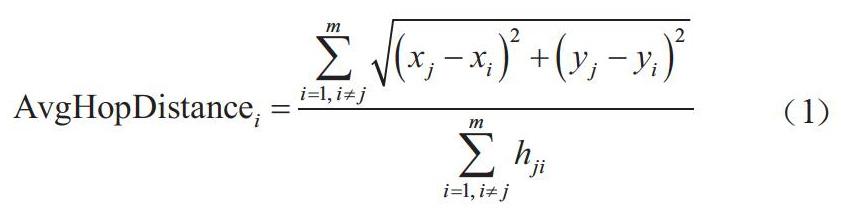
摘 要：DV-HOP算法是无线传感器网络中一种常见的基于非测距的定位技术，该算法使用平均跳距表示实际距离，在实际应用中造成很大的误差和节点能耗。为此，在原有DV-HOP算法的基础上，引入了灰狼算法细化节点之间的跳数，用极大似然估计法修正实际坐标与估计坐标之间的误差。仿真结果表明，改进算法在不显著提高算法复杂度的基础上提高了一定的定位精度。

关键词：无线传感器网络;DV-HOP算法;灰狼算法;极大似然估计;误差分析;平均跳跃距离

中图分类号：TP39 文献标识码：A 文章编号：2095-1302（2020）05-00-05

0 引 言

随着无线网络的高速发展，无线定位技术受到了业界的广泛关注，已经在智能农业[1]、目标跟踪[2]、水质监测[3]、远程医疗[4]等领域得到不断发展。在无线传感器网络的大多数应用中，没有位置信息的任何事件信息都是毫无意义的。例如，在火灾探测应用程序中，需要事件（火灾）和探测火灾的地点（位置）。因此，精准定位是无线传感器网络的要求。

定位的基本方法分为距离式定位和非距离式定位。距离式定位[5]是通过测量距离或角度进行位置估计，测量数据的精度对定位精度有很大影响，常见的基于距离的定位算法有RSSI，AOA，TOA，TDOA[6]等。非距离式定位[5]是通过节点间的HOP数或估计距离计算节点的坐标，这种方法无需测量距离或角度，利用估计距离代替真实距离，常见的非距离式定位算法有CL，DV-HOP，APIT等。其中，DV-HOP算法不仅开销低，还可以处理普通节点少于3个相邻锚点的情况。国内外许多学者对DV-HOP算法提出了改进，使得定位精度大大提高。例如，AMANPREET KAUR提出了一种加权质心DV-HOP算法[7]，该算法考虑不同因素（如锚数、通信半径和最近锚）影响的权重来确定未知节点的位置。Guangshun Li对传统的DV-HOP算法[8]提出了两方面的改进：对平均每条跳距进行修正;分别采用加权质心定位算法和加权最小二乘法分别得到一个估计位置，并由2个估计位置的算术均值确定最终位置。XUE Dalong提出了一种基于跳变细化和距离校正的改进型DV-HOP算法[9]。通过引入接收信号强度指示（RSSI）测距技术来校正最小跳，通过跳跃距离误差和估计距离误差的加权平均值对平均跳跃距离进行校正。LIU Guiqi等人[10]提出了一种基于跳的校正平均大小改进的DV-HOP定位算法，改进的算法根据跳数信息和锚节点信息的相对准确的坐标来校正未知节点与不同锚节点之间的估计距离，并使用改进的差分进化算法获得未知节点的估计位置。本文提出了一种基于多通道半径和极大似然估计的改进DV-HOP算法，在原有DV-HOP算法的基础上，引入了多通道半径广播细化节点之间的跳数，用极大似然估计法修正实际坐标与估计坐标之间的误差。仿真结果表明，相比较传统的DV-HOP算法，本文算法在定位精度上有一定提高。

1 DV-HOP算法与误差分析

1.1 传统的DV-HOP算法

DV-HOP（Distance Vector-Hop）算法是由美国Rutgers University的Dragons等人提出的。该算法使用路由交换协议使未知节点获得锚节点信息，并用于计算其自身坐标。DV-HOP算法主要由三个阶段组成[7]。

（1）获取锚节点和未知节点的跳数信息

通过可控的泛洪算法，网络中的锚节点将其位置数据包广播到整个网络。接收到来自锚节点的信息后，邻居节点会将数据包中的跃点值增加一跳，然后将其转发到下一个邻居节点。接收节点只保留来自同一锚节点的最小跳数信息，忽略较大跳数的信息包。泛洪后，所有节点将获得每个锚节点的最小路径和跳值。

（2）计算锚节点之间的平均跳跃距离

令锚节点i与其他锚节点j之间的平均跳距为AvgHopdistance。通过公式（1）估算自身平均跳距：

式中：m是给定网络中的锚的总数;i是每个锚的id;（xi， yi）和（xj， yj）分别为锚节点i和锚节点j的坐标;hji是锚节点i和锚节点j之间的最小跳数。

每个未知节点u使用式（2）计算距锚节点i的近似距离。其中，hui是锚节点i和未知节点u之間的最小跳数。

（3）确定未知节点的坐标

当获得未知节点与三个或者更多锚节点之间的距离时，可以用最小二乘法来求解自身坐标。

利用未知节点u和锚节点i的坐标（xu， yu）和（xi， xj）可以得到方程（3）：

化简后可得方程（4）：

方程（4）可写成Ax=B的形式：

由此可得未知节点u的坐标为Xu=（ATA）-1ATB

1.2 DV-HOP算法的误差分析

在实际应用中，由于信标节点的成本较高，所以并不会大面积部署。此外，实际布置节点是随机的，无法保证分布的合理性。所以，DV-HOP算法在实际应用中精度必定存在一定误差。

由于在实际应用中，节点随机且不均匀地部署在给定监视区域中。因此，对于锚节点而言，其通信半径中存在许多未知节点，并且未知节点与锚节点之间的距离并不完全相等。但是DV-HOP算法在计算它们之间的距离时，获得的结果一致。

在DV-HOP算法中，用信标节点的跳数乘以平均每跳的距离来表示节点之间的距离，这种估算方法可能会存在较大误差。例如图1所示的网络拓扑结构。

图1中，A1，A2，A3为信标节点，其余的为未知节点。A1，A2之间的距离为20 m，A2，A3之间的距离为40 m，由式（1）可得AvgHopDistance =7.5。然而由于各节点之间的距离不同，所以计算出来的平均每跳距离与实际相比存在误差，跳数越多，累计误差越大。

2 算法的改进

2.1 标准灰狼优化算法

GWO算法由Mirjalili等人提出，它是受到灰狼狩猎机制启发而出现的一种元启发式优化技术，该算法简单、灵活。文献[12]与其他知名的优化算法进行了28种基准测试功能的比较，证明了GWO优于其他元启发式优化算法。

灰狼主要为群居方式生活，并且等级制度严明。灰狼一般分成四类：头狼称为α，它是领导者，主要负责群体中的各项事务，包括选择追逐、休息的地点，唤醒时间等;略次于α的称为β，它作为α的下属，负责辅助α对群体进行管理决策;次于β的称为σ，它听从α和β的指令，但能指挥更底层的个体，负责执行侦查、看护、放哨等任务，年迈的α和β也会降为σ;最底层的称为ω，它们主要负责捕猎[13]。

在GWO算法中，α，β和σ分别表示为最优解、次优解和第三最优解，其他个体为ω，猎物的最终位置即为所求未知节点的位置。

灰狼群接近猎物行为的数学模型分为种群初始化、种群搜索和种群位置更新三个过程。

2.1.1 种群初始化

该算法在运行之初需要将搜索个体分布到搜索区域中，采取随机布设方式，即：

式中：x为灰狼个体，i∈[1， 2， ...， N]，j∈[1， 2， ...， D];N是灰狼个体数量;D是种群的维数;lb和ub构成搜索区间的边界;R是随机分布函数。

2.1.2 种群搜索

灰狼个体与猎物之间的距离通过式（7）确定，灰狼个体按照公式（8）接近猎物：

式中：D为猎物与灰狼之间的距离;C和A为系数;Xp和X为猎物位置和个体位置。

系数C和A的计算公式如下：

式中：r1和r2是[0，1]之间任意一个数字;t为当前迭代次数;tmax为最大迭代次数。

2.1.3 种群位置信息计算

当狼群发现猎物后，假设α，β和σ为更好地了解猎物，提出下列公式以获取猎物的信息。通过式（12）、式（13）计算出个体与α，β和σ的距离，再由式（14）计算出猎物移动的方向：

2.2 灰狼算法修正平均跳數

在经典的DV-HOP第二阶段，信标节点通过应用式（1）计算平均跳距，然后应用式（3）计算它们与每个信标的距离。此后，信标使用灰狼算法细化平均跳距。式（15）为用于实现最佳平均跳跃距离的适应度函数：

此阶段可帮助所有信标获得精确的平均跳数。所有平均跳数都会广播给网络中的其他节点，然后再通过取最接近信标到给定节点的平均跳数与最小跳数的乘积来得出每个信标的距离。使用灰狼算法通过每个信标获得最佳平均跳数的步骤：

初始化随机数a，A，C，根据式（16）寻找目标fobj，fobβ，fobσ，设置Xα，Xβ，Xσ的初始最佳估计，在该算法中，Xα被设定为由给定信标计算的平均跳数，Xβ和Xσ被设定为所有信标计算的平均跳数。算法如下：

初始化i=1

do

for 每一个节点用式（15）更新其平均跳数

end for

更新a，A，C的值，再次决定目标函数fobj1

If fobj1

用新值更新Xα且fobjβ=fobj1

else

if fobj1>fobj and fobj1

用新值更新Xβ且fobjβ=fobj1

end if

else

if fobj1>fobj and fobj>fobjβ and fobj1

用新值更新Xσ且fobjσ=fobj1

End if

else

清空fobj1的值，保持先前的fobj

end if

用式（13）更新Xα，Xβ和Xσ

I=i+1

end for

得到Xα，Xβ，Xσ的质心，返回最优平均跳数

2.3 极大似然估计法修正坐标

在式（4）的求解过程中，用每个方程与最后一个方程作差得到修正值。虽然使方程更加简洁明了，但是相减还是会丢失一部分信息，从而导致计算误差。为了减少计算误差，可以对方程进行泰勒公式展开。对于式（3），令

偏差量（Δx， Δy）表示实际位置（x， y）与估计位置  的差值，即，所以式（17）可改写成：

f （x， y） 在  处的泰勒展开为：

将式（19）中一阶偏导之后的展开项省略，以避免式中非线性项的干扰。对f （x， y）在  求一阶偏导为：

式（19）可以表示为：

令

则式（22）可以表示为，即：

令

所以方程组可表示为AX=B，根据最小二乘式可得到X=（ATA）-1ATB。然后可得未知节点的坐标，偏差量（Δx， Δy） 的值决定了定位的精度。

3 实验仿真验证

3.1 仿真环境

为了验证改进后算法的精确性，采用Matlab 2018a进行仿真。仿真环境为100 m×100 m的正方形区域，区域中随机分布有100个节点。在锚节点数相同的情况下，进行多次实验取平均值。本文选取未知节点平均相对定位误差作为评价指标，表示为：

式中：N为节点总数;n为信标节点数;R为节点的通信半径;（xi， yi）和（Xi， Yi）分别为未知节点i的估计坐标和真实坐标。

仿真参数见表1所列。

节点随机分布如图2所示。

3.2 仿真结果分析

3.2.1 节点总数对定位性能的影响

当通信半径为30 m，信标节点比例保持在30%时，调整节点总数进行仿真。如图3所示，随着节点总数的增加，进行测试的3个算法的平均误差都在逐渐降低。这是因为随着总节点的增加，节点之间的密度增大，从而降低了节点之间的距离，使得跳数和平均跳距估计更加准确。由图可知，本文算法的平均误差较小。

3.2.2 通信半径对定位性能的影响

通信半径的大小决定了未知节点可以获得的信标节点的数量。图4表示节点总数为100，信标节点为10个，通信半径由20 m变化为40 m时经典DV-HOP算法、文献[7]的算法、文献[8]的算法以及本文改进算法的平均定位误差仿真图。由图3的仿真结果可以看出，通信半径的增大有效降低了节点的相对平均误差，本文提出的改进算法相较于比对算法，平均相对误差有一定的降低。但是通信半径并非越大越好，通信半径越大能耗就越多。

4 结 语

本文提出了基于极大似然估计法的DV-HOP改进算法，在经典算法的基础上细化节点之间的跳数值，同时采用极大似然估计法修正求解节点坐标时产生的误差。通过Matlab仿真实验，与经典的DV-HOP算法和其他两种算法进行对比，充分验证了本文算法能够在一定程度上减少定位误差，提高定位精度。

参考文献

[1] Ban?ur，?oko Jak?i?，Branimir Ban?ur，et al. An analysis of energy efficiency in wireless sensor networks（WSNs）applied in smart agriculture [J]. Computers and electronics in agriculture，2019，156：500-507.

[2] JERWIN PRABU.Optimization approach for a climbing robot with target tracking in WSNs [J]. Journal of ocean engineering and science，2018，3（4）：282-287.

[3] Design a WSN system for monitoring the safety of drinking water quality [J]. IFAC-papers on line，2018，51（17）：752-757.

[4] An improved three-factor authentication scheme for patient monitoring using WSN in remote health-care system [J]. Computer methods and programs in biomedicine，2019，182.

[5]郝志凱，王硕.无线传感器网络定位方法综述[J].华中科技大学学报（自然科学版），2008（S1）：224-227.

[6]景路路，张玲华.基于跳距优化的改进型DV-HOP定位算法[J].传感技术学报，2017，30（4）：582-586.

[7] AMANPREET KAUR，PADAM KUMAR，GOVIND P GUPTA. A weighted centroid localization algorithm for randomly deployed wireless sensor networks [J]. Journal of king saud university - computer and information sciences，2019，39（1）：82-91.

[8] DV-Hop localization algorithm based on minimum mean square error in internet of things [J]. Procedia computer science，2019，147：458-462.

[9] XUE D L. Research of localization algorithm for wireless sensor network based on DV-Hop [J]. Eurasip journal on wireless communications an networking，2019（1）.

[10] LIU G Q，QIAN Z H，WANG X. An Improved DV-HOP localization algorithm based on HOP distances correction [J].中国通信，2019，16（6）：200-214.

[11]张晓凤，王秀英.灰狼优化算法研究综述[J].计算机科学，2019，46（3）：30-38.

[12] MIRJALILI S，MIRJALILI S M，LEWIS A. Advances in engineering software [J]. Grey wolf optimizer，2014，69：46-61.

[13] LONG W，ZHAO D Q，XU S J. Improved grey wolf optimization algorithm for constrained optimization problem [J]. Journal of computer applications，2015，35（9）：2590-2592.