农田土壤含水率空间变异的时变特性研究

2020-06-11王仰仁

节水灌溉 2020年3期

姚丽，王仰仁，陈钊，高微，张喆

(1.天津农学院水利工程学院，天津 300384；2.天津市节水灌溉技术与装备校企协同创新实验室，天津 300384；3.天津市武清区水利技术推广中心，天津 301700)

0 引言

农田土壤水分随空间点变化呈现随机性，即在同样地块、同样灌水时间不同空间点土壤含水率不相同，而且，土壤水分的空间变异随时间是变化的，将此称为土壤水分的时空变异。土壤水分时空变异是由多重尺度上的土地利用(植被)、气象(降雨)、地形、土壤、人为活动等多因子综合作用的结果[1]。土壤含水率具有较强的空间变异性[2]，国内外学者对此有了较多的研究，研究的方法有多种，例如，经典统计学方法、地统计学方法、染色示踪法、时间序列法、土壤水分成像法等[3]。土壤水分时空变异也会随着尺度的变化而发生明显的改变, 大尺度由大气控制，主要决定于降雨和蒸发格局, 小尺度主要决定于土壤、地形、植被和根系结构等[4]。高科认为黄河源区的土壤水分整体在弱变异性范围内，林地覆盖下土壤含水率变异系数最高[5]；窦旭以河套灌区下游乌拉特灌域为研究区，对盐渍化灌区土壤水分空间变异性进行了研究，认为表层土壤含水率变异系数较高，属于中等变异范围，深层土壤含水率变异系数较低，属于弱变异范围[6]。纵观现有研究，对农田尺度土壤水分空间变异性研究多局限于短时段的、基于人工测试的土壤墒情，对于土壤含水率空间变异随时间变化特性研究还较少。本文以TDR式土壤墒情传感器监测的土壤含水率为依据，利用经典统计学方法，研究了农田尺度空间变异随时间的变化，目标是为农田精准灌溉提供依据。

1 材料与方法

1.1 试区概况

试验于天津市武清区北靳庄试验区(117°1′E，39°22′N，海拔8 m)，属暖温带半湿润大陆性季风气候。年平均气温为11.6 ℃，1月平均气温为-5.1 ℃，7月平均气温为26.1 ℃，年平均降水量为606 mm，土壤为中壤土，土质疏松肥沃，宜于农业生产，该地区有较好的灌溉条件，水源从永定新河引入沟渠，再提水灌溉，小麦生育期一般灌水2～3次，玉米生育期灌水一般1～2次，全村耕地154．67 hm2。该地区多年平均气温12.2℃，多年平均降雨量为557.3 mm 左右，蒸发量1 735.9 mm。土壤质地为中轻壤土，0～100 cm 土壤平均干容重1.41 g/cm3，田间持水率24.6%，地下水埋深随季节变化而有所变化，干旱季节4～5 m，雨季1～2 m。试点分层土壤水分特征参数值见表1。

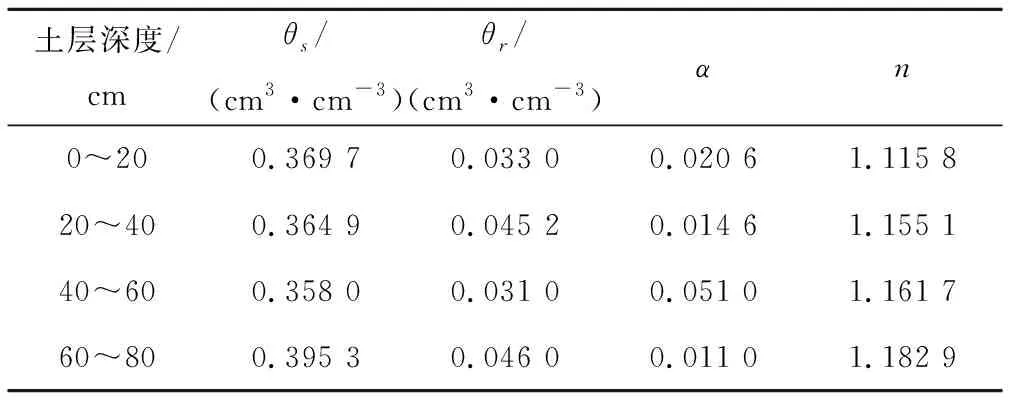
表1 试点分层土壤水分特征参数Tab.1 Pilot layered soil moisture characteristic parameters

1.2 试验方法

本试区两套墒情监测系统分别设置于天津市武清区崔黄口镇北靳庄试区和西吕村试区，用于监测大田土壤墒情，系统布置见图1，试区面积286.67 hm2。传感器采集的土壤含水率(体积含水率)数据为小时值，数据管理中心设置在天津农学院水利工程学院。每套系统有一个基站，基站控制3个测点(B1、B2、B3代表北靳庄第一个、第二个、第三个测点的土壤含水率，X1、X2、X3代表西吕村第一个、第二个、第三个测点的土壤含水率)。每个测点连接两个土壤水分传感器(埋设于地表下30和60 cm处)，其中有一个测点埋设地温传感器(埋设于地表下30 cm处)。两台基站相距2 560 m；由于二者相距较近，仅在一个基站设置了天气信息(空气温湿度、有效光合辐射、降雨量)采集传感器。测点将土壤水分和温度传感器采集的数据实时无线发送到基站，基站再将采集的天气信息、测点传来的土壤水分和土壤温度信息通过互联网实时传输到数据管理中心。

图1 基站及节点分布图Fig.1 Base station and measuring point distribution map

1.3 分析方法

1.3.1 土壤剖面平均含水率的计算

传感器测得的为30、60 cm处土壤含水率，需转化为0～60 cm平均含水率作为土壤墒情。由于传感器监测到的是逐小时土壤含水率，现取每日中午12时的土壤含水率作为当日土壤含水率，得到逐日土壤含水率(30、60 cm)，时间为2017年11月7日至2019年8月29日，共660 d。利用式(1)求得0～60 cm土壤含水率。

xk(t)=a1xl(t)+b1xm(t)+c1(l、m、k=1,2,3,…,6)

(1)

式中：xl(t)为传感器监测的逐日30 cm处的含水率；xm(t)为传感器监测到的逐日60 cm处的含水率；xk(t)为逐日0～60 cm平均含水率；l、m、k表示试区测点的序号，根据李泳霖[7]的研究结果；a1为0.645；b1为0.264；c1为1.868。

1.3.2 变异系数的计算

经典统计学通常用变异系数(CV)的大小描述变量的变异程度，当CV≤10% 时为弱变异，当10%≤CV≤100% 时为中等变异，当CV≥100% 时为强变异[8]。按式(2)～(4)计算得6个节点的分层(30 cm和60 cm处)、平均土壤含水率(0～60 cm)随时间变化的CV值。

(2)

(3)

(4)

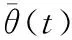
1.3.3 测点土壤含水率相关性分析

本研究以2个测点、3个测点土壤含水量的相关关系来描述不同距离测点土壤含水率的相关性。两个测点之间的相关系数按照式(5)计算，由此分析相关系数随测点之间距离的变化情况；3个测点之间的相关系数，则利用多元线性回归分析的方法确定，试区共6个测点，选取其中一个测点的土壤含水率作为因变量，从剩余的5个测点中选取两个作为自变量，按照式(6)做回归分析，可求得式中参数(a2、b2、c2)、相关系数[式(7)]和相对误差[式(8)和式(9)]。

(5)

(6)

(7)

(8)

(9)

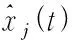
2 结果分析与讨论

2.1 监测点土壤含水率的变化过程

图2给出了由传感器测得的6个测点的土壤含水率以及按式(1)计算得到的0～60 cm土层平均含水率随时间的变化过程，图2中还给出了对应时间的降雨量。

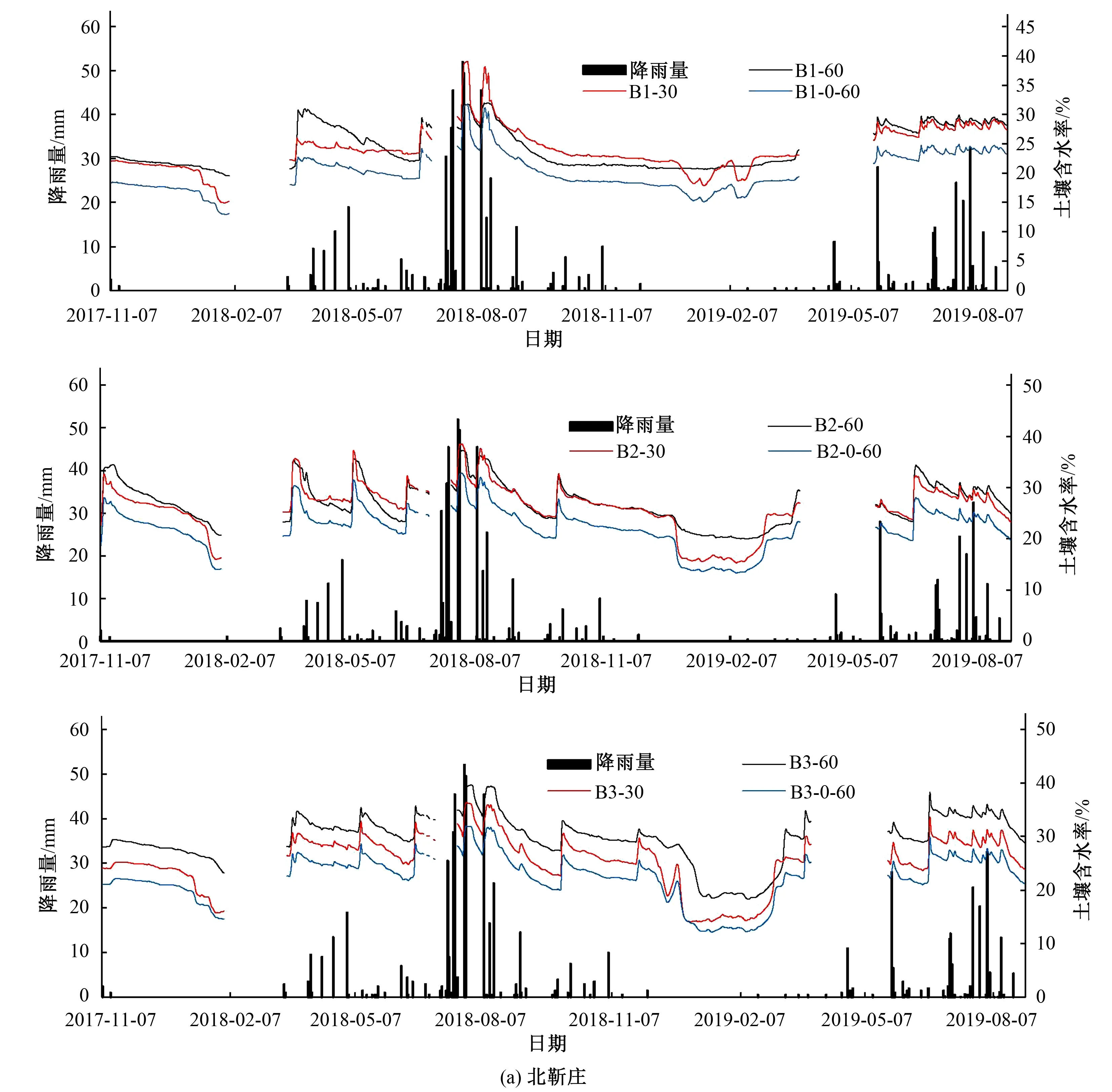
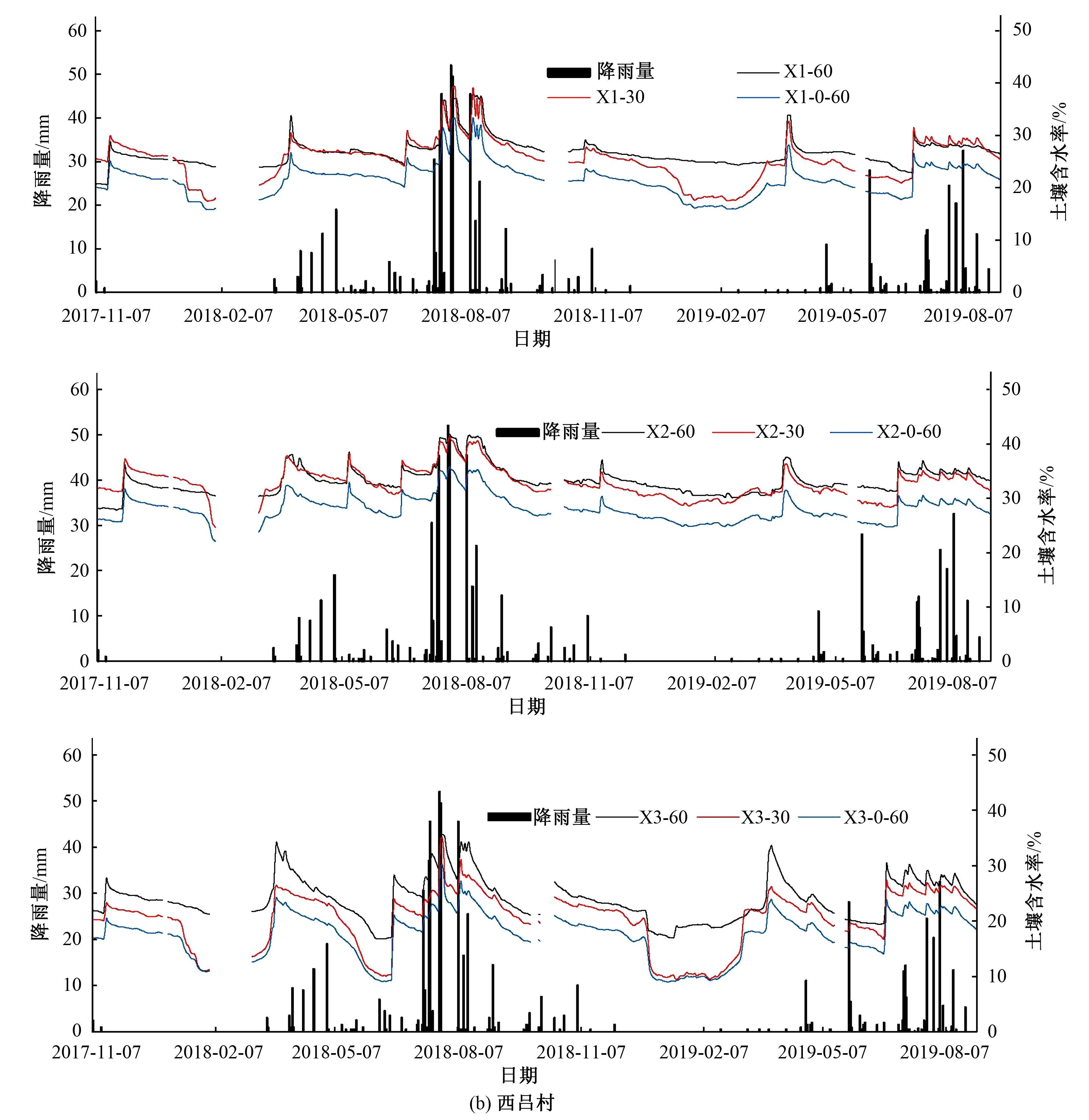
图2 北靳庄、西吕村监测点土壤含水率随时间变化过程Fig.2 Change of soil water content with time at monitoring points in Beijinzhuang and Xilv Village

从图2中可以看出，①土壤含水率有缺测情况，主要原因是传感器设备的故障问题；②30 cm处的土壤含水率的波动比较大，主要原因是表层土壤含水率变化较大；330 cm处土壤含水率普遍大于60 cm处的含水率；④土壤含水率有显著增大的时间点，该点处或者有较大降雨，或者有灌水。由此可确定测点所在地块的灌水时间和灌水次数，进而分析给出当地灌水情况。

从图2还可以看出，不同测点土壤含水率变化差异较大，有的测点含水率变化较大(西吕村测点3、北靳庄测点2和测点3)，有的测点含水率变化较为平缓(西吕村测点1、测点2和北靳庄测点1)，测点含水率变化较为平缓的情况下，土壤含水率往往较大，比如2018年7-8月、2019年7-8月期间，各测点土壤含水率变化均较为平缓，其最低含水率普遍在20%以上。

2.2 土壤含水率变异系数随时间的变化过程

通过计算，给出试区6个测点的土壤含水率的最大值、最小值、平均值以及变异系数的变化范围，见表2。6个测点30、60 cm处以及0～60 cm土壤含水率的最大值、最小值和平均值随时间的变化过程，见图3。

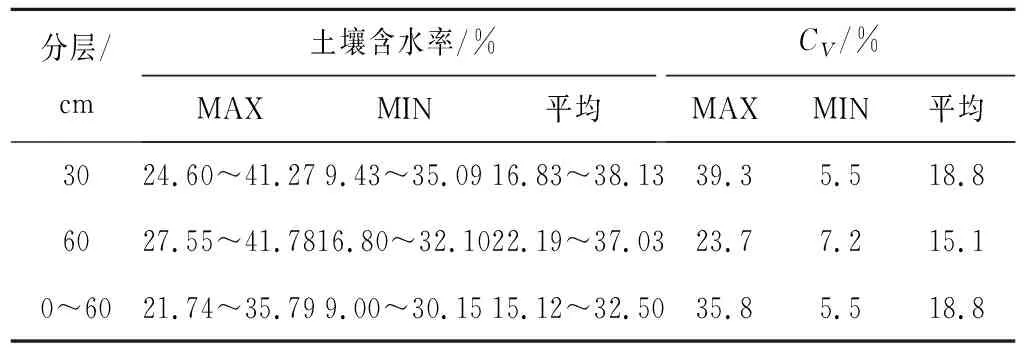
表2 土壤含水率最大值、最小值、平均值和变异系数的变化范围Tab.2 variation Range of soil moisture content maximum, minimum, average and coefficient of variation

从表2中可以看到，6个测点土壤含水率的最大值的变化范围为21.74%～41.78%，最小土壤含水率的变化范围为9.43%～35.09%。从表2可以看到，6个测点30 cm处土壤含水率变异系数的变化范围为5.5%～39.3%；60 cm处土壤含水率变异系数的变化范围为7.2%～23.7%，小于30 cm处土壤含水率变异系数的变化范围；0～60 cm平均土壤含水率变异系数的变化范围为5%～35.8%，均呈弱变异和中等变异。

从图3可以看出：

(1)各层逐日土壤含水率的差异较大，30、60、0～60 cm处土壤含水率变化幅度分别变化于4.7%～21.8%、6%～16%、4.4%～17.7%，30 cm处土壤含水率的变化幅度最大。

图3 土壤含水率最大值、最小值、CV随时间的变化过程Fig.3 The process of changing the maximum, minimum and CV of soil moisture content with time

(2)测试时期内30、60、0～60 cm土壤含水率的变异系数差异较大，如2017年12月至2018年3月、2018年5-6月、2019年5-6月、2018年12月至2019年3月土壤含水率的变异系数变化于15%～40%，该时期为灌溉期，土壤含水率较小(最小可达9%)。测试期间7-9月，土壤含水率的变异系数差异相对较小，变化于10%～20%，该时段为雨季，土壤含水率较大(均大于20%)。有学者研究结果与本研究这一结果一致，土壤含水率越高，土壤变异性越小[12-14]，但也有学者的研究结果为土壤含水率越大土壤变异性越大[9]，主要原因是该学者的研究尺度较小(0.25、0.01、0.000 4 hm2)。

(3)60 cm处土壤含水率的变异系数变化较稳定，相应的30 cm处变化幅度较大；0～60 cm平均土壤含水率的变异系数变化幅度与30 cm处的变化一致，30 cm和0～60 cm土壤含水率的变异系数普遍高于60 cm处的变异系数，表明土壤表层的含水率变化幅度较大。

2.3 测试点土壤含水率的相关关系

2.3.1 两个测点土壤含水率相关关系

对试区6个测点土壤含水率相关性进行分析，得到15组相关系数。以两个测点之间的距离为横坐标，相关系数为纵坐标，得到相关系数随距离的变化情况，见图4。

从图4中可以看到，一个基站控制的3个测点土壤含水率两两相关系数变化于0.702 5～0.932 7(30 cm)和0.636 0～0.838 5(60 cm)，30 cm处土壤含水率的相关系数与60 cm处的相关系数变化情况相近，随着距离的增大先增大再减小进而继续增大，相关系数最高可达0.932 7，均达到极显著水平[r=(500,0.01)=0.115，r(1 000,0.01)=0.081，500为样本数，0.01为显著性水平]因此可以说明在一定距离内一个点的土壤含水率在一定程度上可代表另外一个点的含水率；将两个基站控制的测点进行两两相关性分析，得到土壤含水率的相关系数变化范围为0.612 8～0.855 9(30 cm)和0.572 8～0.752 2(60 cm)，均达到极显著水平。相关系数有所减小；30 cm处的土壤含水率的相关系数整体高于60 cm处的相关系数，且随着二者距离的增大，相关系数的变化没有明显规律。因而进行墒情监测点布置时，点与点之间的距离在现有基础上应该有所增加。

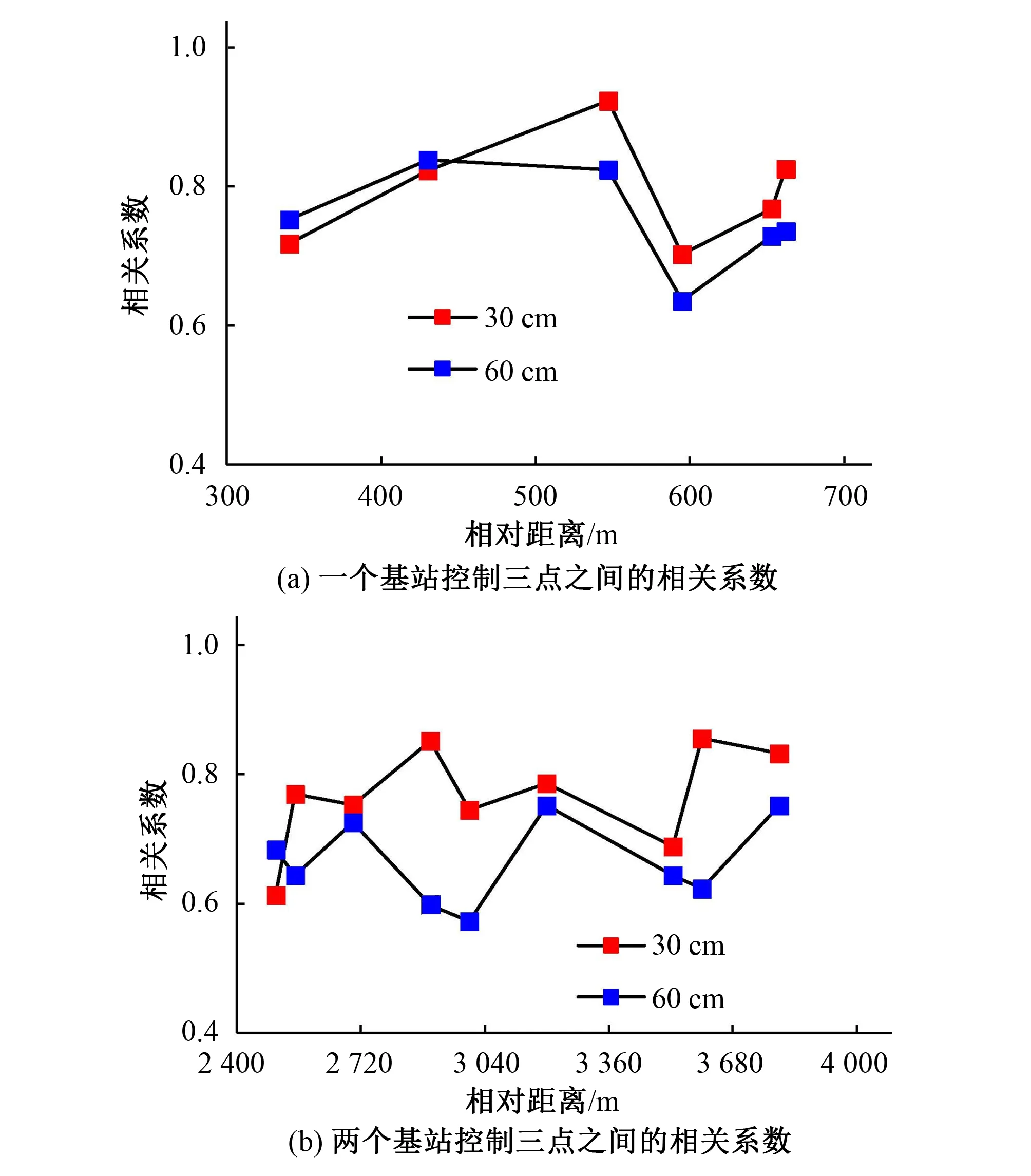
图4 各测点分层土壤含水率的相关系数Fig.4 Correlation coefficient of soil moisture content in each layer

2.3.2 3个测点土壤含水率相关关系分析

将6个测点按照式(6)进行组合，可得到60个组合，选取其中具有代表性的12种组合进行相关系数分析，可得到表3。

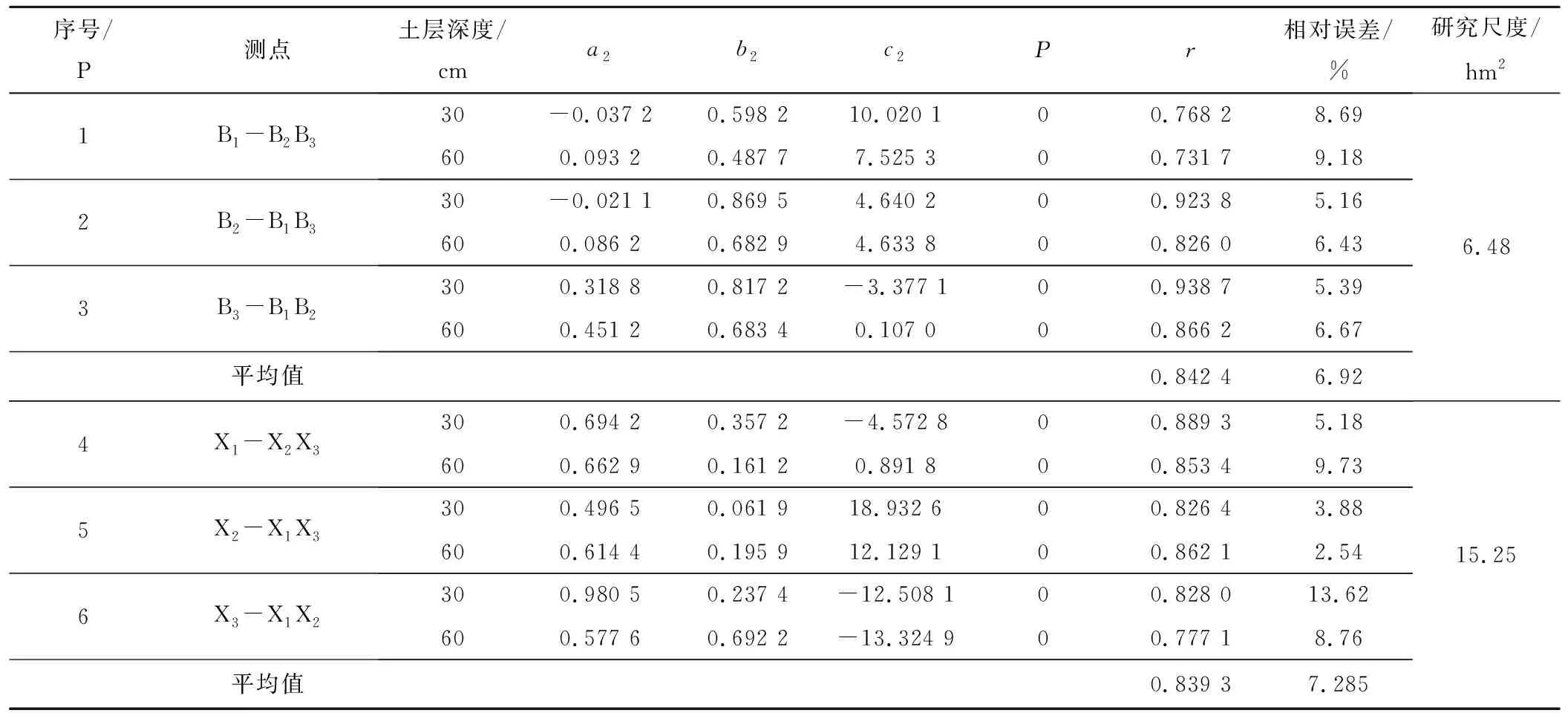
表3 3个测点土壤含水率相关关系Tab.3 Correlation among soil moisture content of three measuring points

续表3 3个测点土壤含水率相关关系

从表3可以看出，在测试期间，两个基站控制的6个测点的分层土壤含水率的相关系数变化幅度较大，变化于0.640 4～0.939 7，均值为0.787 8，相对误差变化于2.54%～13.62%，均值为6.82%；3个测点土壤含水率具有明显的线性关系，且参数a、b的值均小于1，常数c则无明显变化规律；表明6个测点的土壤含水率具有一定的关系，由此说明本研究中测点之间的相对距离可适当增大。

从表3还可以看出，随着试区尺度的增大(6.48、15.25、286.67 hm2)，土壤含水率的相关系数减小，研究尺度对应的相关系数平均值分别为0.715 5、0.705 8、0.547 2，主要原因是随着试区尺度的增大，影响土壤含水率变化的因素不断增多。该结果与马春芽和胡伟等研究结果一致，他们认为研究尺度在一定范围内增大，土壤含水率的变异系数逐渐增大[10,11]。也有学者认为土壤含水率的统计特征值(R2)随着研究尺度的减小而减小[9]，主要原因是该学者研究尺度较小(0.25、0.01、0.000 4 hm2)，远小于本研究的尺度。