掌纹主线和纹理特征融合的识别方法

文/张志敏

（长春理工大学计算机科学技术学院 吉林省长春市 130022）

随着信息技术的迅速发展和人类社会的不断进步，掌纹识别技术[1]-[5]成为一种新兴的生物特征识别技术，是近年来研究的热点之一。掌纹的主要信息集中在一个有效区域内，即感兴趣区域(RegionOfInterest，ROI)[6]-[8]。该区域不仅包含基于线的特征，还包含脊和细节点，这些特征是人与生俱来且长期不变的。与其他生物特征识别方法相比，掌纹图像易采集；用户接受度高；对图像的分辨率要求可降低；相对稳定的特征也可在低分辨率的图像中被提取。虽然传统的掌纹特征提取方法也可以较好地提取掌纹特征信息，但只能提取单一特征，导致提取的掌纹特征信息不够丰富。因此，特征融合成为掌纹识别领域的发展方向。掌纹识别技术中主要包含两种特征融合：

（1）掌纹与其他生物模态进行特征融合；

（2）采用不同方法提取掌纹的不同特征进行融合。

近年来，许多掌纹特征融合方法[9]-[11]相继出现。如文献[9]提出了一种利用多尺度LBP 算子和Gabor 滤波器相结合的方法对预处理后的掌纹ROI 区域进行特征提取。该算法首先利用关键点定位的方法对给定的掌纹图像做预处理操作，得到掌纹ROI 区域，然后采用双向直方图均衡化增强掌纹ROI 区域的对比度以及纹理细节，之后通过纹理频谱度量的方法对掌纹主线方向进行搜寻，确定Gabor 滤波器的方向参数，最后利用多尺度LBP 算子对Gabor 变换后的掌纹特征进行提取。实验结果表明，用该方法提取的特征进行掌纹的分类识别可取得良好的识别率，但该方法主要针对掌纹的纹理特征进行融合，并没有注重掌纹的其他特征。文献[10]提出了一种手形、掌纹和掌静脉多特征融合的识别方法。其中，提到了融合掌纹和掌静脉这两种特征的方法。该方法利用小波分解分别获得掌纹和掌静脉ROI 图像的高、低频分量，从中选取了掌纹和掌静脉的低频分量以及掌纹的水平边缘分量和垂直边缘分量。利用Gabor 滤波器对选取的分量进行了纹理增强，再采用融合规则对纹理增强后的掌纹和掌静脉低频分量进行融合，得到融合图像。将融合图像和Gabor 纹理增强的掌纹高频子图像经小波逆变换得到最终的掌纹和掌静脉融合图像，利用分块纹理基元模型对融合图像进行特征提取并进行识别率的验证。实验结果表明，当分块数目为3×3 时，其识别率高达98.36%，该方法虽然将人体手掌的手形、掌纹和掌静脉进行融合，但并没有将掌纹的多种特征进行融合。文献[11]提出了一种基于子空间与纹理特征融合的掌纹识别方法。该方法利用稳健线性判别分析算法提取掌纹ROI 区域的子空间特征，从而使特征维数得到了有效地降低。再将掌纹ROI 均匀分割成8×8 大小的非重叠子块，采用局部方向二值模式对每个子块分别提取主方向和相应的方向置信度以获取两者的编码值，进而得到其直方图。之后将每一个子块的方向二值模式直方图和置信二值模式直方图串联起来，从而获得局部方向二值模式的直方图特征，然后将获取的两种掌纹特征通过加权串联的方法实现特征融合，经验证，该方法取得了非常理想的识别率。虽然该方法识别结果非常理想，但在掌纹纹理特征的提取过程中计算量相对较大。

考虑到上述方法所面临的问题，本文重点针对掌纹ROI 的多种特征进行融合，同时从避免在掌纹纹理特征提取过程中计算量偏大的角度出发，提出了一种基于掌纹主线和纹理特征融合的掌纹识别方法。该方法首先利用数学形态学[12]-[13]对增强后的掌纹ROI 图像进行主线特征提取，然后再利用基于统一模式的LBP 算子[4]对其纹理特征进行提取，从而使整个纹理特征提取过程更为简捷实用，最后利用融合规则将提取到的两种掌纹ROI 特征进行融合，从而丰富掌纹ROI 的有效特征信息。对掌纹ROI 的各特征图进行直方图数据统计，将统计到的直方图数据作为特征向量输入到SVM 多分类器进行分类识别，得到识别结果。将识别结果与单一的主线和纹理特征的识别结果作对比，从而对多特征融合的掌纹方法的有效性进行验证。

1 掌纹主线和纹理特征相融合的掌纹特征提取算法

1.1 数学形态学

数学形态学是一种数学工具，由Matheron、Serra 等提出,先后经历了二值形态学和灰度形态学的发展过程。运用数学形态学可在一定程度上简化图像数据，使图像的基本形状特性得以保持,并把不相干的结构剔除。因此，这种方法在研究中的各个领域均得到应用，同样，它也可以实现掌纹主线的提取。

形态学图像处理的基本思想是利用预先定义的结构元素（也可以将结构元素当作滤波窗口）对信号进行匹配，达到提取信号，保持细节和抑制噪声的目的。最基本的形态学运算是膨胀，腐蚀，闭运算和开运算。

设f 为待处理的灰度掌纹图像，b 为结构元素。则膨胀运算定义为：

对图像做膨胀处理，一方面目标物体中的空洞能得到很好的填充，另一方面目标物体区域得到增大。另外，在一定程度上，它还具备去除噪声和平滑目标物体边缘的功能。

腐蚀运算定义为：

图1：掌纹ROI 的处理效果图

图2：掌纹主线的形态学后置处理

对图像做腐蚀处理，一方面可以剔除目标物体的孤立边缘点获得平滑边缘的效果，另一方面目标物体区域将会减小。另外，它在一定程度上可将噪声去除。

式（1-1）和式（1-2）中的Db 表示结构元素b 的区域范围，f表示待处理的掌纹图像。由这两个公式可以构造出形态学中另外两个重要的操作：开运算和闭运算。

闭运算定义为：

对图像进行闭运算，不仅可以将目标物体中的空洞很好的填充，而且还可以把目标物体的边缘进行平滑操作。另外，它还能去除噪声。

开运算定义为：

对图像进行开运算，目标物体的细小边界点得到了有效地去除，同时能够比较理想地分离目标物体。另外，它能把目标物体的边缘进行较好的平滑。

在开闭运算的基础上定义了Bothat 算子，也称低帽变换，是图像闭操作与原图像之差，因为它具有检测信号波谷的能力又称为波谷检测器。

由式（1-3）得到形态学Bothat 变换定义如下：

式中f 为输入图像，b 为结构元素。

将增强后的掌纹ROI 区域利用结构元素b 进行Bothat 运算，目的是把处在“波谷”的信息检测出来。同时为了将“波谷”信息与掌纹ROI 的黑色背景区域分开，本文利用大津发(OTSU)对Bothat 处理后的掌纹ROI 增强图像进行二值化，实验效果如图1(c)所示，结构元素b 的选取如式（1-6）所示。

从图1(c)可以看出：由于掌纹图像噪声和手掌乳突纹等客观存在，因此在一定程度上形成了干扰因素，从而导致一定量的伪特征点存在，这将严重限制识别准确率。因此为了提高识别准确率，就要对干扰点进行消除，这就需要对图1(c)的实验结果继续采用数学形态学的方法进行后置处理，处理步骤如下：

（1）消除干扰点：采用形态学开运算实现干扰点的消除，其中结构元素的选取是问题的关键，原因在于结构元素选大了，固然容易去除干扰点，但同时也容易删除纹线上不连续的细小纹线。而选小了，又达不到去除干扰点的目的，综合二者，本文选用了3×3的结构元素b1，如式（1-7）所示，效果见图1.2(a)。

（2）进一步消除细小干扰点：从图2(a)可以发现，经形态学开运算处理后的图像干扰点有了明显的减少，但还有一些细小的干扰点存在。为了删除这些细小的干扰点，首先统计图像经开运算处理后的白色连通区域，然后选择一个小区域，该区域明显小于主线的连通区域，但比细小干扰点的区域要大，利用这个小区域对开运算处理后的图像进行从上到下，自左向右的扫描，若当前连通区域小于本文选定的小区域，则被过滤掉，反之，则保留。经处理后的图像如图2(b)所示。

（3）连接断裂的掌纹纹线：从图2(b)可以看出，图像的干扰点基本上已经被去除了，但由于掌纹主线经过前几步形态学的处理，使一些原本连接的主线存在细小的断裂，因此需要一个形态学闭运算将断开的主线进行连接。鉴于掌纹纹线的走势，需要对结构元素进行合适的选取。考虑到通用的结构元素基本上不存在，结合自己提取的掌纹ROI 区域大都来自掌纹库的右手图像，其纹线走向如图1(a)所示。因此，本文选用结构元素b2 进行掌纹主线特征的提取，其效果如图2(c)所示，可以看到一些断开的纹线经闭运算操作后得到了有效的连接，结构元素b2 的选取如式（1-8）所示。

（4）加粗：从图2(c)可以看出，一些断开的纹线经闭运算操作后得到了有效的连接。由于闭运算是先膨胀后腐蚀，而腐蚀后的纹线会变得相对细一些，因此需要对其进行适当的加粗操作，得到的效果如图2(d)所示。此时，完成了掌纹主线特征的提取。

1.2 局部二值模式

局部二值模式[4][9][14]-[16]于1996年被芬兰奥卢大学的Ojala T 教授等人提出，该算子可以对纹理进行较好的描述。LBP 算子的显著优点是旋转不变性与灰度不变性，使用该算子得到的纹理信息更加稳定，计算量较少，能够捕获更多的细节信息，并能压缩冗余信息。

1.2.1 原始局部二值模式

原始的局部二值模式(LBP)会选用一个3×3 大小的窗口，该窗口中心位置的像素点就是阈值，将这个点周围的8 个点的灰度值分别与其进行比较，如果其周围像素点的值比中心点的像素值大，就把该像素点的位置标为1，反之则标为0。这样，一个点在3×3 邻域内的8 个像素点就产生了一个无符号数，之后根据其位置的不同赋予的权重也不同，通过求和会得到一个整数，也就是该点的LBP值，该值反映了选定区域的纹理信息。LBP 算子的计算公式如下：

其中，ic为窗口中心像素(xc, yc)的灰度值，为8 个相邻像素的灰度值，函数s(x)定义如下：

将增强后的掌纹ROI 图利用LBP 算子进行纹理特征提取，其效果如图3(b)所示。

由于原始的LBP 算子只覆盖了一个固定半径范围内的小区域，导致大尺寸结构纹理特征无法提取。因此，本文采用改进的局部二值模式(基于统一模式的LBP 算子)对增强后的掌纹ROI 进行纹理特征提取。

1.2.2 改进的局部二值模式

基于统一模式的LBP 算子是Ojala 对原始局部二值模式的改进，该模式有一个共同的特点，即最多只包含两次从1 到0 或从0 到1的跳变。因此，Ojala 定义了统一模式的LBP 算子：LBP 所对应的循环二进制数从1 到0 或从0 到1 最多有两次跳变，它的定义如式（1-11）所示。

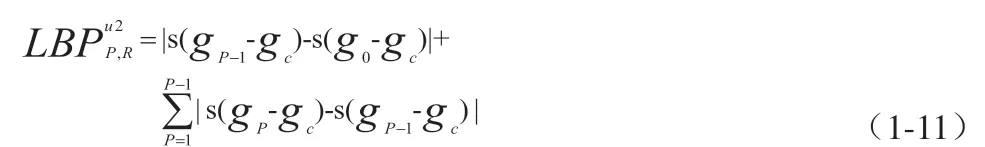
基于统一模式的LBP 算子对图像的暗亮点、边缘和平滑区域等都具有较好的描述能力，且该算子不仅可以表示纹理特征的基本信息，同时也能起到降维、减少二进制模式种类的作用。为了和原始LBP 算子形成对比，系统选用3×3 邻域即算子对增强后的掌纹ROI 区域图像进行纹理特征提取，处理效果如图4 所示。

1.2.3 多特征融合

由于数学形态学在提取掌纹主线特征的过程不涉及掌纹纹理特征，得到的特征图仅仅包含掌纹的三大主线，从而导致提取的掌纹特征过于单一。而基于统一模式的LBP 算子主要针对增强后的掌纹ROI 的纹理特征进行提取，而不注重主线特征，导致提取的特征也较为单一。因此，本文利用多特征融合的思想将本文增强方法增强后的掌纹ROI 经数学形态学和基于统一模式的LBP 算子获得的掌纹主线特征和纹理特征进行融合。

由于利用数学形态学提取增强后的掌纹ROI 主线特征数据是逻辑型，而用基于统一模式的LBP 算子提取增强后的掌纹ROI 纹理特征数据是uint8 型，所以无法使用融合规则直接将两种特征图像进行融合。考虑到逻辑型数据的特点是非0 即1，因此本文首先将增强后的掌纹ROI 主线特征的数据值域线性映射到[0,1]闭区间上，然后再将该ROI的纹理特征的数据值域由0-255线性映射到[0,1]闭区间内，以便使用融合规则进行融合。现用y1(i,j)表示增强后的掌纹ROI 的主线特征经数据转换后的主线特征数据，y2(i,j)表示增强后的掌纹ROI 的纹理特征经数据转换后的纹理特征数据，y3(i,j)则表示利用融合规则实现该ROI 主线特征数据和纹理特征数据相融合的多特征数据，融合规则如式（1-12）所示。由式（1-12）可知，其融合过程是对掌纹ROI 的主线和纹理特征数据的每一个数据按照由左至右，从上到下的顺序进行比较，将数值大的作为融合图像的数据值。之所以将数值大的作为融合图像的数据值，是因为增强后的掌纹ROI 主线特征经数学形态学等一系列操作处理后，提取到的主线特征数据经数据转换后会以数值1 的形式存储于计算机中，背景区域则以数值0 的形式存储在计算机内，而纹理特征数据经数据转换后被线性映射到[0,1]闭区间内。因此选取值大的一方作为融合图像的数据值，是为了将增强后的掌纹ROI 的纹理特征覆盖在相应的主线特征图的背景区域上，而主线特征的数值1 所在区域要比纹理特征的数据值大，所以主线特征会被很好的体现出来。各增强方法的主线、纹理特征融合后的效果如图5 所示。

表1：掌纹主线、纹理和多特征融合的识别结果对比

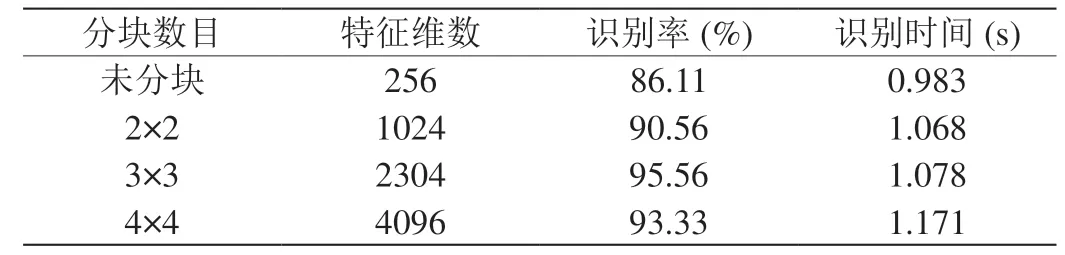
表2：掌纹多特征图分块识别比较

表3：本文方法与基于子空间与纹理特征融合方法的比较

图3：原始LBP 算子效果图

图4：原始LBP 算子效果图

图5：多特征融合后的图像

本文分别对主线、纹理以及多特征融合后的特征图的直方图数据进行统计，进而得到各特征图的特征向量并保存，为后续的分类识别阶段做准备。

2 分类识别

由于掌纹识别是一个多分类问题，因此需要采用SVM[17]-[21]实现掌纹的多分类识别。本文构建的SVM 多分类网络是通过使用多个SVM 二分类器实现掌纹的多分类，如果有n 类样本，则需要构造n(n-1)/2 个SVM 子分类器。对于需要进行验证的样本，一次性调用n(n-1)/2 个子分类器，然后每一个子分类器都会对其投票，最后统计票数，如果某一类的票数是最多的，则将该验证样本划分到那一类。

利用SVM 进行分类识别的过程如下：

2.1 对数据做归一化处理

经特征提取后的样本数据集被分为训练集和测试集，再对训练集数据和测试集数据做归一化处理，目的是为了避免大数值区间的属性过分支配小数值区间的属性，同时也可避免计算过程中的数值复杂度。

2.2 RBF核函数的选取

经Vapnik 等人的研究表明，SVM 的性能与核函数的选择关系并不大[4]，但核函数的参数以及惩罚系数对SVM 的性能却有着重要的影响。目前最常用的核函数是RBF 核函数，即高斯核函数，该核函数的优点是可以实现线性核函数的所有功能，反之则不成立；RBF 核函数需要的训练参数比多项式核函数少，且分类器较为简单。因此本文选用高斯核作为SVM 的核函数。

2.3 最优惩罚系数C和核函数的参数g的选取

关于SVM 最优参数的选取，国际上并没有公认统一的最好的方法，因此本文将训练集作为原始数据集并利用交叉验证法进行最优参数寻找，即将训练集验证分类准确率最高的那组C 和g 作为最优参数。

2.4 训练分类模型

将选定的RBF 核函数和最优参数C、g 以及归一化处理后的训练集数据及其对应的编号输入到构建的SVM 网络进行训练。

2.5 进行验证样本的测试

训练集数据经第（4）步处理后会得到训练模型，依据训练模型将归一化处理后的测试集数据及其对应的编号输入到构建的SVM 网络进行分类，从而得到识别结果。

3 实验结果及分析

为了对本文算法有效性进行验证，我们从中科院掌纹库中挑选45 组，每组8 幅图片且均来自同一个人的同一只手，共360 个掌纹样本。将这些掌纹图片进行预处理、特征提取后，每组每张掌纹ROI 图片都对应着自己的特征向量。为了便于后续的多分类识别，需要对这些特征向量进行编号处理，从而进行类别划分，即第一组的8 张掌纹ROI 图片对应的特征向量统一编号为第1 类，第二组的8 张掌纹ROI 图片对应的特征向量统一编号为第2 类，依此类推，则掌纹样本的类别数目是45 个。之后从每类随机选取4 张掌纹ROI 图片对应的特征向量(共180 个特征向量)构造训练集并输入到SVM 进行训练，将剩下的每类四张掌纹ROI 图片对应的特征向量(也是180 个特征向量)作为测试集，输入到SVM 进行分类，同时输出识别率和所消耗的时间。

本文将掌纹ROI 主线特征图、纹理特征图和多特征融合后的特征图所对应的特征向量均采用SVM 分类器进行分类识别，得到识别结果。对单、多特征的识别结果进行对比，从而证明基于本文增强方法的多特征融合算法的有效性，实验结果如表1 所示。

从表1 可以看出：多特征融合后的识别结果高于主线和纹理特征的识别结果，且识别消耗时间较为理想，进而证明基于本文增强方法的多特征融合算法的有效性。为了进一步提升识别率，本文将多特征融合的图像进行分块处理，统计每块子图的直方图数据并将其排列后作为特征向量输入到SVM 分类器进行分类识别，实验结果如表2 所示。

从表2 可知：共有四组实验数据。从特征维数来看，第一组为基于本文增强方法的多特征融合图不经分割直接统计直方图数据，该组特征维数是256 维。第二组是进行2×2 的分割，共得到4 幅子图，然后统计每幅子图的直方图数据并将其进行排列，构成特征向量，该组维数是1024 维。第三组进行了3×3 的分割，其特征维数是2304 维。第四组则是4×4 的分割，虽然该组分割最为细致，但其特征维数高达4096 维。从识别率和识别时间来看，随着分块数目的增多，识别率并非递增，而是达到一个最高值后呈现下降的趋势，即当分块数目为3×3 时，识别率最高，且识别消耗时间相对理想。而当分块数目为4×4 时，不仅识别率会降低而且识别时间也有所增加。究其原因是因为过多的分块会导致信息冗余和特征维数增加，从而降低识别率和延长识别时间。

为了对本文识别结果的有效性进行验证，本文与文献[11]的方法作对比。该文献提出的基于子空间与纹理特征融合的方法是一种多特征融合算法，和本文方法在一定程度上是非常相似的。利用稳健线性判别分析和局部方向二值模式分别获取掌纹图像的子空间特征和纹理特征；基于加权串联方法实现子空间特征与纹理特征的有效融合。

本文将文献[11]所提方法和本文方法均在同一个掌纹样本数据集上分别进行预处理、特征提取等相关操作，得到特征向量。再使用SVM 分类器进行识别率的验证，并比较两种方法的识别结果，如表3 所示。

通过表3 可知，本文方法在识别率上比文献[11]提出的方法高出了1.12%。究其原因是因为本文在预处理环节对掌纹ROI 区域的特征信息进行了有效的增强，从而在特征提取阶段可获得更为丰富的掌纹ROI 特征信息因此可获得更高的识别率，这进一步表明本文方法的改进效果是有效的。

4 结论

本文提出了一种基于掌纹主线和纹理特征融合的掌纹识别方法。该方法重点针对掌纹ROI 的多种特征进行融合，同时从避免在掌纹纹理特征提取过程中计算量偏大的角度出发，利用数学形态学对增强后的掌纹ROI 图像进行主线特征提取，然后再利用基于统一模式的LBP 算子对其纹理特征进行提取，从而使整个纹理特征提取过程更为简捷实用，最后利用融合规则将提取到的两种掌纹ROI 特征进行融合，从而丰富掌纹ROI 的有效特征信息。对各特征图进行直方图数据统计，将统计到的直方图数据作为特征向量输入到SVM 多分类器进行分类识别，实验结果表明多特征融合的掌纹ROI 图像取得的识别率更高。再将识别率最高的特征图进行分块处理并与其他方法作对比，实验结果表明当分块数目为3×3 时识别率最高，且高于基于子空间与纹理特征融合的识别率。