基于熵值修正BWM的煤炭企业绿色供应商选择 评价模型及应用

曹一哲，杨玉中

(河南理工大学 能源科学与工程学院，河南 焦作 454000)

伴随着全球环境保护意识的增强以及各个国家相关环境法规的日益完善，现代制造企业面临的环境要求更加严格，同时，市场对于高绿色度产品的需求也日渐增长。因此在这样的外部环境下，环境因素逐步成为企业采购环节中最重要的考虑因素。对于核心企业而言，选择合适的绿色供应商，不仅可以解决企业对于高绿色度原材料的依赖，也可以缓解企业后续生产过程中的环境问题。此外，通过与绿色供应商建立合作关系，也有利于企业实施绿色供应链管理，提高企业的可持续发展能力。绿色供应商选择与评价是典型的多属性决策问题，在绿色供应商选择与评价过程中，需要决策人根据绿色供应商评价指标体系对众多备选绿色供应商进行评价，然后根据评价的结果从中选优。因此，评价指标体系中指标权重系数确定的准确性和有效性，直接决定着绿色供应商选择与评价的结果。

对于绿色供应商评价指标赋权问题，常用的方法一般可分为主观赋权法、客观赋权法以及主客观组合赋权法。其中，主观赋权法以AHP法[1-4]、ANP法[5-6]等方法为代表，指标权重的确定完全依靠决策人或专家的知识经验。客观赋权法以熵权法[7]、DEA[8]等为代表，指标赋权是根据指标原始数据之间的变异程度来确定的，具有较强的数理依据。在赋权结果上，主观赋权法体现了完全决策人对评价指标的偏好程度，但是结果带有一定的主观性和随意性；客观赋权法过于依赖指标数据，赋权结果不稳定，不能体现决策人或专家对评价指标的重视程度。主客观组合赋权法则是利用几种不同的主客观权重通过方法组合的方式进行赋权，该赋权方法在一定程度上弥补了单独使用主客观赋权法对评价指标赋权的缺点。现盛行的组合赋权方法有加法合成法、乘法合成法、基于客观修正主观组合方式和极差最大化组合方式。在2017年，李刚等学者针对现有的主客观组合赋权方法，即现在盛行的组合赋权方法，分析了这四种组合方式的合理性，结果显示，基于客观修正主观和极差最大化组合方法是合理的[9]。

本文通过客观修正主观的权重组合方法，应用熵值法和BWM(最优最劣法Best-worst method)法，构建基于熵值修正BWM的组合赋权方法，对绿色供应商评价指标体系进行赋权。在此基础上，结合TOPSIS法提出绿色供应商选择模型，并通过煤机制造企业的零件供应商选择问题验证该模型的可行性。

一、煤炭企业绿色供应商评价指标体系

通过对以往以绿色供应商选择与评价方法、绿色供应商评价指标体系、绿色供应商绩效评价以及相应的英文关键词分析，在以其为主题的书籍著作、期刊论文和学位论文等相关的资料中查阅发现，在绿色供应商评价指标中，体系指标的选取主要集中在产品质量、采购成本(产品价格)、供应商服务(交货期限)、供应商企业能力(竞争力)和绿色指标5个方面上。因此，借鉴过往的研究成果并结合对煤炭企业的走访，从供应商产品质量和经济效益、企业竞争力和环境保护3个方面出发，构建如表1所示的煤炭企业绿色供应商评价指标体系，在该体系中以质量、成本、供应商能力、绿色发展能力和服务水平及信誉5个指标为一级指标。在一级指标中，质量和成本确保了供应商产品的质量和经济效益、供应商能力和服务水平及信誉保证了供应商企业自身的竞争力，绿色发展能力体现了供应商在企业环境保护方面的成效。本文结合已有的研究成果及一些制造企业技术和管理人员的意见，确定了煤炭企业绿色供应商评价指标体系，如表1所示。

其中，价格稳定性C21是指供应商提供的产品在一年内价格上下波动超过5%的次数；技术水平C32是指可用工程技术人员与该企业中职工总数的比值，即技术水平=(可用技术人员/企业职工总数)×100%。定性指标的数据是采购企业对供应商企业进行实地考察后进行综合打分的分数。

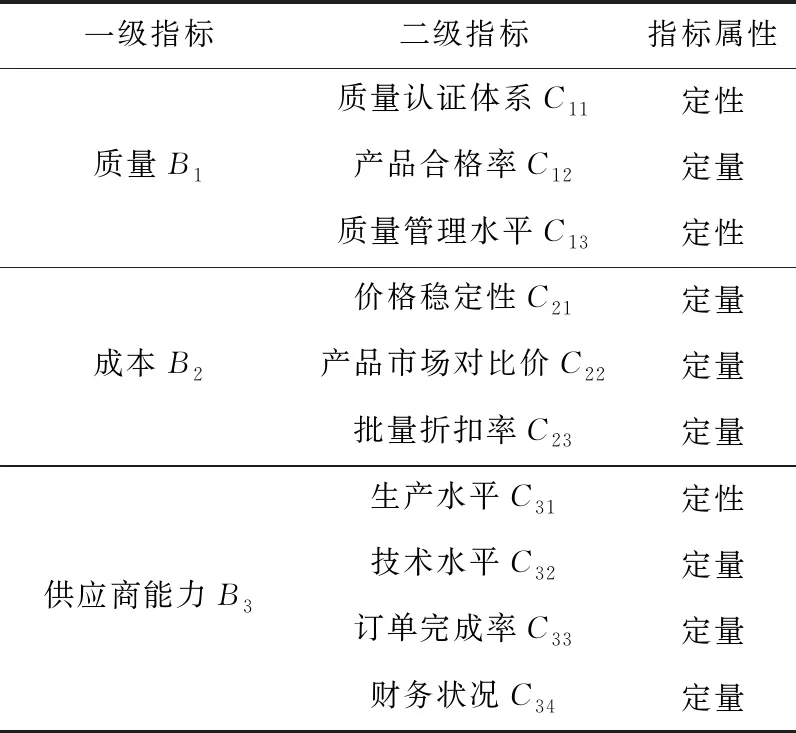
表1 煤炭企业绿色供应商评价指标体系

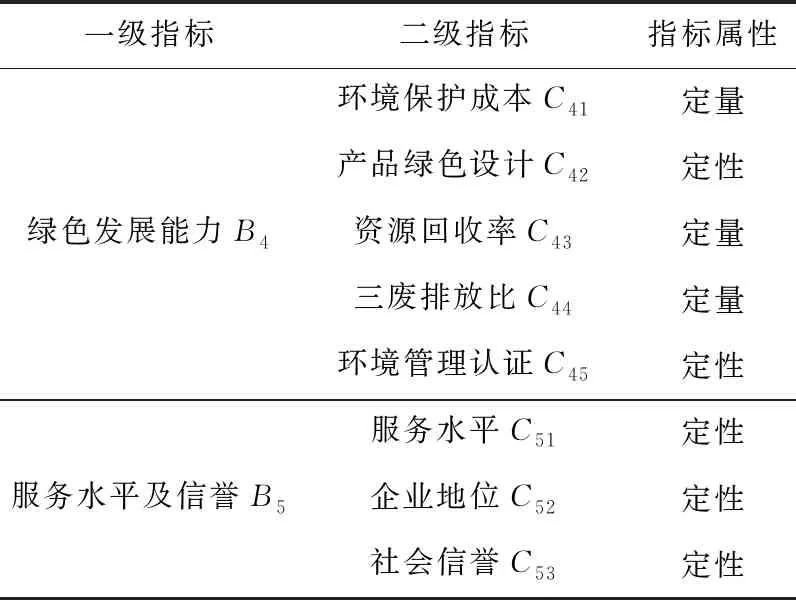
续表1 煤炭企业绿色供应商评价指标体系

二、基于熵值修正BWM的TOPSIS绿色供应商选择评价模型

2015年，最优最劣方法(BWM)由荷兰学者Rezaei提出的一种新的多准则决策方法[10]。该方法是基于评价准则之间两两成对比较的思想，通过决策者从评价指标体系中选取最优指标和最劣指标，再与其他指标进行两两比较，构造了最优指标比较向量和最差指标比较向量，与传统的两两比较方法相比，BWM方法只需要进行2n-3次比较。对于通过指标成对比较的方式确定指标权重的赋权方法而言，其面临的最大的挑战是成对比较矩阵一致性的缺失[10]。而BWM通过选取最优和最劣指标再进行两两比较的方式，大大简化了比较过程，进而降低了不一致风险，使得权重计算结果更为可靠。

(一)基于熵值修正BWM法的评价指标赋权方法

考虑到BWM法在赋权过程中，对于最优指标和最劣指标的选取，以及指标的打分都是依靠决策人的主观判断而得到的，因此为了避免该方法的主观性，本文通过利用熵值可以表达供应商原始数据离散程度的特性，根据指标熵值的大小对指标的重要性进行排序。根据重要性排序结果，选择最优指标和最劣指标，构造最优比较向量和最差比较向量，从而得到评价体系中各个指标的权重。

1.计算各指标的熵值

在信息论中，熵可以表示对不确定性的一种度量。信息量越大，不确定性就越小，熵也就越小；信息量越小，不确定性越大，熵也越大。在评价指标中，熵值是用来反映被评价指标的变异程度，通过计算信息熵值来判断某个指标的离散程度。熵值越小，该指标的离散程度越大，表明该指标对综合评价的影响越大，其权重应该越大；反之，表明指标数据分布集中，其信息量小，所分配的权重也应该越小。

设有m个绿色供应商，矩阵R为第i个供应商始属性值矩阵

其中，rij为第j个指标下第i个供应商的原始属性值。

(1)

(2)

根据式(1)和式(2)计算出各指标的熵值ej。

其中，k=1/Inm；由于构建的煤炭企业绿色供应商评价指标体系为二层评价指标体系，因此，取二级指标熵值的平均数作为其上一级指标的熵值。

2.指标重要性排序

根据评价指标熵值的大小进行重要性排序，其中指标的熵值越小，表示该指标的离散程度越高，其重要性越高。如果某两个指标的熵值大小一样则表示这两个指标的重要性相同。

3.BWM法确定各级的评价指标权重

步骤1：通过熵值的大小对各个准则内的指标进行重要性排序。然后选取重要性最大的指标作为最优指标cB，重要性最小的指标为cW。

步骤2：利用选取的最优指标与其他指标进行两两对比，并用1～9的数字表示最优指标相对于其他指标的偏好程度，构造基于最优准则的比较向量AB=(aB1,aB2,…,aBn)。其中，aBj表示最优指标(相较于其他指标的偏好程度)。

步骤3：利用其他指标与选取的最差指标CW进行两两比较，与上一步骤类似，构造基于最差准则的比较向量Aw=(a1W,a2W,…,anW)T。

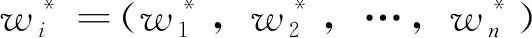
Minξ

s.t.

wj≥0,j=1,2,3,…,m

(3)

表2 CI取值

若CR<0.1表示通过一致性检验；CR≥0.1表示未通过一致性检验。尽管，BWM法同样是运用CI和CR指标对指标打分的一致性进行检验，但当指标比较向量不满足一致性时，只需要对最优指标比较向量和最劣指标比较向量中的取值进行相应调整即可，相较于其他成对比较的方法而言，指标打分修正的工作也比较便捷。

(二)TOPSIS法对备选绿色供应商排序与选择

1981年，TOPSIS是由Hwang和Yoon提出的方法，它借助多属性决策问题的正理想解和负理想解对评价对象进行排序。该方法基本思想是采用欧式距离，通过确定有限方案点与正负理想解之间的距离，然后计算各方案与正理想解的贴近度，并根据贴近度的大小对方案进行排序，即靠近理想解又远离负理想解的方案就是最佳方案。TOPSIS法与其他评价方法相比，计算相对简单，结果量化客观以及与其他决策方法结合灵活等特点，在多准则决策问题研究领域应用广泛。

TOPSIS法对备选绿色供应商进行评价排序的过程为：

步骤1：将原始矩阵R进行无量纲化处理，得到规范化矩阵Z为

(4)

步骤2：将规范化矩阵加权得加权规范化矩阵V为

(5)

步骤3：确定正理想解v*和负理想解v0为

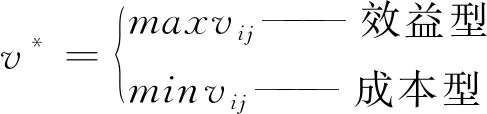
(6)

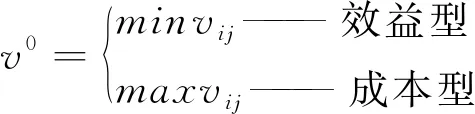
(7)

步骤4：备选供应商与正理想解和负理想解的距离分别为

(8)

(9)

步骤5：计算各备选供应商的相对贴近度Ci。各供应商根据其Ci值的大小进行排序，其中Ci值越接近于1的为最优供应商

(10)

三、应用分析

某煤矿机械装备制造企业由于受煤炭行业影响，业务数量及营业额大幅度降低。为了企业的生存与发展，该企业开始开拓新业务——立体车库的研发与制造。由于原有供应商无法提供新业务需求的一些特殊的零部件，因此该企业需要一个新的绿色供应商为其提供新业务需求的零部件。现有5家绿色供应商通过了初选，分别记为A、B、C、D和E。根据已构建的煤炭企业绿色供应商评价指标体系，对5家供应商进行数据收集，其中定性指标需要专家以10分制打分法获得，定量指标则参考企业原始数据，然后根据式(1)对原始数据进行处理得到矩阵P，结果如下所示。

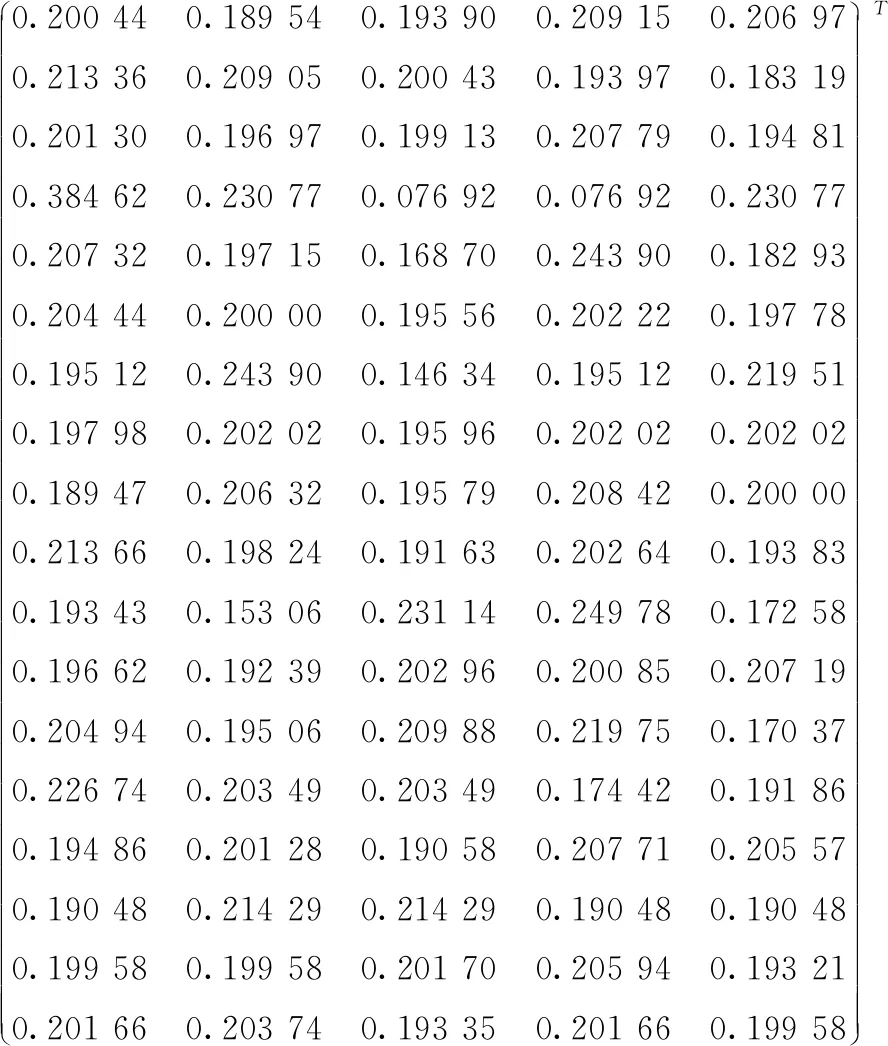
(一)基于熵值修正BWM确定指标权重

基于熵值修正BWM确定指标权重包括二级指标熵值、一级指标熵值、BWM法确定各级指标的权重，他们计算结果以及重要性排序分析如下。

(1)计算二级指标熵值及重要性排序。根据式(2)求得二级指标的熵值并根据其熵值大小进行重要性排序，结果如表3所示。

表3 二级指标熵值及重要性排序

(2)计算一级指标熵值及重要性排序。一级指标熵值由其二级指标熵值的平均数求得，然后根据其熵值的大小进行重要性排序，结果由表4所示。

表4 一级指标熵值及重要性排序

(3)BWM法确定各级指标的权重。以一级指标为例，运用BWM法确定一级指标的权重。

根据重要性排序选取成本B2为最优指标，质量B1为最差指标。利用指标B2与其他指标两两比较得最优比较向量为：A2=(9,1,2,2,3)。利用其他指标与B1指标之间两两比较的最差比较向量为：A1=(1,9,6,6,4)T。

根据式(3)构建如下数学规划

Minξ

s.t.

w1+w2+w3+w4+w5=1

wj≥0,j=1,2,3,4,5

运用matlab求得结果由表5所示。

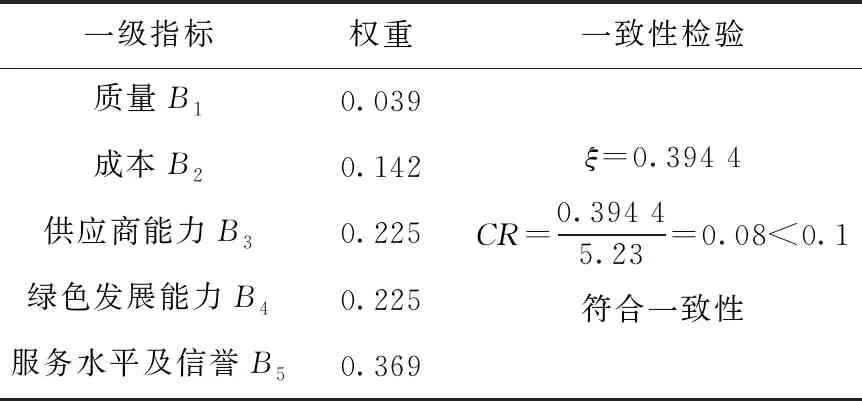
表5 一级指标权重及一致性检验

同理，可以确定二级指标的权重,其结果如表6所示。

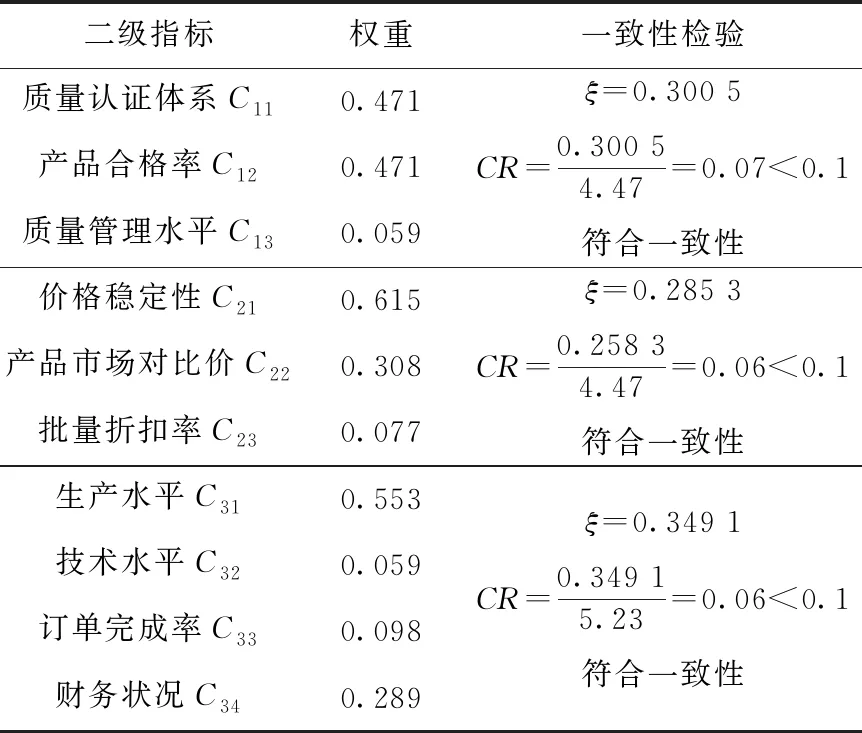
表6 二级指标权重及一致性检验

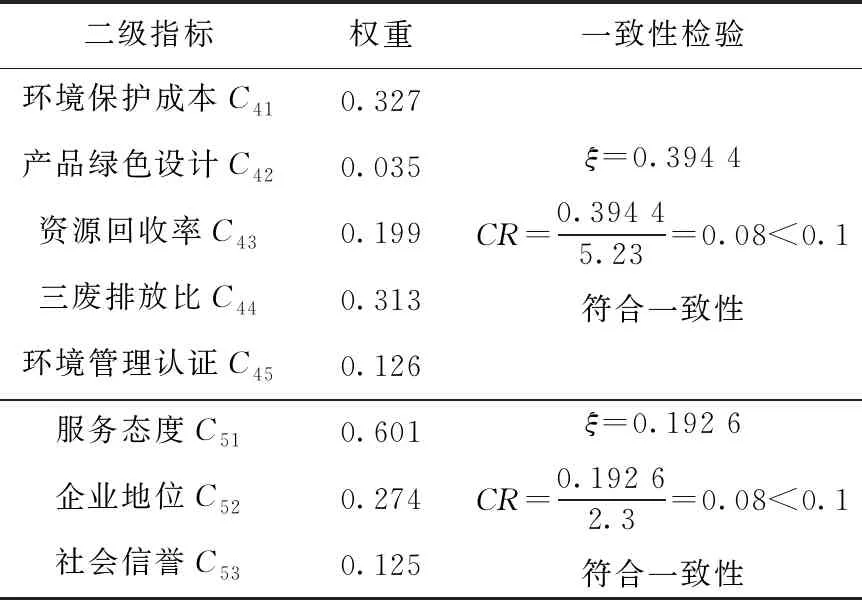
续表6 二级指标权重及一致性检验

由于评价指标体系为多层结构。因此二级指标对于目标的综合权重如表7所示。

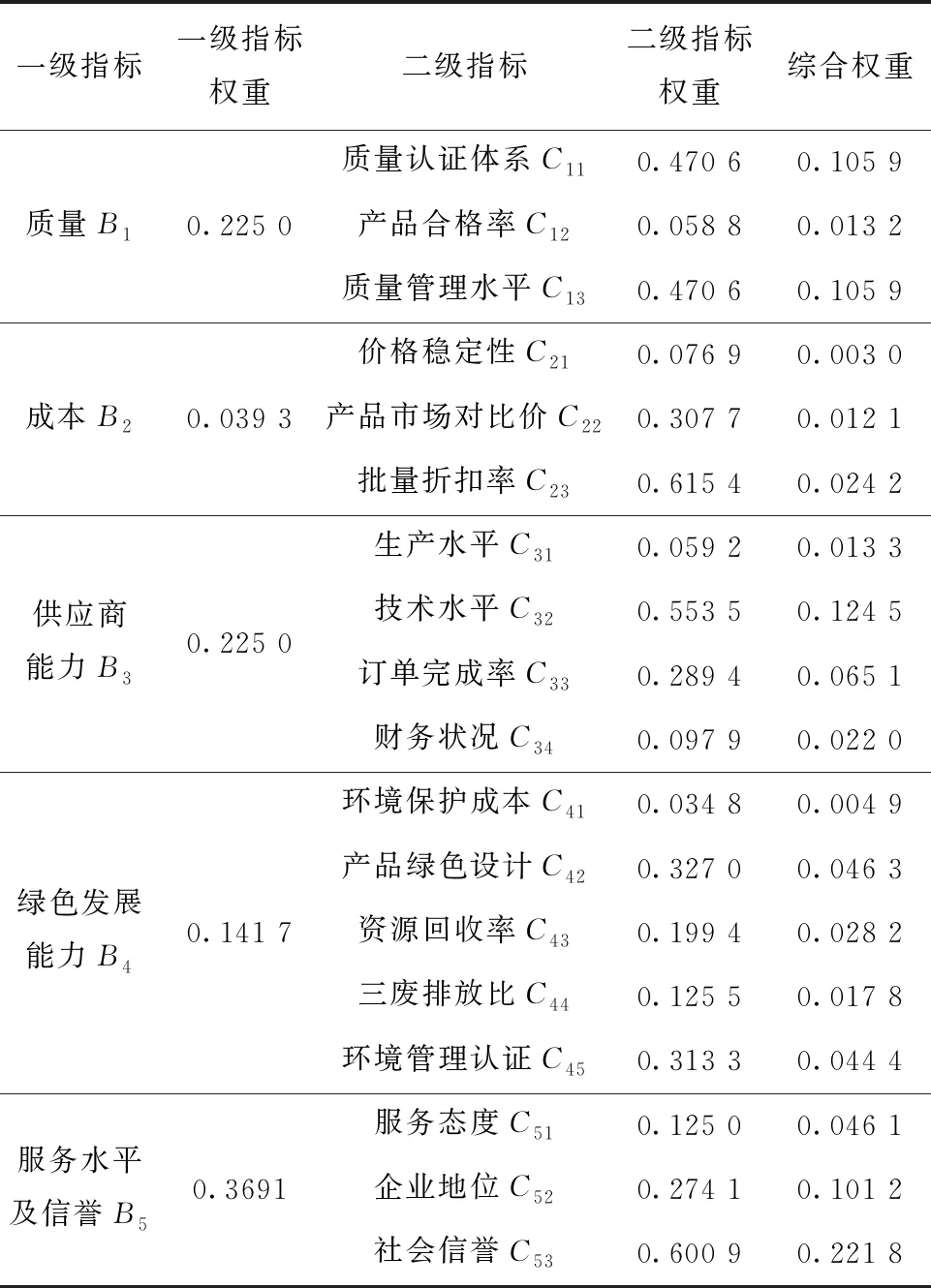
表7 综合权重

(二)TOPSIS法备选供应商评价选优

根据式(4)将原始数据矩阵R进行无量纲化处理，得到规范化矩阵Z，结果如下所示。

根据式(5)将BWM法求得的综合权重对规范化矩阵Z进行加权处理得到加权矩阵V，结果如下所示。

根据式(6)和式(7)计算出正理想解和负理想解，再根据式(8)、式(9)和式(10)计算出5家备选绿色供应商与正负理想解的距离以及相对贴进度，结果如表8所示。

表8 各绿色供应商与正负理想解距离及相对贴进度

由表8可以看出，供应商C和供应商D相对贴进度最接近1，其次是供应商B和供应商E。因此，可以选择供应商D为最佳绿色供应商，而供应商C可以作为备用供应商选项。

四、结 论

绿色供应商选择是绿色供应链管理的关键环节之一，针对绿色供应商选择问题，首先构建了包含质量、成本、供应商能力、绿色发展能力和服务水平及信誉5个一级指标，质量认证体系、产品合格率、质量管理水平等18个二级指标的煤炭企业绿色供应商评价指标体系，其次采用基于熵值修正BWM的组合赋权模型对指标进行赋权，并结合TOPSIS法对煤炭企业绿色供应商进行优劣排序，选择最优供应商，最后在某煤炭机械加工企业中对所建立的评价指标体系和选择模型进行应用，为其选择最优绿色供应商。采用BWM法作为煤炭企业绿色供应商评价指标体系的赋权方法，可以简化比较过程，减少指标之间的比较次数，在一定程度上也降低了打分不一致的风险。利用熵值反映数据离散程度，采用客观修正主观的组合赋权方式，通过计算熵值大小构造指标的重要性排序代替BWM法在选取最优指标和最劣指标中完全依靠决策人经验的主观判断，确保最优指标和最劣指标选取更具有说服力和合理性，也使得赋权结果更加科学。