燃气联合循环机组供热期最佳真空探讨

张 添 李学宾

（1、北京京能清洁能源电力股份有限公司，北京100028 2、北京京西燃气热电有限公司，北京100041）

凝汽器的最佳真空是指在一定的机组负荷（电负荷和热负荷不变）工况下，改变冷却水条件，机组功率增量收益与冷端设备耗功增量支出之差值最大时的真空值。汽轮机运行的经济性与最佳真空相关，汽轮机厂家一般只提供阻塞真空曲线，而不提供最佳真空曲线，当然这与机组整体设计也有关系。但是，机组的最佳真空与机组的经济性息息相关，对机组的经济效益影响很大，是电厂最关注指标之一。因此得出机组的最佳真空数据对于各个电厂都有很迫切的需要，能够取得很大的经济效益。

1 试验方案的确定

典型的燃气联合循环机组为二拖一布置方式，即两台燃机轮机拖一台汽轮机运行。两台燃气轮机通过燃烧天然气做功，排汽进入各自余热锅炉，两台余热锅炉产生的蒸汽再一起进入汽轮机做功。由于燃气轮机组发电成本高，基本都在大城市，冷却方式不能采取传统的冷却塔，一般采用机力塔风机冷却，普遍存在冷却能力不足，在非供热工况，凝汽器真空远大于5KPa，已经大大偏离了最佳真空范围，没有研究价值，因此本文主要探讨供热期机组的最佳真空。

严格意义上，若想需找最佳真空，试验时应该解除机组负荷AGC（自动发电控制）及CCS（协调控制），手动选定燃机负荷后，再进行冷端设备调整试验。这样在固定燃机负荷情况下，消耗天然气量将不变，这时启动一台风机后计算汽机负荷的增量收益△Pt 是否大于机力塔风机消耗的支出△Pp。当△Pt 与△Pp 差值最大时，这时的真空为机组的最佳真空；当△Pt=△Pp，这时的真空值为机组的最大经济性真空。

由于机组运行中不具备解除AGC 和CCS 条件，只能在稳定工况直接进行机力塔风机启停试验。试验在AGC 指令不会发生变化的时段进行，一般选择在前后夜负荷稳定的工况进行。试验过程中，机组总负荷按照AGC 指令维持不变，维持供热量不变。若试验前机组功率为P1+P2+P3=P0，则启动一台机力塔风机后，三台机负荷将变为P12+P22+P32=P0，其中两台燃机负荷下降，汽机负荷上升，且汽机的负荷增量等于两台燃机的减少量以维持总负荷不变，即（P1- P12）+（P2- P22）=△P32，（△P32=P32- P3）。由于AGC 的调节，启动机力塔风机后两台燃机负荷下降，因此汽机负荷的上升实际是小于理想试验方案中汽机负荷的上升的。因此只要△P32 的收益＞机力塔风机多消耗厂用电支出即为合算的，且结果更保守。

机组的最佳真空是随着机组的负荷变化而变化的，通过试验的方法只能对不同的机组负荷分别试验，才能得出不同工况下的最佳真空。这里通过在不同负荷下，通过试验得出几组不同工况下的最佳真空数据，根据这些数据就能拟合出机组负荷与最佳真空曲线。

按照试验方案，选择了几个稳定试验机组工况进行了最佳真空的试验，为了避免试验数据误差，采取5S 一个点的取样周期，然后选取每次变工况前10 分钟共120 个点取平均得出数据，尽量避免数据误差。

2 最佳真空计算方法

通过求解以凝汽器压力、冷却水温度和冷却水流量为变量的目标函数得出凝汽器最佳运行背压。在一定的机组负荷和冷却水流量条件下，汽机功率增量减少的天然气成本与机力塔风机多耗厂用电增加支出之差值为最大时的凝汽器压力即为最佳运行真空。

根据这一原则建立的目标函数为：

Pt：汽机负荷；

tw：循环水温度；

Ga：抽真空设备不同运行方式下的抽空气量；

Gw：循环水流量；

△Pt：汽机负荷增加减少成本；

△Pp：机力塔风机增加的支出。

由于Ga 和Gw一定，则可以得出当公式（2）成立时对应的真空为机组该工况下最佳真空，即：

要求解方程（2），则需要得出△Pt、△Pp 与tw 函数，即汽机负荷增加的收益与循环水温度关系曲线y1、机力塔耗电增加支出与循环水温度关系曲线y2 这两条曲线。另外为了求解最佳真空，还需要循环水温度与真空曲线y3。

通过实际试验数据绘制出这三条曲线，并模拟出趋势线方程式，将y1、y2 两个方程代入公式（2），即可求出该工况下最佳真空对应的循环水温度，在将计算的循环水温度代入y3，即可反算出该工况下对应的最佳真空值。

3 试验工况及数据计算

供热期间，进行了多次稳定负荷工况下的启停机力塔风机试验，根据实际数据，这里我们进行了六次试验，将试验结果计算汇总如下：

3.1 机组负荷612MW、供热量1350GJ、凝结水流量205T 工况最佳真空计算。

下表1 为根据2015 年3 月4 日试验数据提出得出的数据表：

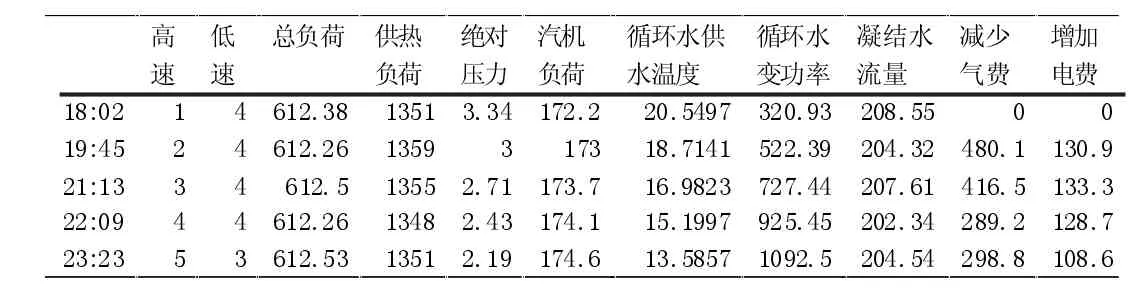
表1 612MW、1350GJ、205T 工况数据表

根据表1 数据可以汽机负荷增加的收益与循环水温度关系曲线y1、机力塔耗电增加支出与循环水温度关系曲线y2、循环水温度与真空曲线y3 三个方程，分别如下：

若y1=y2,可以求出x1=13.57℃，代入y3 可以得出对应真空为2.19KPa；

将y1、y2 代入方程（2），可以求出x2=15.6℃，代入y3 可以得出对应真空为2.49KPa。

3.2 数据汇总

同以上方法，计算了其他五次试验数据，得出下表2 最佳真空试验数据汇总表如下：

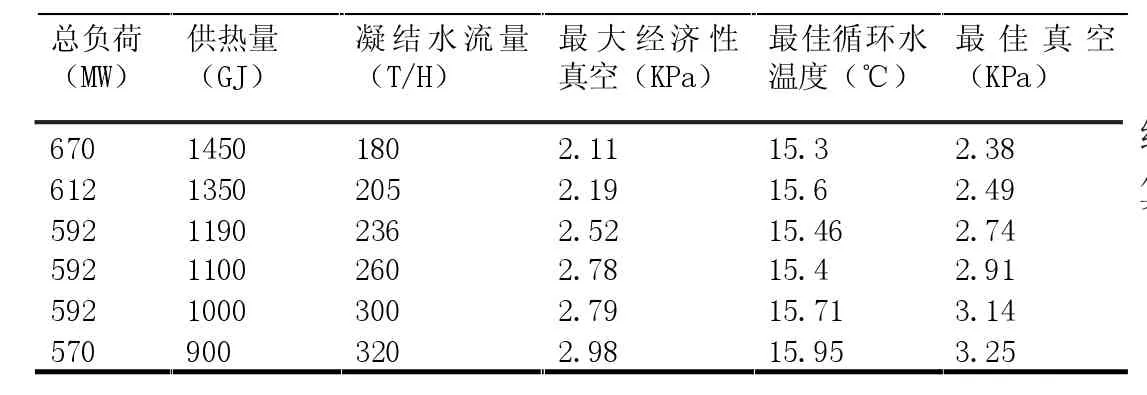
表2 最佳真空试验数据汇总表

4 最佳真空曲线

供热期，该机组稳定供热量基本维持在1000-1400GJ，此次试验工况覆盖了运行时所有供热工况。在供热期，凝汽器的负荷实际上为低压缸排汽，排汽量越大，凝汽器负荷就越大，也就是凝结水母管出口流量，因此根据表2 数据，可以得出最大经济性真空曲线和最佳真空曲线如下图1。

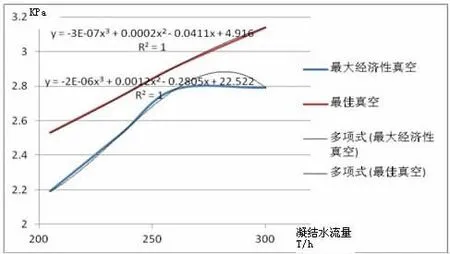
图1 最佳真空曲线图

则可以得出凝结水流量与最大经济性真空曲线公式如下：

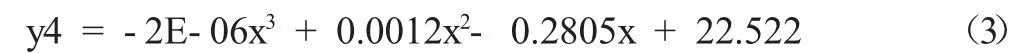
凝结水流量与最佳真空曲线公式如下：

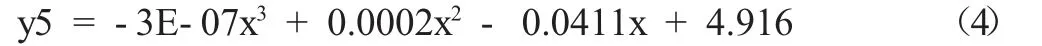
5 结论

根据以上可以得出，随着机组负荷和供热量的变化，机组的最佳真空是一个变化量，这里我们以凝结水流量最为变量，得出了凝结水流量与最佳真空的关系，基本覆盖了稳定运行时的数据，在凝结水流量180-320T/H 时，最佳真空数值在2.38-3.25KPa 之间线性变化。

因此，在机组的实际运行过程中，要根据机组的供热量的变化，按照凝结水流量的数值，合理的选择运行真空，尽量保持在最佳真空状态运行已保证机组获得最大收益。

6 经济效益计算

根据试验结果，将机组运行真空控制标准值由之前的3.5KPa±0.5KPa 修改为2.6KPa±0.3KPa。实际机组平均运行真空由以前的3.6KPa 降低至2.6KPa，机组平均运行真空下降1KPa。

这里采用一组实际试验数据进行经济效益估算，下表3 为2015 年2 月22 日一组实际试验数据：

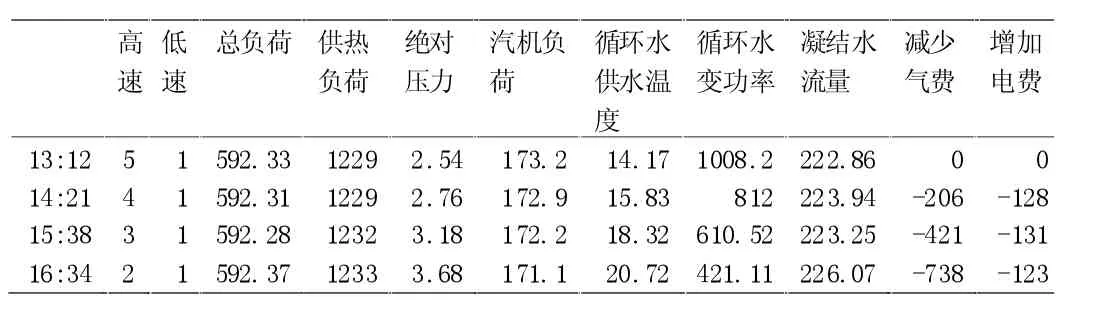
表3 2 月22 日592MW、1230GJ、224T 工况数据表

从上表3 可以看出，机组真空从2.54 上升至3.68KPa 时机组收益减少984 元/H，折合23616 元/天。按照供热季122 天计算，整个供热季节约成本288 万元。