基于灰色关联度的BP神经网络模型短期用电量预测
2020-06-10邓雪凝
邓雪凝
(华北电力大学 北京市 102206)
电网运行规划的经济性和科学性是电力系统安全、稳定运行的基础,负荷预测是电力系统调度、发展规划的前提。短期的社会用电量预测与很多社会因素有关,制定合理的电源建设规划,有利于提高电力系统的经济效益和社会效益。因此建立合理的社会用电量预测模型尤为重要。预测短期社会用电量的方法有很多种,最常用的方法有时间序列法、趋势外推法、线性回归法等。时间序列法过于突出时间因素在预测过程中的作用,而忽略了社会其他因素的影响,存在着预测误差的缺陷。新兴的方法有支持向量机和人工神经网络等。全社会用电量由各用电领域电能消耗量构成,不同的行业用电规律各不相同,与用电量关联度高的因素预测较为准确。本文将不同的社会用电量影响因素进行灰色关联度分析预测关联度、进行排序,将关联度高者作为全社会用电量主要影响因素指标。再建立BP神经元网络模型对安徽省全社会用电量进行预测,提高预测的精度和可靠性。
1 用电量预测方法
1.1 灰色关联度的原理及步骤
1.1.1 灰色关联度的原理
关联度即对于系统中某些因素随时间或其他因素变化的关联度大小的量度。在系统发展过程中,两个或多个因素发展趋势相似的程度各有高低,即为关联度的高低。灰色关联度分析便是衡量因素之间发展趋势的相似或相异程度的方法。灰色系统的概念相对于黑色系统,即全部信息已知的系统,和白色系统,即全部信息未知的系统,通过对信息的不确定性分析中找出因素本身及因素之间的数学关系,提取建模所需变量。
1.1.2 灰色关联度分析步骤
Step1 确定参考数列(分析标准)及比较数列(分析对象)

Step2 数据归一化处理
由于不同的数据量纲各不相同,故进行量纲统一化即数据归一化,减少数据之间差异,统一到相似区域,从而重点关注不同种类数据之间的变化趋势。此处我们使用数据初值化,将每一种数据都除以该种数据的第一个,同种数据间的量级不会有太大差别,并且可以将所有数据都收敛在1的范围内。

图1:BP神经网络示意图

图2:BP神经网络算法步骤

Step3 确定各数据所对应的权重λ
一般确定权重需要利用层次分析法等,为简便,此处我们直接将所有数据权重统一,因有m个比较序列,则权重皆为。
Step4 计算关联系数ζ:


表1:2000-2015逐年数据

表2:2016-2018年预测值及误差统计表
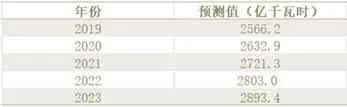
表3:未来五年预测值
可得到关联系数矩阵:

其中,
Step5 计算灰色加权关联度:

Step6 评价分析
将灰色加权关联度进行排序可得出不同比较序列的关联度高低,便可提取出建模所需变量。
1.2 BP神经网络模型原理与步骤
1.2.1 BP神经网络原理
1986年,以Rumelhart和McCelland为首的科学家小组提出了神经网络模型,根据人脑神经元工作原理模拟运行,在数据预测、图像处理等领域得到广泛的运用。
BP神经网络的拓扑结构是由三层及三层以上的多层神经网络组成的,其分为三个部分:输入层、隐含层、输出层。每一层由许多个神经元构成,且每一左右层之间都有连接权重,上下层之间没有连接。神经网络按照有导师学习方式进行训练,一组输入数据进入输入层,通过与隐含层的权重产生新的一组输入数据作为隐含层的输入,通过每一层不同的激活函数进行下一层的输入,以此类推,最终到达输出层并得到输出值。
由于每一层之间的连接权重会因输入输出发生变化,从而到达输出层时,会与真实结果产生误差,因此需要进行误差反馈,从输出层到每层隐含层进行连接权重的修正,使误差达到最小,从而得到最接近真实结果的输出值。BP神经网络示意图如图1所示。
1.2.2 BP神经网络算法步骤
第一步:确定样本数据
在(-1,1)区域内确定输入层与隐含层连接权重pij,输出层与隐含层连接权重qjk,隐含层阈值δj,输出层的阈值ωk。
第二步:选取输入训练样本及期望输出
第三步:计算各层神经元输入及输出
(1)利用输入样本数据Xp, 输入层与隐含层连接权重pij,隐含层阈值δj计算隐含层神经元输入:


(3)利用隐含层神经元输出βj,输出层与隐含层连接权重qjk,输出层的阈值ωk计算输出层神经元输入Tk:

(4)利用传递函数h(·)及输出层神经元输入Tk,计算输出层实际输出:

第四步:调整各类参数
(1)利用输出层与隐含层连接权重qjk,输出层误差δk,隐含层各神经元输出βj计算隐含层各神经元误差λ(p)j:


(3)利用隐含层各神经元误差λ(p)j,输入样本数据Xp计算调整输入层与隐含层连接权重pij和隐含层阈值δj,设 为一[0,1]的实数,为训练系数1:
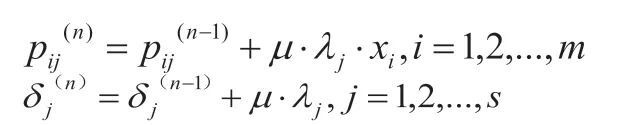
(4)利用输出层误差δ(p)k,隐含层各神经元输出βj计算调整输出层与隐含层连接权重qjk和输出层的阈值ωk,设η为一[0,1]的实数,为训练系数2:

第五步:计算全局误差E,当误差足够小达到精度要求便可以完成学习,否则再返回第四步继续迭代计算调整,进行下一轮训练。
2 实例预测
本文以表1所示的安徽省2000-2015年逐年全社会用电量(亿千瓦时)、第二产业增加值(亿元)、第三产业增加值(亿元)、安徽省人口(万人)、安徽省GDP(亿元)数据为基础,按照本文提出的基于灰色关联度的BP神经网络预测模型对安徽省全社会用电量进行未来5年的预测。
算法具体步骤如下:
(1)按照2.1.2部分中灰色关联度模型步骤计算第二产业增加值、第三产业增加值、省人口、GDP四项影响因素指标与安徽省全社会用电量的关联度,计算结果分别为:10.1265、11.6322、9.9688、10.774。由于安徽省人口与全社会用电量的关联度在四者中最低,因此不将安徽省人口作为社会用电量的主要影响因素。
(2)按照2.2.2部分中BP神经网络模型步骤进行预测,将第二产业增加值、第三产业增加值、GDP作为训练样本,设置网络参数及网络迭代次数N为3000次,期望全局误差ε为0.02,预测2016-2018年全社会用电量数据,并与实际数据进行比较,计算误差率。具体算法步骤如图2所示。
算法完成后,对2016-2018全社会用电量的预测数据、实际数据,并统计出误差率如表2所示。
3 实际预测
从表2可看出预测值得误差率基本维持在0.0123左右,满足全社会用电量的基本预测需求。因此可以用于预测未来五年的全社会用电量。预测结果如表3所示。
4 结语
本文首先采用灰色关联度模型选取安徽省第二产业增加值、第三产业增加值、GDP作为全社会用电量主要影响因素,再结合BP神经网络模型进行安徽省短期用电量仿真预测,在用电量预测过程中,控制误差率在0.0123左右,证明了本文数学模型的准确性和实用性,并预测了未来五年的安徽省全社会用电量,为电网运行规划提供了良好的技术支撑。
