贝叶斯网络分类模型在银行客户信用评估中的应用

夏春梅

（滨州学院信息工程学院 山东省滨州市 256603）

1 引言

分类是数据挖掘中的核心问题，基于统计理论的朴素贝叶斯算法能够预测所属类别的概率。由于简单朴素贝叶斯分类器假设一个指定类别中各属性的取值是相互独立，因此，它能够有效减少在构造分类器时所需要的计算量。目前，对朴素贝叶斯算法的研究以及基于该算法的应用非常成熟。

贝叶斯网络分类器是性能良好的分类器，贝叶斯网络分类模型有较好的可解释性，具有其它数据挖掘工具所不具备的优点，因其能够提供关于事物的本质的认识，可以对扰动的目标做出预测，非常适合应用在解决商业信用评估问题中，是作为建立分类模型的理想选择。[1][2]贝叶斯网络及其分类器不像朴素贝叶斯算法的应用那么成熟，它还正处于研究和发展之中，有大量的问题有待于研究解决。

数据挖掘涵盖极其广泛的应用领域，在不同的领域解决不同的问题需要有针对性的研究，需要对问题所在的领域有较好的理解。本文从朴素贝叶斯分类算法和贝叶斯网络分类器出发，根据具体商业应用银行客户信用评估的数据挖掘要求对现有的算法进行应用，并实现分类的目的。首先介绍相应的算法模型，其次，将银行客户信用评估的实际问题与贝叶斯分类模型结合在一起，使用Weka平台中已有的算法模型来解决实际问题。

2 在Weka平台进行数据分析

2.1 数据的预处理

使用NaiveBayes算法和TAN算法对CustomerEvaluation数据集建立分类模型。由于NaiveBayes算法可以处理数值型的属性，在使用NaiveBayes算法时，不用把每个变量都离散化成分类型。但是TAN算法不能处理数值型的属性，只能处理所有属性都是分类型的情况，所以在使用TAN算法进行数据处理时需要将数值型的属性离散化成分类型。

在银行客户信用评估数据集CustomerEvaluation中一共有18个属性，其中有6个属性变量是数值型的，这些属性的离散化需要借助Weka中的名为“Discretize”的Filter来完成。在区域中点击“Choose”，出现一棵“Filter树”，逐级找到“Weka.filters.unsupervised.attribute.Discretise”，单击，“Choose”旁边的文本框显示“Discretize-B10-M-0.1-R first-last，单击文本框，即可弹出新窗口，在新窗口中即可修改离散化的参数。

2.2 使用NaiveBayes算法处理数据

首 先，使 用“Explorer”打 开 数 据“CustomerEvaluation.arff”。然后，切换到“Classify”选项卡，点击“Choose”按钮后即可看到很多分类或者回归的算法按照类别分类列在一个树型框里。[3]因此银行客户信用评估数据集的输入属性中有“Binary”型和数值型的属性，而Class变量是“Binary”的，因此需要勾选“Binary attributes”、“Numeric attributes”、“Nominal attributes”和“Binary class”选项，点“OK”按钮后回到树形图，发现不能使用的算法名称变成红色。之后，再选择“bayes”下的“NaiveBayes”，算法名称没有变红，表示其可以使用。最后再单击“Choose”右边的文本框，弹出新窗口为该算法设置各种参数，点“More”查看参数说明，点“Capabilities”查看算法适用范围，这里所有的参数都选择默认值。在“Test Option”中，因为没有设置专门的检验数据集，为了保证生成的模型的准确性而不至于出现过拟合问题，因此采用10折交叉验证来选择和评估模型。

2.3 使用TAN算法处理数据

可以按照类似NaiveBayes算法处理数据的操作步骤来使用“TAN”算法对数据集进行处理。用“Explorer”打开数据“CustomerEvaluation.arff”，然后切换到“Classify”选项卡，点击“Choose”按钮后即可看到很多分类或者回归的算法也是一样的按照类别分类列在一个树型框里。选择“TAN”算法，点击“Choose”右边的文本框，弹出新窗口为该算法设置各种参数，这里所有的参数也都选择默认值。在“Test Option”中，同样是因为没有设置专门的检验数据集，为保证生成的模型的准确性而不至于出现过拟合问题，因此同样采用10折交叉验证来选择和评估模型。

2.4 测试结果

因为采用10折交叉验证来选择和评估模型，因此，操作上首先选择“Cross-validation”，然后在“Folds”框里面填上“10”，之后，点“Start”按钮让算法生成决策树模型。在“Classifier output”中会出现用文本表示的一棵决策树，以及对这个决策树的误差分析等结果。下面是使用NaiveBayes和TAN算法得到的测试结果。

NaiveBayes的测试结果：

3 测试结果分析及风险决策

3.1 结果分析

测试结果表明“NaiveBayes”模型的准确度是76.04%，“TAN”模型的准确度是77.62%。当然，如果想要再提高算法模型的准确度，可以对原属性进行一些处理或者修改算法的参数等途径来实现。

NaiveBayes算法模型的结果说明，在银行客户信用评估中，在7000个有还款能力的贷款人被预测为有还款能力的有6081个，被预测为正确的概率为6081/7000=86.87%，但是在有还款能力的人中有919/7000=13.13%的概率被错误的预测为无还款能力；在无还款能力的3000人中，有1523/3000=50.77%的概率被错误的预测为有还款能力，有1477/3000=49.23%的概率被正确预测成无还款能力。(6081+1523)是被预测为有还款能力的实例个数，(6081+1523)/10000=0.7604是被预测正确的分类实例所占比例，因此Confusion Matrix矩阵中主对角线上的数字越大副对角线上数字越小，说明预测的准确度越高。

TAN算法模型的结果说明，在银行客户信用评估中，在7000个还款能力的贷款人被预测为有还款能力的有6192个，被预测为正确的概率为6192/7000=88.46%，但是在有还款能力的人中有808/7000=11.54%的概率被错误的预测为无还款能力；在无还款能力的3000人中，有1430/3000=47.67%的概率被错误的预测为有还款能力，有1570/3000=52.33%的概率被正确预测成了无还款能力。(6192+1570)/10000=0.7762是被预测正确的分类实例所占比例，同样，Confusion Matrix矩阵中主对角线上的数字越大副对角线上数字越小，说明预测的准确度越高。

3.2 风险决策

在分类决策中，使得分类出现错误的概率达到最小是最重要的。但是在银行客户信用评估中，风险是比出现错误的概率更重要更需要考虑的问题。[4]在银行客户信用评估中，对客户贷款的分类不仅要尽最大可能的做出正确的判断，更重要的是要考虑到如果做出了错误判断的时候会带来什么样的后果。在客户信用评估中如果把“信用优秀的客户”错误的预测为“信用极差的客户”，这样的后果是银行仅仅损失一笔利息收益。但是，如果把“信用极差的客户”错误的预测为“信用优秀的客户”，这样的后果是银行可能会损失本金和利息，显然是造成了更大的损失。[5]两种错误预测所造成的后果是有很大差别的，后者的造成的损失明显比前者更大。[6]

在Weka的Classify菜单下，选择分类器后，在Test Options选项卡中点击More options选中Output Predications可以以分类概率百分比的形式输出各个事例的概率分布，结果如下：

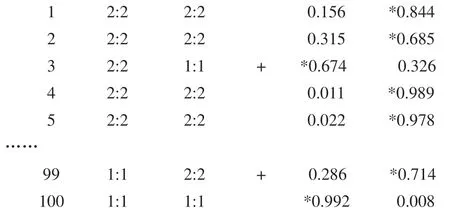
上面的列出的数据只是整个结果中的部分数据，事例是银行客户信用评估数据集CustomerEvaluation.arff中的真实数据。具体以事例3为例来说明在决策风险中的应用，事例3中预测为具有还款能力的客户的概率为0.674，大于50%，不具有还款能力的概率0.326，所以分类器把其计入信用优秀客户的类中。如果加入风险决策评估系数，假设信用优秀的客户被错误预测为信用极差客户的损失权重为2，信用极差客户被错误预测为信用优秀客户的损失权重为8，预测正确分类损失权重为0，当然在具体实践中可以根据实际情况更改权值系数值。有了权重系数以后，计算事例3记入优秀客户类的损失为0.674*0+0.326*8=2.608，事例3记入信用差客户类的损失为0.674*2+0.326*0=1.348，很显然，事例3被记入信用差客户类的损失比记入信用优秀客户类的损失要小的多。所以从风险决策的角度来说，根据最小风险规则，事例3记入信用差客户类更合适，而不应该计入信用优秀客户类中。

4 结语

本文在银行客户信用评估数据集上对选择的两种贝叶斯信用评估模型进行了10折交叉验证的实证研究，对两种评估模型得到的分类结果进行了对比。实验结果表明，使用贝叶斯网络分类器进行客户信用分类可以取得较高的准确度，但是在对信用极差客户的预测上没有朴素贝叶斯分类的好。贝叶斯网络分类器不仅具有较好的可解释性，也可以进行相关的改进后具备处理混合属性变量的能力，因此，从总体上来说，贝叶斯网络分类在信用评估上比朴素贝叶斯分类要好，是信用分类问题的理想选择，实验结果中较高的分类准确度说明贝叶斯网络分类器适合用于解决信用评估这类具有复杂非线性关系的分类问题。