强噪声下的微弱信号检测技术

李妙珍 李舜酩

（南京航空航天大学 能源与动力学院 江苏省南京市 210016）

在工程应用中，通常需要利用系统在工作过程中产生的微弱信号来对系统的工作状态进行判断。例如，旋转部件在工作过程中所产生的某些特定振动信号可以反映系统的工作状态以及系统的健康水平，但是此类有效信号通常会被较强的噪声所掩盖，使有效信息难以被提取，因此，研究微弱信号检测技术尤为重要。

微弱信号检测是利用近代电子学和信号处理方法从噪声中提取有用信号的一门技术学科[1, 2, 3]。它利用电子学、信息论和物理学的方法，研究噪声和有用信号，检测被噪声背景或干扰信号淹没的微弱信号。

1 线性检测方法

微弱信号的线性检测方法一般分为时域分析法和频域分析法和时频分析法。

1.1 时域分析法

时域分析方法更加适用于检测周期性的微弱信号，常用的方法包括相关检测、锁相放大、取样积分与数字式平均、时域平均等方法[4]。

相关检测通过对信号进行相关性分析，利用有用信号的相关性和噪声的随机性提取有用信号。相关性分为自相关函数和互相关函数两种。自相关函数用来描述同一信号在不同时刻取值的相关性[5]，设某一信号为x(t)，则其自相关函数为：

其值域为0-1。不同信号之间的相关性用互相关函数描述，设某组信号为x(t)和y(t)，则互相关函数为：

当Rxy(τ)=0时，x(t)和y(t)相互独立。

设待测信号为：

其中，s1(t)为有用信号，n(t)为噪声。用于互相关检测的参考信号为：

其中，s1(t)和s2(t)频率相同。则f1(t)和f2(t)的互相关函数为：

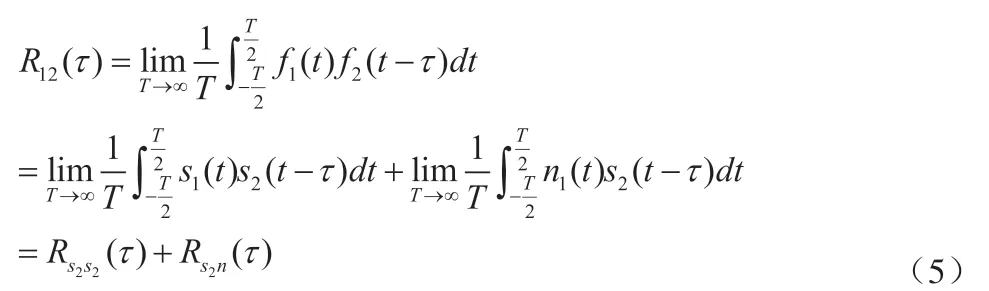
其中，Rs1s2(τ)为s1(t)与s2(t)的互相关函数，Rs2n(τ)为s2(t)与n(t)的互相关函数。因为噪声随机，与信号不相关，所以T→∞时有Rs2n(τ)=0，式（5）变为：

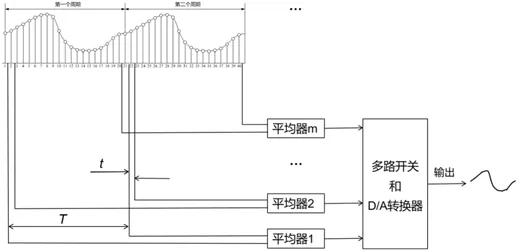
图1：取样和数字平均运算过程

此时得到的结果只与有用信号和参考信号有关，噪声的影响被去除掉了[6]。在进行相关计算时，由于信号长度有限，所以Rs2n(τ)≠0，这就是所谓的残留噪声[7]。

锁相放大技术利用的是互相关的原理，通过相敏检波器 (PSD) 和低通滤波器 (LPF) 完成互相关运算来检测微弱信号，克服了以往带通滤波器要求带宽窄而产生中心频率发生变化的问题[8, 9]。

取样积分与数字式平均技术是利用有用信号的周期性和噪声的随机性，在每个信号周期中取样多次，将每个周期中同一位置的信号相加，从而降低噪声对有用信号的影响，增大信噪比的一种微弱信号检测方法[10]。周期数越大，信噪比改善程度越大，但由于信号长度限制，噪声不能完全去除[11]。取样和数字平均运算过程如图1所示。

当用在非周期信号的检测工作中时，通常运用调制或者斩波的方法人为地给待测信号赋予周期[12]。焦光龙等人[13]利用平衡混频器能够消除本振噪声的原理，提高了取样积分器的稳定性。

时域平均是一种积累平均抗干扰过程，对输入信噪比没有要求，适合对淹没在强噪声里微弱信号进行预处理。此外，信号时域平均处理的结果是时域波形，易识别出信号的冲击特征，在故障诊断中被广泛应用。时域平均法对信号周期的要求较高，对此，陈韶华等提出了一种变截断周期时域平均搜索方法[14]，使其信噪比下限达到-35dB。

1.2 频域分析法

频谱分析法是频域分析的常用方法[15]。它利用傅里叶变换将信号转换到频域，提取出信号的频率成分、各谐波的幅值、相位、功率以及能量与频率的关系等信息。

频域分析法主要采用功率谱法进行微弱信号检测，主要用于检测平稳随机信号。功率谱估计是利用广义平稳随机过程的N个样本数据来估计该过程的功率谱密度[16, 17]。经典谱估计（非参数化方法）以傅里叶变换为基础，计算简便，但有泄漏效应，且方差性能不好；现代谱估计（参数化方法）以随机过程的参数模型为基础，具有频率分辨率高，能改善谱线分裂和频率偏移等问题的优点。

表1：各种检测方法适用范围和特点

在工程应用中，傅里叶变换在分辨率上有一定的局限性，另外用傅里叶变换的方法提取信号频谱时，需要利用信号的全部时域信息，所以缺少在时域上进行定位的功能[18]。频域分析方法主要用于平稳随机噪声下信号的检测[19, 20]。

1.3 时频分析法

当检测信号为非周期信号时，表述时间-频率局部性质成为必然要求。短时傅里叶变换和小波变换等时频分析采用时间 - 频率联合表示信号，可以全面反映观测信号的时频特征[21, 22]。

短时傅立叶变换是Gabor在传统的傅立叶变换的基础上提出的一种时频分析方法，可以看作信号在分析时间t附近由时间窗限定的一小段信号的“局部频谱”，代表时间t和频率f所确定的二维时频分布，这种算法的主要缺点是，一旦窗函数确定下来，时频分辨率就固定下来，因此缺乏细化功能。只有当基函数与信号尺度函数相匹配时，才能够检测出信号轮廓[23]。

小波变换的基本思想是将原始信号分解为一系列具有良好的时域、频域等局部特征的子带信号，进而实现对信号时间、频率的局部化分析。小波变换具有很强的去数据相关性，能够使信号的能量在小波域集中在一些大的小波系数中，而噪声的能量却分布于整个小波域内[24, 25, 26]。但小波基函数没有一个标准选择，对小波分解尺度范围的确定也没有一个通用的方法。

自1984年从事石油信号处理的工程师 Morlet 提出小波变换以来[27]，小波变换理论得到了迅速发展[28, 29]，并且被不断应用到故障诊断、解决残留噪声等问题中[30, 31, 32]。

2 非线性检测方法

为了便于分析，通常将非线性系统简化为线性系统，但精度较低，所以需要精度更高的非线性方法，主要包括混沌检测法、随机共振法、差分振子法[33]。

2.1 混沌振子法

混沌是非线性动力系统的固有特性。混沌理论最大的特点是混沌系统有不确定性，混沌系统具有对初值敏感性及对噪声免疫的特点[34]，因此，可通过观察系统相轨迹的变化实现微弱信号的检测。

基于混沌振子的信息检测技术主要有三种形式[35]：

（1）根据接收到的信号重构出混沌背景信号的相空间，得到混沌的预测模型，从待测信号中减去预测到的混沌信号，得到有用信号。

（2）利用混沌理论构造“混沌”测量系统，实现高精度的测量。

（3）使混沌动力学行为处于特定状态下，将待测信号作为混沌系统特定参数的补充，利用混沌系统对参数摄动的敏感性，根据混沌系统状态的相变实现对强噪声干扰下微弱信号的检测。

虽然混沌控制从总体上无统一的共同理论框架，但混沌控制都是利用连续小微扰变原来的正的Lyapunov指数为负值，实现从不稳定到稳定的转变[36, 37, 38]。

2.2 随机共振法

随机共振可以抽象概括为一种物理现象：利用噪声增强非线性系统中的微弱周期信号。

当非线性系统与输入的信号和噪声之间存在某种匹配时，如果增加输入噪声，输出信噪比反而大幅度增加[39]。利用随机共振理论设计非线性接收系统，可实现噪声能量向信号能量的转换[40]，在短数据集条件下检测更低信噪比的信号且不会产生误报现[41]。

随机共振的概念是由 Roberto Benzi、Alfonso sutera和Angelo vulpoiani等人于1981 年在研究古气象冰川问题时提出的[42]。在信号处理领域微弱信号检测方向，对随机共振已经有了大量的研究[43, 44, 45]。

2.3 差分振子法

与Duffing振子法一样，差分振子法也是利用非线性系统中参数的摄动引起周期解发生本质的变化来检测微弱信号[46]。差分振子法基于构造差分方程检测, 确定系统激励频率fe及检测频率fd，当被测信号中含有fd这一频率成分时，则系统产生共振，其相图随即发生变化，通过观察系统的相图变化来判断系统是否发生故障，实现早期故障的可视化检测[47，48，49]。且差分振子法只需求解一个差分方程组，计算量小[50]，适用于在线检测[51]。

3 总结

3.1 总结

本文分线性方法和非线性方法对微弱信号检测技术进行了介绍。其中，线性检测方法一般分为时域分析法和频域分析法和时频分析法。常用的时域分析法包括相关检测、取样积分与数字式平均等方法；频谱分析是常用的频域分析法；常用的时频分析法包括小波变换、短时傅里叶变换方法。混沌理论法、随机共振法和差分振子法是主要的微弱信号非线性检测方法。

在应用范围上，时域分析、频域分析适用于周期性信号的检测，而对于非周期信号而言，通常用时频分析法来对其进行检测。非线性系统可以在一些不稳定、非平衡的状态中提取信息，具有很强的灵活性[52]。

各个检测方法的适用范围和特点如表1所示。

3.2 展望

基于以上现有的线性、非线性检测方法，对微弱信号检测技术有以下的展望：

（1）目前对非线性方法的研究尚且不够，能够解决的非线性问题有限，所以对非线性检测方法还有待更加深入的研究。例如，寻找更加高效的自适应随机共振系统，使其可以自适应调整参数，更加高效智能地进行微弱信号检测。

（2）每种微弱信号检测方法都有其独特的优势，也有其难以克服和避免的缺点，如何更加高效完美地融合两种或多种检测方法，取长补短，以达到精度更高的目的，有待进一步进行研究和试验。例如，几种非线性方法之间既有不同点，又有相通点，可以以此角度研究它们之间的联系，将其有机结合起来，达到对更低信噪比信号的检测目的。