基于启发式割集法的桁架装配序列规划研究
2020-06-09姜冲张凯于淼
姜冲,张凯,于淼
基于启发式割集法的桁架装配序列规划研究
姜冲,张凯*,于淼
(四川大学 机械工程学院,四川 成都 610065)
目前关于桁架类产品的设计研究较少涉及其安装过程,传统的基于经验的安装模式很可能因为安装不得当,导致影响后续一系列同结构模块的安装质量,因此需要针对硬横跨的安装序列问题,优化安装流程,提高其安装效率和质量可靠性。本文研究了桁架类产品安装问题,提出了一种基于割集算法的启发式桁架装配序列规划方法。通过分析模型建立装配关联矩阵,简化装配关联矩阵减少安装序列搜索空间。使用基于启发式算法的割集发对简化之后装配关联图生成装配序列。最后使用单跨硬横跨模型为例生成安装序列,为硬横跨装配工艺设计提供了新的参考。
桁架;虚拟装配;装配序列规划;割集算法;启发式方法
装配是产品制造过程中最重要的一步,其在整个产品的制造过程中是最后一步,装配质量的好坏直接决定了产品最终的成型效果,早在1991年,Womack等人[1]就通过观察提出,装配耗时占据了产品制造总用时的20%~30%,而装配成本占总成本的40%。装配序列规划在装配流程中占有极其重要的地位,对装配质量起着决定性的作用。
对产品装配质量和产品装配周期的控制,都对设计人员提出了较大的考验,对其装配经验和设计成熟度有很高的要求,而且最后装配质量和时间成本往往因人而异,在装配设计上的标准性和规范性很难得到保障。装配序列规划(Assembly Sequence Planning,ASP)问题作为虚拟装配技术的关键一部分,设计人员可以在虚拟环境中进行编排规划,由计算机自动输出结果,能够极大程度缓解装配序列规划对人的依赖程度,完成装配的标准化规范化流程,减少因错误的装配规划导致的成本上升。
在ASP优化中,首要且最重要的步骤是建立并使用一种表达方法,以对装配问题进行建模。装配规划的有效性很大程度上取决于装配问题的建模方式。通常情况下,ASP问题表达形式分为三类:基于连接方式的建模、基于装配任务的建模以及基于零件的建模[2]。这些类别的划分都是根据其表示组装问题时的最小元素来定义的。其中超过半数的表达方式是基于零件建模,这很大程度上是因为研究人员试图模拟出组件中存在的最小装配体。
针对装配序列规划优化的研究主要有两个方向,一是传统上比较成熟的推理法,比如优先约束法[3]、割集法[4]等,二是基于元启发式方法的算法,比如遗传算法[5]、粒子群优化[6]、蚁群算法[7]、人工神经网络[8]等。上述规划优化算法都取得了良好的进展,但都是在全局进行序列搜索,在非可行解空间浪费了过多算力。
桁架结构作为一种在大型桥梁、机场穹顶以及输电线路中拥有广泛应用的结构,随着国内高铁建设的快速展开和布局,电气化铁路需要在站场中布置大量硬横跨来布设高铁动车所使用的接触网。特别是对于较大的枢纽场站,需要更复杂的硬横跨,因此对硬横跨的安装流程提出了更高的要求,一旦装配时出现不得当安装方式,将会出现严重的位移应力集中,影响硬横跨的长期使用。
本文提出了一种利用启发式算法与余树算法的改进式割集法来获得装配序列。减少了规划过程中所需同时考虑的零部件数量,提高了规划效率,避免了因同时计算的零件数量过多可能导致潜在的组合爆炸的情况。最后使用了单跨硬横跨模型验证了此方法。
1 系统设计
基于割集法的装配序列规划的生成流程主要如图1所示,首先需要将装配模型依据其连接关系,对零件分组编号使用无向图生成装配关联图,接下来聚类简化装配模型的表达,利用启发式规则分析层次关系确定层次关系建立割集,最后使用余树算法变换生成树,得到装配序列。
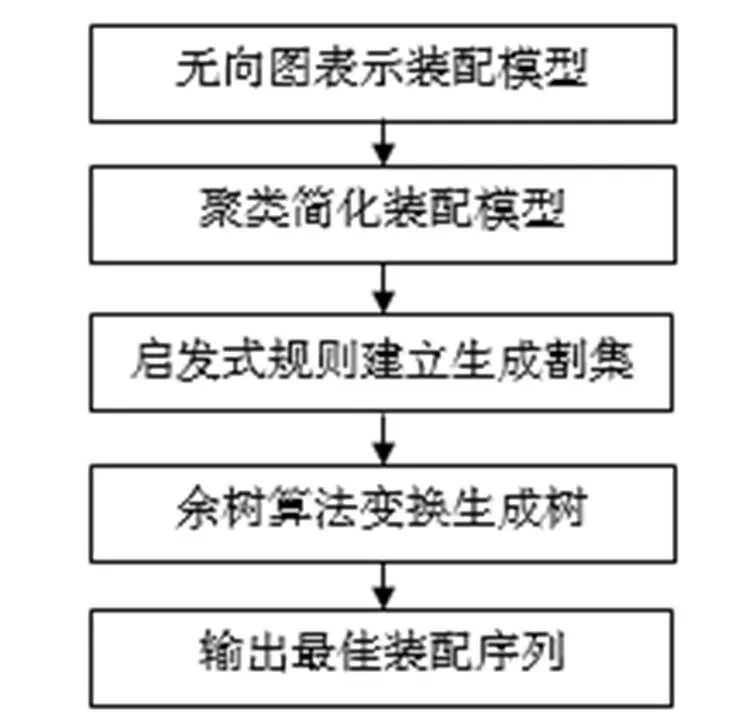
图1 装配序列规划的生成流程
1.1 装配模型表达
在此方法中,使用二维拓扑装配关联图来表示产品中零件的连接关系,表示形式为:

式中:为装配体中所有零件的集合;为零件之间的所有连接的集合。
为了得到装配关联图,还需要先将模型的零件进行标号。图2为某装配体的表示方式。已装配产品的拆解可以通过将关联图划分为子图的形式来表示,每一个子图都表示产品中的一个零件或者子装配体。分割图的弧的集合称为割集,用S表示。将某由五个零件组成的装配体拆分为两个子装配体,可以通过图2中表示为割集1={,,}来体现的。通过划分装配体并分析计算其基本割集,就可以得到其拆卸序列,如果将拆卸序列反向,就得到其装配序列。因为在装配过程中,同时需要安装三个或者更多零件的情况很罕见,所以使用基本割集将模型分割至单个零件以及仅含有两个零件构成的子装配体为止。
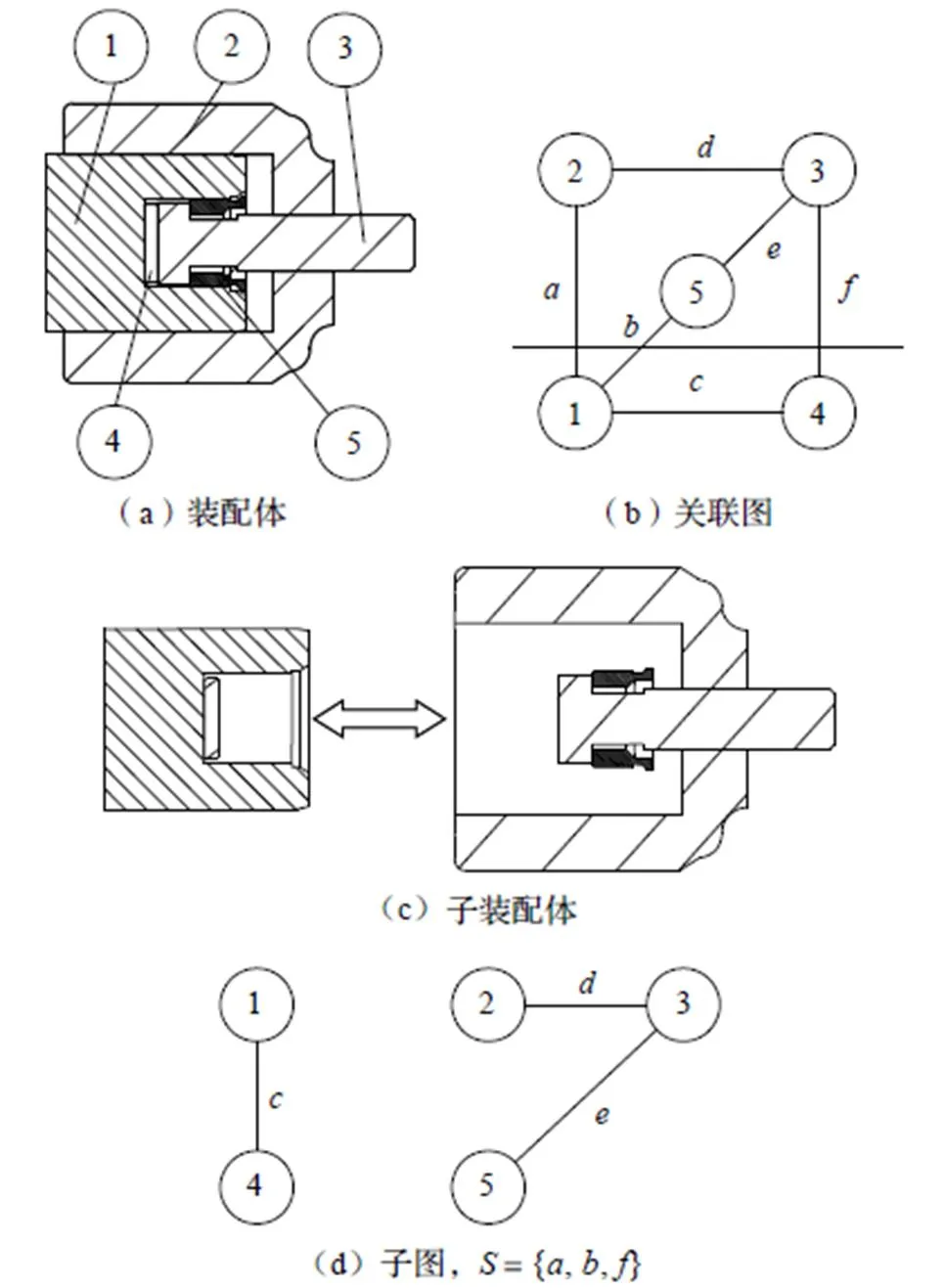
图2 装配关联图及其分解示意
1.2 简化装配模型
Baldwin等[9]通过遍历计算了装配体中的所有基本割集(装配体割集),来获取生成装配体中所有装配序列,以寻找其中的最优装配序列。判断评价每一个装配序列来寻找最优序列,会浪费大量的计算时间,因为在同一时间针对存在大量零件的复杂模型,其所需判断装配序列的数量会根据零件数量的增多呈指数级增长,导致搜索空间过大[10]。因此,有必要简化复杂模型的装配关联图、缩小需要同时进行计算的搜索空间,来达到减小计算量的目的。
单纯简化装配模型同样存在问题,并非每一次都能找到最优解。如图3所示,在缩小搜索空间的同时,很有可能同时包括了可行解的空间。最严重的情况是减小的搜索空间全部在可行解范围之内,这样很可能无法获得最佳的装配序列,导致此方法无效。减小的搜索空间不包含可行解空间的情况是一种理想情况,不是每一次都会出现。

图3 搜索空间示意图
因此,针对桁架产品的结构特点,提出了一种方法简化桁架产品以达到减小搜索空间的结果,而不影响其可行解空间:
(1)根据自上而下的方法分析其装配层次结构,得到若干个子装配体,子装配体中连接关系简单、易于规划,从而将整个模型的装配问题转化为子装配体之间的装配问题,从而达到简化整体模型的结果。
(2)将功能和尺寸都相同的连续布置的连杆聚类显示,将其表示成为连接图中的一个节点,以减少所需计算的节点。
2 使用启发式方法生成割集
使用启发式方法的流程如图4所示,主要分为三步。
2.1 启发式规则图
在这一步中,需要使用启发式方法生成规则图。在图4中,将之前连接图中零件之间的联结关系视为节点,被指向的连接必须优先完成,而指向同一连接同等级的连接则不分先后。因为在实际的产品中零件的装配过程中,某些连接总是需要优先于其他连接的先行完成;反之,在拆卸过程需要更早地解除与主体的连接。

图4 启发式方法流程图
通过启发式规则在产品的CAD数据中生成针对安装的规则图。图5显示了使用启发式规则在连接法兰中简化的螺栓连接生成规则图的示例。
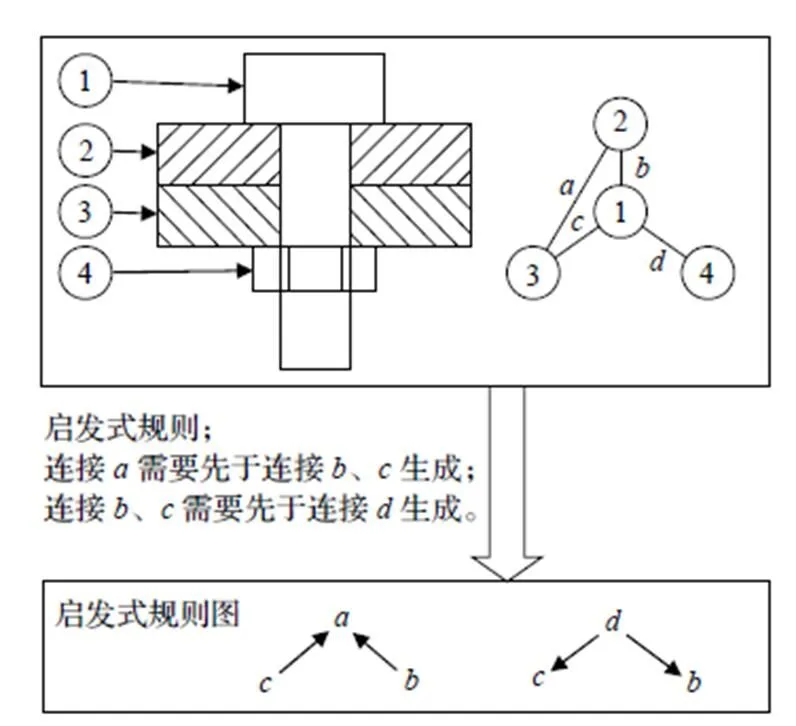
图5 螺栓连接规则图
2.2 基于层次结构的权重分配
在上一步中得到了基于启发式规则的优先图,每一个启发式优先图都是应用了启发式规则而产生的。接下来,根据得到的优先图,建立其层次结构模型。如图6所示,依据启发式规则图建立了装配体的连接优先图,以此来得到其层级结构图。每个箭头指向的连接相对具有更高的层级,而层级越高的连接就需要在装配中越早连接。
依据连接的层级结构模型,可以为每一层中的连接关系赋予权重,将权重值赋予连接关系图,将图2中的每一条连接赋予权重,得到图7。使用w来表示图中每一条边的权重,比如w=1。权重值越大的连接需要在安装过程中越早出现,反之则需要在安装过程的更后面出现。

图6 优先级图转换层次结构图

图7 连接权重赋值示意
2.3 生成树与基本割集
对连接关系赋权重的意义在于,可以依据安装过程中优先顺序的不同,对割集的质量进行评估。因此建立了评价函数Q对不同割集S进行评价,其计算公式为:
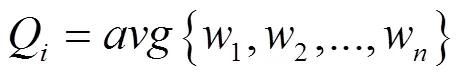
式中:w为割集S中所包含的线段的权重值;为权重值的平均值。
计算得到Q值越小,就认为其割集的质量越好,所以对于图7,其最佳割集为={,,}。
生成树是指在图中不存在环路且能遍历图中所有节点的最少边的图。获取所需要的生成树来得到连接图中的基本割集,用以生成装配序列。如图8所示,生成树可表示为={,,,},其基本割集S有四个,可计算出它们每一个割集的质量Q。
接下来根据比内-柯西定理,通过计算对应关联图的关联矩阵的子矩阵B与其子矩阵转置BT乘积的秩,就可以求解出图2连接图所对应的生成树的总数,为det(BT)=12个。如果对于每一颗生成树都进行基本割集计算,是浪费时间的,因为根据不同图的复杂程度,生成树的数量十分巨大。因此使用余树算法来进行生成树变换,以寻找其最佳生成树,从而减少计算量。

图8 生成树示意图
定义余树为=(-),其意义为在完整的连接图中去除某一生成树之后剩下的弦的集合。使用余树算法进行生成树变换可获得其最佳生成树,其算法过程如图9所示。

图9 余数算法流程图
通过使用图9的算法,就可得到连接图的良好基本割集,从而得到最佳装配序列。使用余数算法进行生成树变换的过程如图10所示。
基于最后变换得到的生成树,就可以通过值,按从小到大的顺序,将对应生成树的基本割集进行排序,依据对应基本割集在生成树中排出的零件,就可以得到对应装配体的最佳装配序列。图2所对应的装配体,其最佳装配序列为2-3-4-1-5或者2-3-4-5-1。
3 应用实例
接下来通过某型硬横跨横梁边段三维模型来验证上述方法,其结构如图11所示,结构功能相同的零件作为同一零件表示,连接图如图12所示。
根据启发式割集方法和余树算法计算其割集之后,即可得到硬横跨横梁边段的最优装配序列为:1-4-2-5-7-(6.1, 6.2)-3。
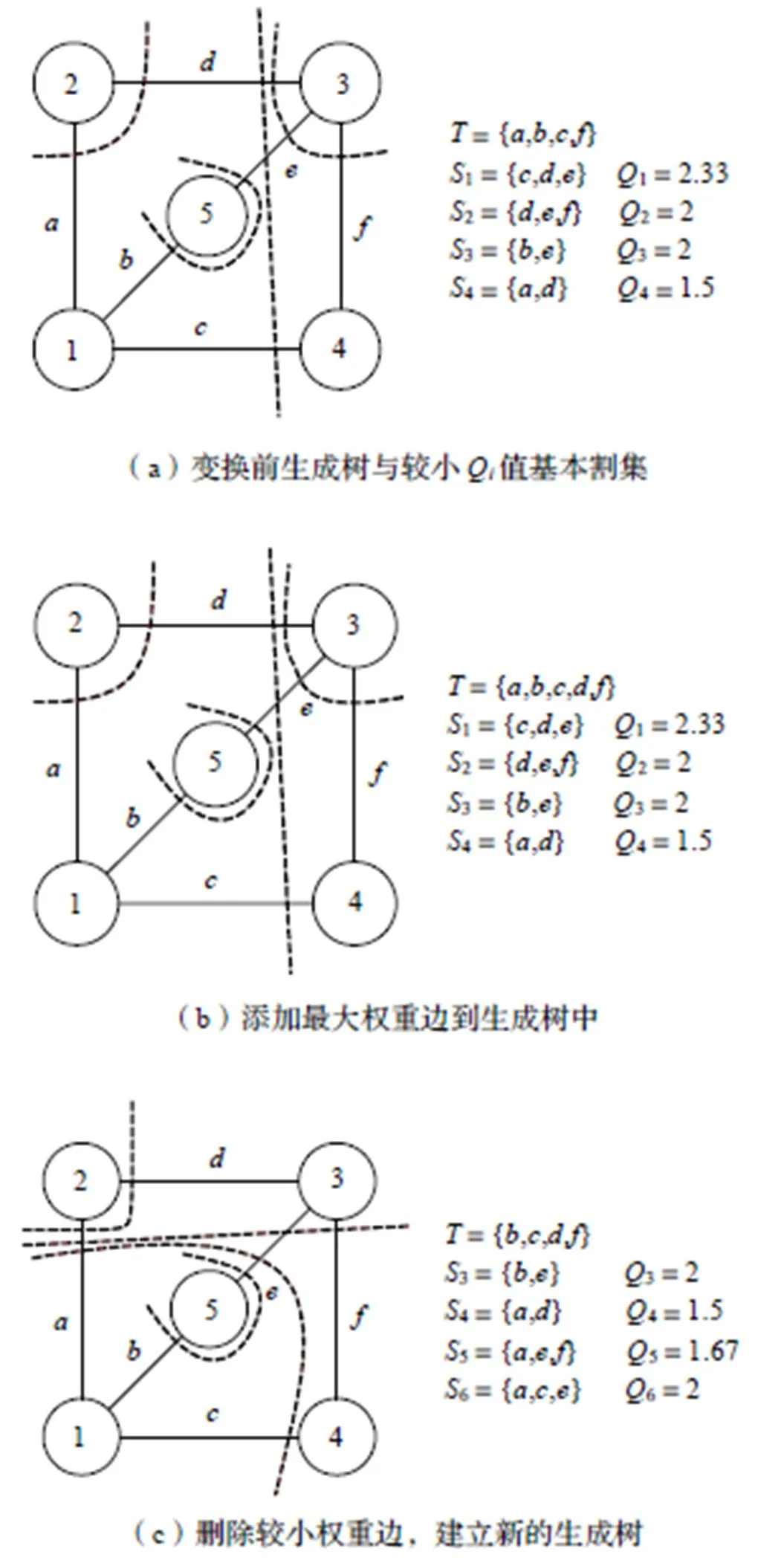
图10 余算法执行过程
4 结论
本文提出了一种基于启发式割集法的装配序列的生成方法,通过建立割集分离提取产品中的子装配体或者零件,以此来得到产品的装配序列。该规划方法的特点是通过使用启发式方法和余数算法来对关联图进行生成树变换,以获取新的良好基本割集,进而生成装配序列。实例表明,该方法可以得到良好的装配序列。
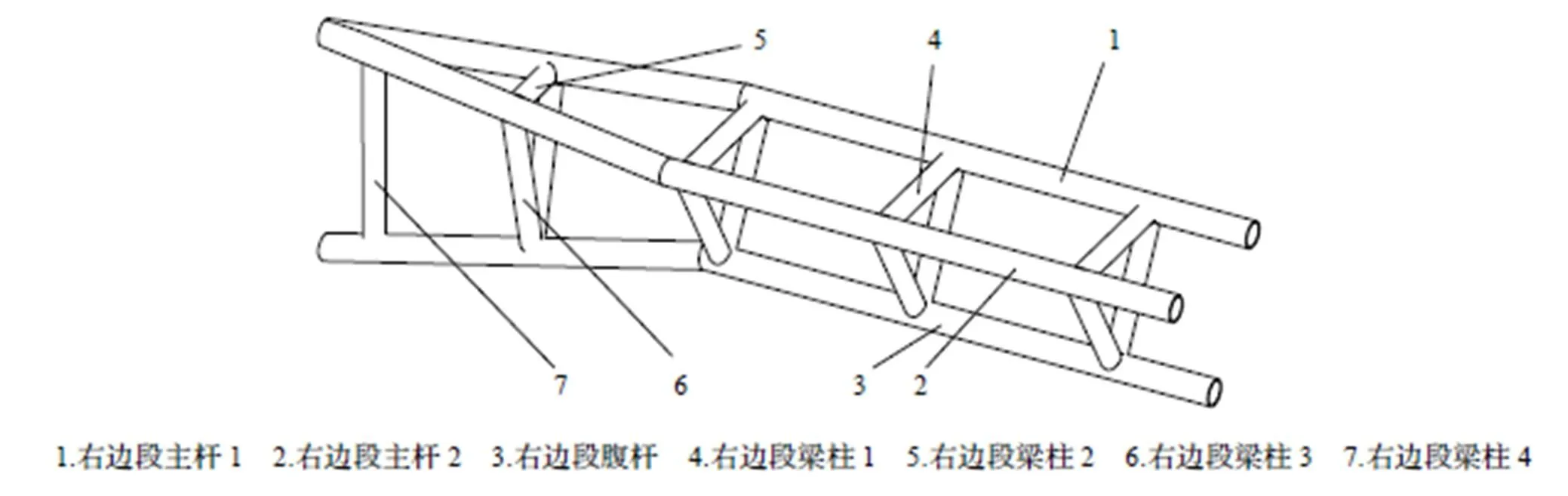
图11 硬横跨边段三维模型示意图
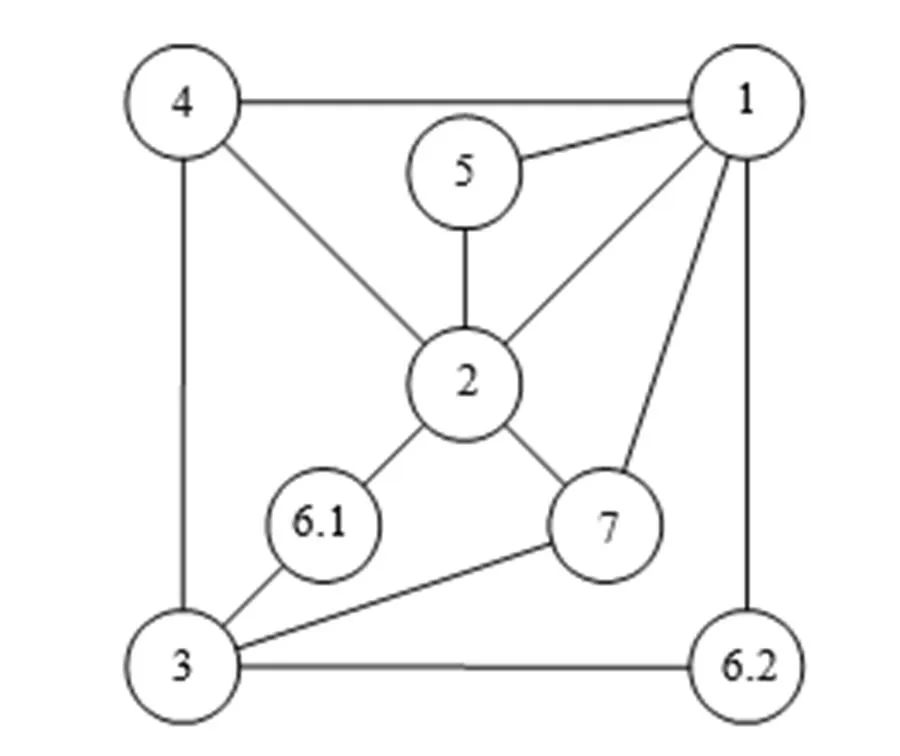
图12 硬横跨横梁边段装配关联图
[1]Womack J P,Jones D T,Roos D. The Machine That Changed the World[M]. Scribner,1991.
[2] Abdullah M A,Ab Rashid M F F,Ghazalli Z. Optimization of Assembly Sequence Planning Using Soft Computing Approaches: A Review[J]. Archives of Computational Methods in Engineering. 2019,26(2):461-474.
[3]夏平均,姚英学,刘江省,等. 基于虚拟现实和仿生算法的装配序列优化[J]. 机械工程学报,2007,43(4):44-52.
[4]付宜利,田立中,谢龙,等. 基于有向割集分解的装配序列生成方法[J]. 机械工程学报,2003,39(6):58-62.
[5]At M,Csp R. Implementation of genetic algorithm to optimize the assembly sequence plan based on penalty function[J]. ARPN J Eng Appl Sci.,2014,9(4):453-456.
[6]吴永明,戴隆州,李少波,等. 基于改进粒子群优化算法的混流装配线演进平衡[J]. 计算机集成制造系统,2017,23(4):781-790.
[7]刘晓阳,刘恩福,靳江艳. 基于蚁群算法的异步并行装配序列规划方法[J]. 机械工程学报,2019,55(9):107-119.
[8]张晶,崔汉国,朱石坚. 基于人工神经网络的装配序列规划方法研究[J]. 武汉理工大学学报(交通科学与工程版),2010,34(5):1053-1056.
[9]Baldwin D,Abell T,Lui M. An Integrated Computer Aid for Generating and Evaluating Assembly Sequences for Mechanical Products[J]. IEEE TRANSACTIONS ON ROBOTICS AND AUTOMATION,1991,7(1):78-94.
[10]De Fazio T,Whitney D. Simplified generation of all mechanical assembly sequences[J]. IEEE Journal on Robotics and Automation,1987,3(6):640-658.
Research on Truss Assembly Sequence Planning Based on Heuristic Cut Set Method
JIANG Chong,ZHANG Kai,YU Miao
( School of Mechanical Engineering,Sichuan University, Chengdu 610065,China)
At present, the design and research of truss products seldom involves its installation process. The traditional experience-based installation mode is likely to subsequently affect the installation quality of a series of modules with the same structure due to improper installation. Therefore, the installation process needs to be optimized to improve the efficiency and reliability. In this paper, a heuristic truss assembly sequence planning method based on cut set algorithm is proposed. The assembly correlation matrix is established by analyzing the model, which simplifies the assembly correlation matrix and reduces the search space of the installation sequence. Cut set method based on heuristic algorithm is used to generate assembly sequences for the assembly association graphs simplified. Finally, a single span portal structure model is used as an example to generate the installation sequence, which provides a new reference for the design of the portal structure assembly process.
truss;virtual assembly;assembly sequence planning;cut set algorithm;heuristic method
TP391.7
A
10.3969/j.issn.1006-0316.2020.05.002
1006-0316 (2020) 05-0012-06
2020-01-16
四川省科技计划重点研发项目(2019YFG0061);四川大学自贡市校地科技合作专项资金项目(2018CDZG-5);赛尔网络下一代互联网技术创新项目(NGII20180804)
姜冲(1995-),男,四川成都人,硕士研究生,主要研究方向为智能制造。*通讯作者:张凯(1984-),安徽淮南人,工学博士,助理研究员,主要研究方向为智能制造,E-mail:zkscu2005@163.com。
