环加速间隙下的脉冲星星风制动模型∗

胡永峰 仝 号

(广州大学物理与电子工程学院广州510006)

1 引言

间歇脉冲星(如PSR B1931+24)是一种只有部分时间段能够产生辐射的脉冲星子类,并且它在射电噪状态的自转减慢率(频率的一阶导数)比射电宁静状态的大∼50%[1–4].Camilo等[5]和Lorimer等[6]分别对另外的两颗间歇脉冲星PSR J1841–0500和PSR J1832+0029的分析处理也得到类似的结果. 这表明间歇脉冲星不同的辐射模式对应不同的自转模式, 即其自转与辐射之间存在联系.

蟹状星云脉冲星(以下简称Crab脉冲星)是一颗频率ν=30.2 Hz, 长期观测的制动指数平均值n=2.51 (n的定义为)的年轻射电脉冲星[7]. 假设脉冲星的制动机制为经典的纯磁偶极制动, 即在真空中以频率ν自转的中子星, 具有磁矩µ, 对应的自转减慢率为[8]

其中磁矩大小µ=BR3/2,B是脉冲星表面的磁感应强度大小,R是脉冲星半径(取典型值R=106cm),I是转动惯量(取典型值1045g·cm2),c是光速,α是磁倾角(脉冲星磁轴和自转轴的夹角), 这个可以简写成3. 当考虑脉冲星的磁倾角、转动惯量、磁场强度不发生变化时, 那么可以得到制动指数n等于3. 但是根据已观测到一些脉冲星的制动指数的结果中发现, 制动指数n基本上都在1–3之间[9–16], 这意味着脉冲星的制动机制不是简单的磁偶极制动.

Xu等人提出星风制动模型: 脉冲星的制动等于粒子风制动加上磁偶极制动, 并且其中粒子风制动依赖于不同的加速电势(由脉冲星磁层的加速间隙提供)[17]. 在星风模型的框架下, 脉冲星的磁层中存在大量的带电粒子. 这些粒子在强磁场中一方面通过加速过程会产生辐射, 另一方面这些粒子会带走脉冲星的一部分转动能, 从而起到制动的作用(辐射源于转动能). 因此, 星风模型可以很好地同时解释脉冲星的辐射、自转、制动指数不等于3等问题, 即上面关于间歇脉冲星和Crab脉冲星观测中存在的问题.

星风模型依赖于不同的加速间隙模型. Li等[18]在基于Xu等[17]提出的星风模型基础上, 通过建立在真空加速间隙和外加速间隙等情形下的星风模型, 计算得到间歇脉冲星PSR B1931+24在射电噪和射电宁静状态下的自转减慢率之比依赖于不同的加速间隙类型和磁倾角, 并且计算得到其磁场强度和磁倾角以及理论预言的制动指数[18].Kou等[19]在基于Xu等[17]提出的星风模型基础上进行拓展, 考虑了粒子密度效应和死亡效应下的星风模型.

本文旨在基于Li等[18]及Kou等[19]工作的基础上进行拓展, 把环加速间隙运用于星风模型中. 建立了同时考虑具有不同加速电势的核区和环区的环加速间隙下的星风模型,去解释间歇脉冲星PSR B1931+24的观测结果和模拟Crab脉冲星的自转演化. 本文的结构如下: 第2节介绍环加速间隙下的脉冲星星风模型; 第3节和第4节介绍模型的应用;第5节和第6节是讨论和总结.

2 环加速间隙下的脉冲星星风模型

2.1 环加速间隙

通常认为: 脉冲星的磁层中充满了带电粒子, 并且是正负电荷分离的情形. 磁层区域包括闭合磁力区和开放磁力区. 在闭合区带电粒子随脉冲星共转, 处于静态磁层情形, 不能产生辐射, 而在开放区带电粒子有外流并且会在加速过程中产生辐射. 对于开放磁力区(极冠区), 临界磁力线把它划分为电荷异号的靠近磁轴的核区和靠近最后一根开放磁力线的环区(参考Qiao等人工作的图1[20]). 整个极冠区的半径为rp=R(RΩ/c)1/2, 其中核区的半径为rcore=(2/3)3/4R(RΩ/c)1/2≈0.74rp[21], 所以环区的半径为rann=rp−rcore≈0.26rp. 由于核区和环区的半径大小都正比于角速度Ω(结合下面的(3)式分析可知它们的星风强度也正比于角速度), 所以这种情形更适用于角速度比较大的脉冲星. 比如年轻的脉冲星, 而对于年老的角速度比较小的脉冲星则可以忽略[22].

Qiao等人通过对PSR J0815+09建立核区和环区间隙共存的模型, 合理地解释了传统间隙模型不能解释清楚的脉冲星子脉冲双向漂移现象[23]. 环区间隙可以很好地模拟脉冲星的射电辐射和伽马辐射性质[24]. 对于脉冲星磁层的加速区域需要同时考虑核区和环区都加速的情形, 在环区和核区都可以加速带电粒子, 并产生初级粒子和次级粒子外流以产生多波段的辐射. 相比于脉冲星的极冠间隙和外间隙, 环区间隙同时结合了这两者的优点[20]. Du等人通过运用核区间隙和环区间隙对Vela脉冲星的辐射进行模拟, 得到其伽马射线轮廓的峰值p1和p2来自于靠近零电荷面的环区, 峰值p3和桥辐射来自于核区, 而射电辐射则来自于环区比较高的狭窄区域[22]. 这表明环区间隙也是脉冲星的一种适宜的加速间隙, 可以同样考虑运用于星风模型中. 下图(见图1)为脉冲星极冠的环区示意图, 其中虚线圆包围的区域为核区, 虚线圆到实线圆之间的区域为环区.

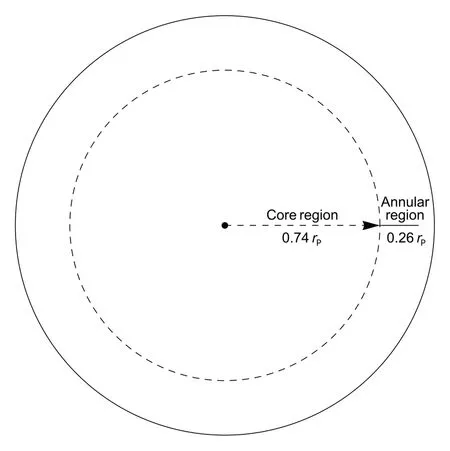
图1 脉冲星环间隙的示意图Fig.1 Sketch for annular gap of pulsars

2.2 环加速间隙下的星风模型

根据Xu等人提出的星风制动模型: 对一个斜转子的脉冲星来说, 脉冲星自转能损的能量等于脉冲星磁矩的垂直分量(µ⊥=µsinα)主导的磁偶极辐射的能量加上脉冲星磁矩的平行分量(µ∥=µcosα)主导的加速粒子的能量[17], 可以简称脉冲星的制动等于磁偶极制动加上粒子风制动, 即. 对于磁偶极制动部分可以写成[8]

其中Ω=2πν为脉冲星的角速度. 而对于粒子风(也可称星风)制动的部分可以写成[17]

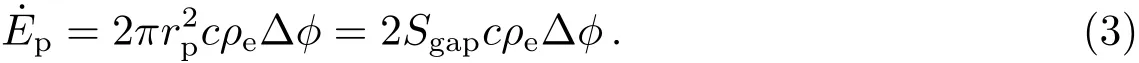
其中ρe=κρGJ(ρGJ=ΩB/(2πc)是Goldreich-Julian电荷密度)[25],κ是初始粒子密度系数,Sgap是加速间隙的面积, ∆ϕ是间隙的加速电势. 不同间隙的加速电势不同, 星风模型依赖于不同的加速间隙.

对于脉冲星磁层中带电粒子的加速间隙, 需要同时考虑到核区的加速间隙和环区的加速间隙[20], 而不仅仅只是某一种单一的加速间隙. 因此本文建立同时考虑了核区的加速电势取∆ϕVG(CR)(VG(CR)代表在真空间隙中的相对论性初始电子通过曲率辐射产生伽马射线)[17], 以及环区的加速电势取∆ϕ=0.5ΩBr2pc−1[26]的环加速间隙下的星风模型情形, 下面是具体的计算过程.

对于核区的星风成分有: 核区的面积为Scoregap=π(0.74rp)2,∆ϕcore=∆ϕVG(CR)=9.2×1010, 其中(B的单位为Gs). 代入(3)式化简得:

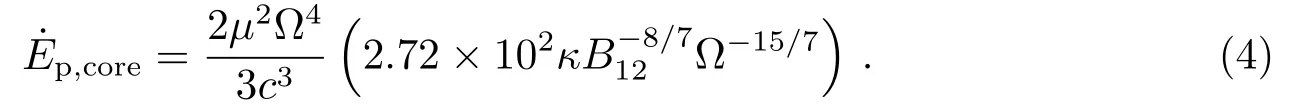
对于环区的星风成分有:Sanngap=π[r2p−(0.74rp)2]. 而∆ϕ=0.5ΩBr2pc−1代入相关参数可以化简为sin2θp, 其中θp是脉冲星极冠区的最大张角. 因为这个是脉冲星极冠区的最大加速电势, Qiao等人指出脉冲星磁层中环区的加速电势要依赖于其极冠区的最大加速电势[26], 再结合图1, 最终考虑环区的加速电势为∆ϕann=其中θp,core=0.74θp,θp≈sinθp=为光速圆柱半径), 代入(3)式化简得:

考虑到星风成分主要由磁矩的平行分量µ∥=µcosα主导, 故上面核区和环区的星风成分加上一个cosα权重因子. 综上, 脉冲星的自转能损率等于:

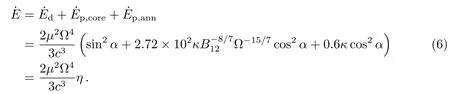
其中η=sin2α+2.72×102κB−8/712Ω−15/7cos2α+0.6κcos2α为环加速间隙下的星风模型的无量纲化η因子.

3 模型的应用–间歇脉冲星PSR B1931+24

对于间歇脉冲星PSR B1931+24来说, 其脉冲星自转能损率的表达式为:=−IΩ. 它在射电噪状态的制动为磁偶极制动加上星风制动, 而在射电宁静状态的制动只有磁偶极制动[18]. 两种状态下的自转能损率分别为

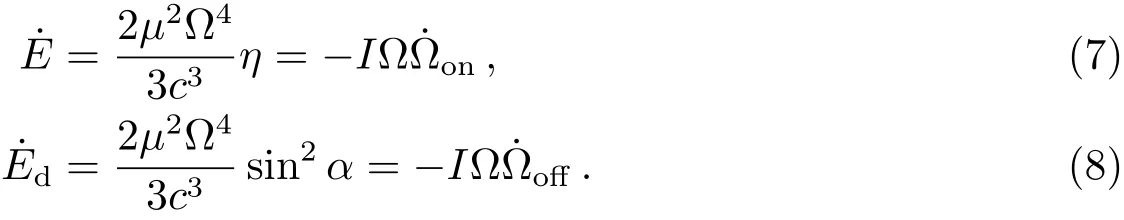
根据上述计算得到

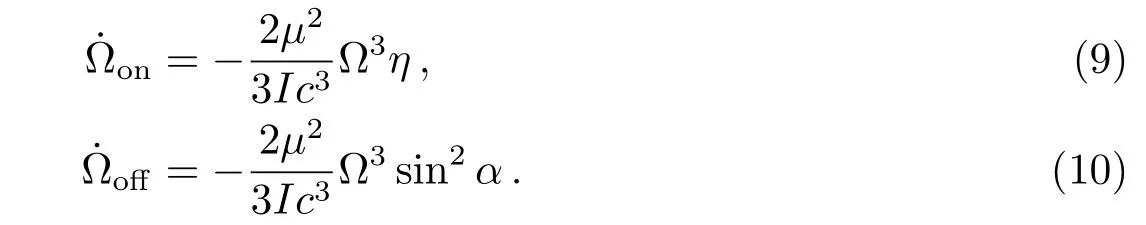
(10)式代入相关参数可以简化为

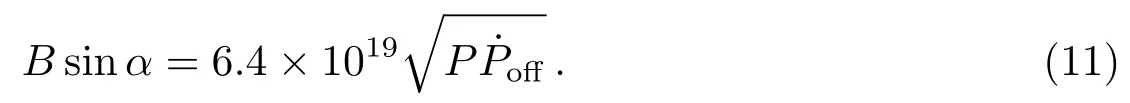
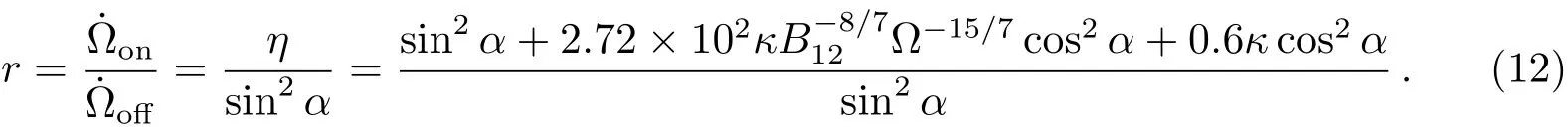
再根据上面计算出来的η因子, 可以得到间歇脉冲星PSR B1931+24在两种状态下自转减慢率的比律r为根据观测到间歇脉冲星PSR B1931+24的ν=1.2 Hz、off=−10.8×10−15Hz·s−1、on=−16.3×10−15Hz·s−1[1], 并计算出. 为了与Li等人的结果进行比较, 也取κ=1[18]. 然后联立(11)式和(12)式求解得到磁场强度B=5.9×1012Gs与α=55◦. 将得到的B代入(12)式, 得到r关于磁倾角α的函数关系并画出图像(见图2). 图中虚线代表PSR B1931+24观测到的r值1.5, 从图中可以看出, 随着磁倾角α的增大, 间歇脉冲星PSR B1931+24在射电噪与射电宁静状态下自转减慢率的比律r渐减小, 这是因为r近似∝(1+cot2α).

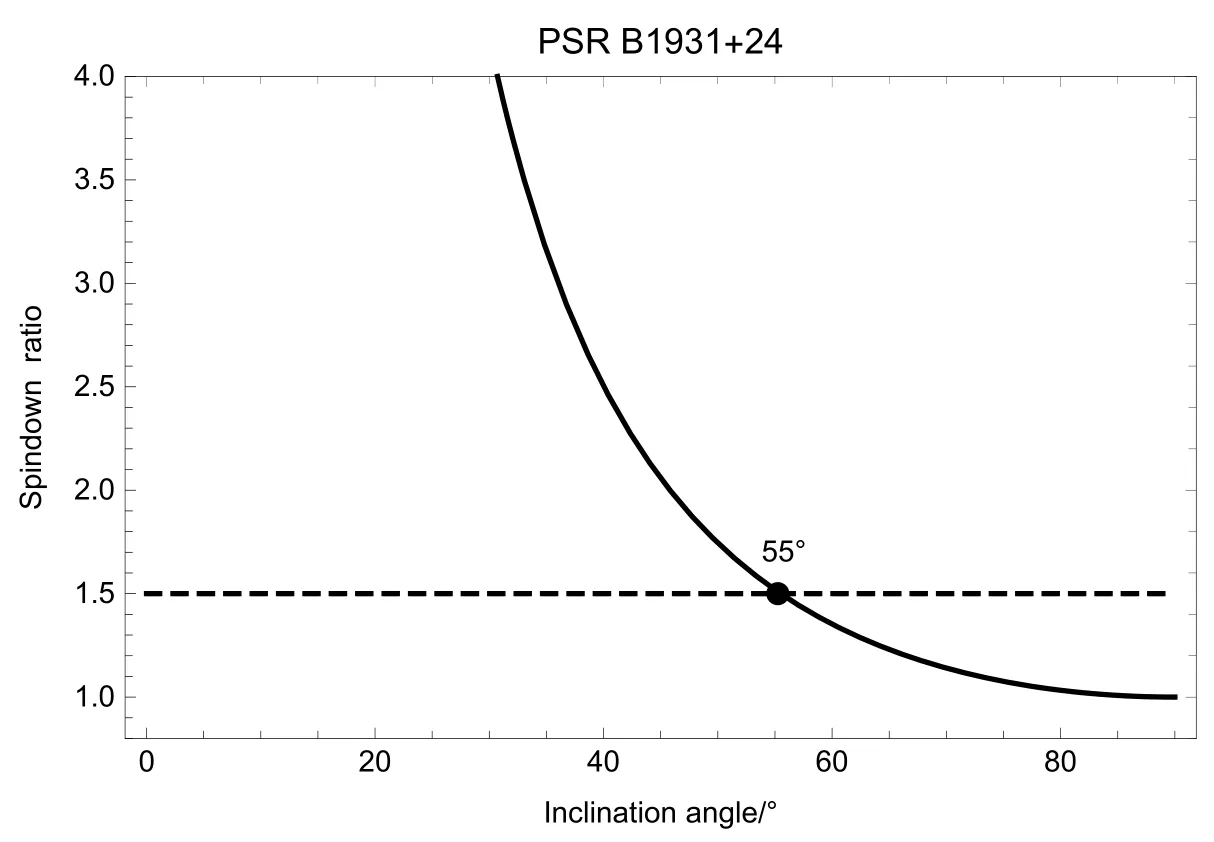
图2 PSR B1931+24的自转减慢率关于磁倾角的函数关系Fig.2 Spindown ratio of PSR B1931+24 as a function of inclination angle

间歇脉冲星PSR B1931+24在射电宁静的状态下只有磁偶极制动, 根据第1节分析可知其制动指数noff=3. 而在射电噪的状态下, 其制动指数n为[17]

再代入前面计算出的η值得到

将上面计算出的磁场强度B代入(14)式, 即可以得到制动指数n关于磁倾角α的函数关系并画出图像(见图3). 从图中可以看出, 随着磁倾角的减小, PSR B1931+24在射电噪状态下的制动指数从3逐渐趋向于2. 这是因为随着磁倾角α的减小, 脉冲星的制动成分(见(6)式)中, 磁偶极制动(∝sin2α) 不断变弱, 而粒子风制动(∝cos2α)则逐渐占主导.在当前计算出来的磁倾角α=55◦下, 所预言的制动指数n=2.7.

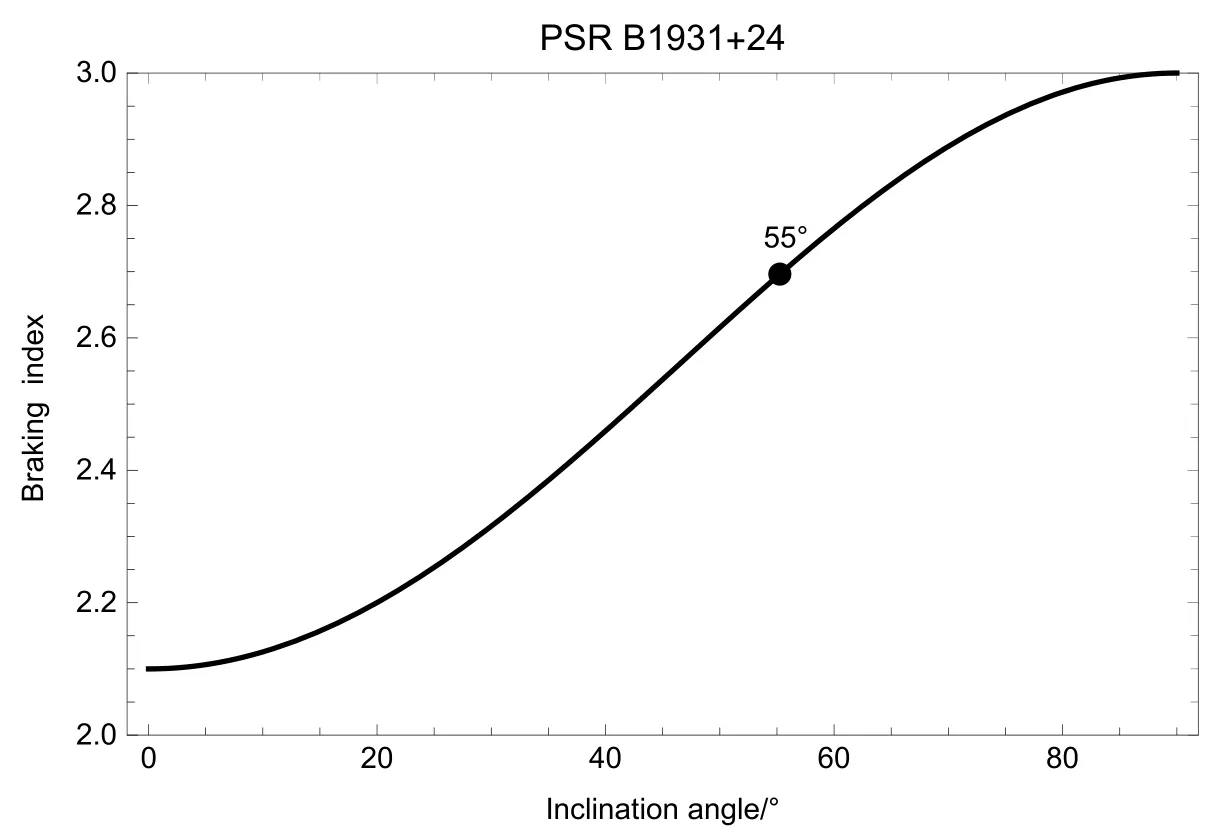
图3 PSR B1931+24的制动指数关于磁倾角的函数关系Fig.3 Braking index of PSR B1931+24 as a function of inclination angle

4 模型的应用–Crab脉冲星

4.1 制动指数随周期的演化

对于Crab脉冲星, 其自转减慢率可以写成:

其制动指数的表达式同(13)式一样. 其二阶制动指数m为[19]:

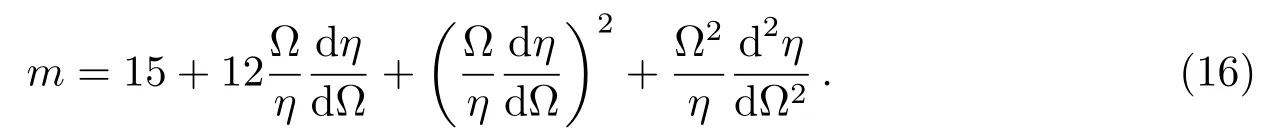
根据对Crab脉冲星的观测数据有:ν=30.2 Hz、=−3.86228×10−10Hz·s−1、n=2.51、m=10.15、年龄为915 yr (AD1054—1969)[19]. 运用这些数据, 理论上根据(13)、(15)与(16)式就可以解出α、B、κ, 但这里涉及到高阶的非线性项, 比如cosα、sinα. 为了与Kou等人的结果进行比较, 也取κ=1000[19]. 然后把Crab脉冲星的观测值ν、、n直接代入(13)与(15)式中进行联立求解α与B, 发现得不到精确的数值解. 通过分析(6)式得到: 磁偶极成分d∝Ω4, 核区星风成分p,core近似∝2.72×102κΩ2, 环区星风成分p,ann∝κΩ4. 对于Crab脉冲星来说, 当取κ=1000时, 环区的星风成分相对于磁偶极成分和核区的星风成分都太强了. 故考虑环区的加速电势为经典常加速电势的情形: ∆ϕann=3×1012V, 则重新计算得到:

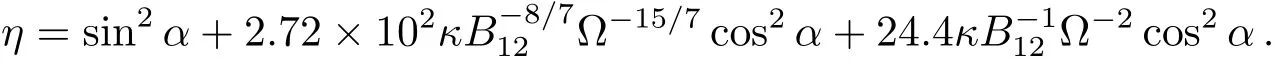
再重新联立(13)与(15)式求得α=48◦与B=8.9×1012Gs, 其中α符合观测模拟出来的结果45◦–70◦[27–31]. 然后把计算得到的α与B代入(16)式进行检验得到m=10.94与观测值10.15非常接近, 考虑观测的不确定性可以认为取κ=1000是可以的. 最后再把这一计算得到的α与B代入(13)式中, 则可以得到n关于Ω的函数关系, 转换一下即得到制动指数n关于周期P的函数关系并画出图像(见图4). 图中虚线代表观测到的制动指数2.51,点划线代表过渡制动指数2. 从图中可以看出, 脉冲星制动指数随着其自转周期的增大从3演化到1, 这与已观测到制动指数的一些脉冲星的观测结果很接近.

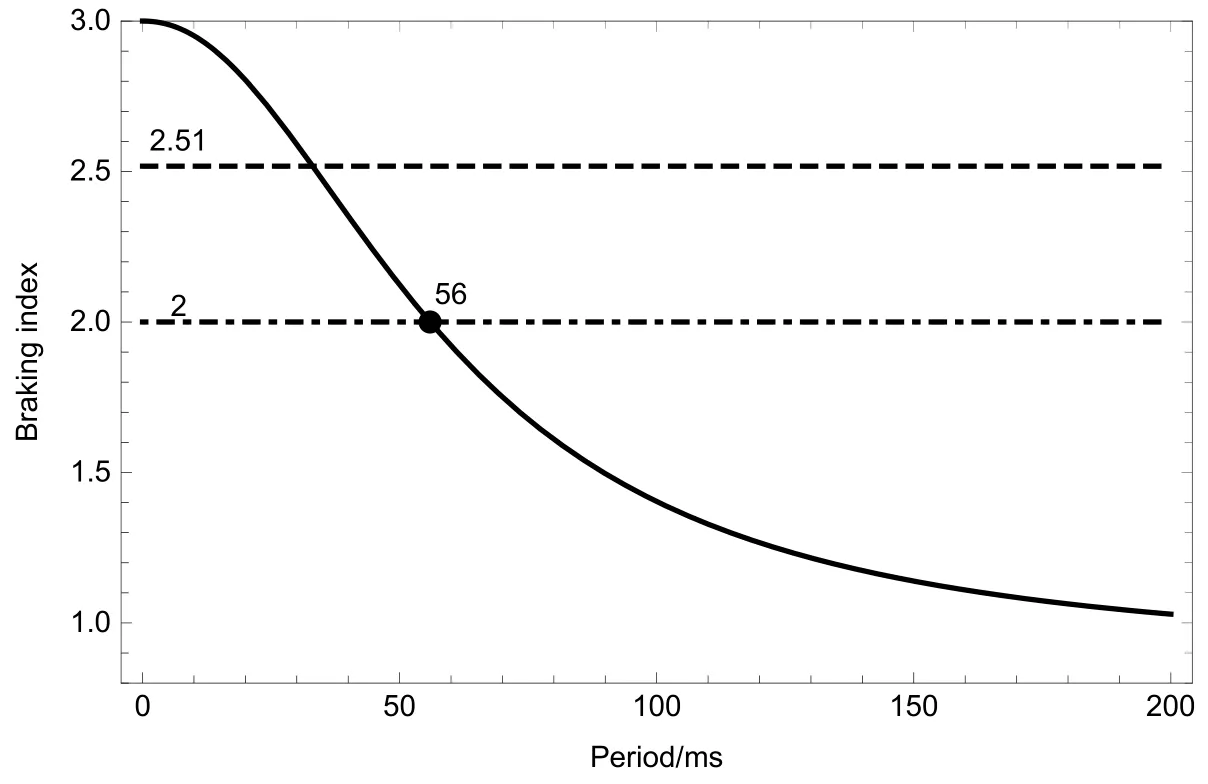
图4 Crab脉冲星的制动指数关于周期的函数关系Fig.4 The braking index of the Crab pulsar as a function of spin period

根据上面的η因子的表达式可知磁偶极制动成分为sin2α∝Ω4, 星风制动成分为(2.72×102κB−8/712Ω−15/7cos2α+24.4κB−112Ω−2cos2α)近似∝Ω2. 由Ω4比Ω2更高阶的幂指数很明显看出Crab脉冲星在前期角速度很大的时候, 磁偶极制动相比于星风制动占优, 只有到后期随着自转角速度越来越小, 星风制动才会逐渐占优. 其中磁偶极制动对应的n=3, 星风制动对应的n=1.

4.2 Crab脉冲星的短期和长期自转演化

将上面计算得到的α与B代入(15)式得到关于Ω的一阶微分方程. 根据Crab脉冲星的年龄915 yr, 直接对(15)式积分求得初始周期P0=18.8 ms, 进而求出初始角速度. 再求解这个微分方程得到Crab脉冲星的角速度Ω关于时间(年龄)的函数,转换一下得到周期P和周期导数关于年龄的函数. 取制动指数n=2为Crab脉冲星在磁偶极制动和星风制动相互平衡时的过渡点, 将上面计算得到的α、B代入(13)式中得到n关于Ω的函数, 代入n=2并求解得到过渡周期Pt=56 ms (见图4中的黑色点). 再把过渡角速度代入(15)式进行积分计算得到过渡年龄Tt=2810 yr. 最后将一系列离散的包括Tt在内的年龄数值代入上面P和分别关于年龄的函数中, 转换一下即得到P关于的函数关系并画出图像(见图5的细实线, 本图从Tong等[32]中更新). 从细实线上发现过渡点刚好为线上的最低点(见细实线上的大黑色圆点), 再结合图4可以得到过渡点为Crab脉冲星在P-图上自转演化的拐点, 而在拐点的两侧分别对应为Crab脉冲星磁偶极制动占优和星风制动占优的情形.

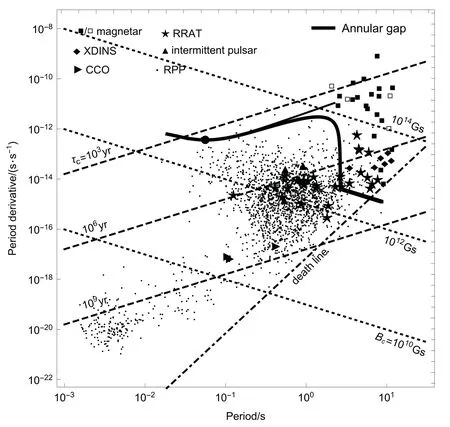
图5 Crab脉冲星在环间隙下的自转演化. 细实线为没有考虑死亡效应的演化, 粗实线为考虑死亡效应的演化. 图中展示了各种类型的脉冲星(从Tong等[32]中更新), magnetar: 磁星(空心方框是有射电辐射的磁星), RRAT: 旋转射电暂现源, XDINS: X射线暗的孤立中子星, intermittent pulsar: 间歇脉冲星, CCO: 中心致密天体, RPP: 自转供能脉冲星.Bc是特征磁场, τc是特征年龄. 点划线代表基准死亡线[21].Fig.5 Rotational evolution of the Crab pulsar in the annular gap. The thin solid line is the evolution without considering the death effect, and the thick solid line is the evolution considering the death effect.The figure shows various types of pulsars (updated from Tong et al.[32]), magnetars (empty squares are magnetars with radio radiation), RRAT: rotating radio transients, XDINS: X-ray dim isolated neutron stars, intermittent pulsar: intermittent pulsars, CCO: central compact objects, and RPP: rotation powered pulsars. Bc is the characteristic magnetic field, τc is the characteristic age. The dot-dashed linerepresents the fiducial death line[21].

另外从图5的细实线可以看出Crab脉冲星最终会演化为磁星. 但这与观测不符,因为磁星的数量比一般的脉冲星少很多, 而且大多数脉冲星居于P-图(见图5)中间的区域[19]. 因此, 对于Crab脉冲星的长期演化则需要考虑死亡效应. 所谓死亡效应就是指当脉冲星的自转角速度不断降低时, 从脉冲星能够获得的最大加速电势∆Φ=µΩ2/c2∝Ω2会不断减小并最终要小于所需要的加速电势要求, 继而最终停止辐射, 脉冲星则走向死亡[21]. 根据Kou等人对Crab脉冲星死亡效应下的η因子计算结果[19], 本文对这个死亡效应下的η因子调整为:

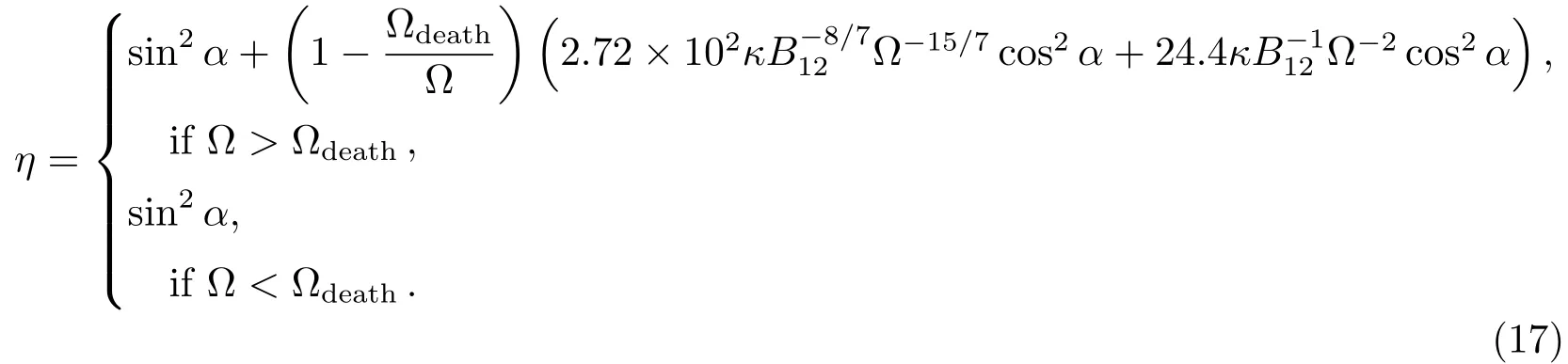
其中Ωdeath=2π/Pdeath,Pdeath=2.8

取Vgap=1013V[33], 把上面计算得到的B代入上式得到死亡周期Pdeath=2.64 s, 以及计算得到死亡年龄Tdeath=1.6×106yr (与上面计算Tt方法类似). 计算Crab脉冲星在死亡效应下的长期自转演化与上面计算不考虑死亡效应方法相类似. 最终结果见图5的粗实线. 脉冲星的自转演化可以描述为:=−kνn(k为常数)即(2−n), 对应在P-图上演化路径的斜率为2−n[14]. 从粗实线可以看出Crab脉冲星在从开始短期内的演化磁偶极制动(n=3)占优情形(斜率为−1), 逐步演化到星风制动(n=1)占优情形(斜率为1), 到后期随着角速度越来越慢, 辐射会越来越弱直至停止. 最终Crab脉冲星在P-图上不会演化为磁星, 而是直接往死亡线的方向演化. 汇总一下上面所计算的结果(见表1).

表1 环间隙下Crab脉冲星计算得到的参数Table 1 Calculated parameters of Crab pulsar in the annular gap

5 讨论

5.1 间歇脉冲星的间歇性星风

对于间歇脉冲星PSR B1931+24周期性的间歇状态, 前人做了很多工作. 比如: PSR B1931+24在射电宁静状态磁层中由于缺少粒子流, 导致相比于射电噪状态没有射电辐射和更小的自转减慢率[1]. PSR B1931+24周围有一个来自于超新星遗迹或者星际介质的物质盘在进出光速圆柱时, 会中断和重启脉冲星的辐射并且对应为两种不同自转减慢率的状态[35]. PSR B1931+24是轻微的在死亡线以下的脉冲星偶然恢复辐射, 或者是与消零脉冲星视线方向相反的情形[36]. 基于星震理论下的非径向振动模型解释PSR B1931+24自转减慢率出现的周期性涨落[37]. 脉冲星进动导致磁层状态发生改变的模型[38]. 以及Huang等[39]提出间歇脉冲星PSR B1931+24的磁层极冠区的局部区域存在超强磁场, 这一超强磁场会导致其极冠区周围的局部外壳层发生长期的活动, 继而引起了闭合磁力区的磁层发生扭曲. 导致其中很多的磁力线由之前闭合的状态转换为打开的状态, 从而增大了会产生辐射的开放磁力区面积, 辐射亦即变强, 并最终增大了脉冲星的自转减慢率(辐射能来源于转动能). 这种扭曲状态在一定扭曲角度范围内可以保持稳定,但当其扭曲角度达到最大值时, 由于磁流体力学的不稳定性, 会发生解扭过程. 则闭合磁力区的磁层又重新回到了原先的关闭状态, 并且相应的自转减慢率也减小到原来的水平. PSR B1931+24这种周期性的间歇状态就是由于其闭合磁力区的磁层发生了周期性的扭曲和解扭过程导致的[39].

5.2 核区和环区的星风强度

5.3 脉冲星的星风强度

对于同一个脉冲星来说, 它在短时标内的Ω几乎不变, 而它的磁场强度B与磁倾角α在星风模型的框架下又是计算出来的定值(围绕脉冲星可以被观测到的磁倾角α和制动指数n去建立星风模型和检验星风模型, 而不考虑B与α变化). 所以对于同一个脉冲星而言, 其星风强度主要是由粒子密度来决定的, 而其星风强度发生变化也主要是因为其磁层中粒子密度发生变化导致的. 比如间歇脉冲星PSR B1931+24, 它在射电噪状态的粒子密度系数κ为1, 磁层中有星风且强度可以通过上面的式子计算出来. 而它在射电宁静状态的粒子密度系数κ为0, 磁层的星风强度也为0.

而对于不同脉冲星的星风强度差异, 一般来说它们磁场强度B的大小都约为典型值1012Gs附近, 磁倾角α的差异也不会太大. 另外一方面, 磁场强度B12的指数为−8/7,角速度Ω的指数为−15/7, 几乎是前者的2倍, 而且要加上考虑到不同脉冲星角速度的差异也很大, 再加上不同脉冲星磁层的粒子密度不一样, 这样就会导致最终不同脉冲星的星风强度差异更大. 比如间歇脉冲星PSR B1931+24和Crab脉冲星, 它们磁层的粒子密度相差1000倍, 角速度相差约25倍, 导致其星风强度差异很大就是这种情形. 虽然后面因为Crab脉冲星的环区星风太强而考虑其环区为常加速电势的情形, 得到了新的星风强度表达式. 但是通过计算出来的核区和环区磁场强度B12的指数分别为−8/7和−1, 仍然只是约为角速度Ω指数的一半. 所以, 不同脉冲星的星风强度差异主要是由其角速度Ω和粒子密度的差异造成的.

5.4 粒子密度

在星风模型下, 计算出来的Crab脉冲星和间歇脉冲星PSR B1931+24的磁倾角α和磁场强度B差不多, 但Crab脉冲星的磁层粒子密度却是PSR B1931+24的1000倍, 这可能是因为Crab脉冲星的角速度Ω更大的原因造成的. 从数学角度讲: 星风制动模型下的η=sin2α+2.72×102κB−8/712Ω−15/7cos2α+0.6κcos2α(其中第1项sin2α代表磁偶极制动项的η因子, 第2项代表核区星风项的η因子, 第3项代表环区星风项的η因子), 角速度越大, 对应核区星风成分(∝Ω−15/7)会越弱. 间歇脉冲星PSR B1931+24的角速度比Crab脉冲星小约25倍, 如果Crab脉冲星的粒子密度也和PSR B1931+24的粒子密度一样κ=1, 则会严重降低其核区的星风成分强度(这里不考虑公共项). 所以这种情形下最好把粒子密度增大(不考虑降低B12)以提高核区的星风成分强度才行. 又因为环区星风成分的η因子与角速度Ω无关, 所以如果把粒子密度增大1000倍, 则又会严重增大环区的星风成分强度, 使其最后得不到精确的数值解. 故对于Crab脉冲星来说其环区的加速电势取为经典常加速电势: ∆ϕann=3×1012V. 从某种程度上讲, 这可能意味着对于不同转速的脉冲星, 由于从脉冲星能够获得的最大加速电势∆Φ=µΩ2/c2∝Ω2[21].所以角速度越大, 脉冲星由于单极感应[17]产生的加速电势会越强, 继而导致磁层中的粒子密度越大, 最后辐射也越强.

综上, 环加速间隙也同样能够适用于星风模型的框架. 同一个脉冲星的星风强度发生变化主要是由于其磁层中粒子密度发生变化导致的. 不同脉冲星星风强度的差异主要是由其角速度Ω和磁层中粒子密度的差异造成的, 并且脉冲星角速度的大小可能是与粒子密度正相关的一个因素.

6 总结

相比于真空加速间隙、外加速间隙等下的星风模型, 环加速间隙也同样能够适用于星风模型. 本文建立了同时考虑具有不同加速电势的核区和环区的环加速间隙下的星风模型, 运用此模型来解释间歇脉冲星PSR B1931+24和Crab脉冲星的观测, 主要结论如下:

(1)对于间歇脉冲星PSR B1931+24: 射电噪状态下额外的粒子风制动导致其在射电噪状态下的自转减慢率比射电宁静状态下的要大. 利用观测到的两种状态下自转减慢率的比律, 计算得到磁倾角α=55◦和磁场强度B=5.9×1012Gs, 并且预言了其理论的制动指数n=2.7, 未来望远镜对间歇脉冲星PSR B1931+24制动指数和磁倾角的观测可以用来检验这个模型;

(2)对于Crab脉冲星: 计算得到其磁倾角α=48◦和磁场强度B=8.9×1012Gs. 得到其制动指数n随着周期P的增大从3演化到1, 并计算得到它在P-图上的自转演化.