基于“哈密顿模型”的线性规划在汽配件生产排程问题中的应用

李泽萱 闵慧旭 骆秋荣 林道荣 唐日成 张海飞

摘要：该文基于有向哈密顿图回路模型，对于汽车零配件的排程进行合理规划，该过程通过MATLAB程序实现了线性规划问题数学模型的求解方法，并进一步通过实例模型求解方法的分析比较，证明所采用的程序方法有效快捷。文中的程序简单明了且具有通用性，只需输入规划模型中对应的相关矩阵，立即得到最优解和最优值。

关键词：哈密顿有向图模型;周期等量;线性规划;最优解;最优值

中图分类号：TP391 文献标识码：A

文章编号：1009-3044（2020）10-0248-04

1背景

在汽车零件的生产过程中，需要对不同类型的零件进行喷漆上色，而在喷漆的过程中，由于仅有有限个喷漆装置，而对于不同颜色的喷漆，需要进行换色，在换色过程中便不免会产生消耗，如果因为在不同圈中相同编号滑橇上摆放的零件种类发生变化时需要人工进行更换对应支架，为了减少人工负担，尽可能换色的次数减少。因此需要对零件进行排程，针对已知的指导生产量制定出生产线未来八圈的详细喷涂排序计划，不仅要为了降低生产成本减少换色的次数，并尽可能地满足指导生产量的需求（可以允许超过计划生产量的产出，但不会带来额外的直接收益）。

2问题分析

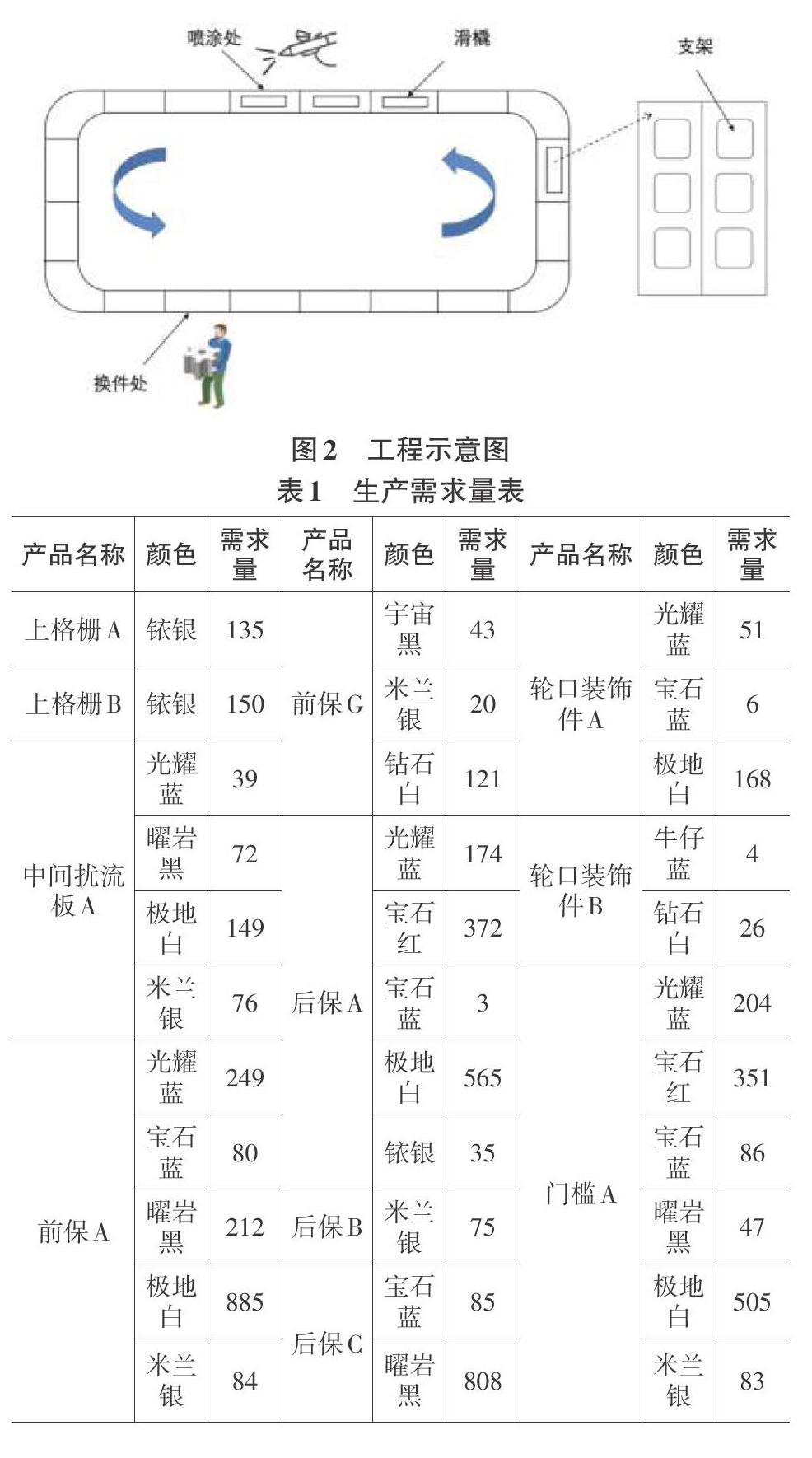
某汽车零配件制造商的生产流程如下图1：生产流程图所示，其中注塑环节完成的汽车零件经过火焰烘烤和人工处理后进入注塑件缓存区准备进行喷涂。喷涂过程如图2：工程示意图所示，在传送带上完成，传送带轨道.上装有滑橇，滑橇上装有可拆卸支架，每个零件需要放在特定的支架上进行顺序喷涂。喷涂过程的一个生产周期称作“一圈”（即将传送带轨道.上所有滑橇上的零件喷涂完毕），一圈共有303个滑橇，全部喷涂完毕的时间大概在5.5个小时，一个滑橇喷涂工序节拍大概在1分钟。一个滑橇有两面，可同时喷涂，一面可以放3个支架，一个滑橇共可放6个支架，支架类型与零件种类为一一对应关系，每种零件只能放置在对应的特定支架上。一个滑橇上只放置同种零件，滑橇不强制要求摆满支架和零件，但为避免产能浪费，无特殊原因不会放空支架。支架的数量是有限制的，所以在一圈的生产计划中同种零件的上架数也有对应上限。

3模型建立

3.1数据处理

根据表1：生产需求量表所示，表l中提供的数据是按照颜色进行分类，即同种颜色的不同产品按照需求量降序的形式在表1里排列出来，为了达到换色次数要尽可能少的目的，所以将需求量最大的（例如产品为前保D颜色为曜岩黑的零件需求量为992个，将其除以6向上取整约为166个滑橇，则在一维数组前166个空间放人166个曜岩黑滑橇）放在形如一维数组（长度8*303）的最前面，在对同种颜色的配件进行处理，当同一种颜色的配件全部处理完后再处理下一个颜色，同时为了保证符合题干中给出的约束条件，即先满足每个滑橇中的6个支架均为相同颜色的同种零件，安排少于6个零件时，再安排下一个颜色。每一种零件的总需求量除以6后向上取整，得出来的同种颜色的相同零件排满的滑橇数，然后依次摆放在上一次数组个数的后面，以此类推来将表1里面的所有颜色的零件都摆放在一维数组里面。如果碰见约束条件而不得已将同种颜色不同产品的零件与上一次的数据隔开，则允许向后推移或者放在最后一圈进行调整排放。每完成一个周期后，重新调整需求量并找出所有颜色中能符合约束条件的产品滑橇最大数。

根据颜色分类后按照需求量得降序建立表2：

3.2模型假设

根据题干的信息可以计算出一圈可放置303*6=1818个支架，而根据表1种数据，使用哈密顿有向图模型的方式进行排布方案，即在不考虑切换颜色消耗滑橇作为换色的情况下，将每种颜色的零件除以6向下取整可得2210，即安排满零件支架的滑橇数量，然后将2210除以303向下取整得7圈，将2210mod 303=89，即第8圈还需要占用89个滑橇，将每种颜色的零件数mod 6可得每种颜色的零件剩余数量，接着将同種颜色的同种零件安排在相同的滑块内，接着安排同种颜色的下一种零件，当同一颜色的不同零件安排完了，再切换下一种颜色的零件，如此反复直至全部安排完成，如此可得：

1）假设题干中里面前七个生产周期几乎一致，在第八圈有相应的位置和数量的修改。

2）假设在八个生产周期里面，为了减少人工干预和换色次数而采取八圈均匀分配，即八圈均匀分配后，得到2种情况：

情况一：产品可喷漆量正好分配完;

情况二：产品可喷漆量大于需求量，可以完成需求且生产力有富余。

3.3定义与符号说明

3.4模型搭建

根据数据对每种产品分别求出单圈最大完全利用滑橇数（没有空支架）和所需滑橇数，并进行比较，需求量大者优先原则，最后处理需求量少的产品。若产品所需滑橇数量小于限制数量，则此圈此产品可使用所需求的滑橇数。若所需滑橇数量大于限制数量，则在此圈使用此产品的所有滑橇（没有空支架）。当此圈结束后，下一圈安排相同颜色的量大的异种产品进入喷漆，以此类推即可满足换色次数最少。

将每圈的颜色能够最大利用的滑橇数看作节点f由支架上限作为限制），寻找其他的颜色中零件种类不重复的节点，依次寻找使之构成哈密顿通路。若存在多个换色次数相同且换色次数最少的哈密顿通路，则他们在换色成本的消耗是相同的。

3.5模型求解

伪代码：

求单圈每种颜色能够使用的滑橇数：Use_num（color）：

要使N最小（实际上最小值为k-1），必得Ji=1，i=1，2，...k。说明颜色相同的零件连续加工。

注意：各个圈任务相同，必须按给哈密顿回路排序，这样第一个圈放置k个过渡板。

综合第一步和第二步，要使更换支架的时间最少，8个圈的加工为周期等量加工。

前七圈的滑块数如表3所示（见251页）（前七圈按照周期性，每圈都一样），第八圈进行微部调整。

4结束语

通过哈密顿通路和回路分别求出8圈的排序和第1个圈的排序，由于考虑到支架的时间，要每圈任务相同，这样有的任务要多完成。可能有的任务完成不了，这样最后一圈要调整。可能造成一部分的浪费或者最后一圈有一定多的人工干预来调整。通过哈密顿图模型排列颜色的顺序，再人工排每个颜色的零件顺序（根据约束条件），可以更快求出最优解。