关于卷积在《数字图像处理》课程中的拓展教学研究

王立 杜培明 周芳 王兵

摘要：卷积运算作为图像空间域分析的重要工具，在《数字图像处理》课程的本科教学中占有重要地位。近年来随着深度学习架构的飞速发展，卷积运算成为深度学习技术的重要组成部分，并在图像工程和机器视觉领域得到广泛应用。课程教学中，应与时俱进，探索在图像空间域的传统卷积应用基础上，结合深度学习框架，介绍卷积的各种变体及应用场景，将图像处理课程教学与人工智能机器学习大背景有机融合，使学生更加深入透彻的理解卷积算法并能够在实际场景中应用深度卷积网络，以适应大数据、云计算背景下的新工科教育。

关键词：图像工程;卷积;卷积神经网络;机器学习

中图分类号：TP399 文献标识码：A

文章编号：1009-3044（2020）10-0145-03

《数字图像处理》课程内容与计算机视觉、机器学习和人工智能都有交叉融合的部分，是一门综合性课程，根据研究内容和方法的不同可分为三个层次：图像处理、图像分析和图像理解。而卷积运算作为一种重要的时域处理工具，无论是在像素级的图像处理上（如平滑去噪）还是在抽象层次上的图像分析（如基于边缘提取的图像分割），甚至是最高级别的图像理解上（如特征提取和目标和识别）都发挥着重要作用。

随着大数据和智能计算时代的来临，数据量和计算能力及图像工程的各个领域也发生了质的变化。无论是图像工程的哪个层次都更注重模型的建立和数据的训练计算。传统的《数字图像处理》教学也应结合当前的技术趋势在内容上进行拓展，实现人工智能时代的新工科教育。以卷积运算为例，作为一种基元的特征提取工具和一种特殊的数据压缩工具，在机器学习和深度学习模型的建立上同样发挥着重要的作用，如卷积神经网络（CNN）便是一个典型的代表，无论是在像素级的图像处理还是更高层次的图像分析和图像理解都能够应用并取得很好的效果。因此，在教学中，不应拘泥于传统方法的讲述，更应该结合当下技术的发展，赋予传统方法新的内涵，更加洞悉方法的本质。学生不仅是学习方法，更是拓宽思维。培养学生建立起智能计算时代应该具备的分析解决问题的思维模式。本文主要通过三个部分对卷积运算进行教学拓展：首先是阐述卷积的定义和性质，其次是介绍卷积运算在新的应用中可能出现的变体形式，最后论述了卷积在图像工程中的各种应用，包括传统经典的应用和新技术新框架的应用并得出结论。

1卷积在二维图像处理中的使用

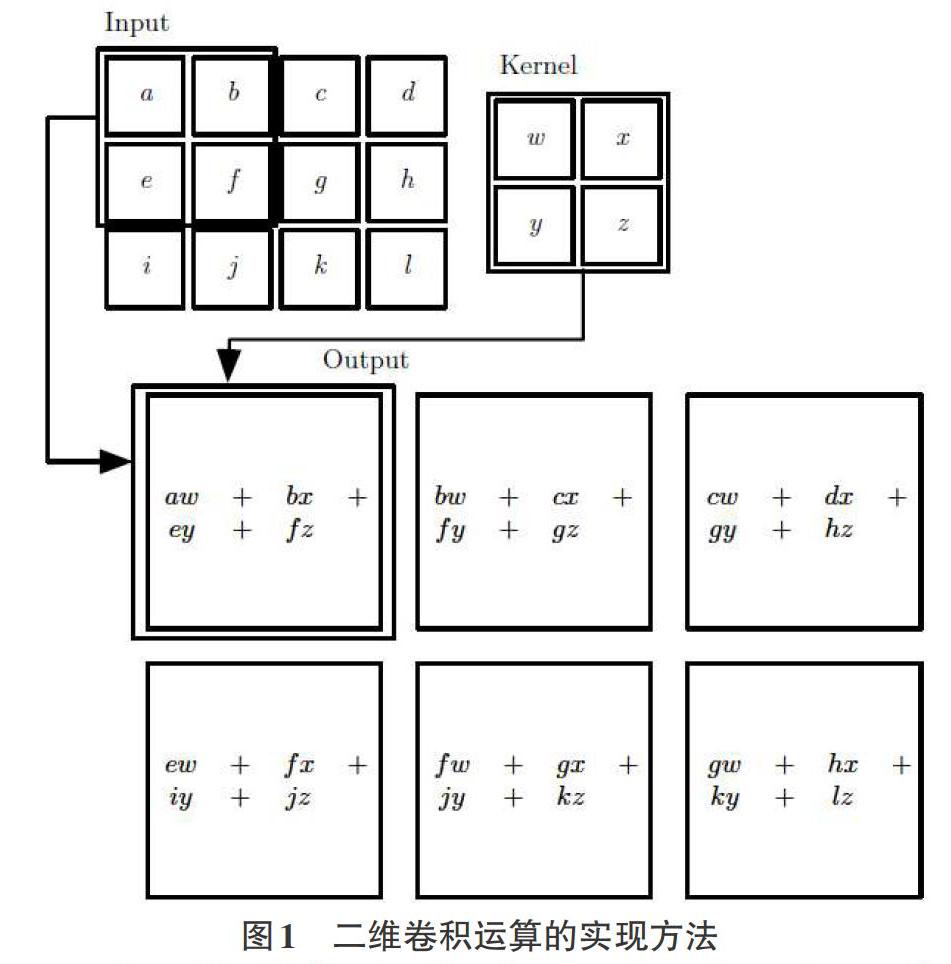
通常来说，卷积运算是具有可交换性的，需要将核相对于输入进行翻转。而互相关函数和卷积运算几乎一样，但是并没有对核进行翻转。许多机器学习的库实现的是一个相关函数但称之为卷积，卷积是核特征的复制查找。因此，在教学中须对这里进行说明，以去除学生在编程应用中疑惑。二维卷积的实现方法如下图所示：

图像与模板的卷积从本质上就是求取图像与某一函数的相似性。举例来说，图像与高斯拉普拉斯函数的卷积就是获取图像与高斯拉普拉斯函数的相似性。当图像中存在区域与高斯拉普拉斯函数的曲线形状相似时，图像的卷积响应达到最大。因此通过各种各样的卷级模板可以捕捉图像中各种特征。

在传统意义上的图像处理课程教学中，关于卷积的概念，通常是在空间域的图像增强部分讲解，它以掩模的形式，作为空间域滤波的基础，与频率域的滤波器相对应，可以进行平滑与锐化的操作。锐化作用在图像分割部分可进一步延伸为边缘提取，作为分割的重要方法。而随着CNN的出现，卷积的内涵进一步拓展，拓展至基础特征提取、拓展至网络模型的连接方式，通过对卷积的延伸讲解，使学生从新的角度认识理解卷积的重要作用，如特征基元的提取和连接方法的优化。首先可以从卷积运算的性质作为切入点并展开拓展，通过应用操作使学生对卷积的本质加深理解。而将卷积加入神经网络之中所形成的卷积神经网络就可以将特征提取和识别集中到一个学习机当中。下面就从卷积的性质和变形应用两方面，让学生理解卷积操作作为连接方式的可能性，将像素级的图像处理与机器学习模型有机地结合起来。

2卷积的性质及其变体

2.1卷积的性质及其应用于机器学习的动机

卷积运算不但能够在空间域对图像进行增强运算，同时还由于它的某些性质成为其能够应用于机器学习的动机，主要体现在：稀疏交互，参数共享和等变表示三个方面。使学生了解到，这些性质使卷积能够应用于神经网络的连接部分，极大改善应用于机器视觉的神经网络的调参和训练。

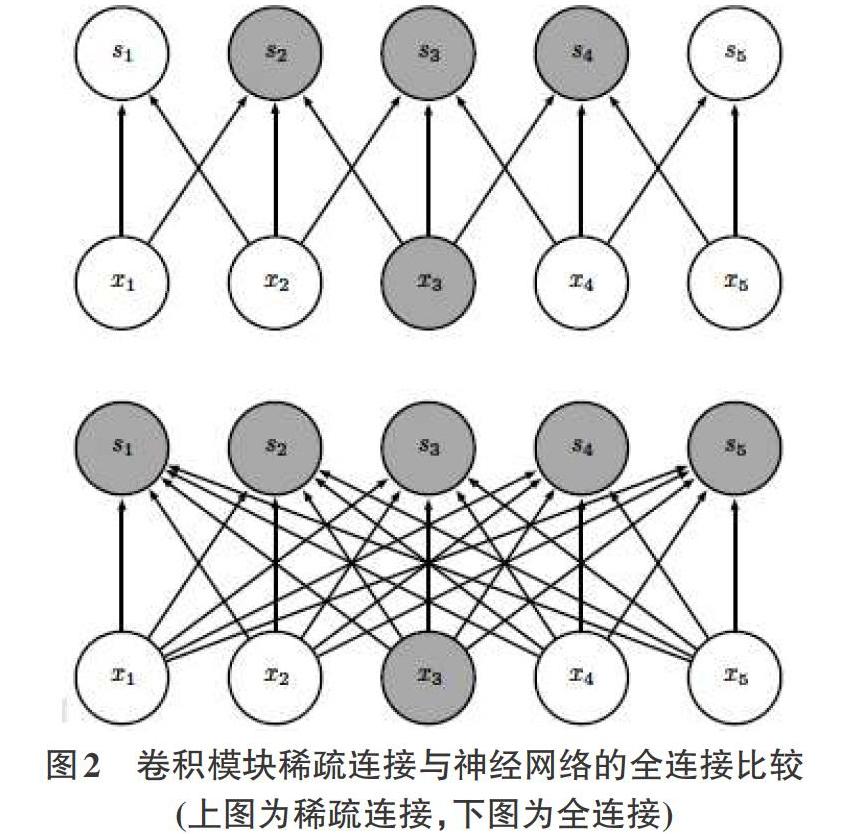
a）权值连接的稀疏交互性质

传统的神经网络是通过使用全连接参数构成的矩阵乘法建立输入与输出的连接关系，即每一层的每个神经元都与相邻层的所有神经元建立连接。而加入卷积模块的网络的连接则相对稀疏，由于通常卷積核的大小远远小于输入的大小，因此当卷积核在图像上滑动遍历时使用的相同的权值，这将大大减少权值的数量。两种连接方式的比较如图2所示。这样不仅减少了模型对参数空间的储存要求，还提高了它们的运算效率。比如有m个输入和n个输出，那么需要调整m×n个参数，相应调参算法的时间复杂度为O（m×n）。而卷积模块的稀疏连接使得输入的数量大幅度减小，从而减少调参计算量，提高计算效率。在课程讲述中，可对比讲解神经网络的普通架构以加强学生的理解。在实际应用中，只要k比n小几个数量级，就能在机器学习中取得好的表现。稀疏交互的图形化解释如图2所示。

b）参数共享性质

参数共享指的是在同一个模型中的多个函数运算中使用相同的参数。在带有卷积层的网络中，由于卷积运算在整个图像上遍历滑动，卷积核的每一个元素都作用在输入的每一个位置上，因此卷积运算中的权值参数是共享的。这种共享保证了整个输入只需要学习一个参数集合，即卷积模板权值，它可以显著地把模型的存储降低至k个参数，并且k通常比m小很多个数量级。由于m和n大小大致相同，而k在实际中相对于m×n是很小的，因此卷积在存储空间和计算效率方面都大幅度的优于单一的密集的矩阵乘法的运算。讲解时可通过程序代码进一步说明。

c）等变表示性质

等变表示有些类似于信号与系统中的线性时不变系统，线性时不变系统的不变指的是输入在时间轴上的移动会带来输出在时间轴上发生相同的移动，而等边表示的不变则是指在空间上输入与输出的等变移动。例如，在用卷积模板来提取图像的局部特性时，如果输入中的特征对象发生移动，卷积运算产生的特征表示也会在输出中移动同样的量。在卷积神经网络的首层通常是卷积层，卷积层包含了各种各样的卷积模板，这些卷积模板得到的各种局部灰度、色彩发生变化的局部特征，而这些局部特征会在图像的各个区域反复出现，不同的局部特征排列组合又构成不同的高阶特征。因此，卷积层的参数共享和等变表示极大地减少计算量，提高模型的调参效率。

卷积运算除了通过稀疏交互、参数共享和等变表示这三个方面的性质来改进机器学习模型的应用外，还提供了一种处理大小可变的输入的方法。这样输入的图像可以不必把分辨率调整到统一模式。因此，在机器学习领域产生了一种重要的网络架构：卷积神经网络（CNN）。这种架构极大地改善了机器视觉中的检测和识别工作，甚至是在图像分割、去噪等图像分析和处理领域也取得了很好的效果。

2.2基本卷积核的变体

在卷积的某些应用场合，特别是在机器学习的网络架构中用的卷积层时，通常不是指那种标准的离散卷积运算，而是对卷积的形式进行某种改变以期达到更好的学习效果。通过介绍空洞卷积和平铺卷积这两种卷积变体在深度模型架构中的应用，使学生对卷积的理解不止停留在基本的掩模运算。

2.2.1空洞卷积或扩张卷积（dilated convolution）

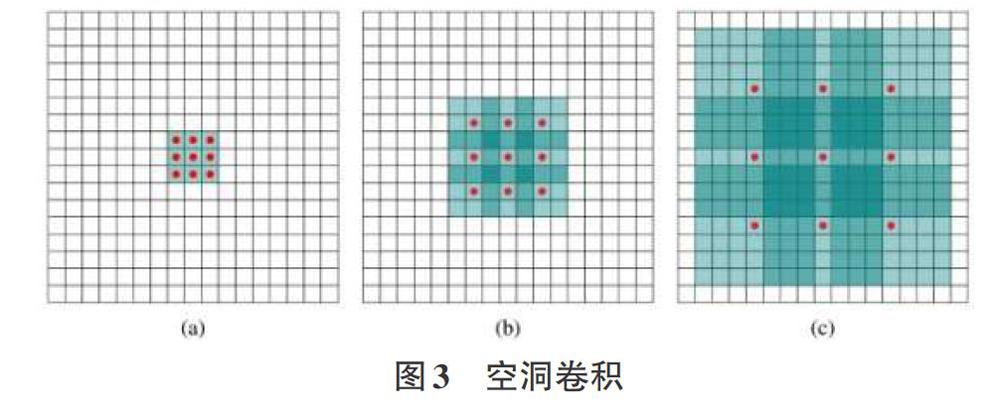
一般的卷积神经网络是通过卷积层和池化层的交替使用来达到特征提取和降维的作用。而空洞卷积（扩张卷积）则是通过在卷积模板中增加空洞，即权值为O的元素来达到感受野面积不变，但可以一步达到需要的降维输出。特别是在FCN，即全连接卷积神经网络中，由于其需要不断通过池化和上采样的反复操作来实现语义分割，用传统的卷积模板会造成特征信息的丢失。如果采用空洞卷积的方式，则可以在感受野面积不变的情况下一步实现特征提取和反卷积的同时，特征信息减少丢失。空洞卷积的示意图如下图3所示：

其中（a）图为3x3的一般卷积模板;（b）图对应（a）图的2倍扩张卷积模板，可以看到对于7x7的区域，只有9个标记为红色的点和卷积核进行卷积操作，其余点权值为0。因此虽然卷积核大小只有3x3，但是这个卷积所覆盖的感受野却达到了7x7;（c）图是4倍空洞卷积操作，同理可推断其能达到15x15的感受野。相比之下，空洞卷积的感受野在权值连接数不变的情况下是呈指数级的增长。因此，空洞卷积的优点是在没有进行池化损失信息的前提下，较大得扩大了感受野，使每个卷积的特征输出都包含了较大范围的信息。

2.2.2平铺卷积

平铺卷积是对卷积层和局部连接层进行了折中，它并不是对每一个空间位置的权重集合进行学习，而是学习一组核使得当对象在空间移动时卷积模板可以循环利用。这意味着在紧邻的位置上拥有不同的过滤器，就像局部连接层一样，但是对于这些参数的存储需求仅仅会增长常数倍，这个常数就是核的集合大小，而不是整个输出的特征映射大小。具体的卷积运算方式如图4所示：

假设平铺卷积有t个不同的核，上图表现的是t=2的情况。其中一个核具有标记为“a”和“b”的边，而另一个具有标记为“c”和“d”的边。如果输出右移一个像素，则使用一个不同的核，即输出中的相邻单元具有不同的参数，在遍历所有可用的t个核之后，循环回到第一个核。如果两个输出单元间隔t个步长的倍数，则它们共享参数。由于权值的近处无关，远处相关，平铺卷积可以学习到更加复杂的不变性。

3卷积的应用

3.1卷积核在传统的图像增强领域的应用：

卷积运算在传统图像处理领域主要应用在图像增强f如平滑，锐化）和边缘提取等方面。卷积核通过局部的简单差分运算实现图像空间域上的微分运算，如一阶、二阶微分算子，通过这些微分算子的卷积运算实现噪声的平滑和边缘的提取。常用的算子有一阶的Prewitt算子，Sobel算子等是通过对中心像素的系数加权形成不同的卷积模板;Carmy算子则是在一阶算子的基础之上，增加了非最大值抑制和双阈值两项改进提高了检测的精确度;二阶算子，如LOG算子，Laplacian算子等，可进行更加细致的边缘检测;卷积窗口就是一个滤波模板，通过微小窗口的代数加权运算实现对图像局部特征的提取抽象，所谓特征提取即是对图像特征的抽象表示，是对图像数据的抽象压缩。卷积模板是在二维空间中的数据抽象，高阶的特征抽象是由低阶的局部细小特征进一步抽象所得到的，因此卷积模板作为局部特征的提取基本运算有着十分重要的作用。

3.2卷積运算在深度卷积网络中的应用：

传统的图像特征提取方法，如边缘检测、SIFT、SURF、Haar特征等都是基于图像局部的一阶二阶微分计算得来。伴随着计算能力的大幅度提升，在深度学习技术快速发展的当下，把卷积模板应用到神经网络学习机当中，如卷积神经网络（CNN），可以统一有效地将特征提取的过程用卷积层和池化层来实现。CNN实质上是将SIFT算子等方法全方位融合到一个模型之中，并扩大了规模和细节。而卷积网络由于卷积的稀疏交互，参数共享和等变表示这三个方面的优势得到了巨大的发展和广泛的应用。通过介绍CNN的基本结构对之前讲解的卷积性质可以更加充分的理解。

卷积网络在本质上是一种输入到输出的非线性函数映射，它是一种数据驱动的模型训练，只要用已知的模式和大量的样本数据对卷积网络加以训练，网络就具有输入输出对之间的函数映射能力。通过对卷积神经网络的介绍，让学生理解卷积不但可以作为空间域的二维掩模运算工具，还可以作为高效的权值连接模块来实现数据的抽象和压缩。通过对基本结构示意图的讲解，启发学生，卷积模板提取局部特征的本质并没有改变，每一个卷积层实质上都是一次抽象特征的提取，随着层数的增加，抽象的程度也逐步提升，输入数据的压缩为全连接层的训练提供便利。

卷积神经网络CNN主要用来识别二维图像。CNN的卷积层是通过数以百计的卷积模板构成，这些卷积模板的权值并不是通过人工设计的，而是通过大量的样本数据训练产生，这样就避免了人为的主观局限性;同时，卷积网络由于它的参数共享、稀疏连接等特殊性质，可以在模型的训练中进行并行学习，GPU等硬件的发展使得这种并行学习在硬件层面上得到了解决方案，训练运算效率大幅提升。

卷积神经网络模型的连接结构更接近于实际的生物神经网络，并且权值共享降低了网络的复杂性，具有高维输入向量的图像可以直接输入网络，一次性解决特征提取，特征选择和特征分类这些步骤，避免了人工设计特征提取方法和分类过程中人的主观判断和多个模型计算的复杂度。成为计算机视觉中的各种模型和解决方案的基石。

目前，卷积神经网络已经广泛应用于机器视觉，图像目标检测识别，语音识别等方面并取得了巨大的发展，日臻成熟完善。随着GPU等并行计算的硬件广泛应用，卷积网络的深度也进一步提高，应用效果不断提高。当然，卷积网络也由于其模型参数巨大（数以万计）而在训练中存在诸多瓶颈，模型对噪声的敏感度较高，对方向及位置关系的表述能力较差，这些缺点还有待研究改善。但是无论模型怎样改进，卷积层作为基元特征提取的主要部分是要予以保留的。

在深度卷积网络的应用中，还可以进一步通过卷积运算的变体来改进卷积网络，使其应用的环境更加广泛。如使用全连接卷积网络（FCN）可以实现基于像素的语义分割，结合前面所述的卷积变体，将全连接卷积网络的卷积部分改进为空洞卷积则能够实现半监督或弱监督的图像语义分割，减少由于图像像素级标注带来的困难和麻烦。将这些改进的卷积网络应用于图像分割的效果如图5所示，这些模型更适合复杂场景的分割，分割的结果也更符合人类认知。而平铺卷积作为局部连接和传统卷积的折中改进，能够改善深层卷积网络的训练速度和训练效果。因此学生可以体会到卷积运算及其变体正在以前所未有的速度广泛应用于人工智能和机器学习技术的方方面面。课程教学中可适当应用深度学习框架演示上述算法的应用（如YOLO、SSD等），展示其强大的功能。

4结论

本文通过论述在《数字图像处理》本科教学中卷积运算的讲解内容拓展，表明在智能学习的大背景下，传统的运算方法有着新的内涵和应用。从基本概念的讲述到其变体在图像工程中的应用演示，使学生理解卷积运算不但能够进行边缘提取、图像平滑、锐化等基本操作，还可以应用于深度卷积网络，完成目标检测分割等图像工程的高级阶段。在教学中，应拓展传统方法的讲解，结合当下技术发展的前沿领域，综合论述传统方法所赋予的新含义和新应用，并结合具体的应用场景对这些方法和模型进行演示，举例说明。使学生对一些经典方法有更深更透彻的理解，能够对一些基本深度卷積模型进行应用。学生通过课程的学习对机器学习和人工智能行业也有了一定的了解和认识，能够更好地体现新工科时代的专业教育。