基于改进响应面的刚构-连续梁桥有限元模型修正
2020-06-08张梓乔雷建平
张梓乔, 雷建平
(武汉理工大学 交通学院,湖北 武汉 430063)
0 引 言
近十年来,响应面法在模型修正方面的应用价值不断提高,对比传统有限元模型修正方法,响应面法以显示函数形式表达了输入变量与响应的关系,无需重复调用有限元模型,极大的提高了计算效率,同时基于统计分析指标进行从全局进行显著性参数筛选,较灵敏度法仅根据某设计点的响应变化量来判断参数的影响性更为科学。目前有部分学者基于拟合残差对响应面进行改进[1],但不同响应面残差大小及数量级会有所不同,部分样本点虽然拟合残差较大,响应面的拟合却也已经足够。为判断样本点中是否存在响应面拟合不足的异常点,并增强响应面在该点局部的拟合能力,本文基于内学生化残差值寻找失拟样本点,并在该点引入高斯径向基函数重新构造响应面,结果表明,改进后响应面对所有样本点拟合均良好,基于改进响应面修正后的模型满足实际工程要求。
1 基于响应面的结构有限元模型修正理论
基于响应面的有限元模型修正基本原理:选取适当的因变量,在合理的结构参数范围内,通过试验设计方法选取有代表性的样本,通过有限元软件计算得到对应的结构响应数值;通过方差分析等方法,筛选与响应值显著相关的参数;选取合适的响应面函数,对样本进行响应面拟合并进行检验;以实测数据构造目标函数,用响应面模型替代原有数值模型进行参数优化,得到修正后的参数,最终代回有限元模型得到修正后模型。
1.1 试验设计
常用的试验设计方法有正交设计(OA)、最优设计(Opt)、均匀设计(UD)、中心复合设计(CCD)及Box-Behnken设计(BBD)。在拟合二阶响应面时,CCD由于其良好的正交性及可旋转性,应用最为广泛。CCD在2k全因子设计的基础上,增加2k个坐标轴点和n个中心点(有限元计算为确定性试验,n取1),对于k个变量的设计共需要2k+2k+1个样本点,当待修正参数过多时,该试验方法工作量较大,不适合多参数的试验设计。文中所采用的试验设计方法为D-最优设计(Opt-D),其回归模型表达式如下:
ya=β1f1(xa)+β2f2(xa)+…
+βmfm(xa)+εa,a∈(1,2,…,N)
(1)
式中:εa是服从N(0,σ2)的相互独立的随机变量;xa是设计空间内的样本点;f1(xa),f2(xa),…,fm(xa)是设计空间内的连续函数;β1,β2,…βm为待估计参数,其值通常由β1,β2,…βm表示的密集椭球体体积最小值确定。从数理统计方面来看,Opt-D的目标为使响应面函数的设计参数样本估计方差最小。该法是仅考虑方差而得出的一种准则,忽略了偏差的影响,但当参数限制在关注区域内时,该准则会显出很大的优越性[2]。
1.2 参数显著性检验
在数理统计中,方差分析是研究自变量是否对因变量有显著性影响的一个重要工具,常用的有F检验法[3],其过程总结如下:首先计算出样本数据中由试验因素引起的偏差平方和SSE和由各个因素引起的偏差平方和SSA,然后分别除以各自的自由度得到均方残差(mean-square error,MSE)及均方回归(mean-square regression,MSR),最终求出F值,其计算公式如下:
(2)
式中:fA为因素的自由度;fE为试验偏差的自由度。
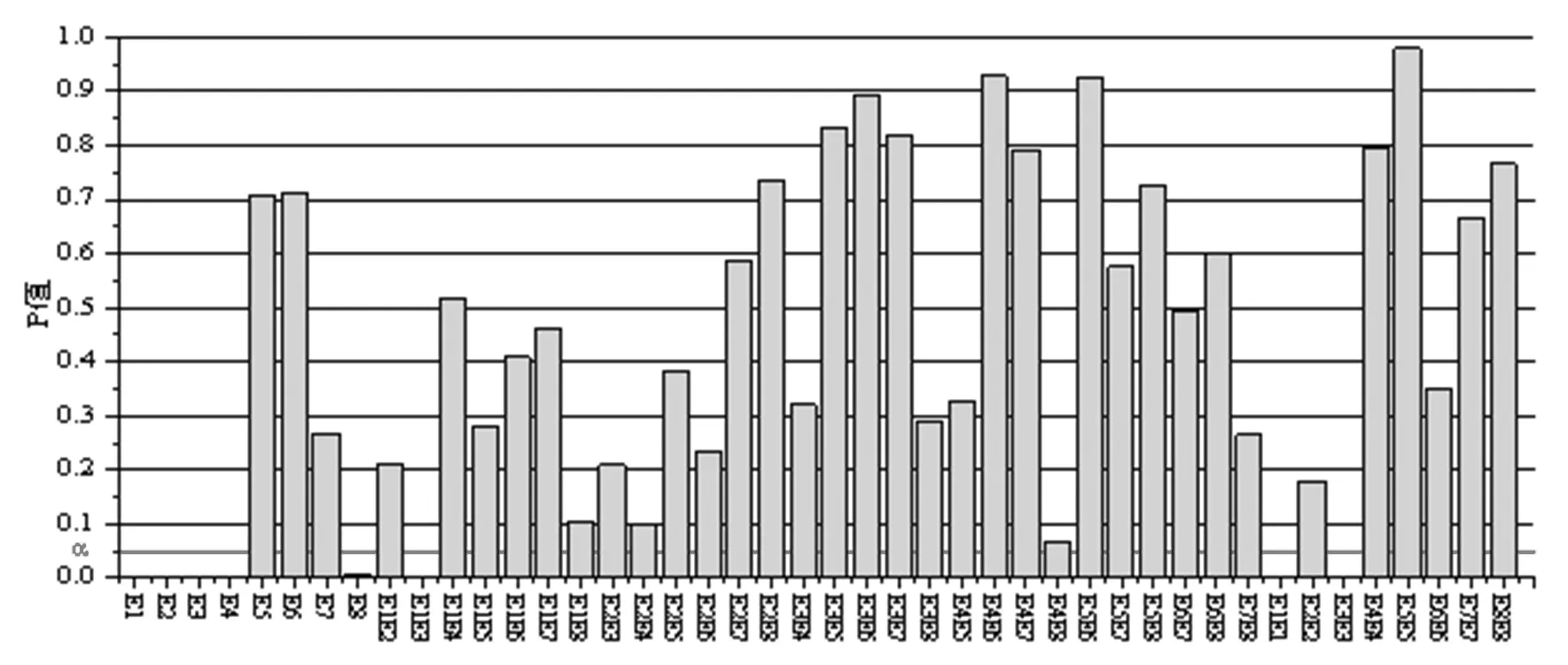
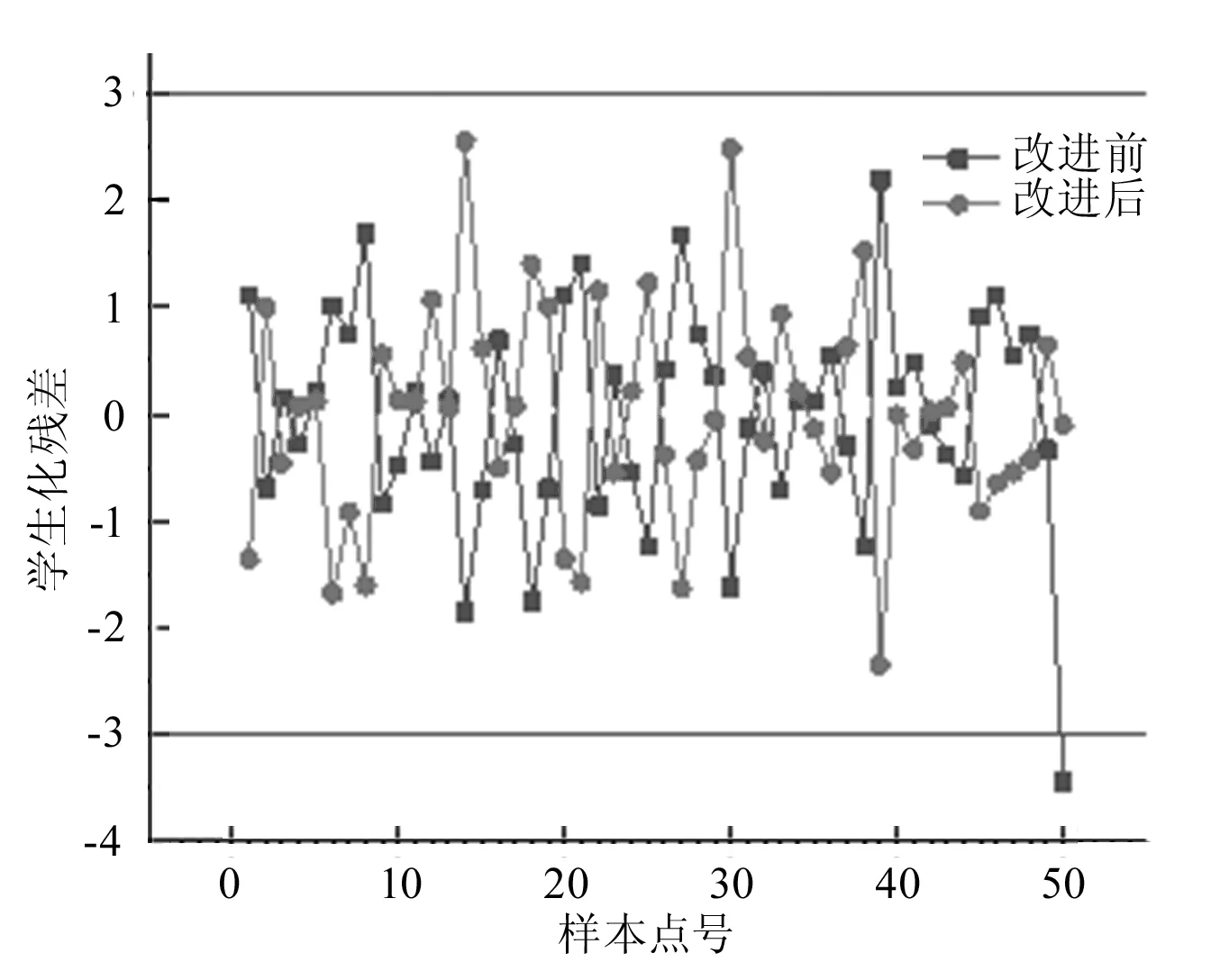
在求出待检验参数的F值后,与临界值Fα进行比较,其中α为置信区间,表示判断错误的概率,常用的判断标准为:当F≤0.01,则因素影响高度显著;0.01 常用的响应面拟合函数有以下几种:多项式函数、径向基函数、多元自适应回归样条、克里格(Kriging)模型。本文响应面以完备二次多项式为基础,在异常点处引入高斯径向基函数改进局部非线性能力。 完备二次多项式响应面函数表达式如下所示: (3) 式中:xi、xj为待修正参数;k为待修正参数总数;β0、βi、βii、βij为各项待定系数。 径向基函数通常定义为空间中的任意一点到某个中心之间的单调函数,其结构灵活、形式简洁,对解决非线性问题有独特的优势,高斯径向基函数形式为[4]: (4) 响应面拟合后需对其精度进行检验,常用的响应面精度检验指标如下[5]: (5) (6) 复相关系数R2和相对均方误差RMSE均属于[0,1],且R2越接近1,拟合精度越高,RMSE越接近0,拟合误差越小。统计学中通常采用内学生化残差值来判断拟合异常点,其计算公式如下: (7) 式中:s为标准误差,hii为帽子矩阵H主对角线元素。若某一点SRSEIDi超出[-3,3]区间时,可以97%置信度判定为异常点。 有限元模型多目标参数优化问题可用如下数学形式表达[6]: minF(x)=min(f1(x),f2(x),…,fn(x)) s.t.gi(x)≤0,i=1,2,…,m (8) 式中:fi(x)为各变量初始目标函数;F(x)为转换后的多目标函数;gi(x)为约束函数。 神定河大桥为66 m+3×120 m+66 m预应力混凝土变截面刚构-连续梁桥,单箱单室截面,桥面宽度为15m。下部结构连续梁处采用桩柱式墩,刚构部分采用双薄壁墩,桥面铺装采用普通沥青混凝土。设计荷载为公路-Ⅰ级,人群荷载为为2.65 kN/m3。箱梁采用C55混凝土,双薄壁墩采用C40混凝土,质量密度均按2 600 kg/m3计。箱梁、桥墩均采用实体单元建立,桥面铺装部分仅考虑其附加质量,不考虑刚度贡献[7],薄壁墩底部约束全部自由度,墩顶与箱梁固接,箱梁各处支座根据支座形式对相应节点施加竖向、横向、纵向约束。 以静载各工况挠度作为响应特征值,以各区段弹性模量作为待修正参数,取0.8倍初值作为低值、1.3倍初值作为高值,采用D-最优设计法进行试验设计,代入有限元模型进行计算,A、C、E截面各3个测点,共得到50个样本点。弹性模量分区示意图如1所示。 图1 参数修正区间分段图 采用F检验法分析各待修正参数对静力响应的显著性影响,计算各待修正参数对各静力响应的显著性水平P值。为节省篇幅,后续仅列给出静力响应面Y1的表达式及相关图表,如图2所示。 图2 Y1参数显著性检验图 有图2可知,Y1静力响应面共有8个待修正参数,利用Design-Expert软件将所有样本点数据拟合原始二次响应面,函数形式如下式所示,拟合后内学生化残差图如图3所示。 图3 Y1样本点内学生化残差图 Y1=-21.65311+3.08379E1+0.025070E2 +2.70203E3+0.027664E4+0.012308E8 -0.095298E1E3-0.22618E1E1-0.19576E3E3 (9) 由图3可知,第50号样本点内学生化残差值超限,这表明二次响应面对该点的拟合能力存在缺陷,为改进该点局部非线性能力,引入高斯径向基函数,利用MATLAB对各待定系数进行重新求解,最终静力响应面Y1函数表达式如下式所示,改进前后内学生化残差比较图如图4所示。 图4 Y1响应面改进前后内学生化残差比较图 Y1′=-21.758 3+3.082 7E1+0.027 2E2+ 2.748 2E3+0.029 9E4+0.014 1E8- 0.094 5E1E3-0.226 2E1E1 -0.202 2E3E3- 0.048 7e-[(E1-4.615)2+(E2-4.615)2+(E3-4.091)2+(E4-4.615)2+(E8-4.225)2] (10) 由图4可知,改进后响应面内学生化残差值均落入[-3,3]区间内,对所有样本点拟合均良好。Y1~Y3响应面改进前后检验指标见表1。 表1 Y1~Y3响应面改进前后检验指标比较表 采用响应面模型替代有限元模型,基于静力响应实测值构造目标函数,运用改进双链量子遗传算法对待修正参数进行优化求解,各区段弹性模量修正后值较初值都有一定增大,修正幅度最大为12.59%,较为符合工程实际,分析认为是预应力结构中配置了大量的预应力钢筋及普通钢筋,结构整体刚度有较大的增强。 将修正后的参数代回有限元模型重新计算各工况静力响应,静力响应最大误差由12.32%降至3.67%,有限元计算值与实测值吻合较好。笔者用修正后的模型重新计算竖向前三阶频率,发现在区段7弹性模量(区段7的弹性模量对A、C、E的9个挠度测点基本无影响)及各区段质量密度均未修正的情况下,频率最大误差由9.12%降至3.99%,修正效果也较为理想,后期以修正后的弹性模量建立动力响应面修正区段7的弹性模量及各区段质量密度后,发现质量密度变化较小,修正后频率最大误差降至1.15%,动力修正后的频率误差整体较挠度误差小,分析认为频率测量误差较挠度测量误差小。 基于动静力实测数值,采用改进响应面法对一座五跨刚构-连续梁桥进行了有限元模型修正,通过在异常点处引入高斯径向基插值函数,有效地改善了局部的非线性拟合能力,以实测数据构造目标函数并进行参数优化,修正后的结果与实测值吻合较为良好,修正后的有限元模型对结构的损伤识别及状况评估具有一定的意义。 完备二次响应面拟合精度已经较高,但最适宜二次响应面建立的中心复合设计应用于多参数试验设计时,工作量十分巨大,若能在不严重影响其正交性及可旋转性的基础上适当减少样本点,试验设计的层次性及响应面的准确度能得到进一步改善。1.3 响应面拟合
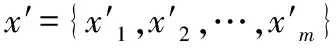
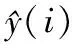
1.4 参数优化
2 神定河大桥有限元模型修正
2.1 神定河大桥初始有限元模型
2.2 响应面模型建立



2.3 参数修正
3 结 论
