双基地合成孔径声呐时间同步误差分析

郭 慧 黄 勇 王迎迎 刘纪元

(1 中国科学院大学 北京 100049)

(2 中国科学院声学研究所 北京 100190)

(3 中国科学院先进水下信息技术重点实验室 北京 100190)

0 引言

双基地合成孔径声呐(Bistatic synthetic aperture sonar，Bi-SAS)是一种收发分置的新型声呐体制，与常规成像声呐相比，双基地成像声呐具有显著优势：收发分置，灵活性好；探测效率高；充分利用目标的散射特性；探测安全性高等[1]。同步技术是双基地成像声呐系统的核心技术之一，包括时间同步、相位同步和运动补偿，分别指收发换能器具有统一的时间标准、相位对齐以及对运动轨迹偏移的补偿，其中时间同步是需要解决的一个重要问题。

国外对双基地声呐的理论与应用的研究比较多。20世纪90年代起，双/多基地声呐系统研究进入新阶段，主要成果有目标散射特性、海底混响、目标探测等理论方面的研究，并研制出了部分实验样机。如1998年由MIT 和SACLANTCEN 联合的GOATS 项目，致力于研制适用于沿海环境的反水雷系统，实现了对掩埋物的探测成像，但该系统中未考虑时间同步误差的补偿，成像效果不理想[2]。

我国对双/多基地声呐研究起步较晚，主要集中在目标散射特性、定位原理及成像算法等理论方面的研究[3-6]，对时间同步技术的研究不多，尚无有效的时间同步系统。雷达系统中常用的同步技术有基于GPS 和运动传感器同步[7]、高精度晶振同步、独立式同步法等。但GPS在水下使用范围受限，高精度晶振价格昂贵，这些方法不适用于双基地声呐系统，利用回波数据的声学方法是目前行之有效的一种时间同步方案。

目前Bi-SAS 系统中没有成熟应用的时间同步方案，有必要进行深入的研究[8-9]。文献[10] 指出，双基地声呐系统对时间同步精度的要求是信号压缩后脉宽的若干分之一，即10-3量级，但合成孔径声呐(Synthetic aperture sonar，SAS)无需精确测距，主要关注对回波调频特性的影响，所以本文将对时间同步误差重点进行理论分析。首先给出Bi-SAS几何模型、回波信号模型及时间同步误差模型，计算误差影响下的距离和方位向分辨率，然后理论分析误差对成像性能的影响，最后进行仿真验证。

1 BiSAS回波信号模型

1.1 Bi-SAS回波信号模型

双基地合成孔径声呐三维几何模型如图1所示，假定收发平台做同向匀速直线运动，均以侧视方式工作，并以一定的脉冲重复频率发射和接收声信号。

图1 Bi-SAS 三维几何模型Fig.1 Three-dimensional model of Bi-SAS

从图1给出的几何关系可以得到Bi-SAS 的合成孔径关系。在t= 0 时刻，Bi-SAS 收发平台分别处在某一合成孔径中心位置，RT0、RR0分别为0 时刻发射平台和接收平台到点目标的距离，R0=RT0+RR0为0 时刻收发位置到目标位置的距离和。设t时刻发射平台和接收平台到点目标的距离分别为RT(t)、RR(t)，则t时刻回波信号所经历的距离可表示为

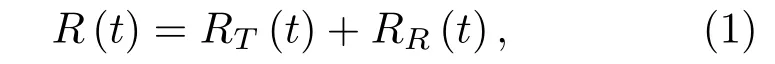
式(1)中，

其中，xT、xR分别表示t时刻发射平台和接收平台相对于初始时刻移动的距离，其值分别为

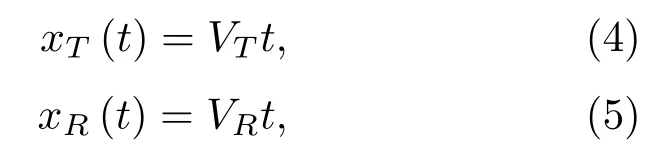
其中，VT、VR分别为发射平台和接收平台匀速直线运动的速度。假设|xT| ≪RT和|xR| ≪RR，根据菲涅尔公式，式(2)和式(3)可以分别近似为

将式(6)和式(7)代入式(1)，可得到

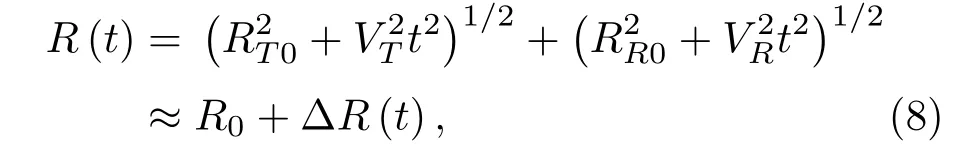
式(8)中，

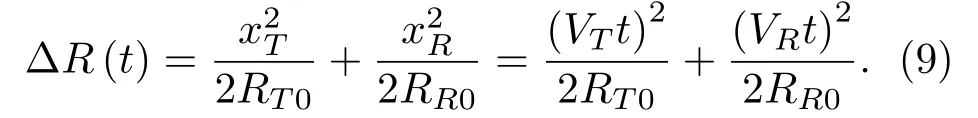
双基地SAS 通过脉冲压缩提高分辨率，假设发射信号是线性调频信号，

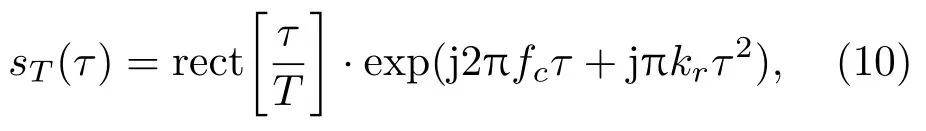
式(10)中，τ为距离向时间；rect(·)为矩形窗函数；T为脉冲持续时间；fc为信号载频中心频率；Kr为线性调频率，其表达式为Kr=B/T；B为信号带宽。

接收回波为延迟后的线性调频信号形式，

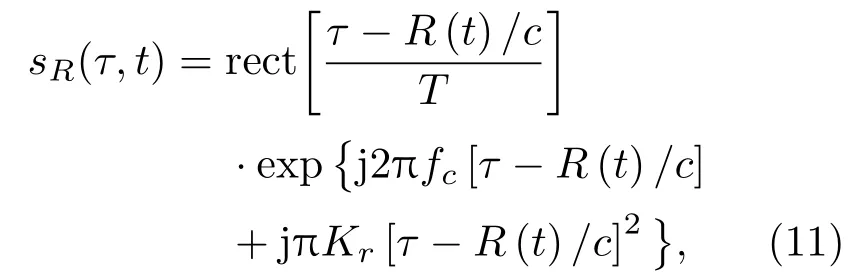
式(11)中，回波信号延迟表示为τd(t)=R(t)/c，t为方位向时间，c为声波传播速度。

接收换能器接收信号本振角频率为2πfc，本振信号为exp(-j2πfcτ)。但实际上双基地SAS 系统发射与接收存在不可忽略的时间同步误差，设接收时间与发射时间相差Δτ，则接收换能器参考时钟为τ′=τ+Δτ，接收换能器本振信号为exp[-j2πfcτ′]。解调后的回波信号为

忽略包络影响，对回波信号式(12)进行距离向傅里叶变换，可得到[11]

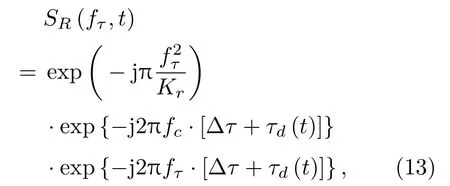
式(13)中，fτ为距离向频率。设频域匹配滤波器为

距离向压缩得到

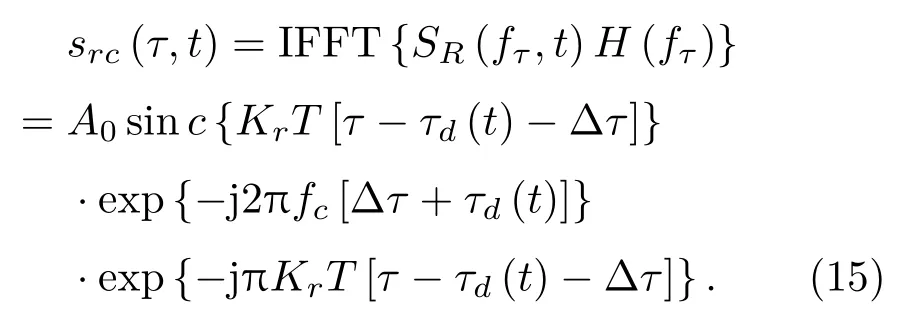
1.2 Bi-SAS的分辨率

收发分置SAS 致使距离向和方位向物理意义明显区别于单基地SAS。收发传播路径不一样使得地面分辨率表示不一致，方位向分辨率也不再是常数。

对于线阵，分辨率一般指波束信号半功率点对应的波束宽度，即常用幅度的-3 dB带宽表示，有

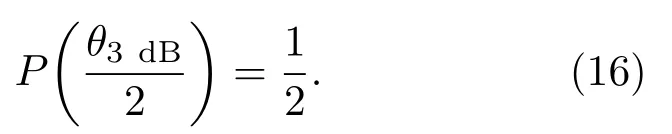
在λ ≪D条件下，角分辨率近似解为[12]

线分辨率近似解为

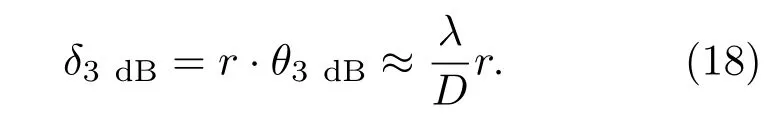
其中，P为信号功率，D为接收阵长度，λ为信号波长。

当同步误差与时间有关时，式(12)表明一次线性误差会对调频率产生影响。设Δτs=β·t+χ，代入式(15)的幅度项得到

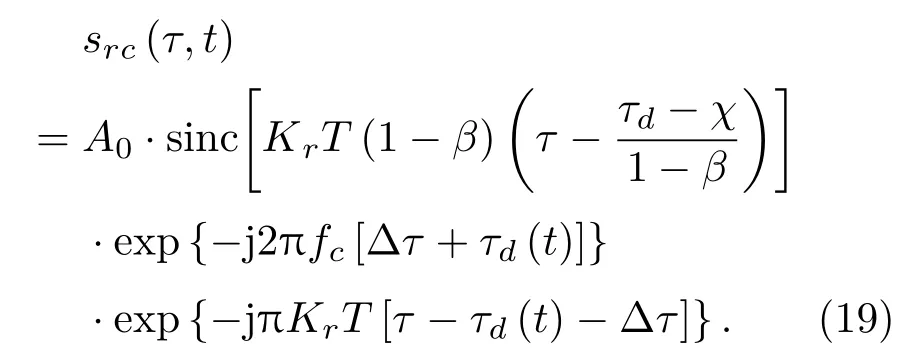
信号经过脉冲压缩后，按其半功率带宽计算分辨率，得到Bi-SAS的时间分辨率为

因此，无误差影响时，Bi-SAS距离向脉压分辨率为

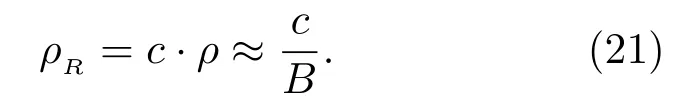
考虑线性时间误差时，Bi-SAS时间分辨率为

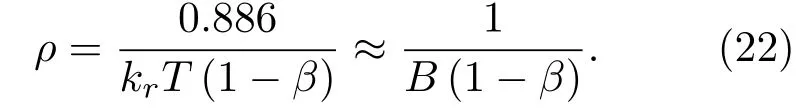
Bi-SAS脉压分辨率为

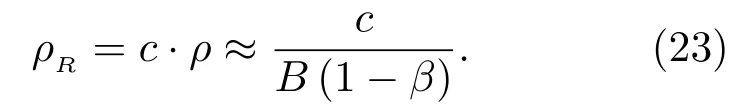
由于双基地声呐配置形式多样，地面距离分辨率随着配置形式的不同而具有空变性。

考虑方位向分辨率，回波信号多普勒频率为

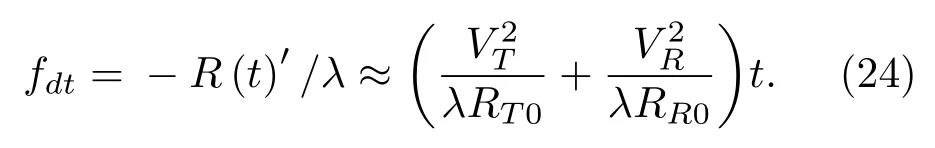
令kV=VT/VR(VR0)，kR=RT0/RR0，对应的多普勒线性调频率为

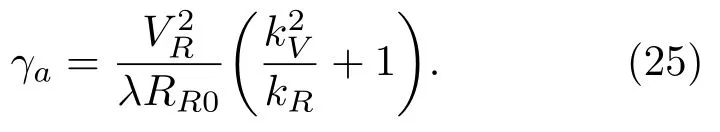
多普勒带宽为

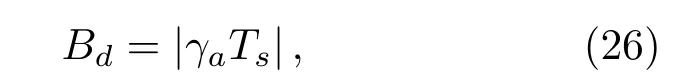
式(26)中，Ts为Bi-SAS 的孔径合成时间，由接收平台参数可以得到

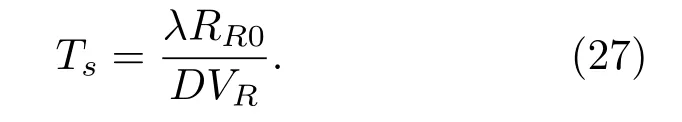
将式(15)中时间表示为时变距离，有

其中，k= 2π/λ表示波数，当ΔR(t)＜ρR/2 时，可以忽略合成孔径长度内斜距变化量对回波延迟时间的影响。将式(28)中时变距离R(t)引起的相位项用方位向多普勒调频率表示，得到

式(29)表明，二次线性误差对调频率会产生影响，设Δτ=α·t2+β·t+χ。设参考信号为

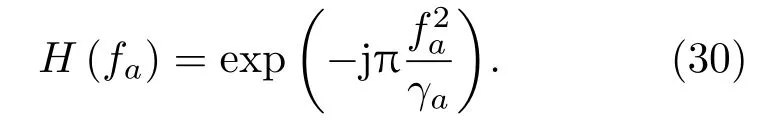
方位向脉冲压缩得到影响调频率的幅度项为

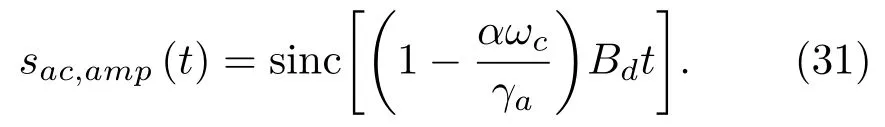
因此，无误差影响时，Bi-SAS的方位向分辨率为

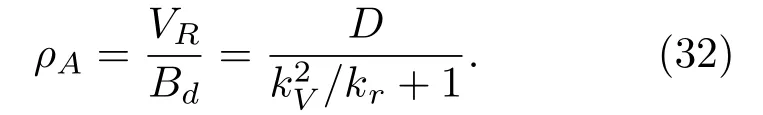
考虑时间同步误差时，方位向分辨率为

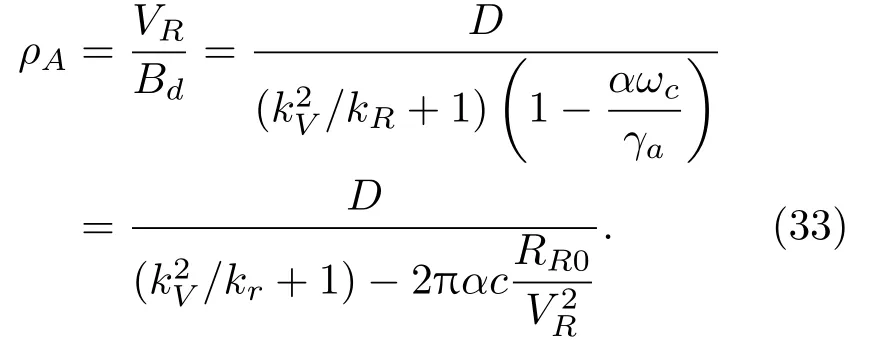
2 时间同步误差分析

2.1 时间同步误差模型

在双基地SAS 系统中，收发换能器的触发脉冲由各自载体平台上的频率源分频得到，时间同步误差主要是发射与接收平台的时钟源不一致与不稳定导致的。将时间同步误差分为3 个部分[13]：收发平台初始触发信号间的时间差Δτ0，收发脉冲重复间隔之差引起的线性时间误差Δτ(t)，以及频率源稳定性引起的随机误差Δτrand。因此，系统的时间同步误差模型可表示为

其中，Δτs(t)为时间同步总误差；第一项为固定时间差；第二项为随时间变化的线性积累误差，假设服从二次线性分布，表示为Δτl=a·t2+b·t；第三项为随机时间误差，服从均值为零的正态分布[14-15]。

基于此误差模型的触发信号时序图如图2所示。

图2 Bi-SAS 收发触发信号时序示意图Fig.2 Transceiver trigger signal timing diagram of Bi-SAS

2.2 时间同步误差影响分析

首先分析收发换能器间只存在脉冲重复频率(Pulse repetition frequency，PRF)触发不同步对成像性能的影响。此时时间误差为固定值Δτ0，将Δτs(t)= Δτ0代入式(13)距离向傅里叶变换表达式，可得到

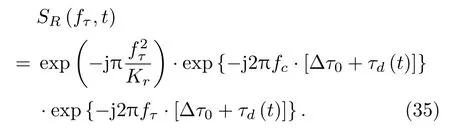
由式(35)可知，固定时间误差Δτ0引入两项相位误差，在距离向引入误差相位项exp(-j2πfτ·Δτ0)，使成像聚焦位置在距离向产生固定偏移，引起回波采样窗的偏移[10]。代入式(23)得到距离向分辨率δR=c/B，由此可见，固定时间误差对距离向分辨率没有影响。方位向引入误差相位项exp(-j2πfc·Δτ0)，不随方位时间变化而变化，因此对方位向分辨率没有影响。

回波采样窗偏移如图3所示，图中Δτ为收发间固定时间差，Be为回波信号有效带宽，T为回波信号时长。当偏移造成回波窗不能完全采样时，会使回波采样信号发生位移、截断，带宽变窄[16]。

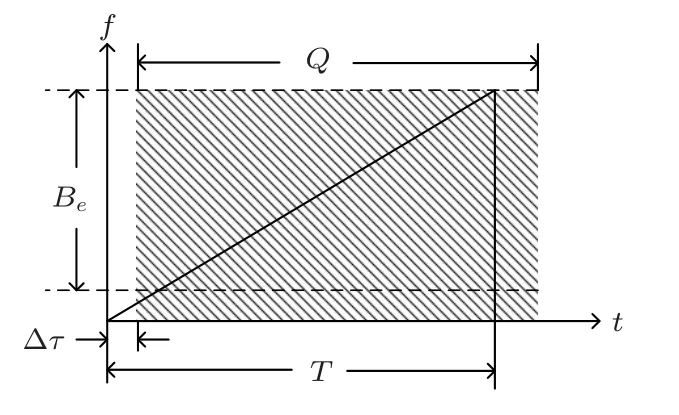
图3 回波采样窗偏移示意图Fig.3 Echo sampling window offset diagram

收发换能器间脉冲重复时间差引起线性时间误差Δτ(t)=a·t2+b·t，线性误差具有累积性，示意图如图4所示。

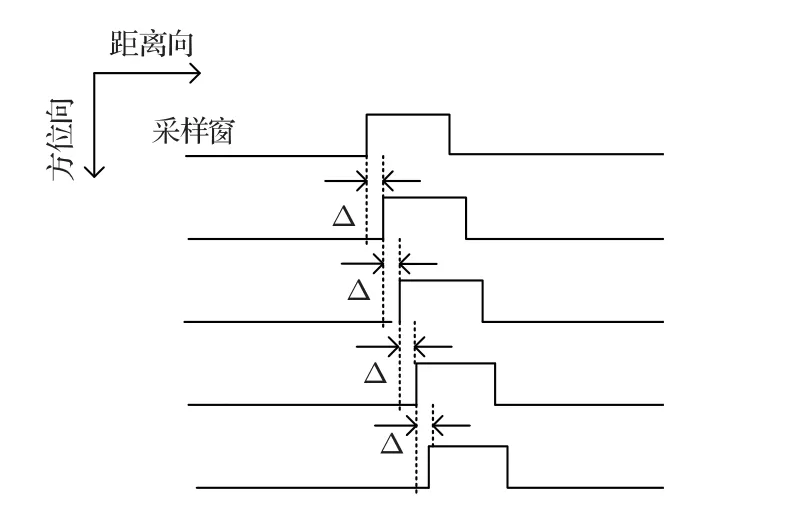
图4 线性时间误差示意图Fig.4 Linear time error diagram

只考虑线性时间误差影响时，将Δτ(t)=at2+bt代入式(13)距离向傅里叶变换式，得到

分析式(36)可知，线性时间误差在距离向引入线性误差相位项exp[-j2πfτ·(a·t2+b·t)]，成像时引起距离向聚焦位置偏移，且偏移量与时间t有关。将线性误差代入式(23)，可得到距离向分辨率为ρR=c/B(1-b)，造成距离向分辨率降低，成像性能下降。

在方位向引入误差相位项exp[-j2πfc·(a·t2+b·t)]，引起复杂的聚焦恶化和方位聚焦位置偏移。代入式(33)，得到方位向分辨率为，造成方位向分辨率降低，成像产生聚焦模糊以及主瓣展宽、旁瓣升高。

随机时间误差是由发射与接收换能器频率源不稳定造成的，累积造成PRF 随时间随机变化，示意图如图5所示。

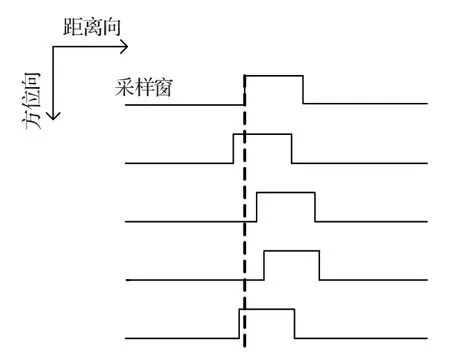
图5 PRF 随时间随机变化的示意图Fig.5 PRF jitter diagram

设发射与接收PRF 随机变化分别服从Δτs(τ)～(0，σs2)与Δτr(τ)～(0，σr2)的高斯分布，则接收端相邻采样窗PRF 随机误差Δτrand也服从高斯分布，此误差在方位向没有累积性。

该误差影响回波信号在距离向和方位向上的调频特性，当时钟源稳定性差或误差较大时，采样所得信号将无法对齐，造成图像旁瓣升高，对积分旁瓣比影响较大。随机时间误差影响的点目标示意图如图6所示。

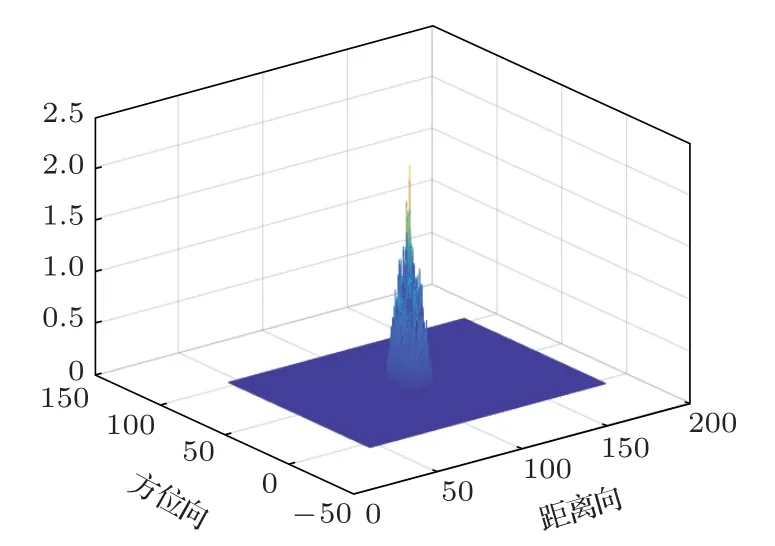
图6 随机误差影响的点目标示意图Fig.6 Point target affected by random error

3 仿真结果

通过对时间同步误差的仿真，以验证对Bi-SAS成像的影响效果，仿真参数如表1所示。

利用表1中仿真参数对3 个点目标进行距离-多普勒(Range Doppler，RD)算法成像仿真，分别加入不同的固定时间同步误差，Δτ0=0、Δτ0=1 ms和Δτ0=10 ms，得到的成像仿真结果如图7所示。

图7 固定时间误差对成像性能的影响Fig.7 Image affected by fixed time error

从图7仿真结果可知，当固定时间误差较小、系统采样窗满足对偏移后信号的完全采样时，仅在距离向引起相应的偏移，对成像质量没有明显影响。但当误差较大、采样窗不能完全采样时，回波采样信号带宽变窄，造成距离向频谱宽度缩短，在成像范围内出现干扰点，明显影响成像性能。

利用表1中仿真参数对一个点目标进行RD 算法成像仿真，加入α= 0.1、β= 0.1 的线性时间误差，得到的成像仿真结果如图8所示。

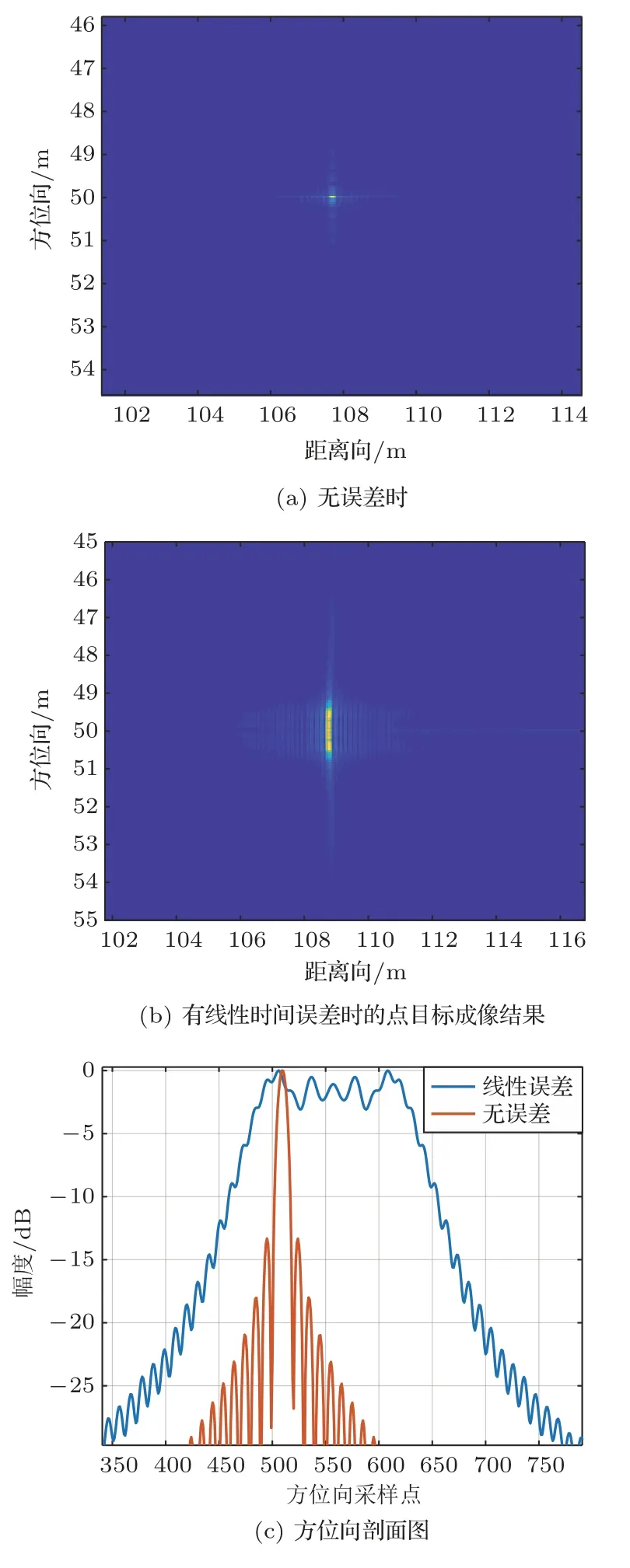
图8 线性时间误差对成像性能的影响Fig.8 Image affected by linear time error

表1 仿真参数表Table1 Simulation parameter table

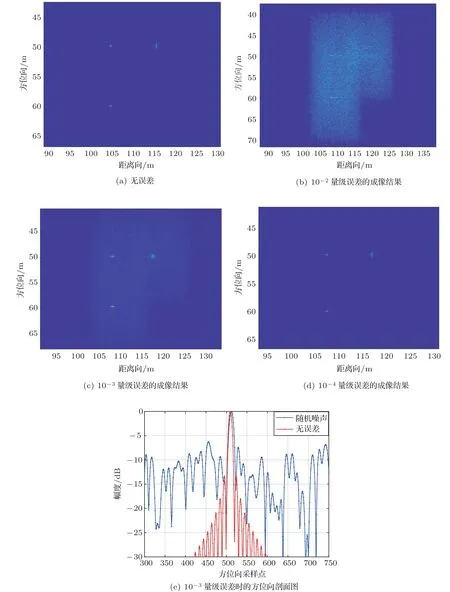
图9 随机时间误差对成像性能的影响Fig.9 Image affected by random time error

从图8中可见，线性时间误差影响距离向和方位向聚焦性能，距离向引起目标图像偏移和分辨率降低，更为明显的是方位向聚焦模糊，主瓣展宽，旁瓣升高，分辨率降低，成像效果不佳。

利用表1中仿真参数对3 个点目标进行RD 算法成像仿真，加入不同量级的随机时间误差，分别加入10-2、10-3、10-4量级的随机噪声，得到的成像仿真结果如图9所示。

从图9可以看出，随机时间误差影响距离向和方位向调频特性，使旁瓣升高，积分旁瓣比增大，目标受到周围噪声干扰影响增大，甚至可能被淹没，因此应用时需要对频率源的时间稳定度提出相应的性能指标要求。

4 结论

本文开展了Bi-SAS 时间同步误差影响的理论分析和仿真验证，计算了误差影响下的距离和方位向分辨率，分别分析了固定时间误差、线性时间误差以及随机时间误差对点目标成像性能的影响。固定时间误差主要引起目标距离向聚焦位置偏移，对方位向聚焦影响不大，但当采样窗无法完全采样时，会出现干扰点；线性时间误差对方位向成像性能影响严重，造成聚焦位置模糊和分辨率下降；随机时间误差不具有累积性，影响距离向与方位向调频特性，造成旁瓣升高。