水下对空中声源的运动参数估计*
2020-06-08刘凯悦彭朝晖张灵珊王光旭
刘凯悦 彭朝晖 张灵珊 王光旭
(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
人们很早就发现利用水下水听器可以接收到附近上空的飞机噪声。自20世纪50年代起,很多国内外学者致力于空中运动声源激发水下声场及水下对空中运动声源的探测研究,先后取得了一系列成果。对空中运动声源透射入水的理论研究方面,Kazandjian 等[1]借助简正波理论对空中运动声源激发的水下声场进行建模,该时域简正波表达式比较复杂,近场计算存在较大误差。Schmidt 等[2]推导出分层波导中声源和接收器联合运动时多普勒频移场的谱表达式,可借助波数积分和简正波的方法进行实现。Lai 等[3]对分层介质中运动声源三维散射场的谱和简正波表达式进行了推导,这一新的模态公式考虑了多普勒频移引起的模态形状变化。为了表示空中高速运动声源水下接收声信号在近场的时变特性,张翼鹏[4]在波数积分模型基础上给出了水平分层介质中,空中单频运动点源激发的水下声场时域解。
水下对空中运动声源的探测方面,Kutakov等[5]利用拖曳水听器在水下探测到水平距离为150~160 m的飞机噪声线谱。Buckingham等[6]利用空中、水下和海底布放的传感器接收水面正上方附近的飞机辐射噪声,接收声信号中观察到明显的多普勒频移特征,且空气中接收信号的多普勒频移远大于水下和海底。Ferguson 等[7]利用海面下20 m 深的拖曳阵在深海环境下成功探测到远至4.6 km 的飞机,并利用射线理论分析了直达波和海底反射波的多普勒频移特征。周伟[8]利用矢量水听器实现对直升机的远距离探测,并在接收信号中观察到由水下声波和侧面波对应的两条具有不同多普勒频移的线谱。
上述工作多是借助空中运动声源的线谱及其多普勒频移特征进行水下探测。由于空中声源的运动速度普遍大于水下声源,因此空中运动声源水下接收声场的多普勒频移更为明显。很多学者依据此特性估计空中运动声源的相关参数,该工作对于判别空中及水下声源、空中声源定位等具有重要意义。
Ferguson 等[9]通过非线性最小二乘法将多普勒频移测量值与预测值相拟合,提出了一种单传感器估计匀速运动目标参数的算法,该经典估计方法被广泛应用于空中传感器对空中运动声源的参数估计(估计参数包括声源速度及静止频率、声源与接收器最小水平距离(Minimum horizontal range,MHR)以及声源经过最近点(Closest point of approach,CPA)时对应的时刻)。在此基础上,很多改进方法被相继提出。Lo 等[10]进一步将上述单传感器方法推广到多传感器及多种阵型,通过结合多个传感器的信息得到更为精确的运动参数估计结果;Xu等[11]和Liang等[12]分别利用多项式线性调频变换(Polynomial chirplet transform,PCT)和多普勒线性调频变换(Doppler chirplet transform,Doppler-CT)等时频分析方法提高瞬时频率(Instantaneous frequency,IF)的提取精度,通过实测货车噪声数据验证了该方法对声源运动参数估计的有效性。在水下对空中运动声源的参数估计方面,Ferguson 等[13]和Lo 等[14]相继利用单水听器、多水听器阵列估计空中声源的运动参数。然而由于空-水介质阻抗的巨大差异,空中声源透射入水后能量损失较大,因此实验中飞机的航行范围仅局限在水听器正上方附近。
综上所述,有关水下对空中运动声源的研究多集中在理论和探测方面,在此基础上,参数估计工作大多围绕Ferguson提出的经典方法进行展开,但水下对空中运动声源的实验验证相对较少,且实验中声源多局限于水下接收器正上方附近。2018年1月,在南中国海北部进行了一次水下水平阵对空中直升机的探测实验。实验过程中,声源近似做匀速直线运动,距接收阵最近距离约3 km,最远距离约16.8 km。利用Ferguson 提出的经典方法成功提取到空中声源的运动参数,并在此基础上实现了声源测距与定位,测距误差在15.8%之内。
1 空中运动声源激发水下声场的多普勒频移特性
空中声源的辐射噪声谱包括宽带连续谱和窄带线谱,其中线谱能量高于连续谱。空中声源一般处于高速运动状态,其速度明显高于水下声源,因此,空中运动声源激发水下声场的线谱多普勒频移效应更为显著。
在水平分层介质中,假定空中声源沿x轴正方向以速度vs做匀速直线运动,在t= 0 时刻经过z轴,声源频率设为Ω0,接收器位于水下(x,y,z)处,且始终保持静止状态。那么相应的水下接收声场由式(1)给出[4]:
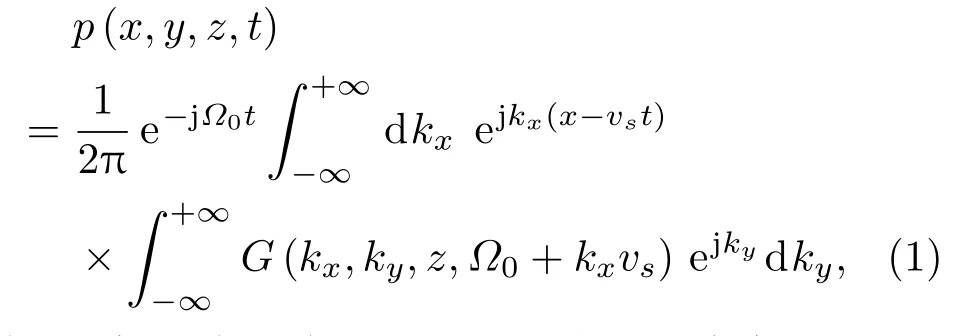
式(1)中,p表示声压,kx和ky分别对应在x和y方向上的水平波数分量。G(kx,ky,z,Ω0+kxvs)表示二维格林函数,由于声源与接收器之间的相对运动引入了多普勒频移,这一项可通过直角坐标系下的OAST(OASES transmission loss module,其中OASES:Ocean acoustic and seismic exploration synthetics)计算程序[15]求解得到。
为具体说明空中运动声源激发水下声场的多普勒频移特性,下面结合深浅海两种水文环境,仿真分析空中声源处于两种不同运动路径下的水下声场。为便于与第4 节中实验数据的多普勒频移进行对比,此处选取与实验相同的声源参数。两种环境下均设置声源高度为93 m,速度49 m/s,声源频率为8.56×10-3(由于实验中运动声源频率的敏感性,因此文中用归一化后的频率值代替)。深海环境设置典型的深海不完全声道声速剖面,海深4500 m;浅海环境参数与实验保持一致,海深93.4 m,海水声速剖面在第4节图11中给出。其他的环境参数如图1所示。
假设声源保持匀速直线运动,初始时刻t=0 s,考虑图2所示的两种声源运动路径:
(1)声源从远场2.45 km 处逐渐靠近接收器,经过距接收器最近点而后远离至远场2.45 km 处(MHR = 0);
(2)声源从远场2.45 km 处逐渐靠近接收器,经过距接收器最近点而后远离至远场2.45 km 处(MHR = 1 km)。
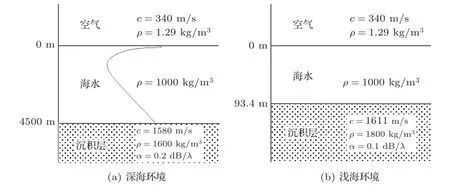
图1 OAST 环境参数设置Fig.1 OAST environment parameter settings
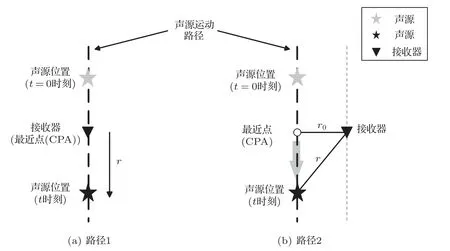
图2 声源运动路径Fig.2 Motion path of sound source
针对上述模型,利用OAST计算程序进行仿真。首先对深海、浅海环境分别选取两种接收深度,深海取1 m、100 m;浅海取1 m、93.4 m。然后计算空中运动声源激发的水下声场,并对声场进行时频分析,两种路径下的时频结果分别如图3、图4所示。
当接收深度远小于声波波长时,空中声源激发的水下声场由侧面波占主导地位。侧面波是空气中的声波在空-水界面发生全发射时,在水下激发的声场。其幅度随着接收深度的增加呈指数递减,因此只在小接收深度下发挥作用。对比图3(a)与图3(b),深海环境下,水深1 m处的接收信号主要由侧面波构成,其多普勒频移(图3(a)中黑色实线)等同于空气中接收信号的多普勒频移。随着深度的增加,侧面波幅度迅速衰减,因此水下100 m深度处的接收信号主要由水下折射波构成,其最大多普勒频移(图3(b)中蓝色虚线)远小于侧面波。对比图3(c)与图3(d),浅海环境下,水深1 m处的接收信号同时包括侧面波以及与海底、海面发生作用的水下折射波。其中侧面波为主要成分,且多普勒频移(图3(c)中黑色实线)远大于水下折射波(图3(c)中蓝色虚线)。同样,水下93.4 m深(海底)的接收信号主要成分变为水下折射波(图3(d)中蓝色虚线)。
图4中接收信号的成分及其多普勒频移随深度的变化规律与图3相一致。不同之处在于,图4中声源与接收器的最小水平距离MHR 为1 km。随MHR 的增大,相同时间间隔内声源与接收器连线同声源运动方向之间的角度变化率减小,导致CPA点附近的多普勒频移变化率减小。因此,相比于图3,图4中瞬时频率的变化速度在CPA 点附近较为缓慢。此外,在图4(b)中还发现了由海底反射波成分引起的多普勒频移,由于远场情况下,空中声源的水下声场幅度呈现出余弦方向性的特征,因此海底反射波的幅度大于水下折射波。
实际情况下,空中声源运动路径很难恰好经过水下接收器正上方,相比之下,二者常处于远场,可近似对应第二种运动路径。下面选取浅海环境模型,并令声源与接收器对应第二种运动路径(MHR = 1 km),取接收深度分别为30 m、40 m、50 m、60 m、70 m、80 m,比较不同接收深度下的水下声场强度及多普勒频移变化量。六种深度下的接收声场声压级及瞬时频率随时间的变化曲线分别如图5(a)、图5(b)所示。
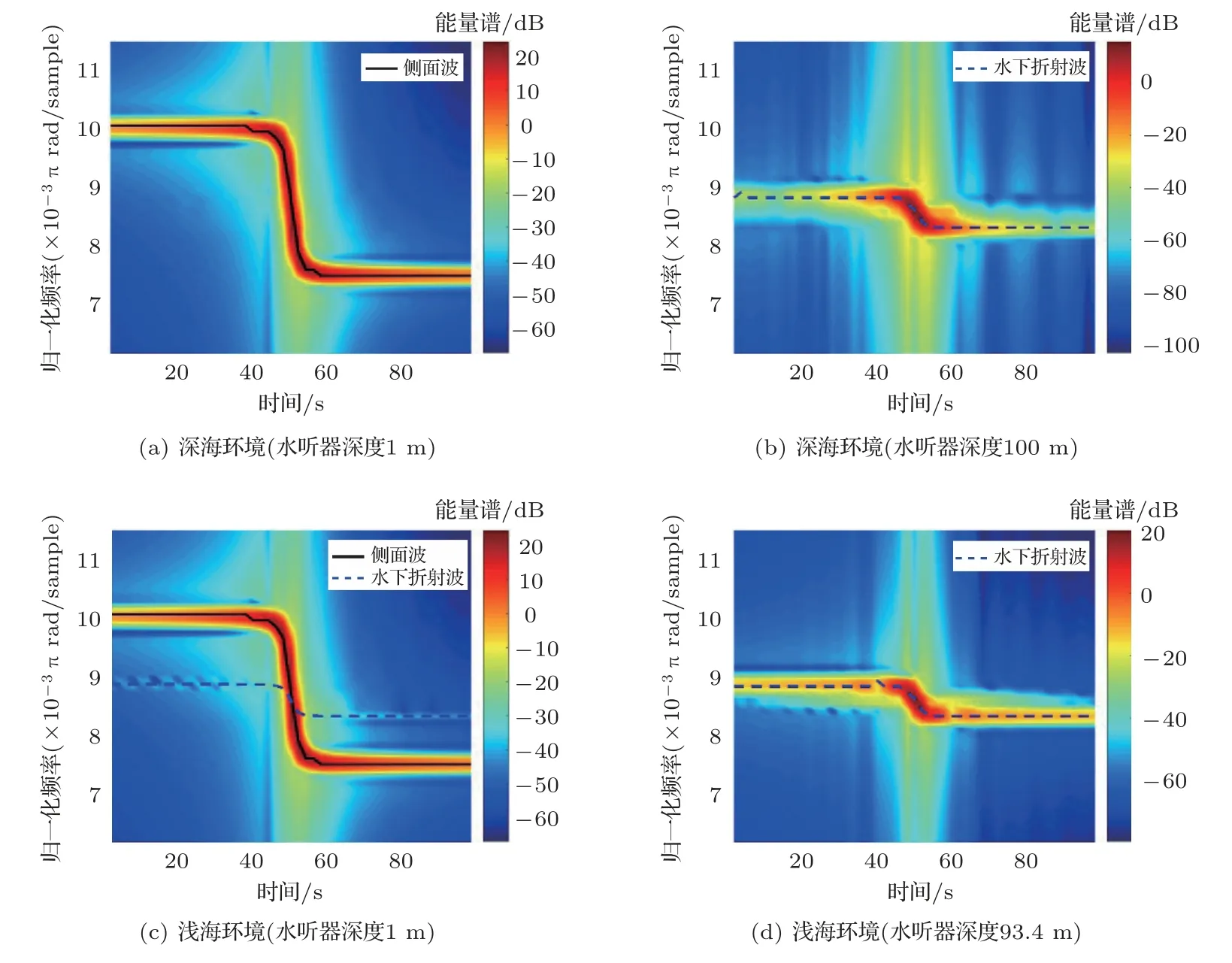
图3 时频图(路径1)Fig.3 Spectrogram (Motion path 1)
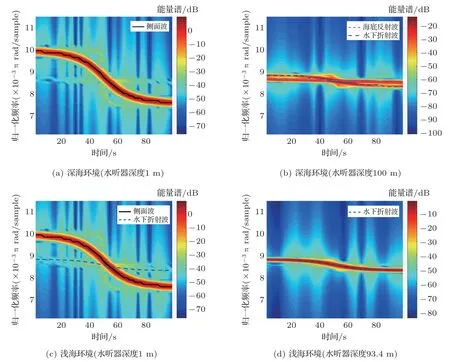
图4 时频图(路径2)Fig.4 Spectrogram (Motion path 2)
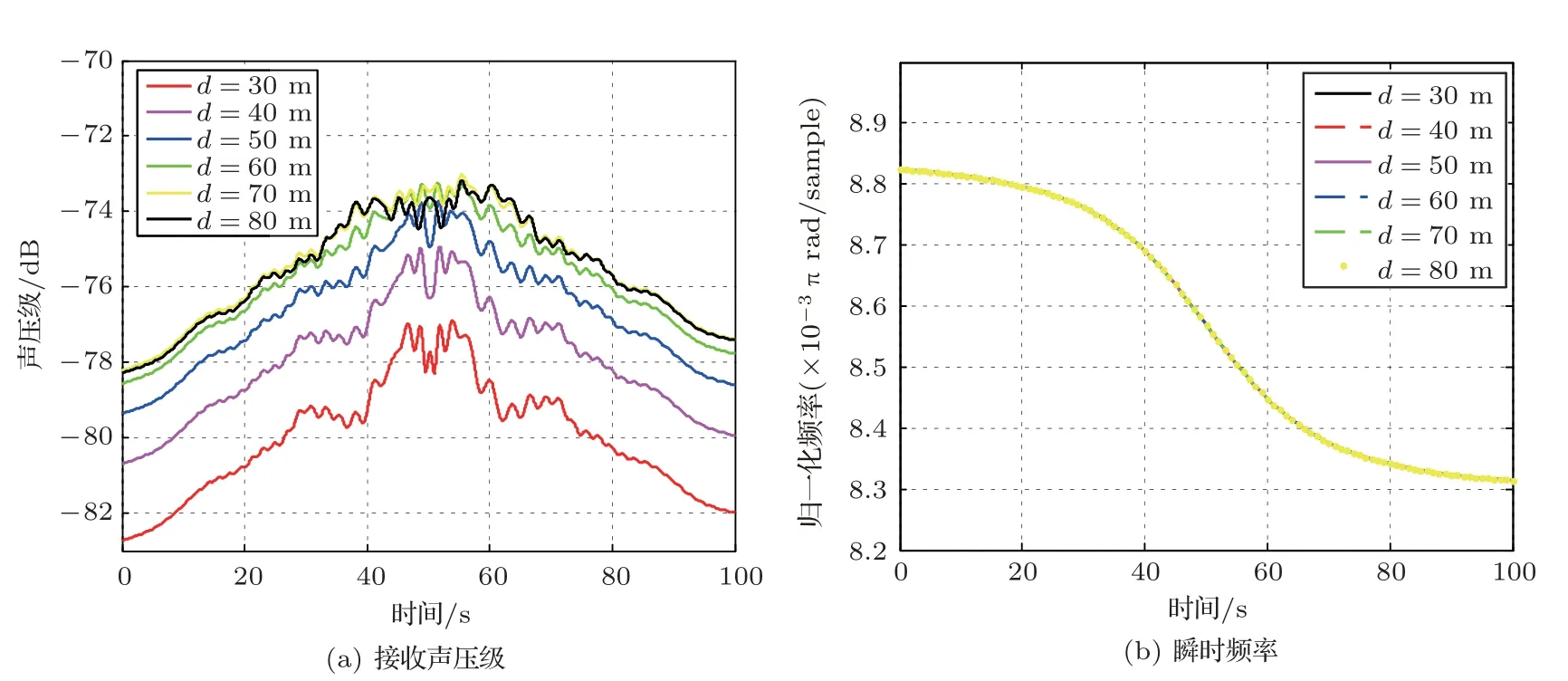
图5 不同接收深度的声场变化Fig.5 Acoustic field variation at different receiving depths
观察图5(a)发现,对不同的接收深度,水下声场的声压级会有所不同,在上述所给深度下,接收声压级最大相差5 dB 左右。随接收深度的增加,水下声场的能量基本呈现出递增的趋势,这是由于远场情况下,空中声源激发水下声场的余弦方向性所致。观察图5(b)发现,由于声源与接收器的最小水平距离MHR 远大于不同接收深度之间的差异,在CPA点附近相邻时段内声源发出的声信号到达不同深度接收器的时间差基本相同,因此不同深度的接收信号呈现出几乎一致的多普勒频移变化规律。
在了解空中运动声源激发的水下声场规律的基础上,可利用接收声场中的多普勒频移信息,借助Ferguson 提出的经典方法解决水下对空中声源的运动参数估计问题。
2 空中声源的运动参数估计模型
考虑图6所示多普勒频移模型[9]:空中声源以恒定速度v、恒定高度L沿直线运动,在tc时刻经过接收器正上方,声源辐射频率f0为定值。声源运动期间,接收器始终保持静止状态。此时,接收信号在t时刻的瞬时频率由式(2)给出:
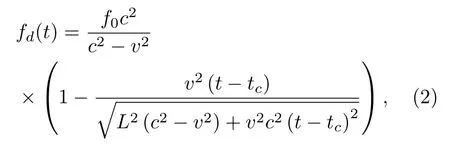
式(2)中,待估计的运动参数为{tc,f0,v,L},分别对应声源经过最近点时刻、声源静止频率、声源运动速度以及声源与接收器最小水平距离。
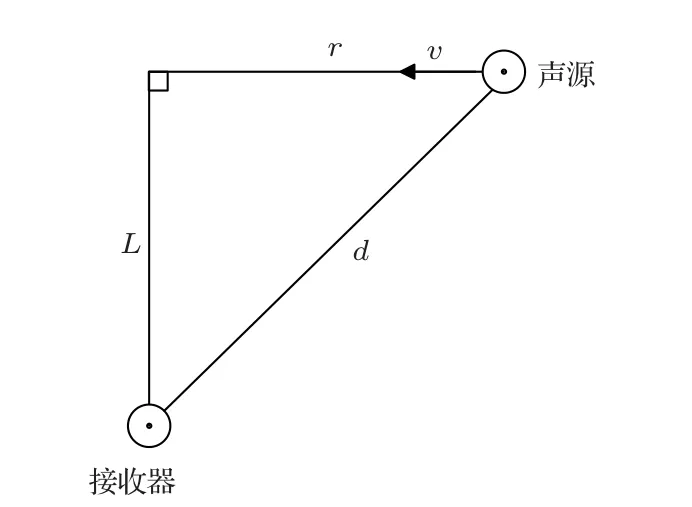
图6 多普勒频移模型Fig.6 Doppler frequency shift model
公式(2)可精确表示同一介质中,运动声源激发的接收声信号的多普勒频移,其中,L表示为声源与接收器的最近水平距离。当声源和接收器分别位于空气、水两种介质中时,在远场假设下(声源与接收器的水平距离远大于声源与接收器的垂直距离),可将空气声源近似看作水下声源,此时,可用式(2)近似表示空中运动声源激发水下声场的多普勒频移,式(2)中的声速c表示海水声速。
对式(2)做如下变换,
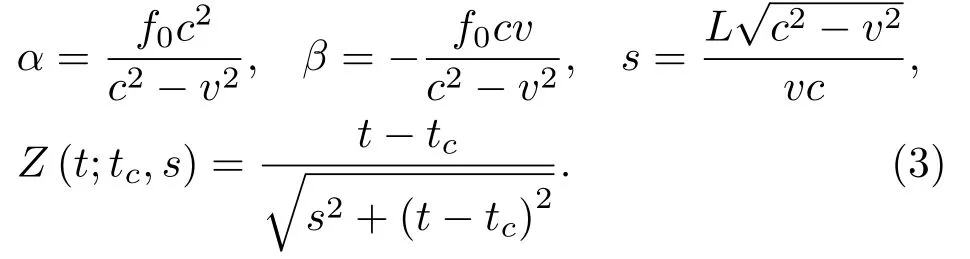
则式(2)也可写作式(4):
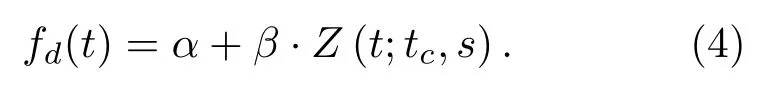
由此,运动参数可由{tc,f0,v,L}等效转换为{tc,α,β,s}。等效运动参数的估计可通过非线性最小二乘法进行。
局部情况:伤口敷料渗出,呈淡红色血渍印,更换敷料加压包扎后短时间内仍出现上述症状。有些患者伤口敷料虽清洁干燥,但伤口周围皮肤出现隆起,触及有波动感,提示皮下有脑脊液渗出。脊柱手术后24 h伤口引流量增多,有时多至1 000 ml以上,颜色呈淡红色或清亮液体(正常<300 ml,呈血清样混浊液)。
综上所述,给出运动参数估计的具体步骤如下:
(1)对接收声场进行时频分析,获取信号在tj(j=1,2,···,N)时刻的瞬时频率g(tj)(默认瞬时频率提取方法为峰值检测法,即将tj时刻的频谱能量最大值对应的频点视为此时刻的瞬时频率)。
(2)通过瞬时频率的理论公式(式(2))计算瞬时频率预测值fd(tj)。
(3)利用最小二乘拟合估计等效运动参数,即求解式(5):
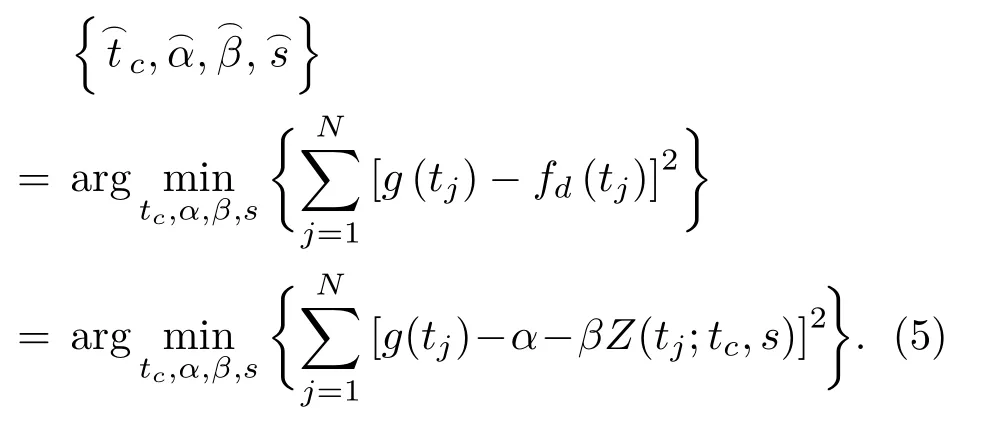
(4)利用式(3)对步骤(3)所得参数进行转换。最终得到声源的运动速度、声源与接收器最小水平距离、声源静止频率,分别由式(6)给出:
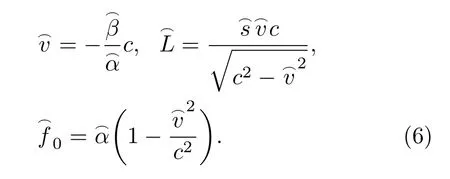
3 算法仿真
空中高速运动目标的声源谱级一般在134~154 dB re 20 μPa (160~180 dB re 1 μPa)左右,海洋环境噪声谱级在50 Hz 中等航运3 级海况时约85 dB,检测阈取3 dB。在分别获取得到10 dB时间增益和15 dB 空间增益的情况下,被动声呐的优质因数为97~117 dB。选取图4(d)对应的声场仿真模型进行具体分析,当声源与接收器之间的水平距离为2 km左右时,空中声源激发的水下声场在所给声源频率下对应的传播损失约112 dB。忽略空中声速剖面、粗糙海面等因素的影响,可得接收信噪比约-15~5 dB。
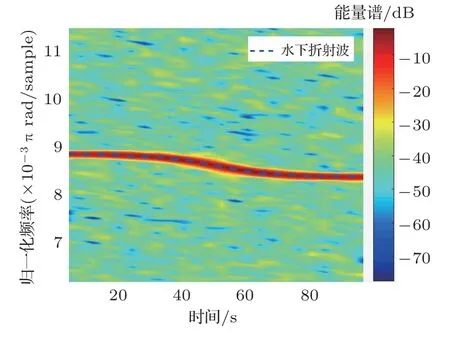
图7 时频图Fig.7 Spectrogram
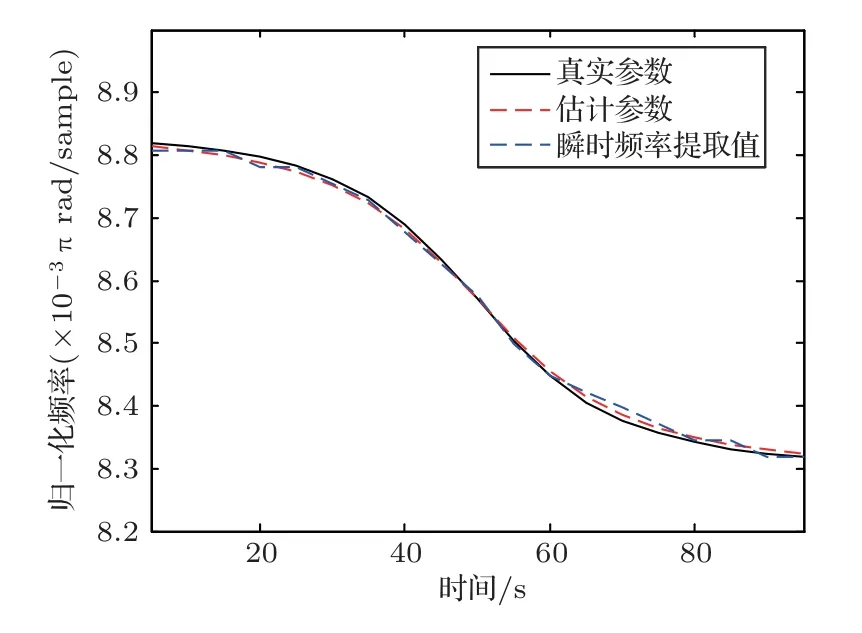
图8 瞬时频率IF 提取曲线Fig.8 Instantaneous frequency extraction curve
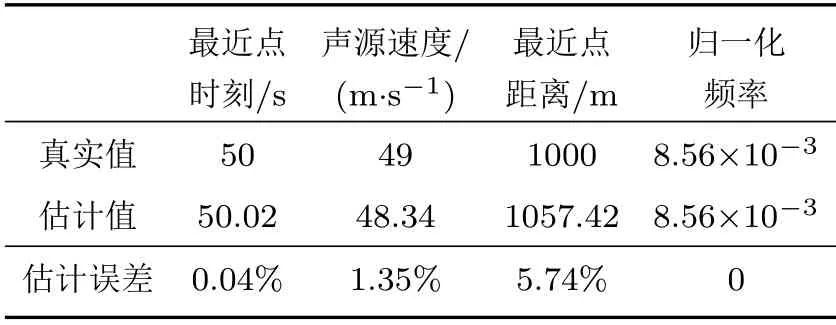
表1 运动参数估计结果Table1 Results of motion parameters estimation
观察图8,蓝色虚线是通过峰值检测提取到的瞬时频率,对应图7中的蓝色虚线。将运动参数估计结果代入公式(2)中计算多普勒频移预测值,并绘制为红色虚线。两条虚线近乎重合,可证明非线性最小二乘法进行参数估计的准确性。此外,将由真实运动参数计算得到的瞬时频率绘制为图8中黑色实线,对比黑色实线与蓝色虚线可以发现,瞬时频率提取的误差是造成运动参数估计误差的主要因素。在信噪比较高的情况下,可结合PCT[13]、Doppler-CT[14]等时频分析方法提高时频分析的聚焦性,从而提高瞬时频率提取的精度。
4 实验分析
4.1 实验数据处理
下面通过实验数据进一步验证算法的准确性,并进行误差分析。
2018年1月,在南中国海北部海域进行了一次水下对空探测实验,实验示意图如图9所示。实验以直升机作为空中运动声源,采用一个由53阵元组成的海底水平阵接收声信号。实验期间,声源近似做匀速直线运动,声源速度保持在49 m/s 左右,距海面高度约93 m。图10给出了声源与接收阵的水平距离随时间的变化曲线,从图中可以看出,声源从远场16.8 km 处逐渐靠近接收阵,经过距接收阵最近点后远离至远场5 km处,声源与接收阵的最近点距离MHR约为3 km。实验期间海水的声速剖面如图11所示,水深20 m 以上及60 m 以下呈弱正梯度分布,20~60 m 之间呈负梯度分布,声速变化不超过5 m/s。实验海区海底整体比较平坦,平均海深94 m。
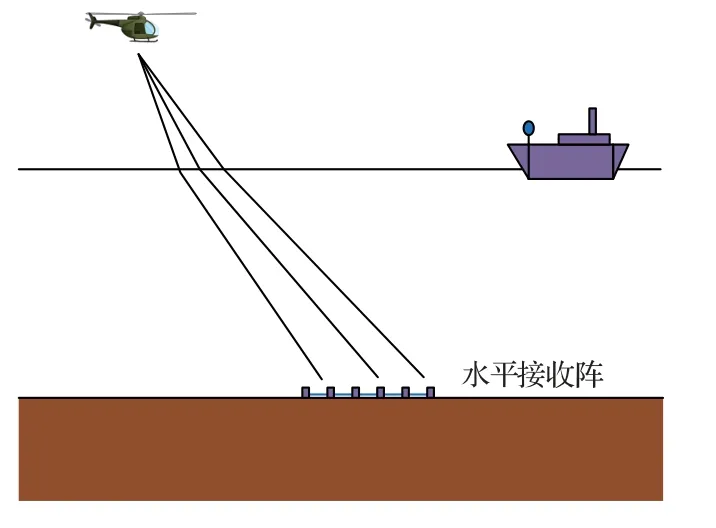
图9 实验示意图Fig.9 Experimental schematic diagram
由于声源与接收阵之间的距离较远,加之水面源的干扰,空中运动声源激发的水下声场信噪比较低,仅利用单个阵元无法精确提取到空中声源的瞬时频率,因此需要借助整个接收阵的信息进行后续处理。首先,利用最小方差无失真响应(Minimum variance distortionless response,MVDR)波束形成器获取空中运动声源在不同时刻处的方位信息,累计时间绘制方位历程图,如图12所示,其中黑色实线与蓝色虚线分别对应空中声源方位的真实值与估计值。而后,利用此方位历程,通过MVDR 进行空域滤波处理,并进行时频分析得到空中声源的LOFAR 谱图,在图13中给出。提取图13中的瞬时频率曲线,并在图14中将其绘制为黑色实线。为避免峰值检测过程中引入的瞬时频率提取误差,将黑色实线进行平滑处理,得到蓝色虚线。可以看出,蓝色虚线更符合声源在当前运动路径下对应的瞬时频率逐渐减小的变化趋势。为了对比,红色实线给出了由空中声源的真实方位历程计算得到的瞬时频率曲线,在最后50 s时间内,真实方位与估计方位所对应的瞬时频率值相差较大。
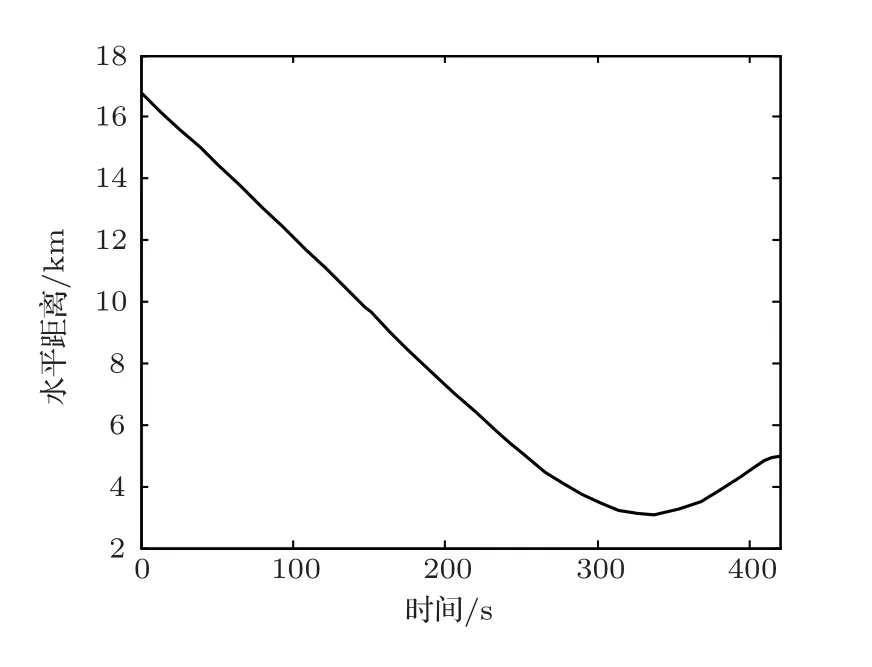
图10 声源与接收阵的水平距离随时间变化曲线Fig.10 Horizontal distance curve with time of source and received array
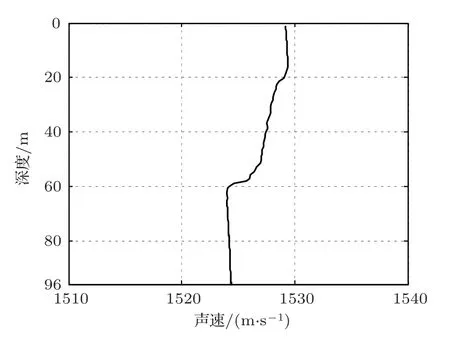
图11 声速剖面Fig.11 Sound velocity profile
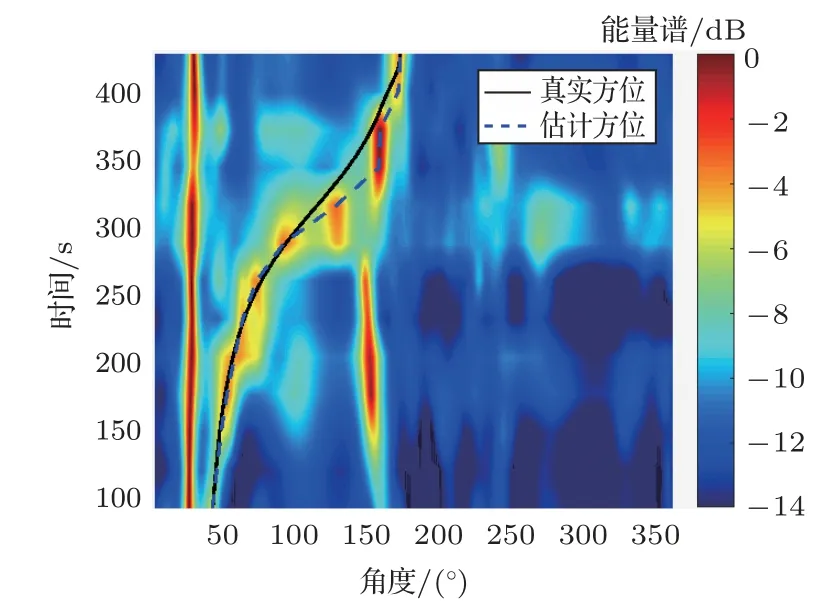
图12 方位历程图Fig.12 Bearing-time records
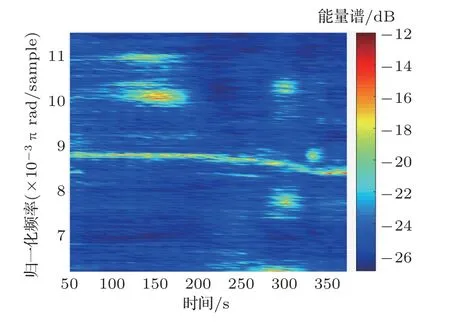
图13 空中声源LOFAR 图Fig.13 LOFAR of airborne source
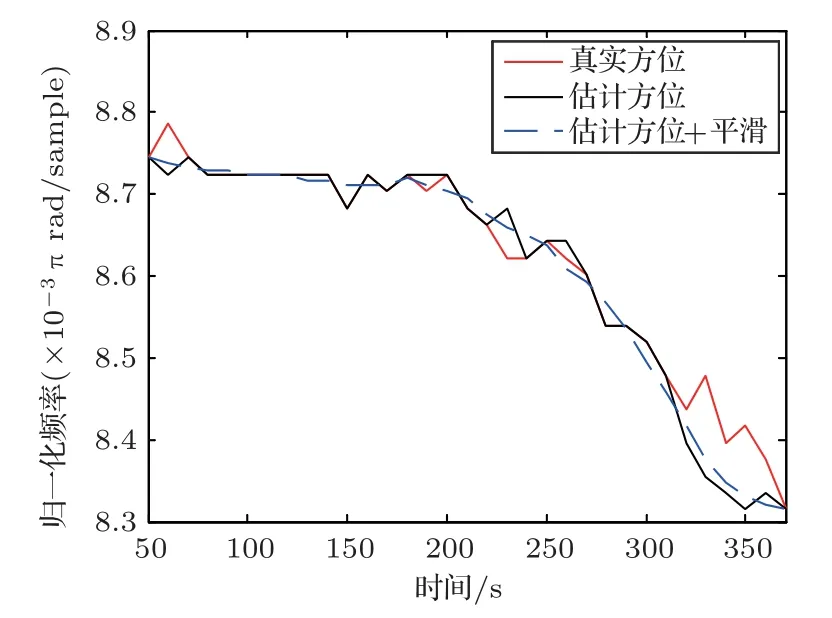
图14 瞬时频率IF 提取曲线Fig.14 Instantaneous frequency extraction curve
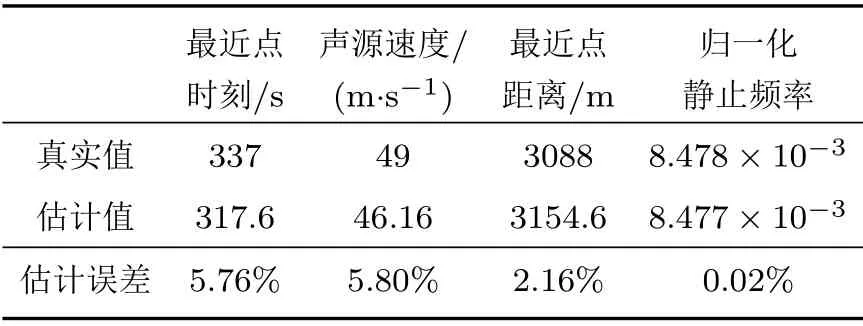
表2 运动参数估计结果Table2 Results of motion parameters estimation
利用图14中蓝色虚线所对应的瞬时频率信息进行空中声源的运动参数估计,估计结果见表2。四个参数的估计误差均在6%之内,其中声源距接收阵最近时刻tc、声源速度v的估计误差较大,产生这一误差的原因将在4.2 节中给出。通过对声源速度的估值约46 m/s,可以大概率地判断声源为空中声源。
此外,利用估计得到的参数{tc,v,L},给定任意时刻t,可通过勾股定理计算声源与接收阵之间的距离。最后结合方位估计结果,完成对空中运动声源的定位。上述途径所得的测距和定位结果分别如图15、图16所示,两图中均用黑色实线表示GPS 测得的真实结果,用蓝色虚线表示估计结果。从图15中可以看出,最近点时刻tc的估值偏差对测距结果的影响较大,与真实距离相比,估计距离整体向左偏移,最大测距误差为15.8%。从图16中也可看出声源位置的整体偏移。
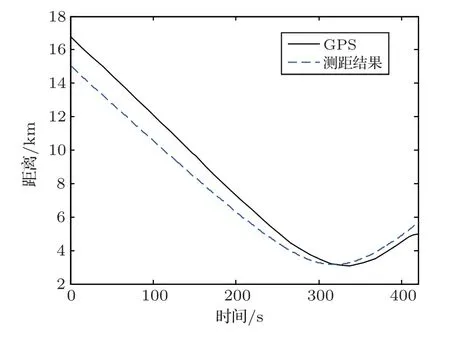
图15 测距结果Fig.15 Ranging results
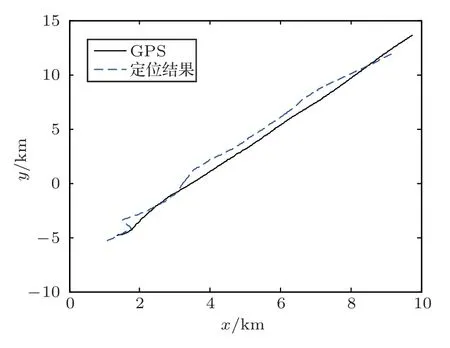
图16 定位结果Fig.16 Positioning results
4.2 误差分析
实验数据处理发现,由于在个别时刻处对空中声源的方位估计存在偏差,导致对瞬时频率的提取不够准确,最终为运动参数的估计引入误差。将图12中声源方位的真实值与估计值进行对比,分别用黑色和蓝色实线表示,如图17所示。可以发现,在第315 s和343 s两个时刻处,二者相差较大,这是由于两个时刻恰好对应声源经过距接收阵最近点附近。此时,声源方位变化率较大。而为保证接收声信号的时间增益,在方位估计过程中对信号所取窗长度(为70 s)较大,由此引入角度估计误差。究其原因,是空中运动声源的水下接收声场信噪比较低,从而产生了一系列误差。
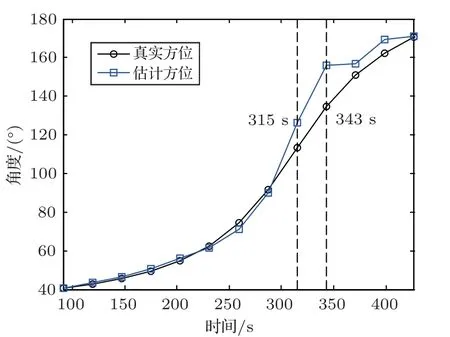
图17 真实方位与估计方位对比Fig.17 Comparison of real azimuth and estimated azimuth
综上,给出算法的适用性条件如下:
(1)声源与接收器之间的水平距离远大于声源高度,从而可以忽略高度的影响,直接应用式(2)求解空中运动声源激发水下声场的瞬时频率预测值;
(2)声源运动路径包含距接收器最近点附近,使接收声场具有足够的多普勒频移信息;
(3)为保证瞬时频率估计的准确性,接收声场应具有一定的信噪比,可借助多阵元的阵增益进行提高。
5 结论
空中声源的运动速度远大于水下声源,使得空中运动声源的水下声场具有较大的多普勒频移。利用空中运动声源激发水下声场的瞬时频率信息,结合非线性最小二乘法可估计得到声源的运动参数(声源运动速度、静止频率、声源与接收器最小水平距离以及声源经过最近点时对应的时刻)。通过数值仿真与浅海实验,证明了Ferguson提出的经典方法应用于水下对空中运动声源参数估计的正确性。实验处理结果表明:(1)声源速度估值约46 m/s,大概率判定为空中声源;(2)利用运动参数估计结果对空中声源进行测距及定位,测距误差在15.8%之内。
致谢感谢参与本次实验的全体实验人员,是他们的辛勤劳动提供了宝贵可靠的实验数据。
