某型振动轮噪声数值模拟及优化分析*

2020-06-08苏俊收刘汉光

应用声学 2020年2期

苏俊收庄超李军刘汉光

(1 江苏徐工工程机械研究院有限公司徐州 221004)

(2 高端工程机械智能制造国家重点实验室徐州 221004)

0 引言

振动轮是道路施工建设中必不可少的工作装置。振动轮工作时，振动轮内的偏心轮高速旋转，成为强烈的振动源，振动轮表面振动而产生本体噪声，并以声波的形式向四周辐射。经过实验测试，振动轮不发生振动时驾驶室司机耳旁噪声值为72 dB(A)，振动轮振动时该噪声值为76 dB(A)。运用声压级累加公式，计算出振动轮对驾驶室噪声的贡献量约为60%，振动轮噪声已经成为工程车辆最大噪声源，而且当振动频率与结构的自身固有频率一致或相近时会产生共振，造成结构件加速损坏以及增大司机耳旁噪声值。

目前，国内外对振动轮的研究主要集中在减振系统、压实性能、采用经验公式来选用减振器刚度等[1]，还没有看到系统地对振动轮辐射噪声进行预估研究的报道，而且振动轮不同激振形式、不同激振频率对噪声的影响至今还没有定量的分析。本文以某型号工程车辆的振动轮为研究对象，对振动轮辐射噪声进行了数值模拟，并比较了垂直振动与圆周振动两种不同激振形式对辐射噪声的影响，而且通过调整激振频率，降低了振动轮噪声。本文为振动轮的低噪声设计提供了参考依据。

1 理论分析

振动轮激振器工作原理就是利用其高速运转偏心块的离心力作用，根据给定的偏心矩和振动工作频率，计算其激振力，振动轮参数如表1所示。

振动轮离心力计算公式为

其中，F为离心力，m为质量，r为旋转半径，w为角速度，f为频率。

计算得出F= 173923.3 N，由经典动力学理论可知，振动轮频率响应公式为

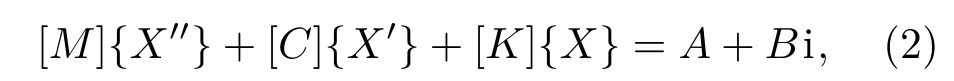
由于振动轮是连续体，通过有限元方法将振动轮离散化，可求解动力学方程，得出振动轮各单元的振动速度X′。

通过实验测得振动轮上振动及附近测点的噪声，运用相干函数公式，计算出相干系数如图1所示。

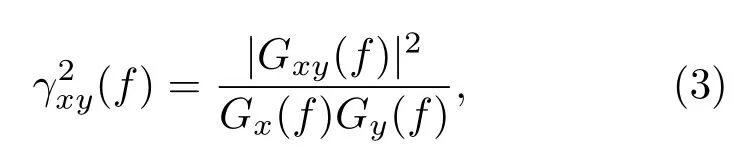
其中，Gx(f)是振动信号的自谱密度函数，Gy(f)是噪声信号的自谱密度函数，Gxy(f)是振动与噪声信号的互谱密度函数。

从图1中可以看出，在35 Hz 处，声振相干系数达到了0.95 以上，即可以认为35 Hz 上的噪声是由振动产生的。

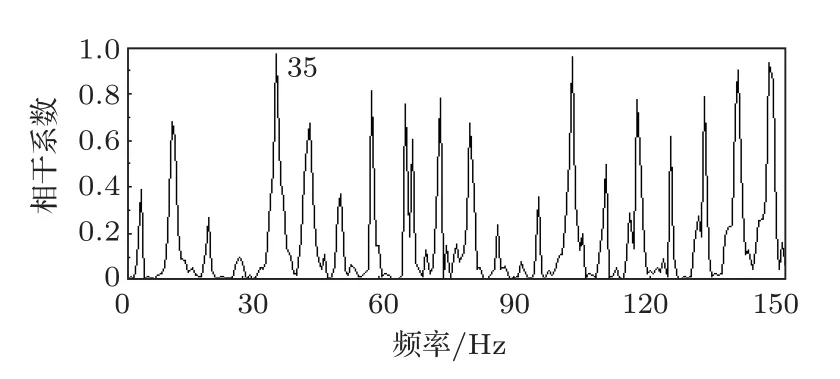
图1 振动与噪声信号的相干系数Fig.1 Coherence coefficients of vibration and noise signals

对于振动轮表面辐射声场而言，可以认为空气中的声波对振动轮表面振动没有影响，所以不进行耦合场计算。由于振动轮的网格是完全封闭的，根据各种声学计算方法的特点，结合振动轮模型的实际情况，选用直接边界元法预估振动轮辐射噪声声场。

将计算得到的X′带入下列Kirchhoff公式中，即可得到空间中任意点的声压值：

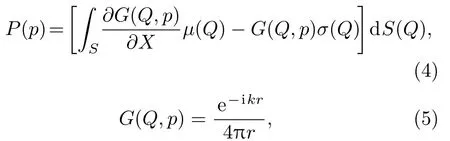
其中，G(Q，p)为格林函数，r=|Q-P|，Q为振动轮表面S上的任意点，P为空间中任意点。

单层势σ代表振动轮表面S处的速度脉动，即

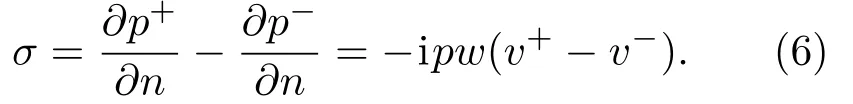
双层势μ代表声学边界元表面S处的声压脉动，即

上标“+”和“-”分别代表振动轮表面与辅助虚边界域表面。边界元法声学计算方程矩阵形式为

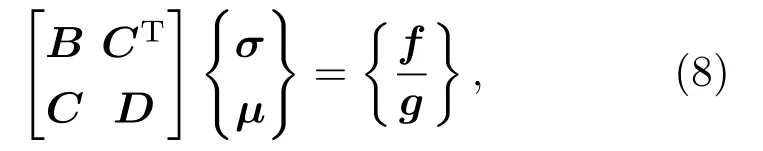
其中，B、C和D为系数矩阵，σ为速度脉动向量，μ为压力脉动向量，f和g是外界激励向量。求解该方程可以得到边界单元各节点的单层势σ和双层势μ。

2 数值模拟

2.1 振动仿真

振动轮是通过减振器连接到框架上的，减振器参数如表2所示。

在ANSYS 软件中，减振器用BUSHING 单元来模拟，对振动轮施加约束。在轴承连接处，施加两个相互垂直、相位差为90°的激振力，= 173923.3 N，模拟振动轮受到的离心力，振动轮有限元模型如图2所示。然后进行35 Hz 振动谐响应分析，结果如图3所示。

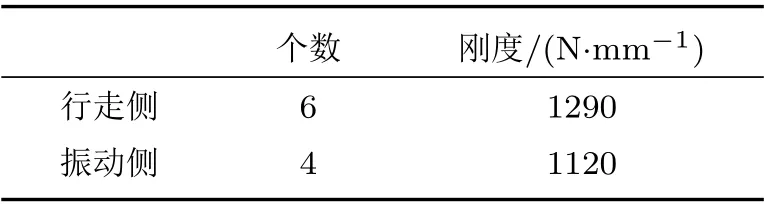
表2 减振器刚度Table2 Damper stiffness

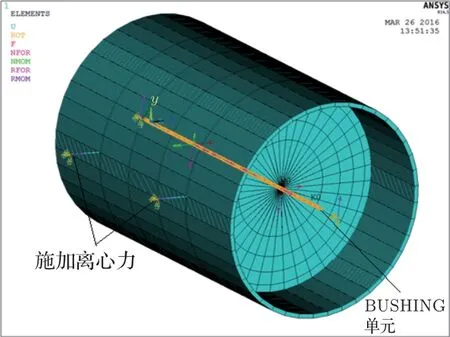
图2 振动轮有限元模型Fig.2 Vibration wheel finite element model

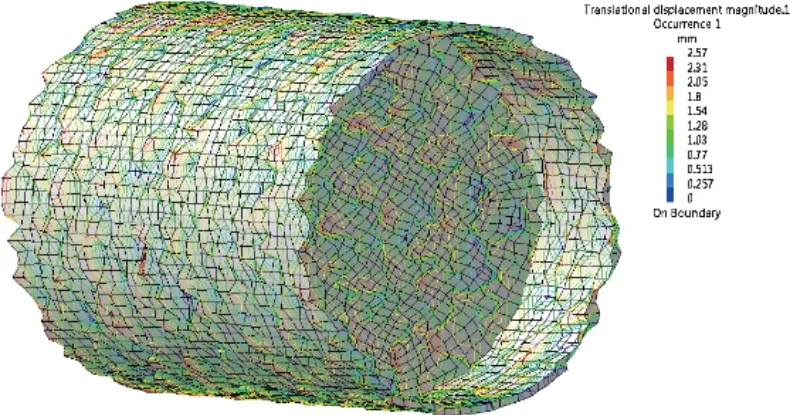
图3 35 Hz 振动轮谐响应分析结果Fig.3 Analysis results of harmonic response of 35 Hz vibration wheel

2.2 噪声仿真

将振动轮的振动响应导入到Virtual.Lab Acoustics 中进行，对振动轮的声场辐射噪声进行仿真预估[2]。如图4所示，建立了振动轮模型的声学边界元网格，将振动轮的振动响应数据映射到声学网格上，得到振动轮模型的声场分布，如图5所示。

图4 振动轮的声学边界元模型Fig.4 Acoustic boundary element model of vibration wheel

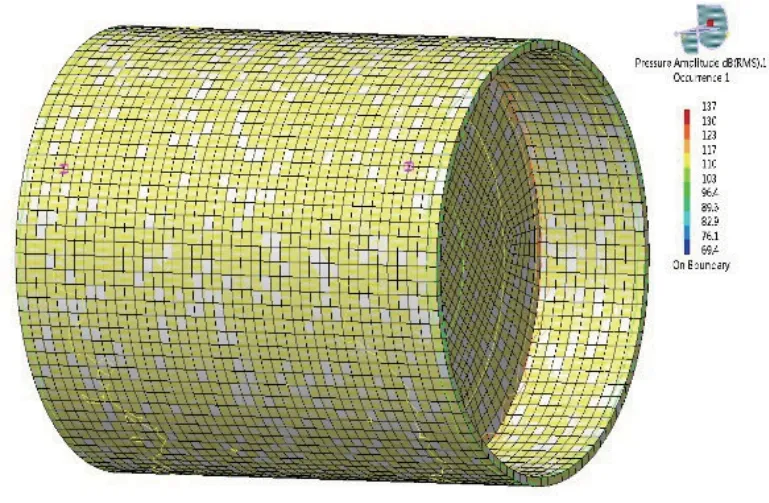
图5 35 Hz 振动轮的声场分布Fig.5 Sound field distribution of 35 Hz vibration wheel

按照GB/T 25612—2010标准，设定测量面半径尺寸为16 m，测量面上设置6 个场点[3]，如图6所示，得到各点的声压值，如表3所示。利用声功率计算公式(9)与公式(10)，计算出振动轮35 Hz 辐射声功率为83.5 dB(A)。

图6 振动轮的场点设置Fig.6 Field point setting of vibrating wheel

表3 35 Hz 场点声压值Table3 Sound pressure of 35 Hz field point

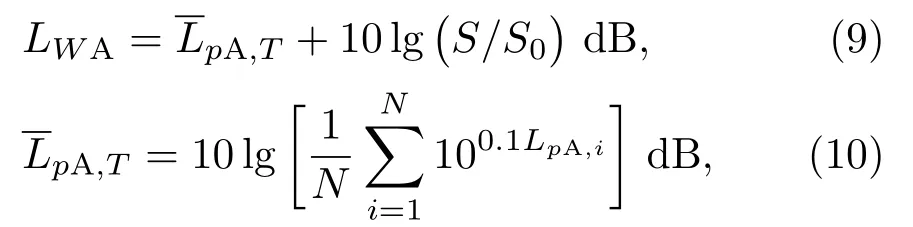
其中，为测量面上时间平均A 计权声压级的能量平均值，S为半球测量面的面积，半径为16 m时，10 lg(S/S0)=32.1 dB。

2.3 实验验证

为了验证声学仿真分析的正确性，对此振动轮辐射噪声进行了实验测试，测试场景如图7所示，得到各点的声压值，如表4所示。

图7 测试现场图Fig.7 Test site diagram

表4 35 Hz 测点声压值Table4 Sound pressure of 35 Hz messure point

计算出振动轮35 Hz辐射声功率为85.1 dB(A)。将实验结果与仿真结果(表3)进行对比，无论各场点的声压值，还是计算出的声功率值，误差都在5%之内，误差主要是由于其他声源的影响。仿真结果和实验结果在一定程度上非常吻合，说明仿真结果具有一定的分析可行性。

3 优化设计

3.1 不同激振形式对噪声的影响

传统的圆周振动是普遍采用的激振形式，如图8所示，这种形式会引起振动轮在水平方向的横向振动，造成振动功率消耗。

近年来，垂直振动发展迅速，它采用的是激振形式，如图9所示，这种形式会使水平方向上的激振力相互抵消，降低能量损失[4]。

图8 圆周振动形式Fig.8 Circular vibration form

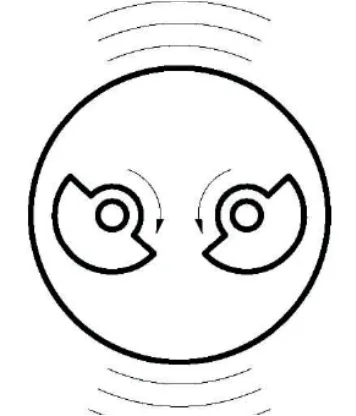
图9 垂直振动形式Fig.9 Vertical vibration form

另外从辐射噪声的角度，垂直振动形式的水平方向振动接近零，几乎不会辐射噪声，大大降低了振动轮的辐射声功率值，为了定量地对比两种不同激振形式辐射噪声值，用前述方法对垂直振动轮进行了噪声仿真预估。根据各测点噪声值计算出振动轮35 Hz辐射声功率为68.4 dB(A)。

垂直振动比圆周振动辐射声功率降低了近15 dB(A)，表明振动轮垂直振动的辐射噪声明显低于圆周振动形式。

3.2 不同激振频率对噪声的影响

在振动轮工作中，明显听到一种共鸣声。为了更好地研究驾驶室空腔声场的声学特性，确定是否为共振引起，建立了空腔的三维声学模型，驾驶室实物如图10所示。

利用LMS Virtual.Lab Acoustics 对空腔模型进行了模态分析[5]，空腔的第一阶固有频率正好为35 Hz，振型如图11所示。因此在振动轮振动时易引起空腔共振，驾驶室噪声较大，因此需要对驾驶室结构或激振频率进行改进优化以避免共振。

图10 驾驶室实物图Fig.10 Cab physical diagram

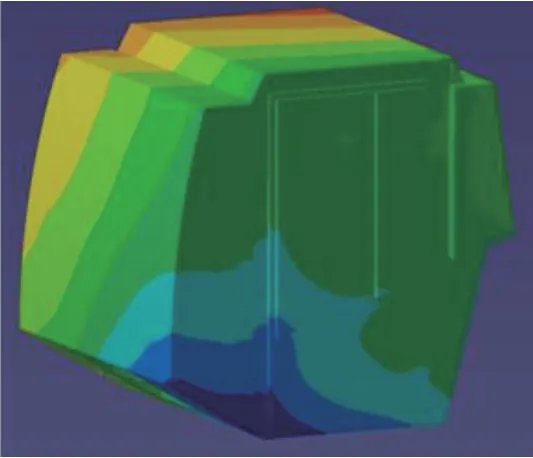
图11 35 Hz 空腔模态振型Fig.11 35 Hz cavity mode

改进驾驶室结构，需要重新开发模具，成本很高，可通过调整振动轮激振频率实现。振动轮的振幅与加速度可通过公式(11)换算：

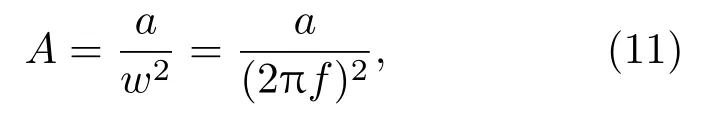
式(11)中，A为振动轮轴承处振幅，a为振动加速度，f为振动频率。

根据牛顿第二定律公式，加速度为

则

其中，m为偏心质量，r为偏心半径，M为振动轮质量。振动轮的振幅与激振频率无关，调整激振频率，并不会影响振幅，但是激振频率的选择，与土壤固有频率有关，不同密实度的土壤固有频率不同。振动轮的激振频率在被压实土壤的固有频率范围内的压实效果最好[6]。根据文献[6]，振动频率在25～50 Hz时可获得最大的压实力。

调研各种型号的振动轮，将振动频率调整到33 Hz，共鸣声消除，经过测试驾驶室司机耳旁噪声值降低3 dB(A)，所以在振动轮设计阶段[7-11]，对零部件结构进行模态分析，需充分考虑结构件是否存在共振。