BRB与结构刚度比对不规则结构抗震的影响分析
2020-06-08陈克伟潘福婷
王 颖,陈克伟,潘福婷
(建筑结构安徽省普通高校重点实验室(安徽新华学院),安徽 合肥 230088)
0 引 言
随着经济发展,在节能、环保、高效的绿色建筑背景下,钢框架结构得到快速发展,结构形式也变得复杂多样。而不规则钢框架结构在地震作用下的安全问题,更应该引起重视。将BRB设置在不规则钢框架结构中,形成BRB支撑不规则结构耗能减震体系,BRB支撑在拉压作用下能够达到全截面屈服而不屈曲[1],可有效地提高结构的延性及抗震能力。不规则结构的抗扭问题成为约束此类结构应用的重要因素。研究BRB与不规则结构的合理刚度比可以更好地控制其扭转和地震作用,对提高其安全性具有很好的实用价值[2]。这种支撑结构体系在保证结构抗震能力的同时,还可有效减少结构的用钢量[3],提高经济效应,促进不规则钢框架结构的发展和应用。
1 BRB-框架结构体系协同工作模式
BRB-框架结构体系是依靠BRB的屈服耗能达到结构抗震设防的目标。在多遇地震作用下,BRB与框架都为弹性状态,实现小震作用下不坏的结构抗震目标;设防烈度地震作用下,BRB进入屈服耗能阶段,框架结构局部发生塑性变形,修护后可以继续使用,实现中震可修的结构抗震目标;罕遇烈度地震作用下,BRB与框架都发生不同程度的塑性变形,可通过合理控制塑性铰发生的位置及发生的顺序,从而实现大震不倒的结构抗震目标。为了达到各级地震作用下的抗震目标,必须依据结构特点进行BRB的合理设计与布置,确定支撑的刚度及布置形式。
2 BRB层间布置形式
BRB的层间布置形式有多种,每种布置形式都有其各自的优缺点,因此需要结合建筑结构的外形、门窗位置、设备功能、支撑的耗能、空间利用及强柱弱梁等受力性能等多方面进行综合考虑。同时BRB沿竖向的布置,也会影响结构的减震性能。通常BRB沿竖向设置在楼层越低的位置,其结构的减震效果越明显,但考虑竖向刚度的不均匀会导致竖向结构的不规则性,BRB最好沿结构竖向所有的楼层均匀设置。BRB的层间布置形式如图1所示。
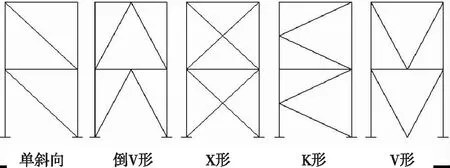
图1 BRB层间布置形式
3 BRB等效刚度计算
BRB是一种新型的支撑类型,由外围约束机制、芯材、无粘结材料3个主要组成单元。在轴向力下,BRB支撑是依靠中间屈服芯材的塑性变形来消耗地震能量的。外围约束套筒可防止内部芯材受压过程中发生屈曲失稳情况,保证其在受拉、受压时均处于全截面屈服的状态。为实现理想的耗能效果,芯材常采用中低强度的钢材,通常芯材的纵向由连接段、过渡段及耗能段共3个部分组成(图2)。

图2 BRB支撑纵向组成
BRB纵向的3段截面面积、刚度都不同,A1、A2、A3分别是连接段、过渡段、耗能段的截面面积。实际工程中,需对BRB进行等效刚度简化处理[4],在计算弹性状态下的BRB等效刚度时通常是忽略其纵向的连接段、过渡段截面改变,芯材按照全长截面面积不变的情况考虑,均为A3,则BRB等效刚度为

(1)
当BRB进入塑性耗能阶段,纵向的过渡段与连接段都处在弹性的范围,而屈服耗能核心段则处于塑性,此时BRB等效刚度的计算不同于弹性状态[5]。
4 BRB与结构抗侧刚度比
BRB-框架结构体系中,BRB与框架共同承担水平荷载,其结构体系的抗侧移能力为BRB和框架结构抗侧移能力之和,其力学模型可表示为3线形(图3)。随着水平荷载的增大,整个体系经历弹性状态、BRB屈服状态、框架整体屈服状态3个阶段。

图3 BRB支撑-结构体系的简化力学模型
针对BRB-框架结构体系,通常BRB首先进入屈服状态,因此需要限制BRB的抗侧刚度的大小。若BRB侧向刚度太大,虽然能够增强结构体系的抗侧移水平,但会增大其地震响应;反之,若BRB侧向刚度太小,则达不到地震作用下所需的抗侧移能力。因此,为达到BRB-框架结构体系较好的抗震目标,需要设计BRB-框架结构合理的抗侧刚度比。BRB初始刚度KB计算,需要结合BRB的布置方式确定[6]。结构的抗侧刚度KF用D值法来求解,BRB与结构的抗侧刚度比定义为KD=KB/KF。
分析BRB与结构的不同刚度比KD,如何达到地震作用下BRB-框架结构体系侧移值最小。对于研究某一特定的结构,其结构KF值是一定的,而刚度比值KD同选择的BRB相关,可依靠调整BRB的抗侧刚度来改变KD值,从而实现BRB-框架结构体系的协同工作,减弱结构的地震响应,实现结构的抗震设防目标。
5 实例验算
以文献[7~8]中某L形钢结构工程实例为分析对象。采用MIDAS对L形不规则框架结构进行多遇地震分析,BRB支撑在MIDAS中采用边界条件中的滞后系统来模拟。梁与柱节点为刚性连接,楼板刚性假定,BRB采用倒V形设置,BRB与梁、柱之间连接形式为铰接。

图4 支撑布置
改变BRB与L形钢框架的KD比值,BRB芯材的截面尺寸也随之改变。进行结构抗震动力分析时,首先计算结构的抗侧刚度KF,然后选择抗侧刚度比KD依次为1、2、3、4、5,分别计算出相应的BRB等效截面面积A3,选择合理的支撑截面参数,最后分析不同支撑参数、不同刚度比KD对结构顶层位移、层间位移角等地震响应的影响。
通过合理设置BRB的数量和位置,可以控制不规则结构的扭转,实现结构的耗能减震。在单BRB支撑与同方向总BRB支撑的刚度比一定的情况下,对于L形不规则结构,在结构转角、肢端布置数量一致的BRB(图4),即支撑刚度平均分配,是取得结构抗震效果最有利的方案[9-11]。

表1 模型的前三阶自振周期(S)
地震波采用EL-centro波、Taft波与Lanzhou波3种,通过研究BRB与结构抗侧刚度比KD为1、2、3、4、5的5种支撑方案,得到多遇地震下不同的结构地震响应及控制不规则结构地震效应的结果,因篇幅限制,只列EL-centro波的分析结果(表1和图5~8)。
结构的自振周期体现了结构刚度的改变以及结构对外部因素的响应结果。表1列出了当V支撑与单斜向支撑在刚度比为2时的前3阶周期。

图5 单斜向布置时各方案X、Y方向层间位移角

图6 倒V形布置时各方案X、Y方向层间位移角

图7 单斜向布置时各方案X、Y方向楼层最大剪力

图8 倒V形布置时各方案X、Y方向楼层最大剪力
由表1可看出,BRB布置成单斜向方式和倒V形方式的结构体系自振周期很相近,单斜向布置略大于倒V形,这表明BRB-框架结构体系在BRB单斜向布置时的抗侧刚度同倒V形布置相比略小。
分析图5~6可以得出,对比5种不同的抗侧刚度比方案,当L形不规则框架结构KD在1~5范围内改变时,BRB单斜向布置时X方向最大的弹性层间位移角是1/491,Y方向的最大弹性层间位移角是1/424;BRB倒V形布置时X方向最大的弹性层间位移角是1/563,Y方向最大弹性层间位移角是1/512,5个设计方案都未大于规范1/250的限值。整体分析可得出,KD从1增大5,层间位移角均出现下降的趋势;KD小于2时,框架结构最大弹性层间位移角值是偏大的;KD大于2时,倒V形与单斜向布置相比,有较好的吻合度;但随着KD变大,结构层间位移角下降程度减缓。这表明,仅仅依靠增大BRB支撑面积来降低结构的弹性层间位移角是不可行的。分析图7~8可知,在多遇地震下,此12层不规则框架处在弹性状态,未出现塑性变形;但随着KD的增大,底层剪力出现增大趋势;BRB单斜向布置时最底层剪力的最大值比倒V形大。
6 结论与讨论
通过改变BRB的截面面积,从而实现BRB与结构不同抗侧刚度比KD的要求。对比分析了在不同抗侧刚度比KD,不同BRB布置方式下不规则框架结构的多遇地震响应,可得到以下结论。
(1)随着KD增大,结构的层间位移角均出现减小的趋势,但减小的幅度随之也变缓,通过对比分析,BRB-框架结构的抗侧刚度比KD在2~4范围内是比较合理的。同时分析可知倒V形布置与单斜向相比,有较好的拟合度。
(2)BRB布置成单斜向方式与倒V形方式的结构体系自振周期很相近,且单斜向布置略大于倒V形,这表明BRB-框架结构体系在BRB单斜向布置时的抗侧刚度同倒V形布置相比略小。
(3)增大BRB与结构的抗侧刚度比值KD,则结构的底层剪力也相应地增大。相同KD值情况下,倒V形布置与单斜向比较可更好地减小底层的剪力,削弱结构体系的地震响应,达到结构消能减震的目的。
