基于多尺度样本熵方法分析欧拉视频放大技术在非接触式测量的作用

鲍凯林，陈兆学

上海理工大学医疗器械与食品学院，上海200093

前言

脉搏信号是人体最重要的生理信号之一，它包含大量生理病理信息，体内各种状态变化都会反映在脉搏信号中［1］。而脉搏信号的改变或杂音的出现，往往是人体各器官病症的最早表征。脉搏信号的研究可以清楚地了解身体的生理特性，为疾病诊断提供重要依据。

目前，心电图法是心率测量中应用最广、准确度高的一种方法，但是由于这类接触式测量法中传感器设备需要与人体皮肤接触，造成使用上的不便。由此，非接触式测量方法的优势愈加明显。随着计算机视觉技术的发展，研究人员利用光电容积描记法原理对人体皮肤采集视频进行处理，从而实现对生理信号的非接触测量，该方法也出现相关问题，如不能有效消除噪声、准确度不高等。Poh 等［2-3］和Pursche 等［4］采用独立成分分析算法进行盲源分离处理，对于测量对象人脸中非皮肤区域，发现眼睛眨动对处理结果产生干扰，且噪声频率和心率彼此接近，不易被滤除［5］。另外，盲源分离并没有提供一个判断方法来区分分离后哪一组独立信号更接近于实际心率信号，从而影响到心率的最终计算精度［6］。文献［7］通过脸部跟踪和对脸部变化亮度矫正有效提高算法对移动和环境变化的鲁棒性。文献［8］根据建立皮肤模型和线性盲源分离从脸部多个局部区域提取的体积描记器信号，并使用多数投票法估计心率，进一步提高对被测对象移动和环境亮度变化的鲁棒性，一定程度上克服Li等［9］在复杂测量背景脸部变化亮度矫正可靠性低的不足。2012年，Wu 等［10］提出一种称为欧拉视频放大的方法，来放大视频中物体的微小变化。该方法对时间序列上的每一帧图像中像素点的亮度值进行分析，选择低频部分进行放大，然后与原始图像叠加合成最终图像，从而放大微弱的变化信息。由于不同的变化具有不同的频率，欧拉视频放大技术通过对不同的频率进行分析及放大处理，来实现这些微小变化的可视化。

由于样本熵是一种非线性的分析方法，在整个时间序列中有较好的一致性，不会受数据长度的影响［11］，通过度量信号的复杂度反映它的非线性特征，样本熵值越低，序列的自我相似性越高，序列越简单［12］。本研究利用多尺度样本熵算法［11］对由视频图像得到的脉搏波时间序列信号进行分析，用来衡量相应时间序列在不同尺度上的复杂度基于对其放大前后提取的信号进行时间序列复杂度的计算，对实际处理效果进行比较。

1 欧拉视频放大技术原理

本研究采用欧拉视频放大技术对视频中桡动脉微小跳动进行放大，使视频中脉搏跳动更明显，以便为后续的分析提供重要信息。在视频中，桡动脉处跳动的幅度越大，其位置亮度变化越明显［13］。利用这一特性，可将脉搏的变化由亮度的具体变化来表征。

欧拉影像放大的处理是建立视频帧拉普拉斯金字塔对视频帧空间进行多分辨率分解，对视频帧空间分辨率一样的图像层进行时域处理［14］。欧拉视频放大法是从流体力学的欧拉法角度来研究放大像素值随时间的变化。下面来探究在光流法分析中经常使用的一阶泰勒级数展开法来实现并完成运动放大的。下面仅简单分析进行平移运动的一维信号，由此分析可以推广到二维信号的局部平移运动。用表示图像在空间x处和在时间t处的强度，且用式（1）表示初始时刻：

由于图像中伴随着运动，图像像素值就会随着时间发生变化［15］，若用δ(t) 代表位移函数，即从0 到t时刻x的变化，则在t时刻图像强度可以表示为：

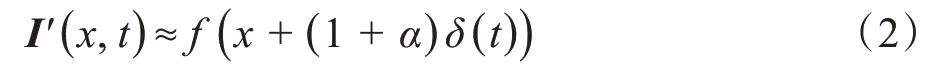
对于此一维信号假设可以用一阶泰勒级数关于x展开，进而得到式（3）：

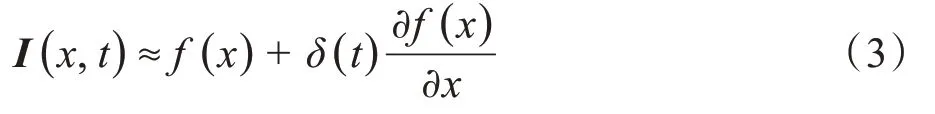
把式（4）表示的带通信号乘以放大因子放大后与原信号相加得到式（5）：

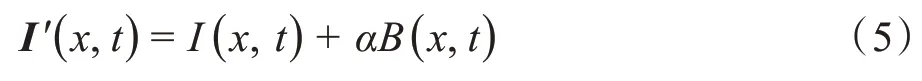
联合式（5）得到式（6）：

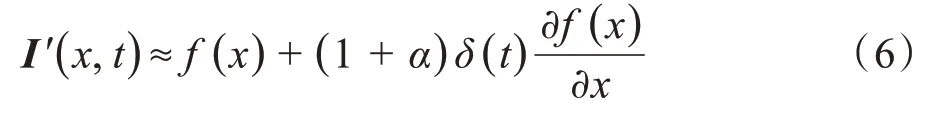
最后再利用一阶泰勒公式得到如式（7）所示的输出信号：

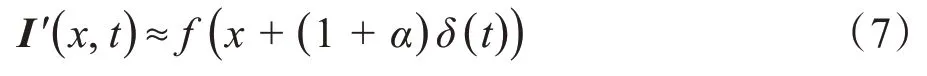
这个过程将图像亮度f(x) 在时间t的位移函数由δ(t)变为( 1 +α)δ(t)。此过程只针对完全在滤波器带宽的视频信号。

为了防止放大失真，对所构造的金字塔中不同空间频率基带应使用合理放大因子进行限制，假设信号空间波长为λ= 2π/ω，其中ω为信号空间频率，则放大因子α限制公式为：

至此，上述过程可实现对于桡动脉跳动部分进行放大的功能，可利用像素点在亮度上的变化情况进行提取生理信号［16］，从而得到相关时频信息。

2 多尺度样本熵计算

样本熵不但具有抗噪、抗干扰的优点，还避免因数据量问题产生的不一致问题［17］，其主要运算思路如下：

（1）假设嵌入维数为m，矢量容量为r，则m维向量可以表示为：

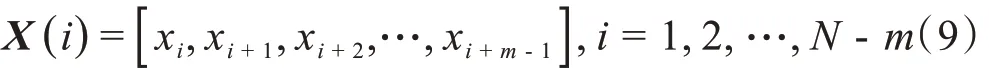
（2）定义x是两者对应时间点差值的最大值，为：

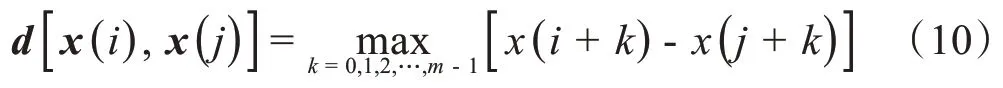
（3）对每个i值，计算x(i)与其余矢量x(j)(j= 1,2,…,N-m;j≠i)间的距离。统计d[x(i),x(j)]小于r的数目以及此值与距离总数N-m- 1的比值，记作(r)，即：

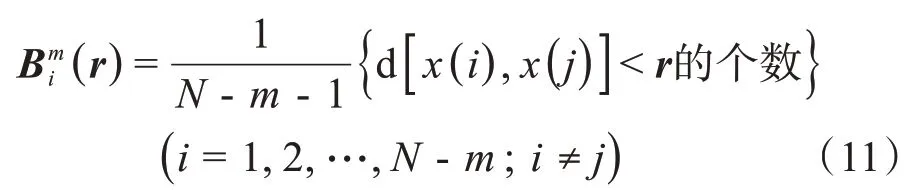
（4）求(r)的平均值：

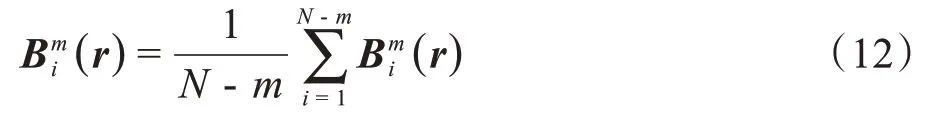
（5）再对维数m+1，即对m+1点矢量重复步骤（1）至步骤（4），得到(r)，进而得到(r)。

（6）理论上此时间序列的多尺度样本熵为：

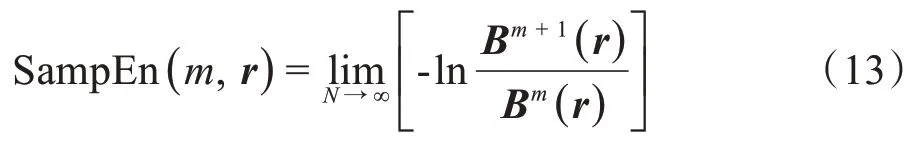
当N为有限数时，式（13）可表示为：

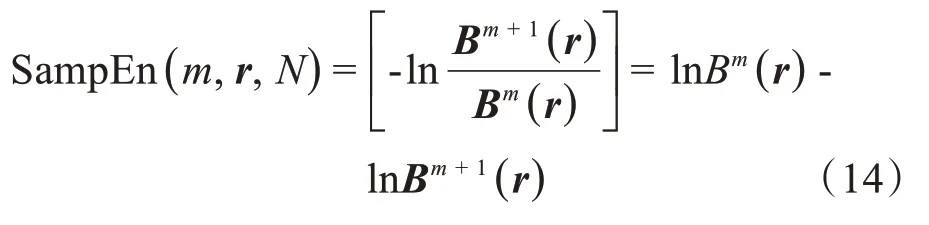
由式（14）可知，SampEn 的值与m、r取值有关。但目前研究还未给出相关明确值。所以，最后计算的SampEn 值就是表征此时间序列复杂度的程度，根据经验［18］，一般取：m=2，r=0.1SD～0.2SD，SD 是原始数据x(i) ,i= 1,2,…,m的标准差。由于多尺度样本熵可以衡量信号的复杂度，样本熵值越低，序列的自我相似性越高，序列越简单。利用这一非线性特性，可用于对其脉搏波信号放大前后的对比，为更精准地对比其时间序列上样本熵的差距，利用瞬时心率的概念进行统计，进行实际效果的比对。

3 试验与分析

3.1 视频数据收集与分析

首先进行视频数据采集，取10位测试志愿者，分成10组，对每组进行非接触式的视频采集，采集部位是桡动脉处，为去除其他无关因素的干扰，所有试验组统一采用苹果手机7 Plus，使其都放置在同一光照下，固定位置拍摄，手臂水平放置在桌面上，位置如图1所示。

图1 视频采集时手臂的位置Fig.1 Position of the arm during video acquisition

欧拉视频放大试验流程：步骤1，视频采集，将10位测试志愿者，分成10组，对每个人进行非接触式的视频采集，为考虑数据一致性，采集部位为左手手腕处，视频时长为15 s，环境为自然光照；步骤2，欧拉视频放大处理，对每个视频进行放大处理，视频时域滤波截止频率为人体的脉搏频率范围：0.3～3.0 Hz；步骤3，ROI的选取，选取桡动脉寸关尺的部位，为避免其他误差的产生，使用同一位置进行ROI的选取，记录其具体的位置信息，使每一位测试者的位置都保持一致；步骤4，生成各通道脉搏波信号，由于彩色视频空间模式为RGB，每个通道产生的信号略有不同，以便后期分析相关性。

本次试验中，为考虑多位测试者的因素，尽量使拍摄位置保持一致。视频的空间信息为RGB，帧率为30 帧/s，拍摄时长为15 s，可获得500 帧左右的图像。如图2所示为未做任何处理的视频截图。

图2 桡动脉处视频截图Fig.2 A screenshot of the video of the radial artery

3.2 多尺度样本熵参数设置

由上述可知，样本熵的值与嵌入维数m、阈值r以及数据长度N有关。3 个参数的选择不同，得到的样本熵结果也随之不同，选取合适的参数尤为重要。由于拍摄视频时，每组视频时长和帧率均相同，所以对应每段视频的图片帧数均为一致，对于数据长度这一项，各试验组没有差别。而嵌入维数m和阈值r需采取控制变量的办法，选取样本熵变化率最小的参数作为结果。

3.2.1 嵌入维数m 的选取这一参数一般取值范围为1～4［14］。本研究采用其中5 位测试者的采集视频，同样经过欧拉视频放大处理后，分别对3通道的视频进行相同的ROI位置的处理，提取脉搏波信号。令阈值r固定（r=0.15Ds），其次分析当m取不同值（m=1,2,3,4）时，样本熵的变化情况，结果如表1所示（其中测试者以A、B、C、D、E代替）。

表1可以看出一些关于样本熵的变化情况，其中变化情况是指数据浮动的范围，以此判断样本熵的稳定程度。经计算，可以看出，在m=2时样本熵的变化最小，这表明其对样本熵的影响最小，所以本研究以m=2为嵌入维数的选择参考值。

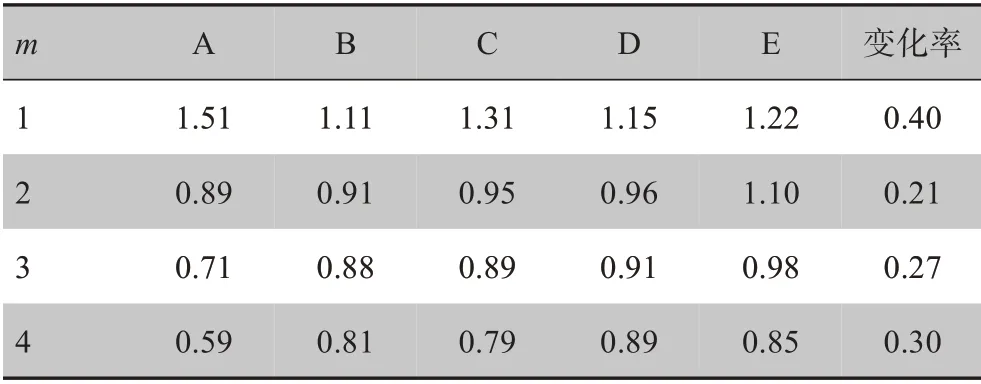
表1 测试者的样本熵（阈值r值固定）Tab.1 Sample entropies of subjects(threshold r remain unchanged)

3.2.2 阈值r 的选取在对于阈值r的选取问题上，r的取值范围一般为0.10Ds～0.25Ds［19］。本次试验中仍以5 位测试者的视频进行验证，令嵌入维数m=2，分析在不同的阈值r（r=0.10Ds、0.15Ds、0.20Ds、0.25Ds）的情况下，整体的样本熵变化情况如表2所示。

表2 测试者样本熵（嵌入维数m值固定）Tab.2 Sample entropies of subjects(the number of embedded dimensions m remained unchanged)

由表2可以看出，当阈值r取0.15Ds时，其样本熵的变化程度最小，所以，在本试验研究的背景下，阈值r取0.15Ds时，整个数据能得到最好的效果。

3.3 多尺度样本熵计算

3.3.1 视频通道的选择为探究在本试验过程中应用哪一通道可得到更好的试验效果，通过计算单一尺度下的样本熵，判断哪个通道可以作为提取信号的通道，依据上述试验过程，其中m=2，r=0.15SD（SD为原始序列的标准差），取10位测试志愿者，分成10组，进行欧拉视频放大，分别计算10位测试者对应放大以后的视频，R、G、B 3个通道，分别计算对应每个视频的R、G、B 3个通道中各自的样本熵值，结果如图3所示。

如图3所示，其中X 轴上1、2、3 分别对应R、G、B 3 个通道，Y 轴表示其样本熵值。共10 组测试者，其中8 组数据在同一视频试验组中都呈现出G 通道的样本熵值最低，表明此通道信号的复杂度较低［13］。在选择通道的问题上可以确定G 通道可作为提取视频信号的通道。

图3 测试者RGB通道样本熵值Fig.3 Sample entropies in RGB channels of subjects

3.3.2 尺度因子的确定由于时间序列复杂度准确性会随着尺度的增加而减小［20］，为确定合适准确的尺度因子，以一组脉搏波信号为例进行试验，试验结果如图4所示，从图中可以看出该试验的样本熵在尺度小于4 的时候，变化情况较为稳定，当尺度从4 到10的时候，样本熵的值增幅较大，不稳定。所以，本试验的尺度因子为1～4较为合理。

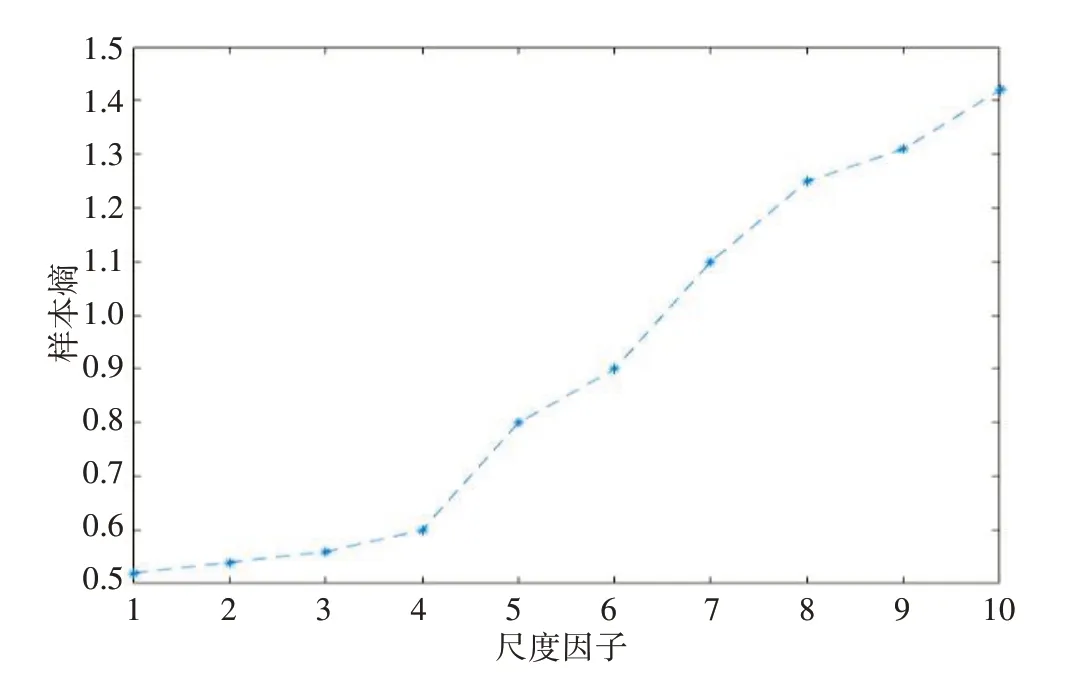
图4 多尺度样本熵分析Fig.4 Multi-scale sample entropy analysis

3.3.3 心率测量比较为进一步验证试验的准确性，考量经过欧拉视频放大技术以后的脉搏信号能否提取到真实的心率信息，其试验结果（图5和图6）与接触式脉搏血氧仪（鱼跃牌电子血压计，符合医药行业标准）同步进行对比分析。取10组测试者，每人进行非接触式和同步接触式心率测量各1次。对其所得脉搏数据采用Bland-Altman法对本试验与脉搏血氧仪进行一致性评估，置信率取95%（1.96标准差），结果如图7所示。

从图7可以看出，对所测数据作符合度分析，标准方差为2.515，95%的置信区间为［-6.5,6.1］，可说明本文心率测量方法与脉搏血氧仪具有较好的一致性。在经过欧拉视频放大技术以后，脉搏信号可提取相应心率的生理参数信息。

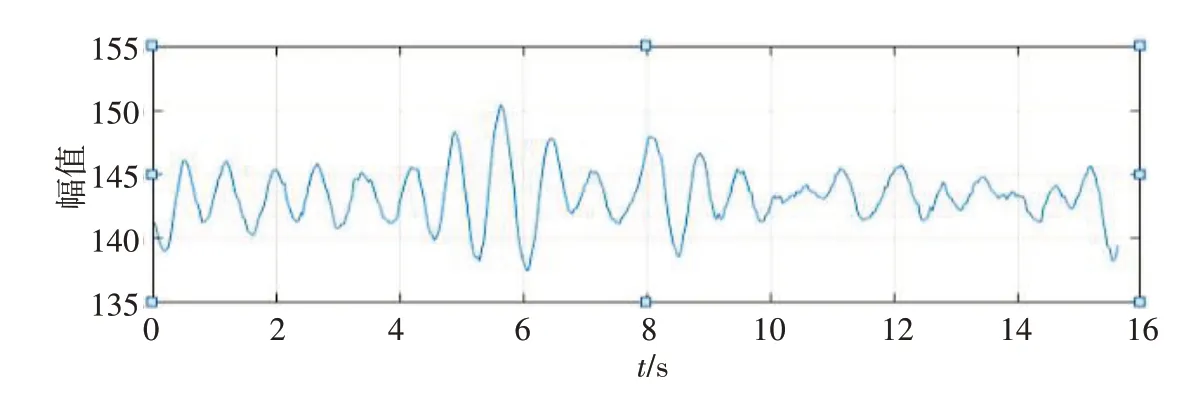
图5 欧拉放大前的脉搏波信号Fig 5 Pulse wave signals before Euler amplification

图6 欧拉放大后的脉搏波信号Fig.6 Pulse wave signals after Euler amplification

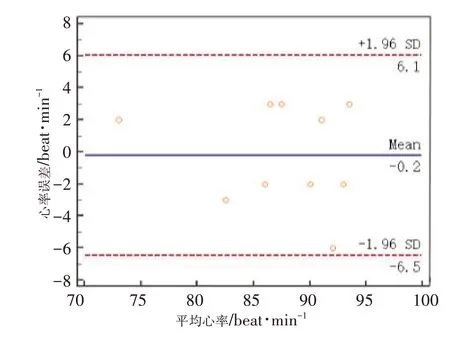
图7 Bland-Altman 法估计两种测量方法结果的一致性Fig.7 Consistency of the results of two measurement methods estimated by Bland-Altman method

3.3.4 放大前后的样本熵比较为了更好地比较欧拉视频放大技术在脉搏波信号分析尤其是动态心率检测中的作用，将信号以波峰的位置为准进行处理，使其分成多个时间间隔，以表示每次搏动的时间间隔，由于在每次搏动中都存在微小变化，用瞬时心率的概念进行检测，即利用每次搏动的时间间隔的倒数表示其瞬时心率，对其进行编码并将每段数值进行样本熵分析，最终进行放大前后效果的比对。使用Matlab 中的findpeaks 函数进行运算，将函数的波峰处进行标记，对每次搏动的时间间隔进行计算并编码。对其进行样本熵计算，由前面试验所知，设置参数阈值r取0.15Ds，嵌入维数m=2，尺度为4。计算结果如图8所示。

图8 放大前后的样本熵Fig.8 Sample entropies before and after amplification

从图8测试结果可以看出脉搏信号放大前后样本熵的变化情况，两者在整体数值上差别不大，整体趋势相似，范围为0.5～0.7，从数值上看，放大后的样本熵数值比放大前略低。图5～图7的试验表明放大前后保持基本脉率，但信号的复杂度有所降低且放大以后更稳定，呈现更为明显的周期性。

3.4 试验分析

上述试验过程主要针对欧拉视频放大技术在比较方面解决两个问题：一个是通过应用样本熵的分析，确定在视频RGB通道中，使用哪个通道能使信号熵值更低，效果更好；另一个是通过样本熵这一数值比较放大前后的信号复杂度。通过以上试验得出以下结论：（1）从图3可以明显看出，在测试的10 位测试者中，在同一个视频中提取的脉搏信号，G 通道的熵值最低，复杂度最低，也是最能表达信号稳定性的状态。（2）在研究脉搏信号的样本熵分析过程中，数据长度在500 的时间序列，适合采用嵌入维数m=2，阈值r=1.5Ds，能取得较好的试验结果。通过将信号利用峰值点分割，计算瞬时心率，分段进行样本熵计算，与放大前的原始信号熵值进行比对，熵值整体差别不大，但经过放大处理后的信号熵值略低。表明经过欧拉视频放大技术前后保持基本脉率，欧拉视频放大技术对数据的复杂度方面有较大的减弱作用，使其信号结果更加稳定。

4 结语

本文研究了基于样本熵的脉搏波信号比较算法，以欧拉视频放大技术为核心，对其实现的原理和方法进行理论定义和描述，从两个方面进行比较，一个是颜色空间通道RGB，比较哪一通道信号的效果最好；另一个是从视频放大前后的角度，比较信号的样本熵变化。通过上述过程，更加深刻地说明了样本熵比较方法对于计算和衡量时间序列复杂度方面的价值。